-
Não entendi. Alguém poderia explicar?
-
55 do primeiro tri, mais 48 do segundo. Total 103. Logo, pelo menos 3 são repetidos.
-
Você tem 55 em recuperação no 1º, ou seja, 45 aprovados.
Quando você vai analisar os 48 em recuperação no 2º, suponha que entre eles, estão os 45 aprovados no 1º (ainda vão faltar 3 para fechar os 48). Portanto, obrigatoriamente, no mínimo esses 3 também ficaram em recuperação no 1º.
-
e o terceiro tri, ninguem conta?
-
Ainda não intendi bem a resolução. Alguém sabe de algum vídeo que explica melhor essa questão?
-
Tava tentando resolver pelo diagrama de Venn... quebrei a cabeça e não enxerguei essa solução simples...
Mas pergunto, o diagrama de Venn também poderia ser usado pra resolver? Como ficaria?
Obrigado
-
Saudações!
A resolução neste link está bem didática: http://www.youtube.com/watch?v=PGYDViDqoCc
Abraço e bons estudos!
-
O que eu não compreendo e que não vi ninguém considerar é que dentro do grupo dos aprovados e reprovados podem haver alunos comuns. Por exemplo, os 48 alunos em recuperação no segundo semestre poderiam estar dentro do grupo dos 55 alunos em recuperação no primeiro trimestre... O problema não fala que eles, necessariamente, fazem parte de grupos separados... Dessa forma a resolução do problema mudaria.. ME CORRIJAM SE EU ESTIVER ERRADO...
-
Resolução completa da prova de raciocínio lógico: https://www.youtube.com/watch?v=K5MbJrWPpCs
-
questão mega mal elaborada. Pois a letra C também poderia ser considerada correta, pois a questão não valida corretamente os dados informados. Ora, no 2º T ficaram 48 alunos em recuperação ou seja está contido ai 40 alunos; no 3º T ficaram os exatos 40 alunos que a alternativa colocou já está correta a primeira parte da alternativa e os demais alunos ficaram em recuperação no 1 º T.
Parece as questõezinhas elaborada pela CESPE.
-
Não está mal formulada. a alternativa C diz " 40 ficaram em um semestre - essa parte está correta - e os demais em um único semestre - errado, pois conforme os colegas já demonstraram, 3 colegas ficaram em recuperação no primeiro e no segundo semestres.
correta alternativa A
-
Caro Colega Leandro, a sua dúvida procede, porém vc está considerando apenas um dos extremos, ou seja, na hipótese de todos aqueles alunos que ficaram para recuperação no 1º trimestre, vierem a ficar também no 2º trimestre.Pense, agora, no outro extremo, ou seja, na hipótese de nenhum dos alunos que ficaram para recuperação no 1º trimestre vierem a ficar no 2º (ou seja, ficaram para recuperação no 2º trimestre todos os 45 alunos que foram aprovados no 1º trimestre). O que vai acontecer? Como foram “45”, então vão estar faltando “3”, haja vista,no 2º trimestre, “48” alunos ficaram para recuperação. Dessa forma, conclui-se que, necessariamente, no mínimo 3 alunos ficaram para recuperação em ambos os dois primeiros trimestres. Vamos em frente que atrás vem gente!
-
Questão bem simples pessoal. Façam o seguinte (pelo menos dá certo comigo): cometam um erro. Calma. O que a letra "A" nos diz é que existe uma intersecção entre o "1º Semestre" e o "2º Semestre", então somemos os 2 conjuntos e obteremos 103, ou seja, superamos em 3 o universo (a escola) em que há apenas 100. Portanto, a resposta é letra "A".
-
Vamos
tentar provar a autenticidade de cada alternativa utilizando diagramas, assim:
A)
Fazendo o diagrama:

B)
Montando um contra exemplo abaixo, de acordo com os dados do problema:
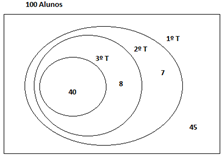
Logo, percebe-se
que nem todos os alunos ficaram em recuperação. Alternativa errada.
C) Utilizando o mesmo diagrama montado acima
como um contra exemplo, podemos concluir que a alternativa está incorreta.
D) Vamos
construir um contra exemplo para invalidar a alternativa:
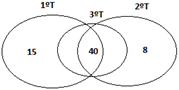
Assim,
encontramos nesse contra exemplo, onde se tem duas situações onde alunos se
encontram em recuperação em um único semestre e uma situação onde alunos se
encontram em recuperação nos três semestres ao mesmo tempo, mas nenhum em 2
semestres simultaneamente.
Logo
a alternativa está errada.
E)
Na situação 1 abaixo, conseguimos montar um contra exemplo que contraria a
primeira afirmação da alternativa.
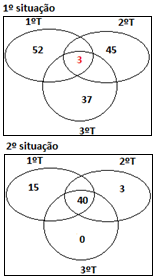
Logo a alternativa E está errada.
-
soma-se 55+48=103
entao 3 alunos ficaram em recuperaçao no primeiro e tambem no 2
-
mas pessoal, se nao houvesse as opções de respostas seria impossivel descobrir todos os elementos pertencentes aos trimestres?
nao existe uma formula pra resolver, sem ser por eliminação de respostas?
-
Aplicação do chamado "princípio da casa de pombos".
-
-
Questão difícil. Mas veja só, se no primeiro trimestre 55 ficaram de recuperação, significa que 45 passaram.
No segundo trimestre, 48 ficaram de recuperação, ou seja, 45 passaram e mais 3 ficaram de recuperação, esses 3 só podem ser os mesmos que ficaram no primeiro trimestre. Errei a questão, mas achei esse raciocínio mais simples que os dos colegas.
-
Mesmo com o vídeo do Joselias , tá puxaado!
-
55 + 48 = 103 (sabendo que a classe possui 100 alunos, pelo menos 3 alunos ficaram em recuperação no 1º e também no 2º trimestre.)
GABARITO ''A''
-
Alunos = 100
55 alunos recuperação 1º trimestre
48 alunos recuperação 2º trimestre
40 alunos recuperação 3º trimestre
100 - 55 = 45 (aprovados)
100 - 48 = 52 (aprovados)
100 - 40 = 60 (aprovados)
Soma-se o 1º trimestre com o 2º trimestre, já que se somarmos qualquer um dos dois com o 3º trimestre o nº de aprovados irá ultrapassar o nº de alunos da escola.
45 + 52 = 97 (aprovados direto)
100 - 97 = 3 (alunos em recuperação nos 1º e 2º trimetres)
-
eu fiz pelo diagrama.
100 - 143 ( soma dos 3 trimestres) = 43 (intersecção)
1 trimestre : 55 - 43 = 12
2 trimestre : 48 - 43 = 5
3 trimestre: 43 - 40 = 3
12 + 5+ 3 +43 = 63 alunos em recuperação
100 - 63 = 37 alunos passaram direto, com isso já eliminariamos a letra B e E, a letra C também não poderia ser, porque na intersecção deu 43, a letra D não se pode ter certeza, já que com os dados achamos apenas a intersecção dos 3, a letra A é a única cabível.
-
caindo isso na cespe, deixa em branco e parte pra próxima que vc ganha mais tempo e nao arrisca errar
-
https://www.youtube.com/watch?v=K5MbJrWPpCs
Daniel Dudan é infinitamente mais prático que o professor Josélia do outro video sugerido .
-
Questão mal elaboraada SIMM! O mais engraçado são os os professores querendo concordar com a banca de todos os jeitos!! Questão carregada de subjetividade. Veja que existe possibilidade de eu provar que a alternativa'' A está ERRADA'' Imagine que 63 alunos nao ficaram em recuperação em nenhum dos trimetres. Somente no primeiro = 15. somente no segundo = 8. Somente no terceiro = 0. Primeiro e segundo = 0. Primeiro e terceiro = 0. Segundo e terceiro = O. Primeiro, segundo e terceiro = 40. Façam o diagrama e veja que existe esta possibilidade e nao dá pra afirmar necessarimente como diz a questão. 15+ 40+ +8 + 63 ( de fora do diagrama) = 100. TRISTE FCC!!!
-
Comentário do Alexandre/SG está ok. Bom para entender!
-
Ahhh!!!Pelo amor de Deus!!!! Que questão é essa???
-
RESPOSTA DO ALEXANDRE É A MELHOR.
-
Achei a resolução do professor do QC difícil. OS comentários aqui estão melhores. Imagina perder tempo fazendo os diagramas.
-
Igor Figueiredo matou a questão simples e rápido. Show de bola, 10 likes pra você amigo. Apesar de terem várias respostas ótimas dos demais colegas. Essa foi direto ao ponto.
-
BIZARRICE... PERCA 15 MINUTOS DA SUA PROVA RESOLVENDO ISSO E ESTARÁ ACABADO NO CONCURSO... SEMPRE ODIEI MATEMÁTICA, Ô INFERNO!
-
https://youtu.be/P4ZEKcbPtdI
-
Vejamos cada afirmação:
(A) todos os alunos da escola ficaram em recuperação em, pelo menos, um trimestre. ERRADO.
Pode haver repetição, entre os alunos que ficaram de recuperação em cada trimestre.
(B) 40 alunos ficaram em recuperação em dois trimestres e os demais em um único. ERRADO.
Não podemos inferir isso das informações fornecidas.
(C) Pelo menos um aluno da escola ficou em recuperação em somente dois trimestres. ERRADO.
Ex.: Imagine que os 40 alunos que ficaram de recuperação no 3o trimestre também ficaram no 2o e no 1o . Assim, dos demais 60 alunos, pode ser que 15 tenham ficado de recuperação somente no 1o trimestre (totalizando 55), e que outros 8 alunos tenham ficado de recuperação somente no 2o trimestre (totalizando 48). Neste caso, que é possÌvel, 40 alunos teriam ficado de recuperação nos 3 trimestres, outros 15 + 8 = 23 teriam ficado de recuperação em apenas 1 trimestre, e NENHUM aluno teria ficado de recuperação em somente dois trimestres.
(D) No mínimo 5 e no máximo 40 alunos ficaram em recuperação nos três trimestres. De fato o máximo de alunos que podem ter ficado de recuperação nos 3 trimestres é 40, pois este é o máximo que temos no 3o trimestre. Já para obter o mínimo, sabendo que 55 ficaram de recuperação no 1 o trimestre, vamos imaginar que os 45 restantes tenham ficado de recuperação no 2o trimestre. Como ao todo foram 48 os que ficaram de recuperação no 2o trimestre, é preciso “emprestar” mais 3 alunos dos 55 que ficaram no 1o trimestre, de modo que esses 3 alunos ficaram de recuperação no 1o e no 2o trimestre. Agora suponha que 40 dos 55 alunos que ficaram de recuperação no 2o trimestre (e não ficaram no 1o) tenham ficado de recuperação também no 3o trimestre. Neste caso, ficamos com 3 alunos que ficaram de recuperação no 1o e 2o trimestre, e 40 alunos que ficaram de recuperação no 2o e 3o trimestres, e NENHUM aluno que ficou de recuperação nos 3 trimestres. Ou seja, é possÌvel que no mÌnimo 0 (nenhum) aluno tenha ficado de recuperação nos 3 trimestres. ERRADO.
(E) Pelo menos 3 alunos ficaram em recuperação no 1o e também no 2o trimestre .CORRETO.
Quando separamos 55 alunos para ficar de recuperação no 1o trimestre, sobram apenas 45 para ficarem de recuperação no 2o trimestre. Como foram 48, é preciso “emprestar” pelo menos 3 alunos dentre aqueles que ficaram de recuperação no 1o trimestre.
Resposta: A
FONTE: ESTRATÉGIA CONCURSOS