-
De acordo com o enunciado, temos aqui
“n" executivos apertando a mão uma única vez de outros.
Logo, se caracteriza uma
combinação de “n" pessoas que apertaram a mão tomados 2 a 2, resultando no
total de 78 apertos, assim:
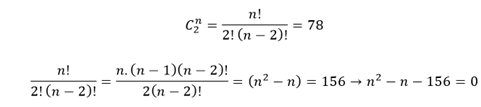
Resolvendo a equação de
segundo grau, encontraremos as raízes n = -12 e n = 13. Como não queremos
valores negativos para “n", a resposta que procuramos então é n = 13.
RESPOSTA: CERTO
-
Uma forma prática de resolver esta questão é usar a resposta como teste.
C(15,2) = 105 apertos de mãosC(13,2) = 78 apertos de mãosNote que trata-se de uma combinação e para haver o cumprimento deve-se formar sempre duplas.Logo, item Certo.
-
Para que se tenham 78 apertos de mão a ordem das pessoas que se dão às mãos não faz diferença no resultado e com isso tem-se uma combinação, daí calculando fica:
Cn,2 = 78
Com isso teremos:
n!/2! = 78
Desenvolvendo vamos obter:
n.(n-1)/2 = 78
n² - n = 78
n² - n - 78 (equação do 2º grau)
Com isso vamos obter duas raízes, uma positiva e outra negativa, com valores -12 e 13. Como não podemos obter como resposta um valor negativo teremos como gabarito o valor 13, portanto a assertiva está correta.
FORÇA E HONRA.
-
Método infálivel para qualquer questão neste mesmo cenário:
x (x - 1) = 78
2
x (x - 1) = 156
x² - x - 156 = 0 Equação do 2º grau
Fazendo via Bhaskara
x = 13
Gab: Correto
-
acertei usando uma conta tão bizarra que é melhor nem comentar kkkk
-
Vou escrever em Português, pq vejo gente explicando em Alemão.
Comecei a divisão pelos números pares 2,4, 6: 78:6= 13. Logo, tínhamos pessoas presentes.
-
Eu fiz de umm jeito tão errado, mas, sei lá, na minha cabeça fazia sentido. Se tem 10 pessoas numa sala, eu incluso, aí eu vou apertar 9 mãos. Cada uma das pessoas irá apertar 9 mãos, e já daria mais de 78, então seriam menos.
Depois eu vejo que eram 13 pessoas, aí não entendi mais nada
-
Gente, não precisa fazer todo esse cálculo. Se tiverem 15 pessoas, a primeira pessoa vai cumprimentar 14, a segunda 13, a terceira 12, ou seja, a resposta é 14!.
Começando de 14 + 13+12 ... logo percebe que vai passar de 78, então só pode ser menos do que 15 pessoas.
-
É possível fazer sem decorar fórmula
2 1
3 (+2)3
4 (+3)6
5 (+4)10
6 (+5)15
7 (+6)21
8 (+7)28
9 (+8)36
10 (+9)45
11 (+10)55
12 (+11)66
13 (+12)78 //
13<15
GABARITO CORRETO