-
Para atender a condição de que terminem simultaneamente, resposta é obtida calculando o MDC entre 500,300 e 150 que corresponderá ao maior número inteiro capaz de dividir as três quantidades de forma a obter resultados inteiros. o MDC= 50. Feito isto, Para que cada tarefa termine em exatos 50 dias, uma certa quantidade de tarefas diárias deverá ser realizada conforme o número de cada tarefa. TA: 500/a=50; TB: 150/b=50; TC: 300/c=50. Sendo a, b, c o número de tarefas de cada tipo realizadas por dia. a+b+c=19, "Aternativa D"
Ocorre que a questão foi mal formulada pois define um critério que não pode ser atendido pelas alternativas. reproduzindo o texto:
"...sendo necessário finalizar as tarefas dos tipos A, B, e C simultaneamente ao final do último dia. De acordo com as instruções que recebeu, ele tem que realizar, por dia, sempre o mesmo número de tarefas A, o mesmo número de tarefas B e o mesmo número de tarefas C, sendo que a soma diária da quantidade de tarefas A, B e C realizadas seja a maior possível.
O único critério relacionado ao número de dias é que seja o mesmo para as tarefas A,B,C.
Quanto ao número de tarefas executadas existem 2 critérios:
I. cada tarefa deve ser executada por igual a cada dia, ou seja as quantidades diárias devem ser as mesmas a cada dia.
II. A SOMA TOTAL DE TAREFAS DIÁRIAS DEVE SER A MAIOR POSSÍVEL. É esse critério que o gabarito não atende. O MDC indica o maior divisor comum entre 500, 150 e 300. Isto determina o maior tempo possível para execução das tarefas e consequentemente a menor quantidade possível de tarefas diárias.
Na realidade a maior soma de tarefas diárias seria: 950 tarefas em um único dia. Sendo 1 o menor divisor comum. Como a questão fala que o funcionário tem alguns dias, descartamos esta hipótese. O divisor imediatamente maior seria o 5. Em 5 dias seriam realizadas 100 TAs, 30TBs e 60 TCs = 190 Tarefas a cada dia, o que resultaria em uma soma "MAIOR POSSÍVEL" de tarefas diárias
Caso fossem feitas em 25 dias, a soma diária também seria maior que o gabarito . Minha conclusão é que a questão deveria restringir o critério, combinando o maior soma diária de tarefas no maior tempo possível, então a resposta "19" satisfaria a questão.
Usando 1, 5, 25 e 50 dias, teríamos uma soma diária constante de tarefas = 950>190>38>19. Ou seja, 19 é a menor soma possível de tarefas diárias.
"ai... que burro, dá zero pra ele."
-
Questao '' quase classica '' de MDC.
Solucao:
Como o total de cada tarefa deve ser o mesmo, temos o primeiro criterio para o MDC: o divisor para cada tarefa deve ser COMUN.
Alem disso, a soma diaria deve ser a maior possivel, logo, temos o segundo criterio: o divisor deve ser o MAXIMO possivel.
Dessa forma, temos que fazer a decomposicao em fatores primos das tarefas A, B e C. Assim:
A= 2^2 x 5^3
B= 2x3x5^2
C= 2^2x3x5^2
Para o MDC tomamos APENAS os fatores comuns e com MENORES espoentes. Logo:
MDC( 500,150,300)= 2x5^2= 50
Entao, diariamente, ele executara , para cada tarefa, o total de :
A=> 500/50=10
B=> 150/50= 3
C=> 300/50= 6
Portanto, por dia , executara:
10+3+6= 19 tarefas
Letra: D
-
Concordo com o Rafael Alencar. A maior soma é 950 em 1 dia. Em dois dias dava para fazer 475. Certamente o enunciado está incompleto. Demorei a chegar a uma conclusão. Na intuição fui decompondo e cheguei ao 19. Não sabia se estava certo, foi mais na sorte.
-
Alternativa: D
A = 500 tarefas; B = 150 tarefas; C = 300 tarefas.
Total geral de tarefas = 950
A=500/950 simplificando a fração =>10/19 |
B=150/950 simplificando a fração => 3/19 | Ele terá que fazer por dia: 10 tarefas tipo A, 3 tarefas tipo B e 6 tarefas tipo C
C=300/950 simplificando a fração => 6/19 |
Obs: ele precisará de 50 dias para concluir todas as tarefas nessas condições.
-
Bom, sinceramente, concordando com os colegas, esse enunciado em minha opinião está falho. Ele não deveria apontar o MÁXIMO de tarefas ao dia, ele deveria pedir as tarefas no MÁXIMO NÚMERO DE DIAS. Afinal, conforme as opções do gabarito, certamente essa é uma questão clássica de MDC. Logo, se ele pedir o máximo de tarefas ao dia, o candidato não tem qualquer óbice em considerar que poderão ser realizadas em um dia, em dois dias, em 5 dias, etc..o que torna a questão sem um ponto de referência correto que não seja o gabarito, obrigando o candidato a "adivinhar" qual a melhor resposta...Questão péssima...capricha mais FCC!!
-
Gente, bateu uma dúvida aqui. Achei 15...
-
150 300 500 2
75 150 250 5
15 30 50 5
3 6 10 50
Fazer o MDC de 150, 300 e 500 - como foi feito acima, dá 2, 5, 5 = que multiplicando dá 50 - ou seja, ele vai levar 50 dias.
O que sobra, simplesmente sobra, pq no MDC não se tenta fatorar mais quando não há mais um múltiplo comum. E essa sobra será o número de tarefas que ele vai fazer, por dia, de cada um dos tipos (A, B, C) - que somados (3 + 6 + 10) = 19.
Pra tirar a prova, basta dividir 950 por 19 que dará os 50 dias.
-
Aonde consta no enunciado da questão que as tarefas devem ser concluídas no maior tempo possível?
Para exemplificar, ele poderia concluir a tarefa em 10 dias, concluindo em cada dia 50 tarefas do tipo A, 15 tarefas do tipo B e 30 tarefas do tipo C. Ainda assim, não se estaria transgredindo nenhuma informação trazida pela questão.
-
Ainda que a questão envolva o MDC, o enunciado exige:
a) que as tarefas sejam concluídas ao mesmo tempo.
b) que a cada dia sejam feitas o mesmo número de tarefas A, B e C.
c) que a soma diária da quantidade de tarefas seja a maior possível.
O resultado de 19 já foi encontrado pelos colegas.
A questão, porém, pede que seja realizado maior número de tarefas possíveis ao dia. Para que se mantenha a proporcionalidade diária ao longo do período (não estipulado), o MDC seria o máximo de tarefas de A que ele poderia realizar em um único dia, ou seja, 50 tarefas "A" (acima disso perde-se a proporcionalidade e abaixo perde-se a eficiência máxima exigida). Logo, seria necessário, no mínimo, 10 dias para a conclusão das tarefas "A" (500/50), sendo as demais adequadas proporcionalmente ao longo desses dias.
Tendo em vista que ele precisa concluí-las ao mesmo tempo, deveria, pois, se dividir todas as tarefas B e C ao longo desse período.
Sendo assim:
Prazo: 10 dias.
A = 500/10 = 50
B = 150/10 = 15
C = 300/10 = 30
Logo, para que a quantidade de tarefas seja a MAIOR POSSÍVEL AO DIA e IDÊNTICA/PROPORCIONAL em todos os dias do prazo, o prazo deveria ser 10 dias e o número de tarefas máxima ao dia totalizaria 95.
Questão muito mal formulada.
-
"..De acordo com as instruções que recebeu, ele tem que realizar, por dia, sempre o mesmo número de tarefas A, o mesmo número de tarefas B e o mesmo número de tarefas C, sendo que a soma diária da quantidade de tarefas A, B e C realizadas seja a maior possível..."
Yuri, num primeiro momento eu também achei que a banca estava afirmando que a quantidade de tarefas A, B e C, realizadas diariamente fosse o mesmo número (A=B=C). No entanto, me dei conta de que a banca queria apenas que os RESPECTIVOS números de tarefas A, B e C, realizadas diariamente, fossem os mesmos, ou seja, não variassem ao longo dos dias, podendo sim ser números diferentes entre si.
-
fazer o MDC e depois regra de três simples
-
Encontrando o MDC de 150, 300 e 500:
Fatorando o número 150 temos:
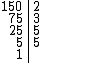
Logo: 150 = 2 . 3 . 52
Fatorando o número 300 temos:
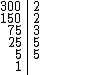
Logo: 300 = 22 . 3 . 52
Fatorando o número 500 temos:
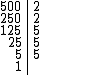
Logo: 500 = 22 . 53
Levando-se em conta os fatores comuns e não comuns, com os maiores expoentes temos que:
MMC(150, 300, 500) = 22 . 3 . 53 = 1500
Considerando-se os fatores comuns com os menores expoentes temos que:
MDC(150, 300, 500) = 2 . 52 = 50 dias
Então, diariamente, ele executará , para cada tarefa, o total de :
A → 500/50=10
B → 150/50= 3
C → 300/50= 6
Então, por dia será executado:
10 + 3 + 6 = 19 tarefas
Resposta: Alternativa D.
-
Pra que a soma de tarefas seja a maior possível, nós teríamos que ter a maior quantidade de tarefas por dia, logo, teríamos 10 dias de tarefa nos quais utilizaríamos 50 tarefas, 15 tarefas e 30 tarefas por dia.... Ou seja, não haveria sequer alternativa adequada.
Acertei a questão porque presumi que ele QUERIA dizer outra coisa, mas... O enunciado está mal elaborado. Nao tem como negar.
-
Como eu fiz:
Tirei o MDC dos três que deu 50:
500, 150, 300 | 2 , 5, 5 (2x5x5 = 50)
250, 75, 150
50, 15, 30
Depois dividi o resultado do MDC por cada um:
500/50 = 10
150/50 = 3
300/50 = 6
Somei os três e encontrei 19.
-
Para solucionar essa questão basta trabalhar com os números de tarefas e
depois encontrar os valores para somar a quantia de tarefas diárias. Não é necessário encontrar a quantidade de dias.
Tirei o MMC dos valores apresentados no enunciado:
500,150,300 I 10 (dividi logo por 10 pra reduzir o possível)
50, 15, 30 I 5
10, 3, 6 esses valores correspondem as tarefas dos tipos A, B e C. Então: 10+3+6=19 (alternativa d)
Bons estudos!
-
ORIENTAÇÃO: simplificar enquanto houver divisor comum aos 3 números.
..A.........B........C
.500.....150.....300...................(divide por 10)
.50........15.......30....................(divide por 5)
.10.........3..........6
CONCLUSÃO 1: se multiplicar os divisores (10 e 5), teremos o números de dias para concluir a tarefa (50 dias)
CONCLUSÃO 2: os restos das divisões correspondem ao número de tarefas a serem realizadas por dia.
Logo,
tarefa A= 10 por dia,
tarefa B= 3 por dia.
tarefa C= 6 por dia.
Assim, o total de tarefas por dia (A + B + C) é 19.
-
Veja que é preciso realizar a cada dia o mesmo número de tarefas A, o mesmo de B, e o mesmo de C, e devem ser realizadas o máximo de tarefas possíveis por dia. Como temos números diferentes de tarefas (500, 150 e 300), devemos buscar o máximo divisor comum (MDC) entre esses números, que é 50. Assim, a cada dia realizaremos 500/50 = 10 tarefas A, 150/50 = 3 tarefas B, e 300/50 = 6 tarefas C, totalizando 10 + 3 + 6 = 19 tarefas por dia.