-
X = empresas que encerraram as atividades este ano
Y = empresas que foram abertas em anos anteriores
X ∩ Y = 1/9 das que encerraram as atividades este ano foram abertas em anos
anteriores, 1/10 das que foram abertas em anos anteriores encerraram as atividades este ano
Ou seja:
1/9 de X foram abertas em outros anos
1/10 de Y encerraram suas atividades este ano
Portanto,x/9 = y/10
x = 9y/10
O total é igual a 2.000, então somando as que apenas encerraram este ano + as que abriram em
outros anos + as que estão nos dois conjuntos + as que não estão em nenhum, teremos um valor
de 2000. Matematicamente:
8x/9 + 1x/9 + 9y/10 + 200 = 2000
Vamos substituir o Y por 10x/9, já que Y = 10x/9:
9x/9 + 9/10 *10x/9 = 2.000 – 200 (9x/9 = 1x) (simplifico 9 com 9 e o 10 com 10, sobra X)
X + X = 1.800
2x=1800 x = 900
Y = 10x/9
Y = 10/9 * 900
Y = 9000/9 = 1.000
Agora podemos resolver a questão
Sabemos que y = 1.000 e X = 900, então: 1.000 > 900 ???? CERTO!
PS: Como faço para adicionar imagem no comentário? com a imagem seria mais simples de explicar!
-
Sem contas é melhor. Coloca qualquer numero na intercessão. Arma o problema. Substitui esse número. Veja se em A ou B ficou maior... sacou?
-
Pessoal a questão é mais de interpretação! Pois os valores calculados devem ser "trocados"
Observe:
1/9 das empresas que encerraram as atividades esse ano FORAM ABERTAS EM ANOS ANTERIORES, Logo 1/9 de 1800 = 200
Logo 200 empresas foram abertas em anos anteriores
Obs: 1800 porque é 200 menos 200 que não estão em nenhum desses grupos!
1/10 das empresas que foram abertas em anos anteriores ENCERRARAM AS ATIVIDADES ESSE ANO, 1/10 de 1800 = 180
(encerraram as atividades esse ano) 180 < 200 (foram abertas em anos anteriores)
Firme e Forte
1800 porque é 200 menos 200 que não estão em nenhum desses grupos!
-
Dizer que
(1) x empresas encerraram atividade em 2014 (por exemplo) e foram abertas antes de 2014
é a mesma coisa que dizer que
(2) x empresas foram abertas antes de 2014 e encerraram a sua atividade em 2014.
Ou seja, o número de empresas (X) será o mesmo.
Se eu divido um número y por 9 para dar x e depois divido um número w por 10 para dar também x, obviamente que, se eu estou dividindo por um número maior para ter o mesmo resultado, o número w tem que ser maior do y.
Logo, o número de empresas abertas antes de 2014 (w) é maior do que o número de empresas que encerraram a atividade em 2014 (y).
-
200 = empresas que não encerraram as atividades este ano e não foram abertas em anos anteriores
X = empresas que encerraram as atividades este ano, mas não foram abertas em anos anteriores
Y = empresas que foram abertas em anos anteriores, mas não encerraram as atividades este ano
X/9 = Y/10 = empresas que encerraram as atividades este ano e foram abertas em anos anteriores
X = 9/10 Y
(9/10 Y) + (Y/10) + Y = 2000 - 200
2Y = 1800
Y = 900
X = 9/10 Y = (900 * 9)/10
X = 810
Logo Y > X => CERTO
-
Danilo Capistrano é só você inserir aqui o link da imagem que você quer exibir. Já vi outras pessoas fazerem isso, acho que é a única forma de inserir imagem.
-
Que enunciado confuso :/
-
Pra quem está precisando de uma explicação em vídeo: https://goo.gl/yeZ1Ds
A resolução começa em 00:53
Abraço
-
ai gente! queimei os fusíveis...
bom, eu achei o resultado usando o seguinte raciocínio:
são 2.000 empresas
200 estão fora, pois nem abriram e nem fecharam.
sobram 1800
A-----1/9 de 1.800 é 200 , então, 200 das que encerraram as atividades este ano foram abertas em anos anteriores.
B-----1/10 de 1,800 é 180, então, 180 que foram abertas em anos anteriores encerraram as atividades este ano.
agora é só comparar A e B
-
X sao as empresas que fecharam Esse ano.
1/9 de X foram criadas em anos anteriores
E das que foram criadas em anos anteriores, 1/10 fecharam esse ano, ou seja,
(1/9X) x 1/10, logo, as que foram criadas em anos anteriores, 1/9X é maior do que 1/9X x 1/10.
-
Vão direto ao comentário mais votado, Danilo , a resolução dele é a correta.
-
Correta Questão:
Total de empresas: 2.000 / Empresas NÃO, Fechadas/Abertas 200
2.000 - 200 = 1800
Fazemos o seguinte cálculo:
1
- = 222
9
1
- = 200
10
Temos a seguinte fórmula: 222-x+x-x200= 1800
Logo: -x = 422 - 1800 = x= 1382 Obs: Temos a interseção.
Empresas fechadas= 1160
Empresas abertas= 1182
O número de empresas que foram abertas em anos anteriores é superior ao número de empresas que encerraram as atividades este ano.
Se possível, é necessário fazer o gráfico para tira dúvidas que possa surgi.
Bons estudos.
-
Pessoal, foram 1800 empresas que encerraram as atividades no ano corrente.
Se 1/9 das empresas que encerram atividades neste ano é que foram abertas em anos anteriores então são 200 empresas.
Se 1/10 das empresas foram abertas em anos anteriores encerraram suas atividades este ano, ou seja 200. Então o total de empresas que foram abertas no ano passado é 2000 que é a soma das que não encerraram as atividades este ano e as que encerram as atividades este ano(200). Sabendo que as que encerraram as atividades este ano é 1/10 ou seja 10% então o total é 2000.
Respondendo
O número de empresas que foram abertas em anos anteriores (2000) é superior ao
número de empresas que encerraram as atividades este ano (1800).
Certo
-
Resolução do professor Helder Monteiro
https://www.youtube.com/watch?v=gMHIFnZy0z0
-
Sabemos que em um grupo de 2.000 empresas, 1/9 das que encerraram as atividades este ano foram abertas em anos anteriores e que 1/10 das que foram abertas em anos anteriores encerraram as atividades este ano, ou seja, 1/9 das que encerraram as atividades este ano (X) é igual a 1/10 das que foram abertas em anos anteriores (Y), que, no diagrama, seria a interseção dos conjuntos.
Do total de 2.000 empresas, 200 não fazem parte nem de X, nem de Y, ou seja:
i) 1 - 1/9 = 8x/9 (complemento de 1/9) seriam as que somente encerraram este ano.
ii) 1 - 1/10 = 9y/10 (complemento de 1/10) seriam as que foram abertas em anos anteriores.
E concluindo, x/9 ou y/10 a interseção dos conjuntos X e Y.
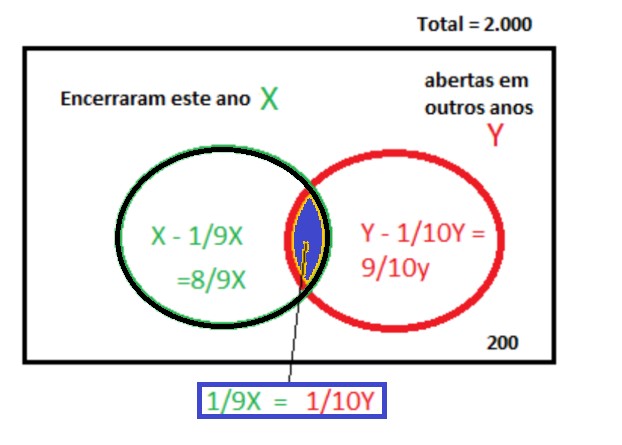
Logo, montando um sistema de equações:
| x/9 = y/10 → y = 10x/9 (I)
| 200 + 9y/10 + 8x/9 + x/9 = 2000 (II)
Substituindo I em II:
200 + 9*(10x/9)/10 + x = 2000
200 + (90x/9)/10 + x = 2000
10x/10 + x = 1800
x = 900.
Substituindo em I:
y = 10*900/9
y = 1000.
Assim, 900 em empresas encerraram as atividades este ano e 1000 foram abertas em anos anteriores.
Resposta: Certo.
-
Qconcursos, se tem uma matéria que seria interessante disponibilizar os comentários do professor EM VÍDEO, essa matéria é Raciocínio Lógico. Às vezes, fica difícil acompanhar o raciocínio desenvolvido em uma explicação textual.
Fica aqui esse apelo!
Resolução da questão pelo professor Helder Monteiro:
https://youtu.be/gMHIFnZy0z0?t=50s
-
X = APENAS empresas que encerram este ano
Y = empresas que encerram este ano e foram abertas em anos anteriores
Z = APENAS empresas que foram abertas em anos anteriores
TOTAL = 2.000 - 200 (nenhum dos casos) = 1.800
X + Y + Z = 1800 -> fórmula do Diagrama de Venn
Y = 1/9X ( pois 1/9 das que encerraram as atividades este ano foram abertas em anos anteriores)
Y = 1/10Z (1/10 das que foram abertas em anos anteriores encerraram as atividades este ano)
Substituindo as fórmulas na principal como um sistema, temos:
X + 1/9X + 10Y = 1800 -> X + 1/9X + 10/9X = 1800 - > 9X + X + 10X = 16200 -> X = 810
Agora ficou fácil, encontraremos os outras variáveis.
Y = 1/9 x 810 = 90
Z = 10Y -> Z = 10 x 90 = 900
Espero que tenha ajudado!
-
Resolvi como a Iris e o Leonardo. A explicação do professor está confusa.
-
Esse tipo de questão toma muito tempo do aluno!
-
A explicação do Leonardo Ribeiro é show! Simples e direta!
-
Eu resolvi do jeito mais simples, sem precisar fazer conta:
Se em um dos termos o divisor é 10 e no outro é 9, quer dizer que um número divido por 10 será menor que um dividido por 9.
Pronto.
-
Parabens Leonardo Ribeiro vc teve o olho de Tandera nessa questao e precisamos disso mesmo, buscar os caminhos mais obgetivos e sólidos q a matematica possa nos oferecer.. A prova é um momento tenso pra qualquer pessoa.
Vamo p cima!!!
-
Resoluçao pelo prof. Helder Monteiro https://www.youtube.com/watch?v=gMHIFnZy0z0&feature=youtu.be&t=50s
-
Questão simples.
Total: 2000, mas 200 não foram abertas nem encerradas (então 2000-200= 1800). Assim:
1) Empresas abertas em anos anteriores: 1/9 de 1800 = 200
2) Empresas que encerraram as atividades: 1/10 de 1800 = 180.
200 é maior que 180, então gabarito certo.
-
Esse professor Vinicius é uma piada. Olha essa explicação dele! Avisem que ele está ensinando fazer questão de concurso público e não para uma tese em graduação de Matemática. Precisamos de dicas, pulos do gato, raciocínios rápidos e resoluções diretas!
-
GABARITO ERRADO
Flávia Jaine, respondeu de forma simples e compreensível.
Alguém avisa para esse professor Vinícius que ele não está desenvolvendo uma tese a
cada questão que ele responde pfv. Os comentários do cara dá umas 2 folhas e mesmo
assim não consigo entender nada do que ele escreve.
QCONCURSOS, COLOQEU OUTRO PROFESSOR PARA RESPONDER AS QUESTÕES
OU PEÇA PARA O VINÍCIUS SIMPLIFICAR AS COISAS E APRENDER DÁ AULA. PQ TÁ DIFÍCIL.
Albert Einstein disse uma vez que " Se vc não consegue explicar
algo de forma simples, é pq vc não entendeu bem a coisa".
_____________________________
-
Cai na tentação de tentar achar a intersecção. =(
Não tem motivo, pois, não há possibilidade de uma empresa ser aberta em anos anteriores e ano atual. Era só deduzir o valor das empresas que não se enquadravam em ambas e calcular.
-
Saudades do Professor Renato!
-
ão entendi nem o enunciado. Pqp.
-
T= 2.000 E= encerradas A= antigas N= 200 (novas e abertas, então não encerradas e não antigas)
1/9 E são A // 1/10 A são E (as duas estão informando a interseção) ->
A interseção com E = E interseção com A -> 1/9E=1/10A -> E/9=A/10 -> 10E/9 = A => A= 10E/9
T = (Só E) + (E interseção com A) + (Só A ) + N
2.000= (E - E/9) + E/9 + (A - E/9) + 200 => 2.000 = E + A - E/9 -200 => 2.000 - 200 = E + 10E/9 - E/9 => 1.800 = E + 9E/9 => 1.800 = 2E => E= 900
Total de encerradas = 900 / Encerradas antigas = E/9 = 900/9 = 100 / Encerradas novas = 900 - 100 = 800
A= 10E/9 => A = 10 * 900/9 => A=1.000 -> Total antigas = 1.000 / Antigas encerradas = 100 / Antigas abertas = 1.000-100 = 900
O número de empresas que foram abertas anos anteriores é maior que o número de empresas que encerraram atividade este ano?
Total de abertas A= 1.000 é maior que Encerradas novas = 800 -> 1000 > 800 (CERTO)
-
CERTO
Se tem uma coisa que aprendi resolvendo esse tipo de questão é começar de trás pra frente, pois a cespe confunde a cabeça das pessoas logo no começo do enunciado, isso é pra bambear o cabra.
200 Empresas não abriram e nem fecharam. Logo, de 2.000 subtrai 200 = 1.800
Enc. esse ano, abriu ano passado -> 1/9 de 1.800 = 1 * 1.800 = 1.800/9 = 200
Enc. ano passado, abriu esse ano. -> 1/10 de 1.800 = 1 * 1.800 = 1.800/10 = 180
Veja enunciado: O número de empresas que foram abertas em anos anteriores é superior ao número de empresas que encerraram as atividades este ano.
Bons estudos!!
-
CUIDADO PESSOAL!!!!!
Os comentarios do Leonardo Ribeiro e da Flávia Jaine estão equivocados!!!
Se não tiverem acesso ao comentário do professor vejam o comentario do Danilo Capistrano!!!!
-
Qconcursos, se for pra comentar questões de raciocínio lógico digitado, nem precisa blz? Isso os colegas concurseiros já fazem muito melhor! vlws.
-
Como o colega adriano comentou, os comentários mais curtidos estão completamente equivocados.
A resolução do professor pode estar um pouco complicada mas está correta.
Não adianta simplesmente chegar no gabarito em rac. lógico, tem que entender a questão pois se cair novamente não podemos depender da sorte.
-
Resolvi pelo mesmo raciocínio do Leonardo Ribeiro e da Flávia Jaine
-
Como 200 empresas não encerraram as atividades este ano e não foram abertas em anos anteriores, podemos dizer que 2000 – 200 = 1800 empresas encerraram as atividades este ano OU foram abertas em anos anteriores. Sejam:
A = conjunto das empresas que encerraram as atividades este ano
B = conjunto das empresas que foram abertas em anos anteriores
n(A ou B) = n(A) + n(B) – n(A e B)
1800 = n(A) + n(B) – n(A e B)
Veja ainda que:
1/9 das que encerraram as atividades este ano foram abertas em anos anteriores, ou seja, 1/9 x n(A) = n(A e B). E 1/10 das que foram abertas em anos anteriores encerraram as atividades este ano, ou seja, 1/10 x n(B) = n(A e B). Isto é,
1/9 x n(A) = n(A e B)
n(A) = 9 x n(A e B)
1/10 x n(B) = n(A e B)
n(B) = 10 x n(A e B)
Portanto,
1800 = 9 x n(A e B) + 10 x n(A e B) – n(A e B)
1800 = 18 x n(A e B)
n(A e B) = 1800 / 18
n(A e B) = 100
Logo,
n(A) = 9 x n(A e B) = 9 x 100 = 900
n(B) = 10 x n(A e B) = 10 x 100 = 1000
Portanto, 900 empresas foram encerradas este ano, e 1000 foram abertas em anos anteriores, tornando o item CORRETO.
-
Caramba! 20 minutos nessa questão, a cabeça doeu...
-
Perfeito comentário de Ricardo Borges - Goiás!
-
Certo.
A maior dificuldade talvez seria entender o que a questão pede, depois fica simples.
Regra básica:
quem DIVIDE MAIS fica com MENOS -> 1/10 = 0,1
quem DIVIDE MENOS fica com MAIS -> 1/9 = 0,111
Pronto já sabemos que as empresas que foram abertas em anos anteriores correspondem a 1/9 sendo MAIOR que 1/10 das empresas que encerraram as atividades esse ano.
-
Galera, vocês estão confundindo os dados, aqui vai a resolução da questão:
Em um grupo de 2.000 empresas, 1/9 das que encerraram as atividades este ano foram abertas em anos anteriores, 1/10 das que foram abertas em anos anteriores encerraram as atividades este ano e 200 empresas não encerraram as atividades este ano e não foram abertas em anos anteriores.
O número de empresas que foram abertas em anos anteriores é superior ao número de empresas que encerraram as atividades este ano.
Primeiramente, a questão não quer saber o número de empresas que encerraram noano e são de anos anteriores, mas sim o total das empresas. Percebam:
Total de empresas analisado: 2000
Empresas que não encerraram: 200
Empresas que encerraram as atividades este ano: 1800, destas 1/9 encerrou as atividades, ou seja, 200.
Essas 200 equivalem a 1/10 das empresas que foram abertas em anos anteriores, portanto, há 2000 empresas que foram abertas em anos anteriores.
Voltemos à assertiva:
O número de empresas que foram abertas em anos anteriores é superior ao número de empresas que encerraram as atividades este ano.
Gab.: CERTO.
2000 > 1800
-
Galera!! A questão não é díficil, só precisa ser muito organizado.
Montem uma tabelinha com as informações que facilita muito na resolução.
/ Novas / Velhas
Vivas / 200 / 9/10 do total de velhas
Mortas / 8/9 M / 1/9 M e 1/10 do total de velhas
Agora só igualar o número de mortas com o número de velhas.
1/9 M = 1/10 V
Pensando que a soma das 4 células da tabela obrigatoriamente tem que chegar no valor de 2000:
2000 = 200 + 9/10 V + 1/10 V + 8 x (1/10 V)
1800 = 18/10 V
V = 1000
Opa! encontramos o número de empresas velhas, maravilha! Agora só completar o que falta:
/ Novas / Velhas
Vivas / 200 / 9/10 do total de velhas = 900
Mortas / 800 / 1/9 M e 1/10 do total de velhas = 100
Quantas encerraram esse ano? R. 800 + 100 = 900
Quantas foram abertas em anos anteriores? R. 100 + 900 = 1000
Sendo 1000>900 a resposta é CORRETA.
-
CERTO
Sem muito mimimi.
TOTAL DE EMPRESAS = 2000 - 200 (QUE PULARAM FORA DA QUESTÃO)
1800 - 1/9 = 200 (EMPRESAS ABERTAS ANOS ANTERIORES)
1600 - 1/10 = 160 (EMPRESAS QUE ENCERRARAM ATIVIDADE ESSA ANO)
-
Errei a questão por não saber a diferença entre: empresas que abriram em 2020 e fecharam em 2021 e empresas que fecharam em 2021 e abriram em 2020.
-
2000 empresas.
“1/9 das empresas que encerraram esse ano foram abertas em anos anteriores.”
“1/10 das empresas que foram abertas em anos anteriores, encerram as atividades esse ano.”
“200 → Não encerraram as atividades esse ano e não foram abertas em anos anteriores.”
Pergunta:
Foram abertas > Encerraram?
Vamos nomear as empresas:
A = Encerraram...
B = Foram abertas...
Vamos relembrar a fórmula abaixo:
N(AUB) = N(A) + N(B) – N(AႶB).
Pensando: Se eu tenho 2 mil empresas, e 200 delas são (~A Ⴖ ~B), quanto sobra das empresas que são (AUB)? Serão 2mil – 200 = 1800.
1800 = A + B – (AႶB)
Vamos agora identificar aquelas frações e muita atenção agora porque é nisso que o examinador quis te pegar.
O que representa (AႶB)?
As empresas que encerraram... e que foram abertas...
Logo, se eu digo: “1/9 das que encerraram...foram abertas....”.
Eu quero dizer: 1/9A = (AႶB), já que 1/9 dessas empresas também foram abertas, ou seja, eles fazem parte desse grupo seleto interseccionado. Então:
1/9A= (AႶB) → A = 9 (AႶB)
Por conseguinte, a afirmação abaixo também pode ser escrita:
1/10B = (AႶB) → B = 10 (AႶB)
1800 = 9(AႶB) + 10(AႶB) - (AႶB).
(AႶB) = 100
A = 900
B = 1000
Voltemos a pergunta:
Foram abertas... > Encerraram...? B > A?
A = encerraram.
B = foram abertas.
A= 900
B = 1000
1000 > 900? Sim (correto).
-
Boa noite gente,
Esta questão não é tão simples quanto parece...não se resolve apenas calculando as frações como muitos demonstraram. Cuidado com os comentários equivocados, não é só chegar na "resposta", porque chegar no gabarito por um caminho errado pode te fazer utilizar o raciocínio errado em uma questão da prova...aí já era! =/
A resolução do Jonatas Zanco está correta.
Abraços e bons estudos!