-
Item certo.
Preciso de 1 coordenador / 1 relator / 1 técnico.. dentro de 15 servidores, então:
15 x 14 x 13 = 2730 maneiras
-
Permita-me discordar;
Na questão é necessário tirar os elementos repetidos, ou seja, 15*14*13/3*2*1. Do contrário, estariamos pensando que um grupo formado por: um coordenador,um relator e um técnico seria diferente de um grupo formado por: um relator, um coordenador e um técnico,
-
Concordo com o Jorge. Resolvendo a combinação o resultado seria 455.
(C 15,3 = 15!/ 3! . 27!)
-
http://www.youtube.com/watch?v=tfz4Zd_mzXo
a parti de19'06"
-
Galera, isso é questão de ARRANJO, a ordem IMPORTA, portanto a resolução está correta!
A15,3 = 15!/12!
ou
15 x 14 x 13
=2730!!!
Questão corretíssima!!!!
Gabarito definitivo cespe: C
-
Me ajuda, eu não entendi. O meu cálculo de 455.
Arranjo? Ele tira 3 servidores do grupo de 15... O certo seria combinação.
-
resposta 2730
quantas equipes posso montar sendo que deva prevalecer (um coordenador, um relator, um técnico)
Se temos 15 servidores
1) então tenho 15 possibilidade para ser coordenador
2) se ja escolhemos o coordenador então restou 14 possibilidade para escolher o relator
3) escolhendo o coordenador e o relator sobrou 13 possibilidade
logo,
15 X 14 X 13 = 2730
-
Vamos reunir os elementos necessários para a resolução da questão! Temos 15 servidores e temos que formar 03 equipes compostas por 01 coordenador em uma, na outra 01 relator e na última 01 técnico. Questão de combinação... Vamos lá:
01 coordenador (C 15,1 = 15);
01 relator (C 14,1 = 14);
01 técnico (C 13,1 = 13).
Como existe uma sucessão de escolhas usamos o príncipio multiplicativo, multiplicando assim os resultados de todas as etapas (15.14.13 = 2730).
Obs: Cada casa que andamos perdemos 01 servidor, vejamos que no primeiro caso escolhemos 01 coordenador, no segundo caso ficamos somente com 14 dos 15 totais, por que já tinhamos escolhido um, então ficamos somente com 14 possibilidades para escolher 01 relator e no terceiro caso ficamos somente com 13 possibilidades por já termos escolhidos 02 servidores nos casos anteriores... Bom, tentei explicar da melhor maneira, galera :)!
Boa sorte a Todos!
-
Multiplica-se a combinação de 15, 3 pela permutação de 3 (3!)
Isso pq existem 3! maneiras de se dividirem os cargos em cada grupo de 3.
ou seja:
455 * 6 = 2.730
-
Concordo com quem analisou como ARRANJO!
-
Gente, a ordem importa! É 1 coordenador,1 relator e 1 técnico. Portanto NÃO é combinação,é arranjo simples!
15x14x13= 2730 Questão Correta!!
-
Há ordem, logo trata-se de Arranjo. Caso fosse todos os cargos iguais (técnico por exemplo), seria combinação, hipótese em que deveria-se dividir pelo fatorial do número de elementos a ser escolhido, 3 na questão em pauta!
-
É claro que a ordem importa! "Vou" pegar vc e "rebaixar" de COORDENADOR para técnico, dai vc me diz se a ordem importa ou não importa....
-
Não precisa nem colocar em fórmula do Arranjo.
É só fazer a multiplicação: 15 x 14 x 13 = 2730 maneiras
-
Olha só, primeiramente eu também fiz combinação e o resultado deu 455.
Vi que esse resultado era muito longe do que a questão deu "2.500".
Quando acontecer isso, 99% de vc ter resolvido errado.
Questões do cespe sempre dão o resultado perto do que a questão afirma.
Daí fui resolver por arranjo e pronto, resultado: 2730. É isso, certa resposta.
Não é preciso somente saber a teoria, tem que saber resolver questões.
-
Wellington Fabiano
Boa boa, nem fui pela ordem tinha até esquecido.
Mas resolvi da seguinte forma 15x14x13 = 2730, maneiras distintas.
Se não importasse a "distinção" seria 15x15x15
GAB CERTO
-
Dica: falar em profissão=ARRANJO
-
Mais simples ainda, é possível resolver a questão pelo Princípio Fundamental da Contagem.
A ordem importa? Talvez
Ele quer o coordenador primeiro, ou o relator ou o técnico = 15 possibilidades;
Escolhido 1 coordenador, ou 1 relator, ou 1 técnico sobram = 14 possibilidades;
Escolhidos 1 técnico e 1 coordenador, ou 1 coordenador e 1 relator, ou ainda 1 relator e 1 técnico, sobram = 13 possibilidades.
Então : 15 . 14 . 13 = 2730.
Gabarito = Correto
-
O enunciado deixa claro que cada equipe deverá
ser composta por um coordenador, um relator e um técnico, nesta ordem. Logo,
quando a ordem importa, utilizamos Arranjo Simples, assim:
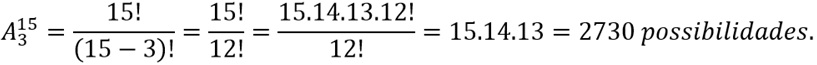
RESPOSTA: CERTO
-
15 servidores
1 coordenador = 15
1 relator = 14
1 técnico = 13
15x14x13 = 2730
Resposta correta!!
-
Respondi nesse mesmo raciocínio Queren Duarte.
-
Basta perceber que a questão é resolvida através de arranjo simples e não de combinação, já que os mesmos 3 servidores podem formar equipes distintas, ocupando posições diferentes.
Então, o cálculo fica assim:
A15,3 = 15 x 14 x 13 = 2730. Gabarito CERTO
OBS.: Se a questão não explicitasse que cada equipe possui 3 cargos distintos, seria uma combinação. Nesse caso o cálculo seria assim: C15,3 = 15 x 14 x 13 / 3 x 2 x 1 = 455. O que tornaria o gabarito errado.
-
Temos 15 servidores para formar equipes de 3 com funções especificadas, logo a mudança de posição gera um resultado diferente veja:
Coordenador ---> Pedro
Relator ----> José
Técnico ----> Antonio
é diferente de:
Coordenador ---> José
Relator ----> Antonio
Técnico ----> Pedro
- Então temos um arranjo simples que se resolve: 15 x 14 x 13 = 2.730.
-
Cada vez que eu seleciono um cargo para uma pessoa a próxima opção será diminuída uma unidade, pois a mesma pessoa não pode ocupar dois cargos (daí a especificação do começo).
-
Observem também que os valores propostos nas questões CESPE geralmente se aproximam dos valores encontrados nos resultados dos cálculos, logo uma diferença muito grande entre eles pode ser indício de erro.
--- Vamos deixar suor pelo caminho.
-
Pessoal, tenho visto aqui certa incompreensão na interpretação da questão. Nesse caso a ordem de escolha dos servidores não importa , ou seja C+R+T=R+T+C=T+C+R... O que não pode é ter mais de um cargo igual. E por isso a questão é de arranjo , pois embora a ordem de DISPOSIÇÂO dos escolhidos não importa, a ordem de ESCOLHA importa. Portanto:
A15,3= 15!/15-3!=2730
-
Naylane, fiz da mesma forma que vc. Tive um professor que falava assim : Meu filho, não sabe as formulas neh, tente pelo principio da contagem e pense um pouquinho....sempreee dá certo.
-
Arranjo não cai no INSS. Tô de boas.
-
Gente, esse tipo de questão cai na prova do INSS?
-
An,p = n! A15,3 = 15! A15 = 15! A15 = 2.730
- ------ ------ -------
(n-p)! (15-3) 12!
-
para mim não está claro que os cargos são fixos...
-
Gabarito: CERTO
Trata-se de um Arranjo - A(15,3)
A(15,3) = 15!
____________
(15-3)!
= 15x14x13x12!
______________
12!
=2.730.
Obs: Formação de equipe com função a ordem importa, por isso utiliza-se a fórmula do arrajo.
-
Dá para fazer por combinação, o detalhe é que tem de multiplicar por uma permutação depois. Resolvi da seguinte forma:
C(15,3) = 15 x 14 x 13 / 3 x 2 x 1 = 455 (pois há 15 servidores, mas queremos escolher apenas 3)
Como cada servidor pode ser um coordenador, um técnico ou um relator (e nesse caso, a ordem importa), fazemos uma permutação de 3.
3 x 2 x 1 = 6
Depois multiplicamos os dois resultados: 455 x 6 = 2.730
Obs: Dá para fazer por arranjo também, comentei só para mostrar como daria para fazer por combinação ;)
Abraços! Bons estudos
-
Segui os ensinamentos do mestre Josimar Padilha e deu certo, adotando o método do princípio da contagem:
A quantidade de maneiras distintas de serem escolhidos 3 dos referidos servidores
São 15 servidores, logo a conta ficaria da seguinte forma: 15 x 14 x 13 (já que a ordem importa)
RESULTADO: 2730...gabarito CERTO
-
CORRETA
A15,03
15! / 15! - 03! = 12!
15*14*13=2730
-
Melhor explicação (e ainda com dicas). Prof. Helder Monteiro
https://www.youtube.com/watch?v=tfz4Zd_mzXo
A partir de 19min
-
Arranjo: ele tenha confundir querendo fazer pensar que são 3 cargos iguais, mas a equipes tem que ser formadas por três cargos diferente ditos acima.
15*14*13= 2730
-
Podemos escolher os 3 servidores que formarão uma equipe através
da combinação dos 15 servidores em grupos de 3, ou seja,
C(15,3) = 15 x 14 x 13 / 3!
C(15,3) = 15 x 14 x 13 / 6
C(15,3) = 5 x 7 x 13
C(15,3) = 455
Assim, é possível montar 455 trios diferentes de servidores. Em
cada um desses trios, devemos permutar os 3 servidores entre si, entre
os cargos de coordenador, relator e técnico. Assim, temos P(3) = 3! = 6
organizações diferentes entre os tres servidores de cada trio, totalizando
455 x 6 = 2730 formas de montar as equipes.
-
Concordo com o raciocínio do colega Resende.
Trata-se de uma combinação.
A assertiva questiona a quantidade de maneiras distintas de se escolher 3 diferentes servidores para formar 1 GRUPO, LOGO NÃO IMPORTA A ORDEM DESTE GRUPO ZÉ, A MARIA E O CHICO, OU CHICO, ZÉ E MARIA, DESDE QUE O TOTAL SEJA 3 PESSOAS.
Esse é meu sensato ponto de vista.
-
Olá pessoal,
Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/2y-7MhxHeyk
Professor Ivan Chagas
Gostou? https://pag.ae/blxHLHy
-
Não se trata de combinação, pois a ordem importa. Perceba que, se tivermos, por exemplo, servidores A, B e C, o servidor A sendo coordenador em um grupo é diferente de um outro grupo com o servidor A sendo relator ou técnico.
Trata-se de arranjo. P = 15 x 14 x 13 = 2730
-
Questão mal formulada, pois não informou que a função será dada através da ordem de escolha. lamentável.
-
GABARITO CORRETO
Pessoal, se trata de ARRANJO, pois a ordem importa. A questão especificou as funções de cada membro da equipe : um coordenador, um relator e um técnico.
Seria combinação, se a questão tivesse pedido apenas de quantas formas distintas podemos compor uma equipe de 3, dentro do total de 15 servidores.
Espero poder ter ajudado.
Bons estudos a todos!
-
Discordo com o Gab;
A questão não deixou claro que os cargos são fixos, logo qualquer um poder ser coordenador, relator e técnico;
Para mim, trata-se de Combinação.
Gab Errado.
-
Funções diferentes é "arranjo" 15 para escolher 3=15x14x13=2730
Se fosse funções iguais usariamos "combinação".
-
Podemos escolher os 3 servidores que formarão uma equipe através da combinação dos 15
servidores em grupos de 3, ou seja,
C(15,3) = 455
Assim, é possível montar 455 trios diferentes de servidores. Em cada um desses trios, devemos
permutar os 3 servidores entre si, entre os cargos de coordenador, relator e técnico. Assim, temos
P(3) = 3! = 6 organizações diferentes entre os três servidores de cada trio, totalizando 455 x 6 = 2730
formas de montar as equipes.
fonte.: estratégia concursos
-
Para mim, trata-se de combinação. Em momento algum da situação hipotética foi falado que haveria ordem.
-
na verdade é combinação, mas nesse caso cada integrande pode ser coordenador, relator ou
-
Na verdade trata-se de uma combinação. Cada um pode ser coordenador, revisor ou técnico, já que a questão nao informou a quantidade
de pessoas que são coordenadores, revisores ou técnicos. Logo:
C(15,1) * C(14,1) * C(13,1) = 2730 maneiras
-
Item Correto.
Em nenhum momento a questão fala sobre uma ordem na questão. A pessoa escolhida pode ser designada para qualquer uma das três funções, assim, sabe-se que é possível permutar as três. Logo:
C15,3 x 3! = 2730.
-
Gab C
Maneiras distintas, basta saber que a ordem não importa logo só vai diminuindo, lembre-se são três apenas a serem escolhidos.
15 x 14 x 13 = 2730
-
Fiz com combinação e deu boa kkk
C15,1; C14,1; C13,1 = 2730 formas de montar a equipe
-
Como o enunciado define que cada equipe deve ser composta por um coordenador, um relator e um técnico, e que há 15 servidores; somos induzidos ao erro de concluir que haverá 5 equipes e cada uma com um de cada...
Entretanto, não se afirma isso, logo:
C15,1 * C14,1 * C13,1 = 2730 maneiras
PORÉM, caso a questão tivesse definido que dos 15 servidores, há exatamente 5 coordenadores, 5 relatores e 5 técnicos, a resolução seria essa:
C5,1 * C5,1 * C5,1 =125 maneiras
De qualquer forma o enunciado entra em contradição com a questão, e pra mim haveria sim possibilidade de anulação.
-
dica: vejam o comentário da Naylane .
-
São funções diferentes, logo, é questão de ARRANJO = A15,3 ou 15x14x13=2730.
Qualquer erro, mande uma mensagem.
Não desista!!!
#AVANTE
#VAMOSCONSEGUIR
-
Gabarito Certo
⨠ Lembrando que são funções diferentes (Arranjo), posto que são 3 cargos específicos (coordenador, relator e técnico), logo:
A15,3 = 15.14.13 = 2130.
As resoluções feitas por combinações foram mera coincidência, mas a fórmula correta é a de Arranjo. Bons estudos!!
-
Acredito que os que erraram, (inclusive eu) havia feito combinação, não me atentei que os 3 são para cargos diferentes
-
EU FUI PRA FAZER COMBINAÇÃO, DAÍ FIZ 15X14X13 e deu 2.730, parei e pensei, deve ser ARRANJO, pq o resultado sempre está próximo
-
Gabarito CORRETO
15*14*13 = 2730.
2730 > 2500.
-
"cada equipe deverá ser composta por um coordenador, um relator e um técnico".
São cargos com atribuições DISTINTAS. Logo, a ordem dos elementos importa.
-total de funcionários=15
-eu seleciono 3 desses 15, e cada um com uma função diferente.
A (15,3)=2730
-
Se a ordem importa, só multiplica.
-
O núcleo da questão era saber que a ORDEM IMPORTA! Ou seja, é ARRANJO
-
As questões desse mesmo "problema" de planejamento de ações de auditoria são boas para treinar Combinação e Arranjo.
obs: Q392184
-
Eu resolvi conforme o comentário que o professor fez em uma outra questão semelhante, mas nessa ele seguiu outra linha.
A questão fala que são 15 servidores e quer uma equipe com 3, então a ordem não importa e faz uma combinação:
C15,3= 455
Porém, a questão fala que nessa equipe há: 1 coordenador, 1 relator e 1 técnico, nesse caso, a ordem irá importar. Então eu fiz um Arranjo, por meio do PFC (Princípio Fundamental da Contagem):
3 x 2 x 1 = 6
Multiplicando 455 x 6 = 2.730 possibilidades.
-
Resolução para quem começou a pouco tempo:
- Total de servidores: 15
- Função 1: Coordenador
- Função 2: Relator
- Função 3: Técnico
Por que a ordem importa?
- Isso acontece porque os servidores escolhidos vão ocupar funções distintas, como discriminado acima, logo, a ordem vai importar.
Obs: Se a questão falasse que deveríamos selecionar apenas 3 pessoas para participar do GRUPO, todos iriam ter a mesma função, participar do GRUPO, por isso a ordem não importaria, mas perceba que não é o que a questão quer, ela deixa explícito que cada um vai ocupar um cargo diferente.
Portanto, se não podemos repetir, a ordem importa e não vamos usar todos os servidores disponíveis, trata-se de um arranjo.
Obs: Seria permutação se eu fosse usar os 15 servidores.
Arranjo: 15 x 14 x 13= 2730
Qualquer erro, só sinalizar que retifico.
-
C(15,3) = 15.14.13 / 3.2.1 = 455
455 equipes podem ser formadas. Agora é necessário colocar uma função para cada um :
permutação de 3, pois 3 tem chances de ser coordenador, 2 de relator e 1 de técnico (3!) = 6
455 . 6 = 2730