-
Pessoal, eu fiz dessa forma e não sei o raciocínio presente está correto. Vamos à resolução:
78 apertos de mãos
2 mãos + 1 uma única vez, logo: 78 / 3 = 26 / 2. Lembrando que o 2 representa a quantidade de mãos = 13
Se eu estiver errada, por gentileza, me corrijam .
-
Resolvi por eliminação de alternativas...
13 pessoas = 12 apertos que uma pessoa realiza
12+11+10+9+8+7+6+5+4+3+2+1 = 78
Não podemos esquecer que "A cumprimenta B" é igual a "B cumprimenta A"
O exercício pode ser feito somando os números... 1+2+3+4+5+6+7... até chegarmos ao valor de 78 apertos de mão.
-
Eu fiz usando a fórmula Cn,p=78, como p=2 é só substituir na fórmula.
78= n!/(n-p)!p! ----> 78= n.(n-1).(n-2)!/(n-2)!.2! ---->156=n²-n, joga na fórmula de baskhara e chega ao resultado de 13.
-
Alguém propõe alguma outra maneira de resolver esta questão?
Resolvi como o nosso colega Dreyfus fez, mas marquei a resposta como 12 e não como 13. Não entendi o pq ser 13.
-
78/13=6 logo o mesmo cumprimentou 6 pessoas distintas, pois se tentar dividir pelas outras alternativas não dará exata, ok.
-
Sendo n o número de pessoas e cada uma cumprimenta a outra 1 vez, temos então a equação (n*(n-1))/2 = 78
Obs.: n-1 porque uma pessoa não cumprimenta ela mesma e dividimos por 2 para não contar duas vezes o mesmo cumprimento - p1 cumprimenta p2 = p2 cumprimenta p1.
Desenvolvendo chegamos a equação do 2º grau (n^2 = n elevado a 2):
n^2 -n -156 = 0
Aplicando a fórmula de báskara [ n = (-b +-sqrt(b^2-4ac)) / 2a] (sqrt = raiz quadrada)
n = (1 + sqrt (1+4*156))/2 [desprezando o resultado negativo]
n = (1+25)/2n = 13 pessoas
-
Na dúvida da resolução desenhe, o X representa os 78 apertos de mãos realizados.
Sem repetições por 13 pessoas.
| . | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | . | x | x | x | x | x | x | x | x | x | x | x | X |
| 2 | . | . | x | x | x | x | x | x | x | x | X | X | X |
| 3 | . | . | . | X | x | x | x | x | x | x | X | X | X |
| 4 | . | . | . | . | x | x | X | x | X | x | X | X | X |
| 5 | . | . | . | . | . | X | X | X | X | x | X | X | X |
| 6 | . | . | . | . | . | . | x | X | X | X | X | X | X |
| 7 | . | . | . | . | . | . | . | X | X | X | X | X | X |
| 8 | . | . | . | . | . | . | . | . | X | X | X | X | X |
| 9 | . | . | . | . | . | . | . | . | . | X | X | X | X |
| 10 | . | . | . | . | . | . | . | . | . | . | X | X | X |
| 11 | . | . | . | . | . | . | . | . | . | . | . | X | X |
| 12 | . | . | . | . | . | . | . | . | . | . | . | . | x |
| 13 | . | . | . | . | . | . | . | . | . | . | . | . | . |
-
Com a forma inicial do "Luciano", resolvi pelas alternativas. Para ganhar tempo iniciei pela alternativa 14 que está no meio...como deu a mais, fiz pelo 13, e deu certo:
n * (n - 1) / 2 =
13 * (13 - 1) / 2 =
(13 * 12) / 2 =
156 / 2 = 78 apertos de mãos.
Jesus é Senhor.
-
+ simples...78:2= 39:3=13:1=13.
-
Para começar a entender a questão, parti da seguinte situação: Se fossem 3 participantes, cada um só poderia cumprimentar duas pessoas, logo o número de participantes (n) deverá ser multiplicado por (n-1), para descobrirmos a quantidade de cumprimentos.
Então, indo direto para a resposta (13), ficaria 13x12=156. Esse valor deve ser dividido por 2, pois, por exemplo, quando A cumprimenta B, B também cumprimenta A. Logo 156/2= 78.
Espero que tenham entendido.
-
Questão de Análise Combinatória
Total = 78 apertos de mão
x pessoas / 2 pessoas por aperto de mão
Fórmula para combinação:
C n,p = n!
p! (n-p)!
C x,2 = x! . (x-1) . (x-2) = 78
2! (x-2)!
x (ao quadrado) - x = 78
2
156 = x (ao quadrado) - x
Chegando aqui você tem duas opções: ou transforma numa equação do
2º grau e resolve (x (ao quadrado) - x - 156 = 0) ou substitui o x pelas
alternativas da questão:
156 = 13 (ao quadrado) – 13 = 156
Resposta: B
-
Na primeira explicação porquê é acrecentado (x-1).(X-2) na fórmula?
-
Marcelo Cunha, estava fazendo o mesmo calculo q fez, mas parei dividindo 39 por 2....pq dividiu por um depois?
-
Sem fórmula é mais fácil:
Imaginei uma pessoa cumprimentando outras 11 pessoas (comecei pela letra A = 12). a 1ª pessoa cumprimenta 11 pessoas; a 2ª pessoa cumprimenta 10 pessoas (pq ela já cumprimentou a 1ª); a 3ª pessoa cumprimenta 9 pessoas (pq ela já cumprimentou a 1ª e a 2ª pessoa) e assim por diante. construindo a soma:
11+10+9+8+7+6+5+4+3+2+1 = 66 apertos de mão. Não é a resposta.
Segui o mesmo raciocínio para a letra B 13 pessoas:
12+11+10+9+8+7+6+5+4+3+2+1= 78 apertos de mão. Resposta correta!
-
13 x 12/ 2 = 78 apertos de mão
-
Utilizando
a fórmula da análise combinatória:
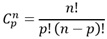
Onde
n = número de pessoas e p = o número de aperto de mão por pessoa, assim:
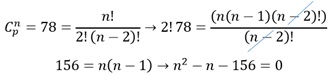
Sabemos que n é o
número de pessoas que queremos, logo basta substituir as opções dadas na
questão na equação acima ou a resolver por Bhaskara.
Quando substituimos o
valor da letra b na equação a mesma zera, logo nossa resposta é a letra b, ou
seja, 13 pessoas.
13²
- 3 - 156 = 0
Resposta: B.
-
1º) Questões de aperto de mãos são questões de combinação, pois a ordem não importa.
Ex: João cumprimenta Pedro = Pedro cumprimenta João.
2º) Um aperto de mão é feito por duas pessoas. Destarte, temos o nosso "p", que no caso é 2.
C n,p ---> C n,2
3º) Agora para descobrir o "n" - que no caso é o número de participantes - é só ir pelas alternativas dadas pela questão:
Alternativa "A": 12 participantes ---> n = 12.
C 12,2 = 66 ---> Resposta errada.
Alternativa "B": 13 participantes ---> n = 13.
C 13,2 = 78 ---> Resposta certa.
(13 x 12) / 2 = 78.
Gabarito letra: B.
-
Minha maneira foi ir pelas alternativas: C12,2 = 66 , C 13,2 =78 .... assim sucessivamente.
-
C x,2 = 78
x! / 2 = 78
x! = 78x2
x! = 156
Daí utiliza o método da tentativa em cada uma das alternativas:
obtendo-se: 13 x 12 = 156
Letra: B)
-
Simples, basta decompor 78 no MMC
-
Fiz sem formula, somando 1 + 2 + 3 +4 +5 +6 +7 +8 +9 +10 +11 +12 =78, pra 12 apertos 13 pessoas...
Abraços
-
é preciso duas pessoas se cumprimentarem para 1 aperto de mão, entao: 78/2 = 46 participantes que cumprimentaram os demais uma unica vez, entao: 46/2 = 13 :)
-
Louise quando que 78/2 é 46??? talvez, seja no mesmo dia em que 46/2 for 13, né!? #Contasobrenatural!
-
Fiz da seguinte maneira 13 + 12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 78
A única alternativa que chegaria a essa soma total(78)
Letra B
-
Basta decompor o número e encontrar seu máximo divisor, no caso temos 2x3x13. Daí temos que ter no mínimo duas pessoas e no máximo 13.
-
Resolvi a questão indo pelas alternativas e vendo quando cada uma delas impunha de apertos de mãos, também; mas de outro modo também interessante: descobrindo quanto cada participante, individualmente e após o anterior, apertaria as mãos dos demais. Isso se transforma uma P.A., então utilizei a fórmula da soma dos termos da P.A. Interessante perceber que o resultado é o mesmo que resolver por combinação, dá certinho!
Magias da matemática.
-
C13,2 = 13!x12! / 2!
C13/2 = 13x6
C13,2 = 78
-
x pessoas
I - Cada pessoa aperta a mão de outra pessoa então "x" possibilidades vezes (x-1) possibilidades.
(x/2)*((x-1)/1)=78 apertos
x(x-1)=78*2
x²-x=156
x²-x-156=0 (caimos nesta equação do 2º grau)
a=1 / b=-1 / c=156
II - Usando báskara
delta =raiz[(-1)²-4*1*(-156)]
delta = raiz[1+624]
delta=raiz=[625]
delta=25
resolvendo báskara
x' = (b+delta)/(2*a)
x' = 1+25/2*1
x'=26/2
x'=13
Resposta "b" mole, mole
x'' será negativo então nem vamos perder tempo.
-
A ordem não importa:
Testando com 13 por 2! (dois fatorais), pois são duas pessoas, para que ocorra o aperto de mão.
13 x 12/ 2.1
13 x 6 = 78 pessoas.
-
Assim é melhor:
São necessárias 2 pessoas para cada aperto de mão, e a ordem não importa: __ . __ = 78
2 1
Como o objeto da questão é a quantidade de pessoas, vou chamar as possibilidades de x:
_x_ . _x-1_ = 78
2 1
x . (x-1) = 78.2 --> x . (x-1) = 156
Depois utilizei as próprias alternativas da questão para saber qual numero vezes seu antecessor (x . x-1) é igual a 156
13 x 12 = 156
Resposta letra B
-
Pessoas explicando com 3 linhas e pessoas explicando com 20 linhas kkkkkkkkkkkkkkkkk
-
Pegando o 78 e dividindo pelas alternativas:
78/12 = 6,5 - ora, não existe "meia pessoa"; então tá errada
78/13 = 6 - Número inteiro. \º/
78/14 = 5,57 - errada
78/15 = 5,2 - errada
78/16 = 4,88 - errada
-
Não há dificuldade nem motivo para explicar esta questão em 20 linhas. Basta utilizar a quantidade de apertos de mão 78 e dividir pelas alternativas do enunciado. Com isso, a alternativa b)13 é a única que o resultado é inteiro satisfazendo assim um aperto de mão por 2 pessoas "inteiras", pois não existe pessoas fracionadas por enquanto.
-
O único número que é divisível por 78 dentre os das alternativas é o 13. 78/13 = 6
-
A alternativa correta é a única divisível por 78. No momento do aperto, quando não se souber por onde começar, pode ser interessante pensar em outas saídas.
-
Caralho teve gente usando até fórmula de Báskara. kkkk. Pow uma simples combinação já rolava.
-
Fiz uma lógica com grupo de 5:
O primeiro comprimenta todos = 4
O segundo o restante = 3
O terceiro = 2
O segundo = 1
Logo no grupo de 5 seriam: 4+3+2+1 = 10 apertos. Daí faça o inverso para 78 apertos: 78-1-2-3-4-5-6-7-8-9-10-11-12 = 0
ou seja, último número foi 12, logo são 13 pessoas.
-
Gabarito Letra "B"
Como o Aperto de mãos é entre duas pessoas, iremos fazer um combinação com 2, assim fizemos teste com as alternativas, e chegamos que a Comibação C (13,2), chegou a resultado de 78 apertos de mãos.
C (n,m) = n! / m!. (n-m)!
C (13,2) = 13! / 2!(13-2)!
C (13,2) = 13! / 2! . 11!
C (13,2) = 13. 12. 11! / 2! . 11!
C (13,2) = 156 / 2
C (13,2) = 78
-
Resolvi a questão sem usar fórmula alguma. Fui usando na tentativa e erro as opções de resposta Usei o seguinte raciocínio:
No grupo de 12 pessoas: O primeiro aperta a mão de todos (menos 1 pois ele não cumprimenta ele mesmo), o segundo aperta a mão de todos - 2 (pois já apertou a mão do primeiro e não cumprimenta ele mesmo), o terceiro aperta a mão de todos - 3 (já apertou a mão do primeiro e a do segundo e não cumprimenta ele mesmo), e assim por diante. Então se fizer 11+10+9+8+7+6+5+4+3+2+1 = 66 -> letra A errada
No grupo de 13 pessoas: 12+11+10+9+8+7+6+5+4+3+2+1 = 78 -> Resposta correta, letra B
-
Combinação do numero de participantes (X), de 2 em 2, que da 78.
C (n,m) = n! / m!. (n-m)!
C (x,2)=78
C (x,2) = x! / 2! . (x-2)!
= x . (x-1) . (x-2)! / 2 . (x-2)!
= x . (x-1) / 2 = 78
x^2 - x - 156 = 0 (equação de segundo grau)...
ou
x . (x-1) = 156
teste todas as alternativas substituindo no x.
x = 12, 12.11 = 132
x= 13, 13.12 = 156
x = 13
Resposta: B
-
Ivan chagas,cadê vc meu filho !
-
nas questões assim meio malucas busca a resposta nas alternativas, a única que da o resultado 78 é a letra B , C13,2 .
-
Eu não sabia o que fazer e simplesmente procurei um divisor de 78 kkk
-
Eu fiz 78/2= 39 e fiz 39/3 kkk deu 13 não sei de onde eu tirei o 3!
-
RESPONDI DA SEGUINTE FORMA: C(13,2) C(13X12) / 2 (156/2) = 78