-
danilo so errou em uma coisa... sao 15 turistas vamos ter que tirar 8 pra C15,8 vai sobrar 7 sendo assim para o barco amarelo fica C7,7
logo
C15,8 * C7,7
-
N= 15
TURISTAS
P1= 8
TURISTAS NO AZUL
P2= 7 TURISTAS NO AMARELO
C15,8=15!/8!(15-8)! => 14.13.12.11.10.9.8!/8! 7! =>
2.13.12.11.10.9 => 308.880
C7,7=7!/7!(7-7)! => 1
-
Senhores,
O João Batista é o único que desenvolveu de forma correta,
porém não concluiu o resultado.
Vejamos:
N= 15 TURISTAS
P1= 8 TURISTAS NO AZUL
Logo,
C15,8
P2= 7 TURISTAS NO AMARELO
Sobraram apenas 7 Turistas
Logo,
C7,7 (É combinação, pois a ordem não importa)
Então ficaria,
C15,8 E (Vezes) C7,7 (vale 1, pois seria 7!/7!)
Então basta desenvolver apenas o C15,8 que obteremos o
resultado
Seria 15X14X13X12X11X10X9X8/(dividido)8X7X6X5X4X3X2X1 = 5995
A questão fala que a resposta seria inferior a 8² X 7² =
3136
Porém o total ficou em 5995 maneiras distintas!
Lembre-se, quando o resultado for muito distante algo está
Errado, pois o CESPE sempre dá um valor bem próximo.
"Se queres algo, faça acontecer"! Hurra!
-
Resultado de Fabrício está com um erro na combinação de C15,8 não é 5995, resultado correto é 6435, superior ao valor dado na questão.
-
Gente não estou entendendo, ele pede para responder com base na situação, e na situação não é possível um barco com menos que 3, estão não existe possibilidade (0%) de se escolher 8 em 1 barco e 7 no outro, pois ai o terceiro não poderia sair.
-
ERRADO
Pessoal não precisa fazer o cálculo das combinações não. Basta abrir as combinações e comparar os valores com o proposto nas questões:
C 15,8 * 7! = 15!/8!7!*7! = 15!/8! = 15*14*13*12*11*10*9*8!/8! = 15*14*13*12*12*11*10*9 > 8*8*7*7
-
Samuel, realmente, mas no momento em que o examinador diz 8 turistas em um barco e 7 em outro, devemos ignorar o resto. Esta foi a palavra final dele. Então, simplesmente analise.
Eu faço sem fórmula:
Maneiras distintas para escolher 8 turistas para um barco:
15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 = 6.435
8 7 6 5 4 3 2 1
Maneiras distintas para escolher 7 turistas no outro barco:7 x 6 x 5 x 4 x 3 x 2 x 1 = 0
7 6 5 4 3 2 1
Eu dividi por 8! e 7!, respectivamente, pois a ordem não importa. Isto é, João e Maria ou Maria e João no mesmo barco trata-se da mesma situação.
Para concluir:
(6.435 + 0) < (82 × 72)
6.435 < 3.136. ERRADO!
-
O enunciado diz que nenhum barco vai sair com menos de três pessoas logo a questão esta errada o Samuel esta certo!! Raciocínio lógico.
-
Analisando semanticamente a questão, os colegas teriam razão. Porém creio que a questão não deve se atentar a detalhes de interpretação de texto somente, portanto, quando se diz que "utilizará ... três barcos", o avaliador quis dizer que se atender a condição de ter pelo menos 3 ocupantes, os 3 barcos serão utilizados no passeio, caso contrário, somente os barcos que atenderem essa condição serão utilizados.
Compreendi bem a indagação e concordo que está semanticamente errado o enunciado, passível de anulação, porém analise a questão lógica para resolverem esse tipo de questão =D
-
concordo com os últimos comentários a questão é sim passível de anulação, ele pede que os barcos saiam com no minimo 3 ocupantes... e não se referem se eles sairão ou não ao mesmo tempo... ou seja, deixou a interpretação ambígua.
-
Questão certa. A quantidade de maneiras distintas de escolher é 0 e zero é inferior 8² x 7² uma vez que a questão diz que o grupo utilizará três barcos com no mínimo 3 turistas em cada. Não existe no caso maneiras válidas" Com base nessa situação hipotética " como pede a questão. Nesse caso pra entender o que esse cara quer tem que chamar um pai de santo.
-
Eu fiz assim:
C 15.8 = 6435
C 7.7= 0
Logo, 6435 é superior a 3136
-
C,S N,K= N !
/ K! x (N-K)!
N= 15 Turistas
K1 = 8 ocupantes barco azul e k2= 7 ocupantes barco amarelo
K1 = 8 (turistas ocupando o
barco azul )
C,S 15,8= 15! / 8! x (15-8)!
C,S 15,8= 15! / 8! x (7)!
C,S 15,8= 15x14x13x12x11x10x9x8x7x6x5x4x3x2x1 / 8! x (7)!
C,S 15,8= 15x14x13x12x11x10x9
/ 7x6x5x4x3x2x1
C,S 15,8= 6435
K2 (N=7 → Eram 15 turistas que
ocuparam 8 lugares no barco k1 , sobraram 7 turistas para ocuparem o barco k2)
Obs: Fatorial de zero =1
C,S 7,7= 7! / 7! x (7-7)!
C,S 7,7= 7! / 7! X 0!
C,S 7,7= 7! / 7! X 1 →7/7 =1
C,S 7,7 =1
Multiplicando as combinações:
C,S 15 ,8 x C,S 7,7 =
6435 x 1
C,S 15 ,8 x C,S 7,7 =
6435
E o enunciado afirma que as
combinações são inferiores a 82 x 72:
82 x 72 = 64 x 49 = 3136
C,S 15 ,8 x C,S 7,7 =
6435
Conclusão: Errada
A quantidade de maneiras
distintas é superior a 82 x 72, portanto a questão está
errada!
-
só queria dizer que escolher 7 entre 7 pra colocar no 2º barco só tem 1 jeito, e não 0, como vi nos comentários... cuidado pois uma bobagem dessa pode ser o caos, cansei de errar bobagem...
-
Aqui o problema pede apenas que utilizemos dois
barcos e não os três, o terceiro ficará no porto, logo com base nesse detalhe,
vamos dar prosseguimento na resolução da questão.
Como a ordem dos turistas nos barcos não é importante e
cada turista pode apenas ser escolhido apenas uma vez, usaremos Combinação
Simples:
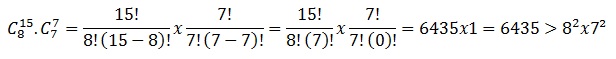
Obs.:
No primeiro barco entraram 8 de 15 turistas, logo para entrar no segundo,
restaram 7 turistas.
RESPOSTA: ERRADO
-
se tem que restar três no terceiro barco, dispensa-se qualquer tipo de cálculo além de 8+7=15.
-
Que isso gente.........quanta conta!!!!
No próprio enunciado diz q nenhum barco parte vazio!!!
Portanto se no azul tem 8 e no amarelo tem 7 é claro a quantidade de maneira NUNCA poderá ser esta!!!
Afinal a matéria é RACIOCÍNIO LOGICO
-
só uma observação, nandamslima (fernanda), neste caso, é obrigatório o uso dos parêntesis no denominador de 15! / 8! * 7!. Ou seja, o certo seria 15! / (8! * 7!). mas você fez as contas colocando o 7! no denominador, que é o certo. é só que alguém pode confundir e achar que o 7! está no numerador
-
que cacete, esse povo faz uma salada danada, amigos esqueçam o texto associado, vcs tem que saber interpretar, em nenhum momento a questao fez referencia, logo
escolher 8 turistas para ocupar o barco azul e 7 para ocupar o barco amarelo=
C 15, 8
C 7, 7
-
só esclarecendo para quem está reclamando de os barcos não saírem vazios.....
Em nenhum momento a questão diz que TODOS DEVEM SAIR.... ou seja... quem estiver com menos de 3 simplesmente não sai... PONTO... fim de papo...
Abraço...
-
ERRADO
-
Galera, pensei assim:
Total de pessoas =15
Quantidade de pessoas que quero colocar no barco = 8 no azul e 7 no amarelo
Se o meu total é diferente do que eu quero, ou é ARRANJO ou COMBINAÇÂO
Se eu colocar Pedro, João e Caio, é a mesma coisa de colocar Caio, Pedro e João, então a ordem não faz diferença = COMBINAÇÂO
C8,15 (barco azul) x C7x7 (barco amarelo)
FOCO, FORÇA e FÉ!
-
ERRADO
a primeira combinação já ultrapassa o valor da questão
C15,8 = 6.435
-
Um grupo de 15 turistas que planeja passear pelo rio São Francisco, no Canyon do Xingó, em Sergipe, utilizará, para o passeio, três barcos: um amarelo, um vermelho e um azul. Cada barco tem capacidade máxima para 8 ocupantes e nenhum deles deixará o porto com menos de 3 ocupantes.
ué, mas não tem que ter no mínimo 3 em cada barco?
-
A questão não fala sobre a possibilidade de um barco ficar no porto se tiver menos de 3 pessoas, mas fala que utilizará 3 barcos. Era um grupo fechado de 15 pessoas. Se iriam utilizar somente 2 barcos porque levaram 3 então?
Pra mim deveria ser anulada sem dúvida nenhuma.
Aí a pessoa não passa por uma questão na prova e a questão é essa. É pra ficar maluco.
-
Para o barco azul temos a C15,8 = 6435;
Para o barco amarelo temos a C7,7=1;
6435x1=6435
A questão trouxe 7² x 8² = 3136;
6435 > 3136
Questão errada.
-
Ao fazer a combinação de C15,8 e C7,7, Teremos o seguinte resultado:
15.14.13.12.11.10.09.08
_________________________= 13.11.5.9 (Simplificando)
08.07.06.05.04.03.02.01
07.06.05.04.03.02.01
______________________= 01
07.06.05.04.03.02.01
13x11x5x9 (>) 8x8x7x7
Combinação de C(n,0)=1
Combinação de C(n,1)=n
Combinação de C(n,n)=1
-
G-E
Não é necessário realizar cálculos complexos.
Primeiro barco ~> C15,8 = 15x14x13x12x11x10x9x8 / 8x7x6x5x4x3x2x1 = 13x11x5x9 (após simplificar)
Segundo barco ~> C7,7 = 1
Logo, 13x11x5x9 > 8x8x7x7
Obs: Na maioria das vezes, o CESPE escolhe uma assertiva que afirme um valor próximo do resultado. Porém, não será assim 100% das vezes.