-
Resolvi desta forma: Dentro do grupo de 5 pessoas que serão selecionadas temos:
20 possibilidades distintas de Homens, já que no total são 20 servidores homens.
210 maneiras distintas de seleção das 4 mulheres que farão parte do grupo. Como temos um total de 10 mulheres, e deste, serão selecionadas apenas 4, usamos a formula de Combinação, já que a ordem de seleção não importa. C 10,4= 10!/ 4! 6! = 210
Agora multiplica-se as 20 possibilidades de homens X 210 de mulheres = 4200. Portanto, gabarito errado!
-
RESOLUÇÃO:
Temos um total de 30 servidores, sendo 10 mulheres e 20 homens.
Queremos escolher exatamente 4 das 10 mulheres e 1 dos 20 homens para formar
um grupo.
Repare que a ordem de escolha das mulheres ou dos homens é irrelevante
para a nossa análise. Escolher as mulheres Andressa, Bia, Clara e Daiane, nesta
ordem, é o mesmo que escolher primeiro a Bia, depois a Daiane, depois a Andressa
e por fim a Clara – afinal o grupo continuará sendo composto pelas mesmas 4
mulheres. Da mesma forma, também é irrelevante escolher o único homem antes de
escolher as mulheres, depois de escolher as mulheres ou entre as escolhas das
mulheres. Em qualquer caso, o grupo será composto por aquele homem escolhido e
as 4 mulheres escolhidas.
Quando a ordem de escolha é irrelevante, basta utilizarmos a fórmula da
combinação para saber o número de grupos a serem formados.
Começamos escolhendo 4 das 10 mulheres, o que é feito através da
combinação das 10 mulheres em grupos de 4, ou seja:
C (10,4) = 10 9 8 7 / 4!
C (10,4) = 210 possibilidades
Já para a escolha do único homem temos 20 possibilidades (qualquer um dos
20 disponíveis).
Portanto, temos 210 possibilidades para a escolha das mulheres e 20
possibilidades para a escolha do homem. Repare que a escolha das mulheres é
independente da escolha dos homens. Quando temos eventos independentes e
sucessivos (devemos escolher as mulheres E escolher o homem), o total de casos é
dado pela multiplicação das possibilidades:
Nº de formas de escolher 4 mulheres e 1 homem = 210 x 20
Nº de formas de escolher 4 mulheres e 1 homem = 4200
Fonte: https://d3pt2alc3jyv7g.cloudfront.net/49019/00000000000/curso-4892-aula-00-v1.pdf?Expires=1411672795&Signature=ZTLQOb6R9Ev-f96-d0liqgOL-~Hi5QhRjWWAIT8~pazeriFFLnR6-TNZnpvVnRsnP~PNdJniW-LjBtPSO0cLD-Jqg6nGDFGTSOIqquI1lJad7pLhwoiQr2MwgYvfitSYtfG87hLtmIe47l7a8Cu1Jijn1YCpluBiT1VyY4e5AJo_&Key-Pair-Id=APKAIKHUAVWTIL5FVANA
-
Simplificando,
C10,4 x C20,1: 4200
4200>4000
-
Servidores = 30
Homens = 20
Mulheres = 10
para selecionar 5 sendo 4 mulheres
C10,4 x C20,1 = 4.200
-
Como 10 dos 30 servidores são do
sexo feminino, restam 20 servidores do sexo masculino. Queremos saber a quantidade
de maneiras distintas de se selecionar 5 servidores dessa repartição de forma
que 4 sejam do sexo feminino, assim:
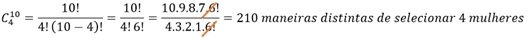
Multiplicando agora o resultado
acima pela quantidade de funcionários homens (possibilidades que seja do sexo
masculino): 210 x 20 = 4200.
Logo, a
quantidade de maneiras distintas de se selecionar 5 servidores dessa repartição
de forma que 4 sejam do sexo feminino é superior
a 4.000.
Resposta:
Errado.
-
Servidores: 30
Homens: 20
Mulheres: 10
Selecionar 5 servidores, sendo 4 mulheres
C10,4 x C20,1 = 210.20 = 4.200
-
Pessoal, fiquei com uma dúvida! Pensei na seguinte possibilidade...
"A quantidade de maneiras distintas de se selecionar 5 servidores dessa repartição de forma que 4 sejam do sexo feminino é inferior a 4.000."
Esses 4 servidores do sexo feminino são exatamente 4 ou poderá haver grupos com 5 servidores do sexo feminino? Pois se assim for acredito que o cálculo seria diferente.Os 20 homens seriam somados ao restante de mulheres que não ficou fixo no grupo. Sobrariam 6, sendo 20 homens + 6 mulheres. Poderia ser C10,4 x 26 ?
Se alguém puder ajudar, agradeço!
-
Cuidado Carlos o enunciado é TAXATIVO, ou seja, são 4 do sexo feminino.
-
realmente o CESPE nao quer saber se vc aprendeu matematica ou se deu sorte em acertar a questao...pq todas as questoes sao inumeras respostas diferentes, onde tds acertaram a questao e continuamos sem saber se a resolução certa foi minha ou sua...
Resolvi dessa maneira...
10 x 9 x 8 x 7(mulheres) 20(homens) = 5.040
-
GABARITO (ERRADO)
Dizer que quer 4 mulheres nos 5 servidores, já se pode deduzir que só haverá um homem, logo é a combinação de 20,1 ou 20 vezes o que der na combinação das mulheres C10,4 que dá 210, agora 210 x 20 =4200
-
Paula Arnaud a questão diz: maneiras distintas. Tem que usar a regra de combinação. Se a questão pedisse quantas maneiras possíveis você poderia resolver da maneira que vc fez.
-
A quantidade de maneiras distintas de se selecionar 5 servidores dessa
repartição de forma que 4 sejam do sexo feminino é inferior a 4.000.
(ERRADA).
"realmente o CESPE nao quer saber se vc aprendeu matematica ou se deu
sorte em acertar a questao...pq todas as questoes sao inumeras respostas
diferentes, onde tds acertaram a questao e continuamos sem saber se a
resolução certa foi minha ou sua...
Resolvi dessa maneira..."
"10 x 9 x 8 x 7(mulheres) 20(homens) = 5.040"
Paula Arnaud, para calcular uma combinação sem utilizar a fórmula Cn,p=n!/(n-p)!, deve-se utilizar a multiplicação como você fez, contudo para retirar os agrupamentos que se repetem, deve-se dividir a multiplicação pelo fatorial da quantidade de espaços utilizados:
Quantidade de maneiras distintas de selecionar as 4 mulheres:
n (total)=10 mulheres
p(mulheres que serão selecionada) =4
10x9x8x7 / 4x3x2x1 = 210 maneiras distintas
Quantidade de maneiras distintas de selecionar 1 homem:
n( total)= 20 homens (30 - 10 mulheres)
p( homens que serão selecionados) = 1 homem
20/1= 20 maneiras distintas.
4 servidores devem ser do sexo feminino (210 maneiras distintas) E 1 deve ser do sexo masculino (20 maneiras distintas) . ("E" princípio multiplicativo).
210 x 20 = 4.200 maneiras distintas de serem selecionados os 5 servidores.
-
Cuidado! A solução da questão não é 10 x 9 x8 x7 = 5.040!
Isso seria para fazer uma "senha" com as mulheres de modo que a ordem de sua escolha fizesse diferença.
Como não faz, tem que se usar a fórmula da Combinação:
C((10,4)) = 210
Depois multiplicar por 20, para aquela única vaga para um homem. 210 x 20 = 4.200
TOTAL 4.200
-
Eu resolvi pensando que poderiam ser 4 mulheres e 1 homem OU 5 mulheres, teria-se, assim no minimo 4 mulheres formando a comissão de 5 pessoas. Logo:
C10,4 e C20,1 (4 mulheres e 1 homem) OU C10,5 (5 mulheres) =
(10x9x8x7/4x3x2x1 + 20 ) + (10x9x8x7x6/5x4x3x2x1) = 4200 + 252 = 4452.
-
Adriana, cuidado... O enunciado pede a quantidade de maneiras distintas de se selecionar 5 servidores dessa repartição de forma que 4 sejam do sexo feminino, e não que sejam NO MÍNIMO 4 mulheres....
Acredito que a resposta seja 4200 maneiras.
-
Fiz assim:
5 servidores: 4 mulheres e 1 homem.
C10,4 e C30,1 ( obs.: "e" multiplica, "ou" soma).
C10,4 = 10!/4!.6! = 10.9.8.7.6/4.3.2.6! = 210
C30,1 = 30!/1!.29! = 30.29!/29! = 30
logo, 210x30 = 6300
-
Resolvi por Combinação.
São 30 servidores, 10 do sexo feminino e 20 do sexo masculino.
A questão pede a quantidade de maneiras distintas de se selecionar 5 servidores dessa repartição de forma que 4 sejam do sexo feminino é inferior a 4.000.
ou seja C10,4 = 210 x C20,1 = 20
210 x 20 = 4.200
GAB: ERRADO
=]
-
C 10,4=210
C 20,1=20
210*20=4200
GABARITO: ERRADO
-
Sem pensar em fórmulas, temos:
30 servidores: 10 mulheres e 20 homens
5 servidores
10 X 9 X 8 X 7
________________ = 210 x 20 que é o último espaço = 4320
4 X 3 X 2 X 1
Obs: Sempre que pedir distinto, tem que dividir embaixo pelo número de casas
-
melhor resposta do Gabriel Antunes ;....
-
10x9x8x7 Número de possibilidades com as mulheres. Agora multiplica pelo número de possibilidades de escolher homens, são 20, 4x3x2x1 escolher qualquer um, então 210x20 que dá 4200
-
É uma combinação GLR, só que feita com atenção:
1º descobrir a quantidade de maneira de ser MULHER, temos então: C(10,4)=210
2º se 10 de 30 são mulheres, é sinal que 20 que restam são homens, e se 4 de 5 são mulheres, apenas 1 é homem, logo, temos outra combinação:
C(20,1)=20
3º como tudo é formado por HOMENS E MULHERES, esse E quer dizer que iremos MULTIPLICAR, logo:
210.20=4200
GAB: ERRADO
-
nos 15 minutos do vídeo mostra a resolução, resposta 4200 feito por combinação;
https://www.youtube.com/watch?v=ODGJkco3f2U
-
São 30 pessoas (10 mulheres e 20 homens) e quero montar um grupo de 5 pessoas, sendo 4 mulheres e 1 homem.
C10,4 x C20,1 = 4200
Gab. ERRADO
-
Por que 210 X 20 ? a questão não deixa claro. Pode ser homem, ou mulher como último membro, a questão não diz que tem ser um homem, ao meu ver pode tanto ser homem ou mulher, o que ela pede é que tenha 4 mulheres na comissão esse cálculo tinha que ser 210 x 26, acertei mas por sorte.
-
GABARITO: ERRADO
30 servidores → 10 mulheres e 20 homens
Combinações de 4 mulheres
C10,4 = 10! / 4! 6!
C10,4 = 210
Combinação de 1 homem
C20,1 = 20
Maneiras de selecionar 5 servidores
210 x 20 = 4200 > 4000
-
Total: 30 servidores
Feminino: 10
Masculino: 20
Fem:
C10,4
Masc:
C20,1
210 x 20 = 4200
-
C 20,1 x C 10,4 = 20 x 210 = 4200
-
ADOTE :
M= masculino
F= feminino
F=10
M=20
A EQUIPE DEVE SER FORMADA POR : 4 FEMNINA e 1 MASCULINO
FFFFM
devemos fazer combinação:
para feminino : 10,4 =210
para masculino: 20,1=20
AGORA BASTA MUTIPLICAR 210x20=4.2000
-
Gab: Errado
Total de mulheres: 10
Total de homens: 20
Vagas para mulheres: 4
Vagas para homens: 1
Mulheres: C10,4 = 210
Homens: C20,1 = 20
Como são homens E mulheres, multiplicamos: 210 x 20 = 4200
-
Minha contribuição.
Começamos escolhendo 4 das 10 mulheres, o que é feito através da combinação das 10 mulheres em grupos de 4, ou seja:
C(10,4) = 210 possibilidades
Já para a escolha do único homem temos 20 possibilidades (qualquer um dos 20 disponíveis). Portanto, temos 210 possibilidades para a escolha das mulheres e 20 possibilidades para a escolha do homem. Repare que a escolha das mulheres é independente da escolha dos homens. Quando temos eventos independentes e sucessivos (devemos escolher as mulheres E escolher o homem), o total de casos é dado pela multiplicação das possibilidades:
Nº de formas de escolher 4 mulheres e 1 homem = 210 x 20
Nº de formas de escolher 4 mulheres e 1 homem = 4200
Note que o item está ERRADO, pois o total é superior a 4000 (como costuma acontecer nas questões do CESPE, encontramos um número próximo àquele presente no enunciado).
Resposta: E
Fonte: Direção
Abraço!!!