-
O segredo da questão está na palavra "necessariamente", ou seja, todas as vezes que vc fizer o cálculo vai dar um número inteiro par. Gabarito E.
-
Lembrando que no caso (a) de Arthur, se fosse 12 + 18 (dois número pares) / 2 daria 15, logo não teríamos um número inteiro par.
Por isso, gabarito = "e"
-
não entendi, e como eu faço? eu tenho que testar todos os númeroes pares e testar todos? como pode isso ?? tipo 2+2, 40+40...ñ entendi nada.
-
Tem que testar as sugestões dos alunos procurando por, pelo menos, um exemplo que dê errado.Ex:
Arthur -> (2+4) / 2 = 3. Não é par
Bernardo -> (5+10) /2 = 7.5 Não é par
Carlos -> (4+9)/2 = 6.5 Não é par
Davi -> (2+3+4)/3 = 3 Não é par
Edu -> Todas as possibilidades resultam número par. Reposta: Letra E
-
Não consegui identificar uma resolução possível para essa questão....
-
Não consegui identificar uma resolução possível para essa questão....
-
Só pensar que qualquer múltiplo de 4 quando dividido por 2 será necessariamente par.
-
Testando cada alternativa:
a) Arthur escolheu a média entre dois números pares;
(ERRADO)
É sabido que 2n e 2n + 2, com n = 1, 2, 3, 4, ....
sempre serão números pares, assim:
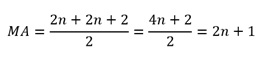
Onde 2n + 1 é um número ímpar para n = 1, 2, 3, 4,
....
b) Bernardo escolheu a média entre dois múltiplos de
5; (ERRADO)
Para ser um número múltiplo de 5, basta o número
ser terminado por 0 ou 5, adotando um exemplo qualquer: MA = 5 + 10 / 2 = 15 /
2 = 7,5.
c) Carlos escolheu a média entre dois números
quadrados perfeitos; (ERRADO)
Fazendo
um contra exemplo: MA = 9 + 16 / 2 = 25 / 2 = 12,5.
d) Davi escolheu a média entre três números
consecutivos; (ERRADO)
Seja
n, n+1, n+2 números consecutivos para n = 1, 2, 3, 4, ... temos:
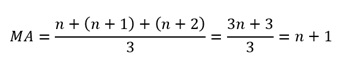
Onde n + 1 pode um número par ou ímpar para n = 1,
2, 3, 4, ....
e) Edu escolheu a média entre dois múltiplos de 4. (CERTO)
Calculando a média para dois números múltiplos de
4:
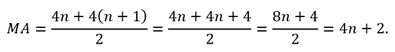
Onde
4n + 2 sempre será um número par para n = 1, 2, 3, 4, ....
RESPOSTA: (E)
-
Gustavo Miranda, muito obrigada!
-
vcs viram a explicação do professor????...ele pensa que nós somos o que, estudantes de física?????....e ele não é o nosso prof titular de raciocinio, o nosso 'show de bola'....o nosso 'show de bola' nao iria fazer isso conosco, 'os seus aluninhos'....figurassa esse profi 'show de bola'....eu apelidei ele assim.....hehehe....'altos profi´s...'
-
Testando é mais fácil, mas para os que gostam de demonstrações, vamos lá:
Artur: M = (2.k+2.y)/2 = k+y => sendo k e y números inteiros quaisquer, é fácil perceber que há resultados pares e ímpares. Obs: Número par é um número múltiplo de 2, ex: 2.k. Logo, não ganhou.
Bernardo: M = (5.k+5.y)/2 = 2,5.(x+y) => sendo k e y números quaisquer, fica fácil perceber que há resultados não inteiros. Logo, não ganhou.
Carlos: M = (a² + b²)/2 => sendo a e b números quaisquer inteiros, é fácil notar que quando ambos forem par ou ímpar o resultado será par, porém, caso um seja par e o outro ímpar, a divisão não será inteira. Logo, não ganhou.
Davi: M = [k + (k+1) + (k+2)]/3 = (3.k +3)/3 = 3.(k+1)/3 = k+1, ou seja, é um número que pode ser par ou ímpar. Logo, não ganhou.
Edu: M = (4.k + 4.y)/2 = 4.(k+y)/2 = 2.(k+y), isto é, trata-se de um múltiplo de 2 e, portanto, será, necessariamente, inteiro par, independente de x e y. Logo, teve a nota aumentada.
Gabarito: E.