SóProvas

ID
131968
Banca
FGV
Órgão
CAERN
Ano
2010
Provas
Disciplina
Raciocínio Lógico
Assuntos

Cinco máquinas com a mesma capacidade de trabalho enchem 30 garrafas de 250 mL em 12 minutos. Três dessas máquinas serão utilizadas para encher 15 garrafas de 500 mL. Para realizar essa tarefa, serão necessários

Alternativas
Comentários
  • 15 garrafas de 500ml=30 de 250mlMáquinas____Garrafas 250 ml_____Tempo min.5_______________30_________________123_______________30_________________xQuanto mais Tempo mais Garrafas (diretamente proporcionais)Quanto mais Tempo menos Máquinas (Inversamente proporcionais)12/x=30/30 x 3/512/x=90/150x=20 minutosGabarito (c)
  • você deve analisar cada grandeza separadamente com a grandeza onde se encontra a icognita "x". Se aumentar ou diminuir uma grandeza e aumentar ou diminuir a outra respectivamente, as grandezas serão diretamente proporcinais, se aumentando uma grandeza e diminuindo a outra, ou vice-versa, as grandezas serão iversamente proporcionais.

    máquinas ----- garrafas ----- ml ----- minutos
    .... 5 ............. 30 ........ 250 ....... 12
    .... 3 ............. 15 ........ 500 ........ x

    máquinas: se diminui o nº de máquinas, aumentam os minutos (inversamente proporcional)
    garrafas: menos garrafa, menos minutos (diretamente proporcional) 
    ml: mais mL, mais minutos (diretamente proporcional)

    Então teremos:

    \frac{12}{x} = \frac{3}{5} \times \frac{30}{15} \times \frac{250}{500} \\ \frac{12}{x} = \frac{3 \cdot 2 \cdot1}{5\cdot 1 \cdot 2} \\ \frac{12}{x} =\frac{6}{10}

    6x = 120 \Right x = \frac{120}{6} = 20

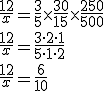
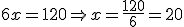
    RESPOSTA: "C" 20 minutos

  • Não entendi de onde saiu o 30/30 x 3/512?

  • Primeira Coisa que verificamos é que a quantidade de ML são iguais.

    30 garrafas x 250ml = 7.500 ml

    15 garrafas x 500ml = 7.500 ml... 

    Logo não devemos nos preocupar com a quantidade de ML.

    Vamos apenas focar nas maquinas e tempo de enchimento.

    Então se: 5 maquinas enchem em 12 mim ... 3 maquina vão encher em quanto?

    5 ----- 12

    3 ---- x   (Grandeza Inversamente proporcional) - 3 maquinas vão demorar mais pra encher do que 5 maquinas.

    Logo:

    5 --- x                      =               5 x 12 / 3 = 20 minutos.

    3 --- 12



  • Utilizo esse método para regra de 3 composta.


    MQ          GARRAFAS                ML             TEMPO


    5+                 30                      250               12

    3                   15 -                     500 +             X


    X = 12 * 500 * 15 * 5 / 250 * 30 * 3

    X = 300 / 15

    X = 20

  • Usei essa lógica

    5 máq = 30 garrafas de 250 ml em 12 min

    1 máq = 6 (30/5) garrafas de 250ml em 12 min

    1 máq = 3 (6/2 - duas garrafas de 250ml equivalem a 1 de 500ml) garrafas de 500ml em 12 min

    1 máquina = 1 garrafa de 500 ml em 4 min (12 / 3 garrafas produzidas no tempo)

    3 máquinas = 3 garrafas de 500 ml em 4 min (um ciclo de produção)

    15 (total a ser produzido) / 3 (produção de cada uma das três máquinas por ciclo) = 5 ciclos de produção

    Assim, 3 máquinas = 15 garrafas de 500 ml em 20 min (4 min por ciclo * 5 ciclos)


  • Aqui temos:

    Máquinas                             Volume                          Tempo

    5                                            30 x 250                             12

    3                                            15 x 500                              T

    Quanto MAIS tempo disponível, MENOS máquinas são necessárias, e MAIS volume pode ser produzido. Assim, devemos inverter a coluna das máquinas:

    Máquinas                           Volume                            Tempo

    3                                             7500                                   12

    5                                            7500                                    T

    Montando a proporção:

    T = 20 minutos