-
Acho que o gabarito está equivocado. A questão deve ser resolvida da seguinte forma:
Raiz1 = 4, logo
Raiz2 = 4³ + 4² + k4 = 0 ... 64 + 16 + k4 = 0 ... 80 + k4 = 0 ... k4 = -80 ... k = -80/4 ... k = -20
Raiz3 = 0, logo 0³ + 0² + (-20)*0 = 0
Resposta Alternativa (A) -20, 0
-
O gabarito está correto. -20 não é raíz é valor de k. Pra resolver é necessário por x em evidência. Uma das raízes será zero. A equação de segundo grau gerada após colocar x em evidencia tem raizes -5 e 4. Cuidado pra não marcarem a "d". Fiquei tão eufórica com a resposta que marquei errado ><
-
Ola galera do QC este exercício resolvi da seguinte modo, como o exercício narra que uma das raízes é 4 então substitui esse numero nas incógnita e encontrei o seguinte resultado:
X3+x2+kx=0 e colocando em evidencias temos: vou chamar d de delta
(4)3+(4)2+k4=0 x[x2+x+(-20)]=0 então x=0 ou x"=-1-9
64+16+k4=0 x2+x-20=0 x'=-1+9 2
k=-80/4 d=b2-4ac. 2 x'=-10/2=-5
k=-20 d=(1)2-4(1).(-20) x'=8/2=4 Alternativa B
d=1+80 = 81
x= -1-ou+ raiz de 81
2a
x= -1-ou+9
2a
-
Como uma das raízes da equação é 4, basta substituirmos este valor em "x" para encontrarmos k, assim:
f(4) = 4³ + 4² + 4k = 0
64 + 16 + 4k = 0
4k = -80
k = -80/4
k = -20
Assim, f(x) = x3 + x2 - 20x = 0
Colocando o "x" em evidência:
x(x² + x - 20) = 0
Então x = 0 e x² + x - 20 = 0
Ou seja uma das raízes é x = 0. Resolvendo a equação x² + x - 20 = 0 pela fórmula de Bhaskara:
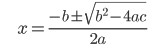
Encontraremos as outras duas raízes, x = 4 e x = - 5.
Resposta: Alternativa B.
-
Fiz da seguinte forma,o comando apresentou a raiz 4,logo podemos utilizar o método de Briot-Ruffini para abaixar para 2 o grau da equação. Ficando x²+5x= 0,que possui raízes 0 e -5.
-
Como o amigo abaixo disse, resolvendo pelo algaritimo de Briot-Ruffini (pesquise sobre é bem simples) isso sai rápido
Como uma das raízes é x' = 4
conseguimos determinar o valor de K substituindo os X da esquação x³ + x² + kx = 0
chegando em k = -20
Com a equação reduzida por briot-ruffini temos
x² + 5x = 0
resolvendo a equação
x' = 0 e x'' = -5
Gabarito letra B
Bons estudos galera
-
Nem precisa usar Briot-Ruffini. Coloca x em evidencia e temos:
x(x^2 + x - 20) = 0 ; para K = - 20
x`= 4; x" = 0 sobra como opção de resposta -5, -20 e 20. Não pode ser nem 20 e nem -20 pois os valores são baixos, restando como opção apenas -5. Agora é só substitui na equação e testar:
(-5)^2 - 5 -20 = 0 ==> 25 - 25 = 0; então as raizes são x' = 0; x'' = 4 e x''' = -5 . Letra B.
-
https://www.youtube.com/watch?v=JA70CIj8zTA
-
É só usar as relações de Girard, galera!
Soma das raízes:
x1 + x2 + x3 = -b/a
4 + x2 + x3 = -1
x2 + x3 = -5
A única alternativa que a soma das outras raízes da -5 é a alternativa B
GABARITO: LETRA B