-
A negação de uma sentença cujo operador lógico é o se e somente se, se faz pela troca do operador condicional, pela disjunção exclusiva, OU...OU, mantendo a frase íntegra.
Ex.: ~(A se e somente se B) = OU A OU B.
~(A <---> B) = (v A v B).
Logo, a resposta apresentada está incorreta.
Me parece que a resposta mais adequada seria a letra C, uma vez que ~[p ∨ ~a(p ∧ q)] = ~p ∧ a(~p v ~q).
considerando a tabela verdade da conjunção e da disjunção inclusiva, percebe-se que são falsas!
-
Concordo, Erikson
Na (b), a segunda proposição não é a negação da primeira, mas é logicamente equivalente!
-
p q p^q ~(p^q) p v ~(p^q) ~[p v ~(p^q)]
v v v f v f
v f f v v f
f v f v v f
f f f v v f
Resposta correta: Letra C
-
Mas por que a D esta errada? A equivalente da condicional não é negar a primeira e manter a segunda?
-
Barbara Engelmann, mater a segunda porém com o conectivo "ou". Na questão o conectivo é o "e".
-
A proposição ~[p ∨ ~(p ∧ q)] é logicamente falsa, pois a NEGAÇÃO de "ou" é o "e", e a NEGAÇÃO de "e" é o "ou"; e quando eu tenho "E" a lógica SÓ será VERDADEIRA, se AMBAS FOREM VERDADEIRAS, vejamos:
~[p ∨ ~(p ∧ q)] = ~p ∧ (p ∧ q)
Considerando a segunda parte da proposição, (p ∧ q) = P e Q, só poderá ter lógica VERDADEIRA se p=V e q=V. Se p é V então ~p é FALSO. Daí [~p ∧ (p ∧ q)], ficaria [F e (V e V)] = F e V; tendo o "e", só seria verdadeiro se ambos fossem verdadeiros, sendo assim a PROPOSIÇÃO É LOGICAMENTE FALSA!!!!
-
Testando cada alternativa até encontrar a verdadeira:
A) Errado.
Comentário: Desenvolvendo a proposição ~(p ∧ q) pela lei de Morgan, vemos que realmente ela é igual a ~p v ~q, então ~(p ∧ q) = (~p ∨ ~ q), logo, são logicamente equivalentes.
B) Errado.
Comentário: Negando a proposição “Ele faz caminhada se, e somente se, o tempo está bom", teríamos:
Ou ele faz a caminhada, ou o tempo está bom
C) Certo.
Comentário: Desenvolvendo a proposição ~[p ∨ ~(p ∧ q)] pela lei de Morgan:
~[p ∨ ~(p ∧ q)] = ~[p ∨ ~p ∨ ~q] = ~p ∧ p ∧ q
Fazendo a tabela verdade:
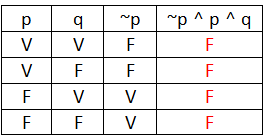
Logo a a proposição ~[p ∨ ~(p ∧ q)] é logicamente
falsa.
Resposta: Alternativa C.
-
BOA QUESTÃO....
ACERTAMOS GALERA!!!!
-
questão inteligente....
-
Fiz da seguinte maneira: Negar [PV¬(∧Q)] =====> ¬P ∧¬¬(P ∧Q)=====> ¬P ∧¬(¬PV¬Q)======RESULTADO APÓS TRANSFORMAÇÕES ¬P ∧ (P∧Q) AGORA FAZEMOS A TABELA VERDADE DE CADA ELEMENTO
P | Q | ¬P | P ∧Q | ¬P ∧(P∧Q)
V | V | F | V | F
V | F | F | F | F
F | V | V | F | F
F | F | V | F | F
-
Vamos aos erros de cada item:
a) As proposições ~(p ∧ q) e (~p ∨ ~ q) não são logicamente equivalentes.
ERRADA: (~p v ~q) é a negação de (p ^ q);
b) A negação da proposição “Ele faz caminhada se, e somente se, o tempo está bom", é a proposição “Ele não faz caminhada se, e somente se, o tempo não está bom".
-> ERRADA: a negação seria "Ou ele faz caminhada, ou o tempo está bom";
c) A proposição ~[p ∨ ~(p ∧ q)] é logicamente falsa.
-> CORRETA;
d) A proposição “Se está quente, ele usa camiseta", é logicamente equivalente à proposição “Não está quente e ele usa camiseta".
-> ERRADA: seria equivalente as seguintes proposições: "Se ele não usa camiseta, então não está quente" / "Não está quente ou ele usa camiseta"
e) A proposição “Se a Terra é quadrada, então a Lua é triangular" é falsa.
-> ERRADA: não tem como saber se é verdadeira ou falsa.
Acredito que seja isto.
Foco, força e fé!
-
Concordo da letra C estar correta, mas não entendi a letra A estar errada. Se uma é a negação da outra, então elas realmente não são equivalentes. O que ser equivalente tem a ver com negação?
Alguém me explica? :(
-
Gab: "C"
Fracielle Oliveira, na alternativa "A" uma não é a negaçao da outra, pelo contrário uma é a equivalêcia lógica da outra e a acertiva fala que não são equivalentes por isso está incorreta veja:
aqui foi usado a lei de morgan que se resume em negar tudo que está dentro do parenteses, lembrando que a negaçao do v é o ^ e vice versa. Obseve que negar tudo que esta dentro do parentese é o mesmo que negar um por um, por isso são equeivalentes.
a)As proposições ~(p ∧ q) e (~p ∨ ~ q) não são logicamente equivalentes.(Errado)
Bons estudos! Espero ter ajudado.
-
Gente, a letra A está incorreta porque a questão fala que as proposições não são equivalentes, mas o são . Ao montar a tabela verdade veremos que o resultado é o mesmo em ambas as proposições, qual seja: F V V V .
-
Qual o erro da letra E?
-
Vamos avaliar cada alternativa:
a) A proposição “Se está quente, ele usa camiseta” é logicamente equivalente à proposição “Não está quente e ele usa camiseta”.
Sendo p = “está quente” e q = “usa camiseta”, temos:
p
q
~p e q
Sabemos que pq é equivalente a “~p ou q”, mas não a “~p e q”. Veja que se tivermos p e q Verdadeiras, teríamos pq com valor lógico V e “~p e q” com valor lógico F. Item FALSO.
b) A proposição “Se a Terra é quadrada, então a Lua é triangular” é falsa.
Aqui devemos apelar aos nossos conhecimentos para afirmar que “Terra é quadrada” e “Lua é triangular” são duas informações incorretas, isto é, Falsas. Mas, em uma condicional, FF tem valor lógico verdadeiro, ao contrário do que afirma este item. Item FALSO.
c) As proposições 
e 
não são logicamente equivalentes
Sabemos que a negação da conjunção 
, isto é, 
, é justamente a disjunção 
. Portanto, é correto falar que 
é equivalente a 
, ao contrário do que o item afirma. Item FALSO.
d) A negação da proposição “Ele faz caminhada se, e somente se, o tempo está bom”, é a proposição “Ele não faz caminhada se, e somente se, o tempo não está bom”.
Sabemos que a negação de uma bicondicional (“se e somente se”) é feita com um “ou exclusivo” (“ou..., ou...”). Item FALSO.
e) A proposição 
é logicamente falsa.
Vejamos a tabela-verdade desta proposição:
De fato, temos uma contradição, isto é, uma proposição que somente possui valor lógico F. Item VERDADEIRO.
Resposta: E
-
A proposição da alternativa E é verdadeira pois o antecedente é falso e o consequente é falso (FF), então a condicional é verdadeira, ela está incorreta porque a banca diz que ela é falsa. Para uma condicional ser falsa, é preciso que o antecedente e o consequente sejam (VF) nessa ordem.