-
Letra A
a) CERTO
O número de candidatos que são físicos, biólogos ou químicos é dado pela
soma das regiões no diagrama: 33+15+8+24+24+8+50 = 162. Portanto, os
candidatos que não tem nenhuma dessas formações são 250 – 162 = 88.
b) Errado. São 33.
c) Errado. São 24.
d) Errado. São 24.
e) Errado. Temos 15 candidatos com essas duas formações apenas, em um total de
250. A probabilidade de selecionar um desses 15 é de 15/250 = 0,06 = 6%.
-
NÃO ENTENDI A AFIRMAÇÃO DA LETRA ''A''
SE ALGUÉM CONSEGUIR DAR UMA EXPLICAÇÃO?
POR QUE TENTEI SEGUIR OS DADOS DO "FERNANDO" E NÃO ENTENDI DA ONDE SAIU AQUELES NÚMEROS...
-
Uma outra forma que é parecida com a do Fernando é:
Soma-se as quantidades de formados em cada curso (80+90+55), subtrai-se dos formados que possuem dois cursos (32+23+16) e soma-se com os que são formados nos 3 cursos (08). O resultado subtrai-se do total de candidatos (250), conforme abaixo:
X= Quantidade de candidatos que não são formados em Física, Química e Biologia, então:
Total F+ B + Q - ( B,F)(Q,F)(B,Q) + (F,Q,B)
| | | | | | | |
X = 250 - {(80+90+55) - ( 32 + 23 + 16) + 08}
X = 250 - {(225 - 71) + 08}
X = 250 - {154 +8}
X = 250 - 162
X - 88.
-
Primeiro vamos achar os que sao apenas uma formaçao:
Física: 80-(23+32-8)=33
Biologia: 90-(32+16-8)=50
Química: 55-(23+16-8)= 24
Agora acha os que têm apenas duas formações:
F+Q=23-8=15
Q+B=16-8=8
F+B=32-8=24
As três formações: 8
Agora soma todos:
33+50+24+15+8+24+8= 162
250-162=88
Ou seja 88 sem essas três formações, fazendo assim confirma o erro das outras questões.
Gab. A
-
Como a solução pode ser somar os valores dentro do diagrama e esses valores darem diferentes da soma dos valores totais dados no enunciado do problema?
80 físicos
90 biólogos
55 químicos
225 total subtraindo-se dos 250 candidatos = 25 pessoas que não são formadas em nenhuma disciplina informada...
E não 88...
Se não convenci, pergunto: aquele que é formado em física e biologia conta como duas pessoas?? Porque ele Pergunta pelo número de candidatos e não pelo número de diplomas....
Para a mim, não tem resposta correta!
-
THAYNARA a alternativa A diz , mais de 80 dos candidatos selecionados NÃO são físicos e nem biólogos e nem químicos.
Logo, você vai somar todos os resultados que obtiver "nas bolinhas" da teoria de conjunto: Física e Biologia e Química, ficando 33+50+24+15+8+24+8= 162. Subtrai o valor encontrado pelo total, 250-162=88
88 candidatos selecionados ao cargo de perito criminal não são formados nessas áreas.
Igual a Andressa Castro explicou.
.
KiConcurseiro, a soma dos valores já foram subtraídos na medida que foi montando "as bolinhas", logo não tem pessoa e nem diploma sendo contado duas vezes. Você tá somando o total de Físicos, Biólogos e Químicos, tá errado.
Dentro do total de Físicos (80), existem pessoas que são formadas em Biologia e Física (32), pessoas formadas em Química e Física (23) e pessoas formadas em Física, em Química e em Biologia (8), como diz o enunciado da questão. Mas quando subtrai todas essas intersecção, fica 33 a quantidade de pessoas formadas somente em Física. Daí, vai fazendo isso pra todos.
Somente Químico (24)
Somente Biólogo (50)
Espero ter ajudado, bons estudos (:
-
KiConcurseiro Sua SOMA não é lógica.
Note que 80+90+55 não significa que são 225 pessoas... Pois os 80 podem está dentro dos 90... assim como alguns dos 55 podem esta nos 90....
Exemplo:
Somos 3 indivíduos.
Um é Físico e Químico
Outro é Químico e Biólogo
Outro é Físico e Biólogo
Eu posso dizer que há
2 Físicos
2 químicos
2 biólogos
E nao são 6 pessoas... são apenas três.
Se não conseguir entender precisará de um exemplo prático.
-
Olá pessoal,
Vejam a resolução dessa questão no vídeo que gravei abaixo:
https://youtu.be/hKhYLxX0SZs
Alternativa correta letra A
-
Vocês são muito legais, tirando as dúvidas, tentando ensinar mesmo. Parabéns a todos que deram um pouquinho do seu tempo.
-
Fazendo o diagrama de Venn:
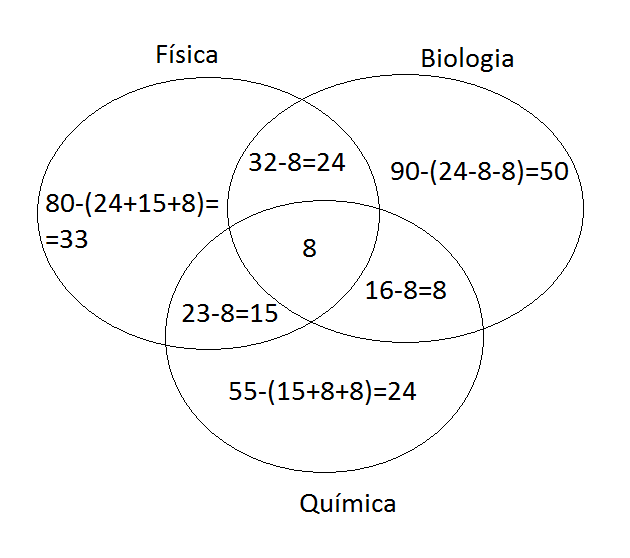Somando tudo: 33 + 24 + 50 + 8 + 24 + 15 + 8 = 162. Subtraindo do total de 250 participantes:
250 - 162 = 88
Assim, de fato mais de 80 dos candidatos selecionados não são físicos nem biólogos nem químicos.
Resposta: Alternativa A.
-
Galera acertei a questão mas não entendi porque tenho que somar os 8 candidatos F + B + Q se alguém puder me explicar agradeço.
-
GABARITO: LETRA A
Para esse tipo de questão há um MACETE excelente:
Toda questão com 3 conjuntos que pedir interseção basta:
* Somar os valores dos três conjuntos;
* Diminuir a interseção dos conjuntos;
* Somar com a interseção dos 3 conjuntos;
* O resultado deve ser subtraído pelo valor (universo).
Ou seja:
80+90+55-32-23-16+8=162
162-250=88
Prático e rápido como deve ser!
Difícil é editar esse texto no bloco de notas do QC.
Bons estudos!
-
Obrigada Prof Ivan pela explicação
-
GENTE QUESTÃO SIMPLES... so fazer o diagrama e pular para os itens, e ainda de quebra o item correto é o A..kkk
33 + 24 + 50 + 8 + 24 + 15 + 8 = 162. AI É SO VER QUANTO É O TOTAL E SUBTRAIR
250 - 162 =
88
** FAÇA SEMPRE O DIAGRAMA COM CALMA E TENTE ENTENDER A QUESTÃO POR TODOS OS ANGULOS ANTES DE COMERÇAR A FAZÊ-LO . :)
-
O importante é começar a encontrar os resultados seguintes subtraindo-os das interseções. Sendo que é melhor começar pelo valor agregado aos três elementos.
-
Pelo raciocínio que fiz, apenas em Física tem 43 candidatos. Nesse caso a "b", seria correta também? Alguém encontrou esse número (43 - F)?
-
Rafael Breviglieri,
É necessário somar a intersecção dos três ( 8), pois fazem parte do universo do conjunto de 250 candidatos (total)
Então seguindo o raciocínio da Andressa Castro, conseguimos concluir o exercício.
Sempre faço da seguinte forma:
Acho os valores somente de F, Q e B ( quando a questão só dá o total destes, você deve achar o que somente pertence a F,Q e B).
Achando os valores, e fazendo os cálculos das intersecção entre essas ( vide exemplo Andressa Castro) encontramos todos os valores do conjunto. Assim para achar o que não pertence a nenhum deles ( o que está fora dos conjuntos), eu somo o total de F ( 80- inclui os valores de 15+8(OLHA O 8 AQUI!! A INTERSECÇÃO DOS TRÊS!+24+33 ) + 24 ( que inclui somente o valor de Q, uma vez que já inclui as intersecções do F , não posso repetir) + 8 ( intersecções de Q e B) + 50( somente valor de B, uma vez que já inclui as intersecções do F que pega a de B), portanto fica : 80+24+50+8+z(valor de fora dos conjuntos)= 250, temos Z=88.
-
Podemos desenhar os conjuntos dos candidatos formados em física, em biologia, e em química. Veja que já representei aqueles oito candidatos que são formados nas três áreas ao mesmo tempo:
Sabemos que 32 são formados em biologia e física. Destes, sabemos que 8 também são formados em química, de modo que o total de pessoas formadas apenas em biologia e física ( e não formadas em química) é 32 - 8 = 24. De maneira análoga observe que o total de pessoas formadas apenas em química e física é igual a 23 - 8 = 15, e o número de pessoas formadas apenas em biologia e química é igual a 16 - 8 = 8. Colocando essas informações no diagrama ficamos com:
Temos 80 candidatos formados em física ao todo. Subtraindo aqueles que também são formados em alguma outra área ficamos com 80 - 24 - 8 - 15 = 33 candidatos formados apenas em física. De maneira análoga, temos um total de 90 candidatos formados em biologia, de modo que o total de candidatos formados apenas nessa área é igual a 90 - 24 - 8 - 8 = 50. Por fim, temos um total de 55 candidatos em química, de modo que o total de candidatos com apenas essa formação é 55 - 15 - 8 - 8 = 24. Colocando essas informações no diagrama:
Analisando as alternativas:
a) mais de 80 dos candidatos selecionados não são físicos nem biólogos nem químicos.
O número de candidatos que são físicos, biólogos ou químicos é dado pela soma das regiões no diagrama: 33+15+8+24+24+8+50 = 162. Portanto, os candidatos que não tem nenhuma dessas formações são 250 – 162 = 88. Item CORRETO.
b) mais de 40 dos candidatos selecionados são formados apenas em Física.
ERRADO, são 33.
c) menos de 20 dos candidatos selecionados são formados apenas em Física e em Biologia.
ERRADO, são 24.
d) mais de 30 dos candidatos selecionados são formados apenas em Química.
ERRADO, são 24.
e) escolhendo-se ao acaso um dos candidatos selecionados, a probabilidade de ele ter apenas as duas formações, Física e Química, é inferior a 0,05.
Temos 15 candidatos com essas duas formações apenas, em um total de 250. A probabilidade de selecionar um desses 15 é de 15/250 = 0,06 = 6%. ERRADO.
RESPOSTA: A