-
Questão A = 160 - 100 = 60 pessoas
Questão B = 250 - 60 = 190 pessoas
A e B = 100 pessoas
Nenhuma = 180 - 60 = 120 pessoas
60 + 190 + 100 + 120 = ; X =470 PESSOAS
-
Mateus tire uma dúvida.Quando vc tira as 100 pessoas que acertaram as 2 questões das 160 que acertaram a questão A não deveria fazer o mesmo com as 190 pessoas que acertaram a questão B????. Ou seja, as 100 pessoas são comuns,portanto acertaram as questões A e B, que nos levaria a um resultado de 370 pessoas.
-
Tiago Freitas observe note que quando a questão diz que exatamente 250 pessoas acertaram uma das duas questões temos o seguinte:
Questão A = 60, portanto para chegar a 250 faltam 190 pessoas, ou seja, 190 acertaram a questão B. Logo em seguida ele diz o seguinte: Que exatamente 180 pessoas erraram a segunda questão, porém eu posso e devo concluir que dentro dessas 180 pessoas estão aquelas que acertaram tão somente a questão A, então para saber quantas erraram as duas questões eu preciso retirar os 60 candidatos, com isso fica: 180 - 60 = 120 erraram as duas questões , para saber o total basta somar como fiz no primeiro comentário: 60(acertaram somente a A) + 190(acertaram somente a B) + 100(acertaram as duas questões) + 120(acertaram nenhuma questão) = 470 pessoas.
Talvez sua maior dúvida deveria estar por conta se era preciso diminuir 190 - 100, porém NÃO PODERÁ FAZER ISSO pois a questão já deixa claro que 250 pessoas acertaram uma e apenas uma questão, então como já sabemos que 60 acertaram a questão A conclui-se que 190 acertaram a B.
-
Obrigado mateus taliuli
-
1 - Começa-se pela interseção: 100 Pessoas no meio;
2 - Subtrai quem acertou a questão A 160- 100= 60 pessoas;
3 - Sei que quem acertou ou A ou B são 250, logo 250-60 = 190 Pessoas;
4 -Se 180 erram a B, temos um grupo que errou a B e acertou a A + quem errou as duas; 180-60 = 120;
5 - Soma tudo temos 470 pessoas;
-
Se 100 pessoas acertaram as duas questões, sobram 60 que acertaram apenas a primeira. Se 250 pessoas acertaram somente uma das questões, tirando as 60 que acertaram somente a primeira, sobram 190 pessoas que acertaram somente a segunda. Das 180 pessoas que erraram a segunda questão, sabe-se que 60 acertaram a primeira, ou seja, 120 pessoas (180-60) erraram as duas questões. Por fim: 60 (que acertaram a primeira) + 100 (acertaram ambas) + 190 (acertaram a segunda) + 120 (erraram as duas) = 470 pessoas responderam as questões.
-
Excelente explicação Mateus Taliuli ... Conseguiu esclarecer a minha dúvida também! Parabéns e obrigada por compartilhar conosco.
-
Resolvendo:
1° Questão = 160 - 100 = 60 pessoas
2° Questão = 250 - 60 = 190 pessoas
1° e 2° = 100 pessoas
Nenhuma = 180 - 60 = 120 pessoas
Logo:
X = 60 + 190 + 100 + 120 = 470 pessoas
Resposta: Alternativa D.
-
A resolução do professor QConcursos é péssimo! :(
-
Das 180 pessoas, uma parte delas acertou somente a primeira questão (60 pessoas), e uma parte errou as duas questões (120). Como no diagrama nós só representamos a quantidade de pessoas que acertaram alguma coisa ou ambas as coisas, deixaremos o 120 de fora do diagrama. Sendo que esse 120 entra na soma total de pessoas do grupo que responderam a avaliação. Quem tentou usar a fórmula e se embananou na hora de subtrair a intersecção, saiba que para usar a fórmula seria preciso acrescentar o 100 ao190, senão não acha o 470 na soma final...pela fórmula: 160+290-100+120=470
Gabarito D
-
Questão A = 160 (acertaram A) - 100 (acertaram A e B) = 60 pessoas acertaram somente A
Questão B = 250 (acertaram apenas uma) - 60 (acertaram somente A) = 190 pessoas acertaram somente B
Acertaram A e B = 100 pessoas
Erraram a B = 180 pessoas
Segui a seguinte linha de raciocínio:
Eu tenho um grupo com X pessoas, que responderam 2 questões e independente de quem acertou ou errou cada uma, a quantidade de pessoas que responderam as duas questões é a mesma tanto para "A" como para "B". Portanto se eu identificar todas as respostas certas e erradas de uma questão eu consigo saber quantas pessoas eu tenho neste grupo.
Olhando os dados acima, eu consigo fechar o grupo de pessoas que responderam a questão B, pois eu tenho todos os dados de erros e acertos desta questão.
190 (acertaram B) + 100 (acertaram B e A) + 180 (erraram B) = 470
Ou seja para a questão "B", do total de 470 pessoas, 290 acertou esta questão e 180 a errou.
Gabarito D) 470
Foi a forma que eu encontrei para resolver a questão :)
-
Para mim, o problema ficou nesses 120 que erraram as duas questões. Não vejo indício para concluir isso.
-
Pra quem é visual, assistam a explicação no link da Samira. É excelente.
-
Eu fiz o seguinte:
1° passo: peguei o número de pessoas que acertaram; erraram uma das questões e subtraí pelo número de pessoas que acertaram todas as questões:
160 (acertaram somente a primeira) - 100 = 60
250 (acertaram somente uma) - 100 = 150
180 (erraram somente a segunda) - 100 = 80
2° passo: somei todos esses resultados
60+150+80 = 290
3° passo: subtraí esse valor para cada número de pessoas
290-160 = 130
290-100 = 190
290-250 = 40
290-180 = 110
4° passo: a soma desses resultados é 470.
-
Acertou as 2 Q = 100
Acertou somente a Q1 = 60 (160 - 100)
Acertou apenas uma das Q --> 60 + X = 250 --> X = 190
Não acertou a Q2 = 120 (180 - 60, que acertou só a Q1)
Soma-se 60 + 100 + 190 + 120 = 470
-
Poxa este "exatamente" aí me ferrou
-
Assita a aula:
https://www.youtube.com/watch?v=KH0zJ99aKIQ&t=11s
-
Gabarito: D
-
Juro que não consigo entender o porquê dessa questão, não consigo entender a diferença entre 180 e 60.....
-
Comentário do professor: "Nenhuma = 180 - 60 = 120 pessoas "
???????????????????????
Também travei no 120 = 180 que erraram B - 60 que acertaram A = NENHUMA....
Confuso demais, só por Deus...
-
Camila, o exercício diz que 180 pessoas erradam a segunda questão. No entanto, no enunciado foi dito que 60 pessoas acertaram a primeira questão apenas. Logo, se eles acertaram a primeira questão APENAS, significa dizer que eles ERRARAM A SEGUNDA QUESTÃO.
Daí, retomando o início, quando foi dito que 180 erraram a segunda questão, termos que tirar 60, vimos que acertaram APENAS a primeira questão...
-
cara to moendo de estudar, dai quando acho que estou quase lá aparece uma questão dessa^^. PQP
-
O comentário do professor não explicou absolutamente nada. Parece que o cara comentou com pressa.
-
BOA TARDE GALERA !
TENTEM MONTAR O DIAGRAMA DE VENN E FICARÁ MAIS FÁCIL DE VISUALIZAR O PORQUE DA DIFERENÇA ENTRE 180 E 60. UMA TÍPICA QUESTÃO ENVOLVENDO PROPRIEDADES DE CONJUNTOS.
-
FINALMENTE ENTENDI....!!!!
Compartilhar ... pra ver se ajuda alguem....:
(chamar a questão 1 de A e questao 2 de B)
1º) 160 acertaram a questao A
2º) 100 acertaram as duas questoes ..... entao 160-100 = 60 ( Nao entendia o porque desse bendito 60;é porque a questao diz que 160 acertaram EXATAMENTE a A mas não APENAS a A - então esses 60 são as pessoas que acertaram APENAS a questão A)
3º) diz que 250 acertaram apenas UMA DAS DUAS QUESTOES - se sabemos já que exatamente 60 acertaram a A entao sobraram 190 que acertaram apenas a questao B)
4º) 180 no total erraram a questao B ... 180-60(esses 60 é aquele que já descobrimos que erraram porque acertaram APENAS questao A)= 120...
5º) 60(apenas A)+ 100(das duas)+ 190(apenas da B)+120(que erraram a B) = 470 pessoas.
-
mano toma muito tempo. força guerreiro,vamos conseguir
-
Vou jogar meu laptop na parade de ódio!
-
Explicação no youtube: https://www.youtube.com/watch?v=KH0zJ99aKIQ
-
Enunciado bosta.. padrão do lixo da VUNESP
-
nao tem nada de bosta no enunciado...
-
Típica questão pra lascar com a vida do concurseiro
-
Se o exercício fala que EXATAMENTE 160 acertaram a primeira, não faz o mínimo sentido subtrair 160 de 100 pqe NÃO FORAM 60 QUE ACERTARAM A 1ª, E SIM 160! Que coisa sem sentido!
-
Gabriela, nessa parte aí eu até que entendi, pois a questão disse ''exatamente 160 acertam a primeira questão'' e não ''160 acertaram apenas a primeira questão''. Como na interseção já tem 100, então tem que subtrair 160-100 que é igual a 60, daí dá exatamente 160. Agora, se dissesse que ''160 acertaram apenas a primeira questão, então não teríamos que subtrair, deveríamos somar o 160 com a interseção para saber o total de pessoas que acertaram a questão 1. Mas a dúvida maior, que eu empaquei mesmo, foi na parte dos ''180 erraram a segunda questão''. Daí o nome da matéria, puro raciocínio lógico mesmo. Cara, que coisa, agora entendi que esses 180 que erraram a questão 2, devemos subtrair 60 porque, se 60 acertaram a 1 então erraram a 2 né!!! Daí fica 120+60+100+190=470.
Comentários excelentes, ajudaram a esclarecer bem!!!! Enchi a folha de diagramas, mas não erro mais!
-
acertaram ambas : 100
acertaram somente a primeira : 60( 100 já computados na "ambas")
acertaram somente segunda: 190 ( 250 -60)
acertaram nenhuma : 120 ( 180 erraram a segunda. Como já visto, erraram a segunda e acertaram somente priemira = 60, então sobrou 120, que erraram ambas.)
-
Só há 4 possibilidades, acertar só A ou acertar só B ou acertar A e B ou errar A e B.
Então o total de pessoas será as que acertaram só A + as que acertaram só B + as que acertaram A e B + as que erraram A e B
1) 160 acertaram A. Dentro desses 160 estão as pessoas que acertaram só A e as que acertaram A e B. Dessas, as que acertaram A e B foram 100, então as que acertaram só A foram 60 (160 - 100).
2) 250 acertaram apenas uma das questões. Já sabemos que 60 acertaram só A, então as que acertaram só B foram 190 (250 - 60)
3) 180 erraram B. Dentro desses 180 estão as pessoas que erraram só B e as que erraram A e B. Dessas, 60 erraram só B (que é a mesmo que dizer que acertaram só A), então as que erraram A e B foram 120 (180 - 60)
Voltando à nossa fórmula para calcular o total:
total de pessoas = as que acertaram só A + as que acertaram só B + as que acertaram A e B + as que erraram A e B
total de pessoas = 60 + 190 + 100 + 120 = 470
-
180 pessoas ERRARAM a 2ª questão... 180 não acertaram a 2a questão, isso quer dizer que: do total de pessoas avaliadas, 180 não pertencem ao conjunto das que acertaram a 2a questão. Como nesse grupo (que não acertaram a 2a) já haviam 60 (as que acertaram somente a 1a questão), essa diferença: 180 - 60 dá a quantidade de pessoas avaliadas que não acertaram questão alguma. = 120
-
NÃO ENTENDI A LOGICA DA CONTA QUE CHEGA EM 120. HELP ME.
-
É so fazera soma de 160+100+250= 510.
Depois é so fazer a conta de menos 510-180= 470
-
AVALIAÇÃO A/B
160 acertaram A
100 acertaram A e B
250 acertaram A ou B (somente)
180 erraram B
x Erraram A
Dos que acertaram A apenas 60 acertaram só A, os outros 100 acertaram A e B
Se 250 acertaram ou A ou B, então 250 - 60= 190 acertaram só B
dos 180 que erraram B, 60 acertaram A, mas o restante, 120, errou as duas questões A e B
Total de pessoas que realizaram a prova foi:
100 (acertaram as duas) + 60 (acertaram A) + 190 (acertaram B) + 120 (erraram as duas)
100+60+190+120
R: 470
-
Denis Araújo estou adorando os seus comentários até aqueles com excesso de raiva ...
Espero que passe no TJSP....
-
QUESTÃO PODRE
-
O 120 vem daqui:
Se 250 acertaram apenas uma das duas questões, então:
100 = ambas as questões
60 = somente a primeira, pois o enunciado diz que os acertos da primeira foram 160.
190 = somente a segunda, pois 250(que acertaram apenas uma)-60 das que acertaram somente a primeira.
120 = se 180 erraram a segunda, devemos subtrair 60, pois foram os que erraram a segunda e acertaram a primeira. Os 120 que sobram são os que erraram ambas.
Some tudo :100+120+190+60 => 470
-
Possibilidades:
Acerto Acerto = 100
Acerto Erro = 160 - 100 = 60 (acertaram somente a 1ª 60 e esses mesmos erram a 2ª)
Erro Acerto = 250 - 60 = 190 (apenas uma questão 60 + 190 = 250)
Erro Erro = 180 - 60 = 120 (180 erraram a 2ª, como 60 acertam somente a 1ª, erraram as duas 120)
Total = 100+60+190+120 = 470
-
AJUDA MUITO ENTENDER OS 120! https://www.youtube.com/watch?v=KH0zJ99aKIQ (3:00)
-
1ª QUESTÃO --------------- 2ª QUESTÃO------------- TOTAL
ACERTO ACERTO ACERTO -- 100------------------ 100
ACERTO ERRADO 160 -60-------------- 60
ERRADO ACERTO 250-60---------------190
ERRADO ERRADO 180-60-------------- 120
100+60+190+120= 470
ALTERNATIVA D
-
Quando o enunciado diz 180 erraram a segunda, não podemos assumir que é só a segunda! Alguns desses podem ter errado a segunda mas também a primeira, por isso não concordo com retirar 60 (180 - 60) para encontrar os que erraram a primeira. O enunciado por mais que dissesse "EXATAMENTE" 180 erraram a segunda, não disse que eles erraram "SOMENTE" a segunda.
Quando resolvemos exercicios semelhantes que dizem: o total de pessoas que acertou A e o total de pessoas que acertou SOMENTE A, fica claro, mas neste caso o exercício tentou extrapolar.
-
Essa questão facilita muito fazer por diagrama de venn galera.
Monte dois circulos, como questão 1º e questão 2º, contendo uma intersecção depois só preenchendo, na intersecção vai os 100 candidatos que acertaram as duas questões. Depois é ir montando conforme o autor pedi no enunciado.
Depois de feito é só somar os valores que será 470, ou seja, 60 pessoas acertaram somente a questão de número 1º, 190 pessoas acertaram somente a questão de número 2, 100 pessoas acertaram as duas questões e por fim 120 pessoas erraram as duas questões.
Somando 60 + 190 + 100 + 120 = 470
Alternativa D
-
Essas questões de conjunto exigem muito de interpretação. Quem está com dificuldade é bom dar uma treinanda na leitura.
-
Gabarito D
-
Amanhã eu volto :(
-
o que eu não entendi foi pq não considerar a intersecção pra fechar o conjunto da segunda questão e como que 180 erros é de 120 pessoas??????????????????????????
-
250 PESSOAS ACERTARAM APENAS UMA DAS DUAS QUESTÕES. NÃO SEI QUAL DELAS, MAS POSSO INFERIR QUE FAZ PARTE DE UM TODO.
QUESTÃO 1 = A
QUESTÃO 2 = B
O QUE É 100? = É intersecção, 100 PESSOAS ACERTARAM AS DUAS QUESTÕES
O QUE É A? A = 160 - 100, (160 PESSOAS ACERTARAM A PRIMEIRA QUESTÃO)
O QUE É B? B = -180 - 100, (-180 ERRARAM A SEGUNDA QUESTÃO)
DESTA FORMA,
A+B (sem a intersecção)
60-280 = -220,
UTILIZANDO OS ELEMENTOS E SUBTRAINDO-OS DO CONJUNTO DE (A+B), 220 É O QUE PASSOU.
(250 + 160 + 180 + 100) - 220 = 690 - 220 = 470
-
Vou compartilhar como eu resolvi está questão.
Primeiramente desenhe um retângulo GRANDE e dentro dele dois círculos fazendo uma interseção entre eles.
O 1º será representado por quem acertou a Qstão1 e o 2º será representado por quem acertou a Qstão2, a INTERSEÇÃO quem acertou as duas questões e fora dos círculos quem ERROU as DUAS.
BELEZA, até aqui já temos o desenho do nosso DIAGRAMA, ok?
> 160 pessoas desse grupo acertaram a primeira questão. Vamos escrever dentro do 1º círculo 160.
> 100 pessoas acertaram as duas questões. OPA!!!!! Se 100 acertou as duas questões, devemos apagar os 160 do 1º círculo e marcar somente 60, pois passaremos a ter 100 na INTERSEÇÃO, resultando em 160 Qstões acertas na 1ª Questão.
TEMOS ATÉ AQUI >>> SOMENTE 1ªQ = 60 INTERSEÇÃO DA 1ª/2ªQ = 100 2ªQ NÃO TEMOS AINDA
> 250 pessoas acertaram apenas uma das duas questões. Esqueça da INTERSEÇÃO !!! SE 250 acertaram APENAS 1 das DUAS QUESTÕES e já temos 60 que acertaram a 1ª Qstão então 190 pessoas acertaram SOMENTE a 2ª Qstão.
FICANDO >>> SOMENTE 1ªQ = 60 INTERSEÇÃO DA 1ª/2ªQ = 100 SOMENTE 2ªQ = 190
Momento de muita CALMA agora... 180 pessoas erraram a segunda questão.
As 60 pessoas que acertaram a 1ª estão entre estas 180, pois quem acertou a 1ª errou a 2ª. Mas e o restante? 120 no caso...
Podemos concluir que 120 ERRAM as DUAS QUESTÕES
180 - 60 = 120 Pessoas estão fora dos círculos.
Concluindo...
SOMENTE 60 1ª QUESTÃO INTERSEÇÃO DA 1ª/2ªQ = 100 SOMENTE 190 2ªQUESTÃO ERRAM AS DUAS = 120
Este grupo é composto por 470 PESSOAS.
Espero ter ajudado...
-
Obrigado Alexandre Cristiano! Você ajudou muito!
-
Tenho que ter cuidado com a interpretação deste tipo de questão:
Estava me perdendo na informação que 160 acertaram a primeira questão.No meu entendimento era que 160 acertaram "APENAS" a primeira questão.
Eu mesmo, meio que subconsciente coloquei esse "APENAS" que me atrapalhou na resolução.
-
Podemos criar o conjunto das pessoas que acertaram a primeira questão e o conjunto das pessoas que acertaram a segunda. Temos:
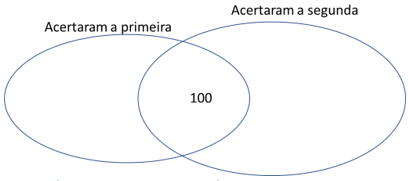
Veja que já coloquei as 100 pessoas que acertaram as 2 questões. Como 160 acertaram a primeira, vemos que as que acertaram SOMENTE a primeira questão são 160 – 100 = 60 pessoas. Como 250 pessoas acertaram apenas 1 questão, e já sabemos que 60 acertaram só a primeira, as que acertaram somente a segunda são 250 – 60 = 190 pessoas. Ficamos com:

A última informação é: exatamente 180 pessoas erraram a segunda questão. Neste grupo estão aquelas 60 pessoas que só acertaram a primeira questão. Além disso, temos mais 180 – 60 = 120 pessoas que erraram as DUAS questões, e precisam ser representadas também. Ficamos com:
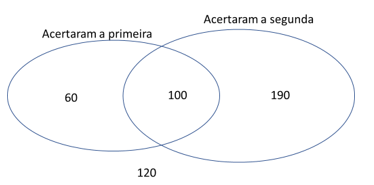
O total de pessoas é 60 + 100 + 190 + 120 = 470.
Resposta: D
-
melhor resolucao que eu ja vi! so assim consegui entender kkkkk excelente explicacao
-
Valeu Alexandre Christiano, ótima explicação!!!
-
Primeiro separei as informações:
Acertaram a 1° Questão: 160 pessoas.
Acertaram a 2° Questão: 100 pessoas.
Calculo para saber a diferença: 160 - 100= 60 pessoas.
Acertaram APENAS 1 das duas questões= 250 pessoas
Erraram a 2° Questão: 180
Calculo para saber a diferença: 250 - 180= 70 pessoas.
Agora só somar:
160 + 70 = 230
180 + 60 = 240
230 + 240= 470
resposta correta: D 470.
-
Gabarito:D
Principais Dicas:
- Principais questões são de 2 ou 3 conjuntos.
- Primeiro acha sempre a intersecção e sai complementando. Ex: A ∩ B = 10; A= 20; B=30. Logo, A tem apenas 10 e B tem apenas 20.
- Caso não tenha a intersecção? Soma tudo e subtrai do total. Ex: A= 20; B=30; Total= 40. Logo, a intersecção é 50-40=10.
- E cuidado nas questões que ele fala APENAS, SOMENTE etc.
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
-
https://www.youtube.com/watch?v=SouW9yGoqvA
-
Quando o capiroto não tem nada para fazer, inventa uma questão dessa.
-
Eu já tentei de todos os jeitos raciocinar nessa questão e chegar ao gabarito sozinha, até vi o vídeo com a explicação, mais é incrível, sabe quando uma coisa não entra na sua cabeça? E pior que eu gosto de qstões de conjunto, mais essa aí... deve ser pq estou cansada.
-
Discordo das explicações.... quando a questão afirma "Sabendo-se que exatamente 160 pessoas desse grupo acertaram a primeira questão", não necessariamente as 160 acertaram APENAS a primeira questão... dentro dessas 160 podem ter pessoas que acertaram só a primeira e pessoas que acertaram a primeira E a segunda....
-
Gabarito: D
Para ver o diagrama bastar copiar e colar, na barra de endereços do navegador, o link: https://sketchtoy.com/70176638
Interseção: 100 "100 pessoas acertaram as duas questões"
1º: 100 + 60, pois "160 pessoas desse grupo acertaram a primeira questão"
2º: 190, pois "exatamente 250 pessoas acertaram apenas uma das duas questões". Para chegar ao valor 190 devemos fazer o cálculo (250-60 = 190)
Por fim, "180 pessoas erraram a segunda questão". Com isso, colocamos o valor 120 fora dos dois conjuntos já que temos os 60 que acertaram apenas a 1º o que significa que erraram a 2º.
-
Questão dificílima! Recomendo deixar por último ou chutá-la, em última instância.
-
Comecei a fazer essa questão no dia 30 setembro e finalizei só agora.
-
Desisto...diagrama de venn que envolva contas, vou nem tentar, será chute na certa!
-
O nó da questão é: 180 pessoas erraram a segunda questão (outro detalhe importantíssimo - não posso afirmar que esse 180 acertaram a primeira questão.
desses 180 se 60 acertaram apenas Questão 1). Entao 180 - 60 = 120 que pode ter errado ambas questoes
60 - acertou apenas Questao 1
100 - acertou Questao 1 e 2
190 - acertou apenas Questao 2 (250 - 60 que acertaram apenas Questao 1)
120 - nao acertou nenhuma das questoes esta fora, porém no grupo X de pessoas
Total: 470