-
Como 6 torneiras têm 1/3 a menos da vazão, podemos considerar que as seis torneiras possuem 2/3 da vazão "normal". Somando tais vazões (2/3 + 2/3 + 2/3 + 2/3+ 2/3+ 2/3), teremos o equivalente à vazão de 4 torneiras "normais". Portanto, na verdade, as seis torneiras equivalem a quatro! Lembrando que uma delas apresenta a mesma vazão anterior, então temos 5 torneiras na segunda ocasião. Com essa informação, podemos aplicar regra de três composta:
4,5 H - 7 torneiras - 8 tanques
X - 5 torneiras - 6 tanques
4,5/x = 5/7 x 8/6
20x = 94,5
x = 4,725H
0,725 x 60 = 43,5 minutos
0,5 x 60 = 30 segundos
-
Atribuindo 9 para a vazão de cada torneira, primeira ocasião: 7 torneiras = 63(7x 9(vazão)); Na segunda ocasião temos vazão de 2/3 x 9 = 6 ; seis torneiras com vazão 6 ( 6x6=36) e uma torneira com vazão 9, total de 36+9=45 . E considerando o tempo em minutos ( 4h30min = 270min ).
Regra de Três Composta:
Vazão Tanque Tempo(minutos) 1: 63 8 270 2: 45 6 x
270/x = 8/6 .45/63
X= 283minutos = 4h43min30s
-
Questão relativamente tranquila para a maioria dos concurseiros, mas eu sempre me confundo no cálculo das questões envolvendo torneiras.
Portanto, cheguei às seguintes conclusões na resolução desse tipo de questão:
1.ª) O sinal de igual (=) fica do lado da incógnita (x);
2.ª) Quando for analisar se a relação é direta ou inversamente proporcional, tenha como referência o lado da incógnita;
3.ª) A operação do outro lado da incógnita é de multiplicação, e não de adição.
Por gentileza, me corrijam se eu estiver errado, pois tenho grandes dificuldades em matemática.
Acreditem! eu sempre me enrolo nesses três pontos.
-
Cainho Viegas,
Tb me confundo pra saber se é inversamente ou diretamente proporcional. No caso dessa questão, parece que quanto mais tempo menos torneiras precisam ser usadas e mais tanques serão enchidos. Assim, há inversão da fração correspondente às torneiras. Alguém pode confirmar se é isso mesmo?
-
Supomos que a torneira (A) obtenha a maior vazão e a torneira (B) tenha a menor vazão. Sendo assim, A possui uma vazão de 100%, enquanto que a torneira B possui 1/3 a menos do que a torneira A, matematicamente temos:
A = 100% = 1
B = A - 1/3(100%) = A - 1/3(1) = A - 1/3
Agora, basta aplicar uma regra de três composta ao problema, como abaixo:
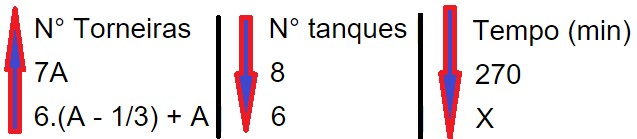
Assim:
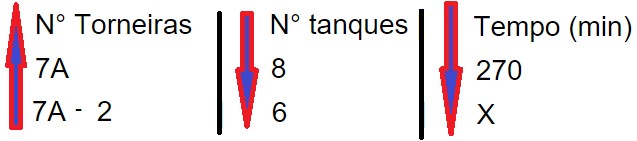
Resolvendo:
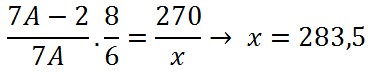
Sabemos que 4 horas e 30 minutos = 270 minutos, assim:
283,5 - 270 = 13,5 minutos, ou 13 minutos e 30 segundos, somando:
4 horas 30 min 00 seg
+ 0 horas 13 min 30 seg
-----------------------------------
4 horas 43 min 30 seg
Resposta: Alternativa D.
-
Para quem, assim como eu, se atrapalha com regra de três composta:
http://www.somatematica.com.br/fundam/regra3c.php
-
Prezado Elionaldo, por que vc atribuiu o número 9 para a vazão?
Grato
-
Sobre a relação entre as grandezas:
Incógnita está no tempo
Tanque x tempo = quanto menos tanques, menos tempo para enchê-los. Diretamente proporcional.
Torneiras x tempo = quanto mais torneiras estiverem funcionando, menos tempo para encher os tanques. Inversamente Proporcional
-
Ricardo Silva!
A questão fala que todas as torneiras têm a mesma vazão.
Adotei o 9 pra facilitar a operação de divisão com a fração 1/3.
Mas poderia ser ( 1, 2, 3, 4 , ...), como vou dividir por 1/3 aconselho usar um número que seja divisível por ele, no caso pra facilitar a divisão ( 3,6,9,12,15,...).
Mas poderia ser qualquer valor, desde que diferente de zero.
-
Considerando que 6 torneiras apresentam vazão 1/3 a menos eu multipliquei 6 * 2/3 = 4, ou seja estas 6 torneiras equivalem a 4 com vazão "normal".
Dessa forma, a regra de 3 ficou assim:
Torneiras Tanques Tempo (min)
7 8 270
5 6 X
Aprendi com o ótimo professor Josemar Alves dos Santos que:
"A que tem X você não mexe, as outras que se virem."
E observando a relação entre as grandezas, conforme o comentário da colega Laís FSS temos:
270/X = 5/7 * 8/6
270/X = 40/42
40X = 42 * 270
40X = 11340
X= 283,5
Depois é só transformar este valor em horas. O professor Vinícius Werneck apresenta o seguinte raciocínio:
Sabemos que 4 horas e 30 minutos = 270 minutos, assim:
283,5 - 270 = 13,5 minutos, ou 13 minutos e 30 segundos, somando:
4 horas 30 min 00 seg
+ 0 horas 13 min 30 seg
-----------------------------------
4 horas 43 min 30 seg
-
Putsssss!!!
Valeu Laís FSS, bem lembrado: A relação inversa ou direta entre as grandezas deve ser analisada em relação àquela que possui a íncognita, logo:
AUMENTANDO-SE o número de HORAS, AUMENTA-SE o número deTANQUES, para o MESMO NÚMERO deTORNEIRAS.
AUMENTANDO-SE o número de HORAS, DIMINUI-SE o número de TORNEIRAS, para o MESMO NÚMERO de TANQUES.
-
Alguém pode explicar nessa parte do cálculo do Devanir santos "6 * 2/3" porque foi mutiplicado por 2/3? não entendi.
Obrigado!
-
Definitivamente, leio e releio os comentários e não aprendo essa questão das torneiras. :(
-
Uma empresa precisa encher de água 14 tanques de igual volume. A empresa executará esse trabalho em duas ocasiões. Na primeira ocasião 7 torneiras, com a mesma vazão de água, enchem 8 desses tanques em 4 horas e 30 minutos. Na segunda ocasião, 6 dessas 7 torneiras apresentam vazão 1/3 a menos do que na primeira ocasião e uma delas a mesma vazão anterior.
O tempo gasto para que essas 7 torneiras encham os últimos 6 tanques é igual a...
1) Na 1ª situação temos:
torneiras = 7
hora = 4h e 30 minutos = 270 minutos (4x60 +30=270)
tanque= 8
2) Na 2ª situação temos:
torneiras:
6 dessas 7 torneiras apresentam vazão 1/3 a menos do que na primeira ocasião
LOGO: 1 torneira tem vazão de 3/3 = 1
6 apresentam vazão 1/3 a menos, ou seja, 3/3 - 1/3 = 2/3
Assim: 6(2/3) = 12/3 = 4
e uma delas a mesma vazão anterior. Ou seja, uma torneira tem vazão na razão 3/3 = 1
TOTAL das torneiras na 2ª situação: 4+1 = 5
hora: x
tanque: 6
ASSIM, TEMOS TODOS OS VALORES DA PROPORÇÃO COMPOSTA. COMO PROCEDER?
1) Pergunta para o sujeito o que ele está fazendo: Ei cara, o que você tá fazendo? Enchendo TANQUE. Logo, O TANQUE é a consequência e, por isso, deve ser isolado....
TORNEIRA HORA ------------------- TANQUE
7 270 MINUTOS 8
5 X 6
Na proposição composta você deve pegar os valores da esquerda que estão em cima e ao passar para a direita (consequência- tanque) descer: 7x270x6 = 11340
E vice versa: pegar os valores da esquerda que estão embaixo e, ao passar para a direita (consequência -tanque) subir: 5. X . 8 = 40x
40x= 11340
x= 283,5 (lembrando que o número após a vírgula pode ser multiplicado por 6, assim: 5x6= 30 segundos)
283/60= 4h e 43minutos
GABARITO LETRA D.
-
Considerando na segunda etapa que 6 torneiras apresentam vazão 1/3 "A MENOS", na realidade elas não apresentam um 1/3 das primeiras, mas 1-1/3 (a menos) = ou seja possuem vazão de 2/3 das primeiras, agora é só multiplicar por 6 * 2/3 = 4, equivalem a 4 com vazão "normal" e mais 01, total 05 torneiras iguais as primeiras.
Dessa forma, a regra de 3 ficou assim:
Torneiras Tanques Tempo (min)
7 8 270
5 6 ........ X
Pelo Bizu de multiplicar por linha com inversão do fator de produção, que nesse caso são os tanques. (observe, esse bizu só serve com até 03 grandezas, mas ajuda pra não perder tempo perguntando quais são as grandezas diretas e inversamente proporcionais)
7 x 6 x 270 = 5 x 8 x X
11340 = 40.X
X = 1340/40
X = 283,5 minutos = 283,5/60 = 4 horas mais uma fração de 0,725 = 60 x 0,725 = 43 minutos, mais fração de 0,5 = 60 x 0,5 = 30 segundos, total 4 horas, 43 minutos e 30 segundos.
-
Engraçado é ver a mudança de posicionamento do CESPE em questões semelhantes
Q31555
A coação física irresistível afasta a tipicidade, excluindo o crime. CERTO
Ué, o que se excluiria não seria a conduta?
-
A conduta está contida no fato típico, se não tem conduta, não haverá crime.
Fato Típico : CONDUTA, NEXO CAUSAL, TIPICIDADE e RESULTADO.
Na verdade, a questão que você trouxe, coaduna com o entendimento adotado pela banca.
Bons papiros.