-
Galera acho que só colocar a letra não ajuda em nada, pois isso o site já faz né.
-
Alguém pode explicar como resolver ste item?
-
Sabemos que um argumento é válido se, e somente se, todas às vezes que suas premissas
são verdadeiras, sua conclusão também o é. Assim, resolvendo pelo método direto, onde:
(1) em todos os casos (linhas da tabela-verdade) em que as premissas são verdadeiras a
conclusão é verdadeira e, portanto, o argumento é válido; ou
(2) há um caso (linha da tabela-verdade) com premissas verdadeiras e conclusão falsa e,
portanto, o argumento não é válido.
Então:
Argumento I:
Premissa 1: Ou a água é gelada ou José fica com sede. = A v B
Premissa 2: Não chove e José fica com sede. = ~C ^ B
Conclusão: A água não é gelada e não chove. = ~A ^ ~C
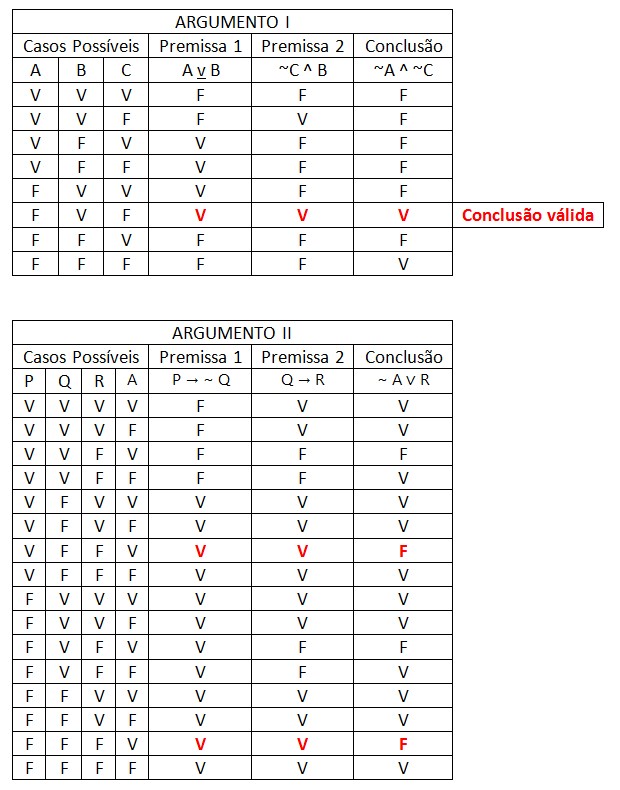
Aqui, existem dois casos em que as premissas são verdadeiras e conclusão é falsa e, portanto o argumento não é válido. Argumentos dessa forma são chamados de falácia da negação do antecedente.
Resposta: Alternativa C.
-
Explicando do meu jeito:
Gosto de partir do 'E'
PREMISSAS:
1 - Nao chove ^ José fica com sede = V
1 - Já sei que esse dois são verdadeiros!
2 - OU a água é gelada OU José fica com sede = V
2 - OU .. OU: Um dos dois é falso. Logo, como já sei que Jóse fica com sede (V), sei que o outro lado é falso (A ÁGUA *NÃO* É GELADA).
portanto, a partir das premissas, posso concluir que A ÁGUA *NÃO* É GELADA *E* NÃO CHOVE.
-
Parte dois, achei que era válido... acho que a resposta é que não posso deduzir [ ~A ~], já que não aparece nas premissas e estou com "OU". Logo argumento inválido.
-
Pessoal, só há um caminho:
Construir a tabela verdade para os dois Argumentos (infelizmente não farei isto aqui, por ser muito trabalhoso) e se, ao observar o cruzamento das tabelas em cada argumento você perceber que
(1) em todos os casos (linhas da tabela-verdade) em que as premissas são verdadeiras a
conclusão é verdadeira, o argumento será válido; ou
(2) há um caso (linha da tabela-verdade) com premissas verdadeiras e conclusão falsa,o argumento não será válido.
Logo, apenas saliento que este problema não deve ser feito com lógica vulgar ou elocubrações que casam com esta ou aquela resposta, mas com a tabela verdade.
O gaba é C
-
Olhem os comentários do professor.
-
Argumento I
Premissa 1: Ou a água é gelada ou José fica com sede. AG V JFS
F V (V)
Premissa 2: Não chove e José fica com sede. ~CH ∧ JFS
V V (V)
Conclusão: A água não é gelada e não chove. ~AG ∧ ~CH
V V (V)
PREMISSAS VERDADEIRAS E CONCLUSÃO VERDADEIRA = ARGUMENTO VÁLIDO
===========================================================================
Argumento II
Premissa 1: P → ~ Q
V/F F (V)
Premissa 2: Q → R
F F (V)
Conclusão: ~ A ∨ R
V F (F)
PREMISSAS VERDADEIRAS E CONCLUSÃO FALSA = ARGUMENTO INVÁLIDO
_____________________
GABARITO LETRA C
_____________________
-
Letra C.
c) Certo.
Argumento I - Válido!
Premissa 1:
Ou a água é gelada ou José fica com sede. (V)
(F) (V)
Premissa 2: Não chove e José fica com sede. (V)
(V) (V)
Conclusão: A água não é gelada e não chove. (V)
Argumento II - Inválido!
Premissa 1: ( P ) → ~Q : V
? (V) : V
Premissa 2: Q → R : V
(F) (F) : V
Conclusão: ~A v R (F)
(F) "ou (F) : F
Questão comentada pelo Prof. Márcio Flávio
-
essa foi de lascar