-
errado,
pelo que entendi e facil, 40 grego + 60 que estudam espanho sao 100, sobram 80, entao nao tem ocmo 90 estudarem ingles.
-
fazer diagrama de ven, com as interseçoes de ingles e espanhol, e grego separado. 40 estudam somente grego. na interseção do ingles e espanhol coloca-se 40, somente no espanhol 20, pois 60 estudam espanhol e sobram 80 que so estudam ingles.
-
Não é possível concluir algo já que não há informações completas:
Eu sei que há:
- 60 alunos estudando espanhol (mas que também podem estudar outros idiomas);
- 40 alunos estudando somente inglês e espanhol;
- 40 alunos somente estudando grego.
Mas eu NÃO sei:
- quantos alunos estudam só inglês, ou inglês e grego, ou inglês grego e espanhol.
Não é possível concluir a afirmação da questão apenas com os dados fornecidos - essa é a razão de estar ERRADA essa questão.
-
Discordo da Colega acima, pois com base nas informações passadas é possível sim montar o diagrama de ven e responder a questão corretamente, ou seja, 80 alunos estudam somente ingles;
-
De acordo com o diagrama de Venn abaixo, podemos perceber que já temos o total de 100 alunos já estudando os idiomas especificados no diagrama, logo restam 80 alunos a serem alocados em outras turmas, o que seria impossível que mais de 90 alunos estudem somente inglês.
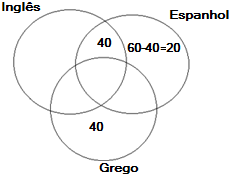
A resposta é: Errado.
-
180 - 60 - 40 = 80
-
180 ALUNOS
40 estudam somente grego, então: 180- 40 = 140
20 estudam somente espanhol (60 - 40 que estudam Inglês e Espanhol= 20), então: 140-20= 120
120 - 40(alunos que estudam inglês e espanhol) = 80 alunos que estudam somente INGLÊS
Resposta: ERRADA
-
a questão fala em 60 alunos que estudam espanhol e não APENAS espanhol ... tem gente raciocinando errado e acertando a questão.
-
Nao há como afirmar quantos alunos estudam somente inglês, Mas o valor máximo permitido seriam 80 Alunos
-
40 estudam somente inglês e espanhol, 40 estudam somente grego e 20 estudam espanhol somente.
40+40+20 = 100
180-100 = 80 (máximo que poderia ter só para inglês)
-
Não, não
Não é possível achar todas as informações não.
A única coisa que se pode concluir é que sobrou 80 alunos(ver comentário do thiago)!! Portanto, impossível 90 alunos estudarem somente Inglês.
Os 80 alunos que sobrou, devem ser distribuídos entre:
- Interseção entre os 3 grupos;
- Interseção daqueles que estudam inglês e grego;
-Aqueles que estudam somente inglês.
Sendo impossível, com os dados apresentados, descobrir a quantidade exata de alunos a serem alocados nos grupos que mencionei.
qualquer coisa manda um inbox, pois tenho limite de acompanhamento de comentários
Bons estudos meus amigos.
-
Tem-se de considerar a possibilidade maxima de alunos que somente estudam ingles, assim temos ->
X = Maximo que so podem estudar somente inglês.
N( X U Y U Z ) = N(Y) + N(X) + N(Z) - N(X Inter Y)
180 = 60 + (40+X) + 40 - 40
180 = 100 + X
X = 180 - 100
X = 80
80 < 90
-
40 só grego
90 só inglês
60 espanhol (sendo que aqui não é só espanhol, no entanto não podem estar os 90 que estudam só inglês nem os 40 só grego, pois estes sessenta estudam espanhol)
Somando 40+90+60 teríamos 190 alunos. Ou seja, está incorreta a questão, pois sabemos que temos um total de 180 alunos. Então não é possível que 90 alunos estudem só inglês, a possibilidade máxima de alunos que podem estudar só inglês é de 80.
Grego + espanhol : 40 + 60 = 100. Só sobram 80 para gostar só de inglês.
Gabarito: errado.
-
"20 estudam somente espanhol (60 - 40 que estudam Inglês e Espanhol= 20), então: 140-20= 120"
Discordo desse raciocínio porque a questão fala que 40 estudam inglês e espanhol, mas não diz a distribuição disso -- ou seja, pode ser 1 estudando ingles e 39 estudando espanhol.
-
Com as informações do problema já é possível perceber que o valor de alunos de 100. Como são apenas 180 alunos, é impossível colocar 90 em algum lugar. Questão errada.
-
Com as informações do problema já é possível perceber que o valor de alunos de 100. Como são apenas 180 alunos, é impossível colocar 90 em algum lugar. Questão errada. (Segui essa lógica básica também).
-
gente, cuidado!
não tem como 20 ser quem estuda SÓ espanhol, veja:
60 corresponde ao valor total de alunos que estudam espanhol, isso inclui interseção entre
-Espanhol + Inglês+ Grego ( E+I+G)- não sabemos
-Espanhol + Grego (E+G)- não sabemos
-Espanhol+Inglês (E+I) - 40
Logo, 60- 40 = 20, de forma que esse valor é o de (estudantes de espanhol) - (os estudantes de inglês + espanhol), note que para quantificar os alunos que estudam SÓ espanhol também precisaríamos subtrair desses 20 restantes (E+I+G) e ( I+G).
-
A questão traz um total de 180 alunos, sendo que:
40 estudam apenas grego...
40 estudam inglês e espanhol...
20 estudam apenas espanhol.
Deste modo, 180 - 100 = 80... então não tem como haver um número de alunos superior a este no inglês, logo, o gabarito é Errado.