-
QUESTÃO CERTA!
Considere X = gostam da I; Y = gostam da II; Z = gostam da I e da II; N = gostam de nenhuma (atividade)
X + Y + Z + N = 35
X + Y = 29
Y + Z = 28
Substituindo na expressão primeva:
Z + N = 6
X + N = 7
Agora tentando achar Y em função de N:
29 – Y + Y + 28 – Y + N = 35
-Y + N = -22
Y – N = 22
Y = 22 + N
A quantidade mínima será 22, destarte maior que 20.
Se algo estiver errado é só me mandar uma mensagem.
-
QUESTÃO CERTA!
Considere X = gostam da I; Y = gostam da II; Z = gostam da I e da II; N = gostam de nenhuma (atividade)
X + Y + Z + N = 35
X + Y = 29
Y + Z = 28
Substituindo na expressão primeva:
Z + N = 6
X + N = 7
Z = 6 - N
X = 7 - N
Sim, deve ser inferior a 7 (máximo 6), caso contrário Z seria um número negativo.Supondo que N fosse 6:
Z = 0; X = 1; Y = 28 → POSSÍVEL!
Se algo estiver errado é só me mandar uma mensagem.
-
QUESTÃO CERTA!
Considere X = gostam da I; Y = gostam da II; Z = gostam da I e da II; N = gostam de nenhuma (atividade)
X + Y + Z + N = 35
X + Y = 29
Y + Z = 28
Substituindo na expressão primeva:
Z + N = 6
X + N = 7
Agora tentando achar Y em função de N:
29 – Y + Y + 28 – Y + N = 35
-Y + N = -22
Y – N = 22
Y = 22 + N
Só substituir N por 4:
N = 4; Y = 26; Z = 2; X = 3 → POSSÍVEL!
Se algo estiver errado é só me mandar uma mensagem.
-
Certo
Essa questão dá para resolver sem conta, observamos que 29 técnicos gostam da atividade 1 com um total de 35 técnicos podemos afirmar que o número de técnicos que não gostam, de nenhuma atividade nunca será maior que 6 pessoas partindo do princípio que 29 gostam da atividade 1.
-
Certo
Na verdade serão 26 técnicos que gostam das duas atividades.
-
Aos não assinantes:
R: C
São 22.
-
Q p*$*#$% de gabarito é esse?? 29-x+28=35 => x=22 Superior a 20 não, superior a 21 pois se fosse superior a 20, 21 satisfazeria a questão. Alguém pode explicar melhor??
-
Para termos a quantidade mínima de técnicos desse grupo que gostam das duas atividades, deveremos ter 0 pessoas deste grupo que não gostam de nenhuma atividade, logo:
29-x+28=35-0
x=22
Ou seja, a quantidade mínima de técnicos desse grupo que gostam das duas atividades é superior a 21 e não a 20, pois se fosse superior a 20, a condição de 21 técnicos deveria satisfazer a questão, o que não é o caso.
pois:
29-21+28 = 35-0
36=35 (errado pois teríamos 36 técnicos dum total de 35)
Suponhamos agora que fosse 25 técnicos que gostasse das duas atividades, teríamos:
29-25+28=35
32=35 (há essa possibilidade, caso 3 técnicos não gostem de nenhuma atividade se teria o total de 35 técnicos)
-
Como não sabemos a intersecção, vamos chamar de X. Assim,
Atividade I e II: X
Atividade I: 29-x
Atividade II: 28-x
29-x + 28-x + x = 35
Resolvendo... +x-x corta. Resta...
29-x+28=35
X = 22
-
Total de técnicos=35
Atividade 1= 29
Atividade 2= 28
29 + 28 = 57
57 - 35 = 22 Intersecção
-
X = CORRESPONDE A INTERSEÇÃO ENTRE A ATIVIDADE 1 E A ATIVIDADE 2 = quantidade mínima de técnicos desse grupo que gostam das duas atividades .
ATIVIDADE 1 = 29 - X
ATIVIDADE 2 = 28 - X
INTERSEÇÃO = X
SOMA-SE TUDO E TEM QUE RESULTAR EM 35 QUE CORRESPONDE AO Nº TOTAL DE TÉCNICOS
29-X +28-X +X = 35
X= 22
22 É MAIOR QUE 20 A RESPOSTA É CERTO
-
X = CORRESPONDE A INTERSEÇÃO ENTRE A ATIVIDADE 1 E A ATIVIDADE 2
ATIVIDADE 1 = 29 - X
ATIVIDADE 2 = 28 - X
INTERSEÇÃO = X
SOMA-SE TUDO E TEM QUE RESULTAR EM 35 - 4 QUE CORRESPONDE AO Nº TOTAL DE TÉCNICOS MENOS OS 4 técnicos desse grupo não gostam de nenhuma das atividades citadas,
29-X +28-X +X = 35 -4
29 +28 -X = 31
57 - X = 31
X = 26 --> mais de 25 técnicos gostam das duas atividades. CORRETO
-
o máximo que não gostam das 2 atividades so pode ser até 5
-
Certo.
22 gostam das duas
6 (II) gosta de somente uma
7 (I) gosta de somente uma
quantidade mínima que não gostam das duas são 6.
quantidade máxima que não gostam das duas são 7.
-
Certo.
28+29+4=61
61-35=26 (intercessão)
(II)=28-26=2
(I)=29-26=3
Conclusão: se 4 não gostam então 26 gostam das duas
-
Eu raciocinei assim: se 29 gostam da I, e 28 gostam da II, tem-se, com certeza que, no mínimo, 29 pessoas gostam de pelo menos uma das atividades. É o que dá pra concluir com precisão.
Ao contrário de alguns colegas aqui que disseram que o conjunto máximo de pessoas que não gostam de nenhuma atividade é igual a zero, eu penso que não, pois não tem como nós sabermos se realmente as 35 pessoas gostam de pelo menos uma atividade. Não dá pra termos certeza.
Pode ser que, das 35 pessoas, todas gostem de pelo menos uma das atividades. Mas pode ser que NÃO, ou seja, que algumas não gostem de nenhuma das atividades.
LOGO, o MÁXIMO de pessoas que pode não gostar de nenhuma é:
De 29 a 35 temos 6. Portanto, pode ser que ATÉ 6 PESSOAS não gostem de nenhuma das duas atividades.
Gabarito: correto (6 é inferior a 7)
-
35 - 4 = 29 + 28 - x
31 = 57 - x
x = 26 gostam das duas atividades
-
Exceto o Raphael, esqueceram dos que não gostam das atividades. O correto seria: 35 - NGOSTAM = 29 + 28 - AMBOS; AMBOS = 22 + NGOSTAM. Então, mesmo que aumente os que NGOSTAM, AMBOS também aumentaria, sendo sempre superior a 20.
-
Fazendo essa questão por diagrama temos:
29-x+x+28-x+4=35
61-x=35
-x=35-61
-x=-26
x=26 (questão certa, mais de 25 técnicos gostam das duas atividades)
-
Em qualquer conta: o nº máximo que pode ficar fora dos conjuntos é sempre o Total - o maior conjunto.
35 - 29 = 6. (Nessa questão, se você tirar + que 6.. não conseguirá formar o conjunto dos que gostam da atividade I)
Exemplo: 35 - 7 = 28 técnicos. ... a questão disse que 29 gostam da atividade 1, portanto faltaria 1.
-
35 técnicos - 4 (q não gostam de nada) = 31. 31 - Técnicos dentro dos conjuntos de A 1 e A 2.
29 A.1 + 28 A.2 = 57 - 31 = 26. 26 - São os técnicos que gostam simultaneamente de A1 e A2.
Gabarito: Correto.
-
Segundo o Professor Josimar Padilha, tudo que extrapolar o meu universo será a INTERSEÇÃO
Então: 29+28= 57
57-35(meu universo)= 22 ,ou seja, superior a 20
ITEM CORRETO
-
Tenho essa e outras questões, além de aulas teóricas, resolvidas em vídeo. Acesse http://www.tutorraciociniologico.com.br/
-
Tenho essa e outras questões resolvidas em vídeo. Acesse tutorraciociniologico.com.br
-
Gente, o bizu da Patrícia Agostinho é show!!! Ganharemos tempo na prova.
Persevere. Vc não pode desistir agora!
-
(29 - x) + x + (28 - x) = 35
X = 57 - 35
x=22
GAB. CERTO
-
Construindo o diagrama de Venn abaixo:
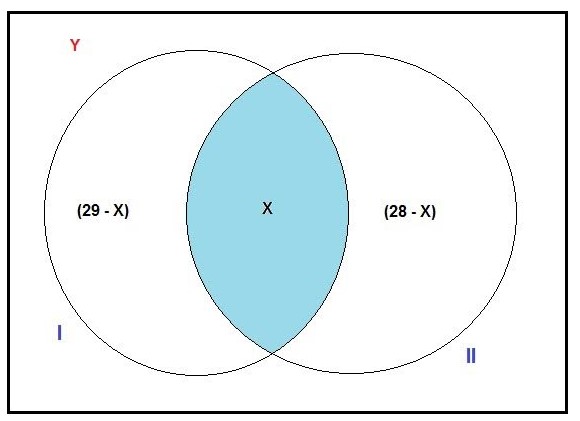
Montando-se agora a equação com o diagrama acima:
Y + (29 - X) + X + (28 - X) = 35 (total no grupo)
Resolvendo
Y = X + (35 - 57)
Y = X - 22
Assim para sabermos a quantidade máxima de técnicos desse grupo que não gosta de nenhuma das atividades, basta acharmos o valor máximo que a variável "X", pode atingir.
Para sabermos esse valor, basta olharmos o diagrama de Venn, no conjunto II (O menor conjunto) . Ali vemos que o maior valor que "X" pode atingir é 28, qualquer valor acima deste, o conjunto II ficará com elementos negativos, o que não pode acontecer, assim:
Y = 28 - 22
Y = 6
Resposta: CERTO
-
Rafael PST, ou outra pessoa não consegui chegar ao resultado 22, preciso de ajuda. obrigado
-
Esse lance de fazer diagrama com um monte de X também não funciona comigo amigo. Seguinte. Neste caso, a quantidade mínima de técnicos desse grupo que gostam das duas atividades é, simplesmente, a interseção entre os conjuntos. Essa interseção pode ser obtida da seguinte forma. Total dos que gostam da atividade I (29) + Total dos que gostam da atividade II (28) - a quantidade de técnicos que participaram da pesquisa (35) = 22. (29 + 28 - 35 = 22).
-
A 1 = 29 - X
A 2 = 28 - X
Inter. = X ( Gostam das duas atividades)
Somamos tudo e igualamos a 35 (número total de técnicos)
29 - X + 28 - X + X = 35
29 - X + 28 = 35 (cortamos o "- X" com o "+ X")
- X + 57 = 35
- X = 35 - 57
- X = - 22 (*-1)
X= 22
22 > 20 = CERTO
-
A 1 = 29 - X
A 2 = 28 - X
Inter. = X ( Gostam das duas atividades)
Não gostam de nenhuma = 4
Somamos tudo e igualamos a 35 (número total de técnicos) - 4 (técnicos que não gostam de nenhuma)
29 - X + 28 - X + X = 35 - 4
29 - X + 28 = 31 (cortamos o "- X" com o "+ X")
- X + 57 = 31
- X = 31 - 57
- X = - 26 (*-1)
X= 26
26 > 25 = CERTO
-
Só uma questão, em que momento do enunciado ele disse que os entrevistados gostavam "necessariamente" de uma das duas atividades????
Ou seja, você adivinha e supõe que não havia nenhum que não gostava de nenhuma das 2 atividades e faz a questão....
Sei lá ! Em se tratando de CESPE poderiam facilmente considerar o item errado!
-
Sinceramente tem gente que faz umas contas loucas que eu não entendo nada. Quanto mais simples melhor
O jeito que fiz foi assim.Muito fácil e rápido.
Pega os numero: 29(I), 28(II), e 4(é o que ele dá na questão) e 35 que é meu Universo
Resolução: 28+29+4 = 61
61-35= 26 ou seja maior que 25
-
Bom dia! Percebo que há uma outra possibilidade de montar um diagrama de Venn em que a atividade II esteja totalmente contida na atividade I. Dessa forma, teremos 28 em II contido em I; em I haverá apenas 1 pessoa (28 + 1 = 29, que é o número de elementos do conjunto I) e portanto, por "fora", ou seja, que não gostam de nenhuma das duas atividades, há 6 pessoas. Somando tudo teríamos os 35 (28 + 1 + 6 =35).
É uma maneira válida de montar o diagrama também!
Além da maneira de considerar a interseção com 22 pessoas como já exposto pelos colegas.
Assim, do jeito que demonstrei, "Infere-se dos dados que a quantidade mínima de técnicos desse
grupo que gostam das duas atividades é superior a 20", a resposta é certa; pois temos 28 pessoas que gostam das duas atividades.
Bons estudos e persistamos, Natália.
-
Bom dia! Percebo que há uma outra possibilidade de montar um diagrama
de Venn em que a atividade II esteja totalmente contida na atividade I.
Dessa forma, teremos 28 em II contido em I; em I haverá apenas 1 pessoa
(28 + 1 = 29, que é o número de elementos do conjunto I) e portanto,
por "fora", ou seja, que não gostam de nenhuma das duas atividades, há 6
pessoas. Somando tudo teríamos os 35 (28 + 1 + 6 =35).
Assim, do jeito que demonstrei, "A quantidade máxima de técnicos desse grupo que não gosta
de nenhuma das duas atividades é inferior a 7", a resposta é certa; pois temos 6 pessoas que não gostam de nenhuma atividade.
Bons estudos e persistamos, Natália.
-
Uma maneira simples de resolver essa questão é:
Se I=29 e II=28 sendo x a interseção, Então 29+28-x=35
29+28=57
57-x=35, 35-57= -x (multiplicando o resultado por -1) se tem 22
Logo questão correta :)
-
Muito facil fazer essas questões de conjunto.
-
Resolvendo de acordo com os dados do enunciado:
I = 29
II = 28
Chamando de x a interseção:
29 + 28 - x = 35
x = 22
Resposta: Certo
-
Galera, há outras questões do CESPE cobrando o mesmo raciocínio, vamos a ele: Quando no enunciado ele diz que há 29 que gostam da atividade I e 28 da atividade II, qual seria o "pior" cenário? Que todos os que gostam da atividade II estivessem dentro do conjunto dos que gostam da atividade I, assim, somente 1 pessoa gostaria somente da atividade I enquanto os 28 gostariam da atividade I e II ao mesmo tempo. Conclusão, sendo essa a situação que potencializaria a quantidade de pessoas que não gostam de nenhuma atividade, se fizermos as contas 35 - 29 = 6, logo, certa a alternativa.
-
29+28-30=22 e taca lhe pau.
-
Pensei igual a Patricia Agostinho, verificando a hipótese máxima , em que o conjunto II está inteiramente dentro do conjunto I, sobrariam 6, no máximo, para estar fora dos dois conjuntos..
-
Rock Lee, vc escreveu errado... 29+28 - 35 = 22. Abraços
-
Bem, na verdade acho que o correto mesmo seria:
total de pessoas => 35
Tarefa i => 29
Somente tarefa i => 29-x
Tarefa ii => 28
Somente tarefa ii => 28-x
onde x é os que participam das duas tarefas
TEMOS QUE ACRESCENTAR O NÚMERO DE PESSOAS QUE NAO PARTICIPAM DE NENHUMA DAS TAREFAS: n
N( i U ii ) = n(i) + n(ii) - n(i ^ II) OBS: veja que i uniao ii é o total de pessoas(35) menos os que não participam de nenhuma.
35 - n = 29 + 28 - x
35 - n = 57 - x
35 - n - 57 = -x
x = 57 - 35 + n
x = 22 + n =>> onde n = 0 para que consigamos o valor mínimo.
-
O comentário do professor RLM deixa a desejar heim! Deveria ser em vídeo, eu pelo ao menos estou entendendo o assunto, mas, e quanto aos outros!?
-
NÃO NÃO NÃO
,
cuidado aÍ galera!!!! EXISTE A POSSIBILIDADE DE UM TÉCNICO NÃO GOSTAR DE NENHUMA!!
Se discordarem, olhem as questões Q559939 e Q559940!!!
FAZENDO OS CÁLCULOS:
no diagrama fica:
técnicos que gostam SOMENTE de I = 29-x
técnicos que gostam SOMENTE de II = 28-x
técnicos que não gostam de nenhuma = n
x = intersecão de I e II
Equação
(29 - x) + (x) + (28 - x) + n = 35
desenvolvendo (...), temos que
x = 22 + n
Logo, COM TODA A CERTEZA DO MUNDO, podemos afirmar que o mínimo é 22.
Veja bem heim: n pode variar de 0 a 6 !!! explique-se:
o maior conjunto (daqueles que gostam de I) contém 29 pessoas. Logo, concluimos que n está em um intervalo de 0 a 6. Pense um pouquinho e entenderá o porquê. 35 - 29 = 6
A questão está DE FATO correta.
Cuidado, pois o cespe poderia colocar uma casca de banana aí.
qualquer coisa chama no inbox, pois tenho limite de ''acompanhamento de comentários''. rsrs
Bons estudos
-
Campanha para o qc colocar um professor pra resolver as questões em video.........
-
Todo mundo conclocando "não gostei" na resposta e explicando que QUEREMOS AULA EM VÍDEO. Porque não tem condições RLM sem ser em vídeo.
-
X -> Seja X os que gostam da I e II
35=29+28+4-X
35=61-X
X=-35+61
X=26
26>25
-
Tem um bizu do professor Jhoni do Focus Concursos que é assim(Vou tentar explicar sem imagem)
Primeiro: Esqueçam a palavra ''Máximo'' só tá ai pra atrapalhar!
Segundo: Toda vez que ele pedir o numero que não gasta de nenhuma das duas atividades, sem ter dado a INTERSECÇÃO. Vcs vão pegar o menor valor que ele deu (II - 28) e coloca na intersecção do conjunto.
Terceiro: Agora calcula: I - 29 - 28(Intersecção) = 1 / II = 0(Pq a intersecção já é 28) / Intersecção = 28 / Toral = 35
Quarto: 1 + 28 - 35 = 6. FIM.
SE VCS VEREM MONTADO NO CONJUNTO É BEM SIMPLES!!! NÃO DEMORA NEM 2 MINUTOS!!! AQUI FICA COMPLICADO FAZER. ABRAÇOS
-
Bem fácil essa. É só somar I + II, e subtrair do total: 29 + 28 - 35 = 22 (interesecção entre os dois grupos)
-
Vou tentar explicar:
atividade I --> 29 gostam da atividade I
atividade II -->28 gostam da atividade II
O pior cenário seria todos que gostam da atividade II e também gostar da atividade I.
Logo, sobraria apenas um que gosta somente da atividade I (29 - 28 = 1 gosta somente atividade I, os outros 28 gostam da atividade I e atividade II)
A pergunta é:
A quantidade máxima de técnicos desse grupo que não gosta de nenhuma das duas atividades é inferior a 7 ?
certo, pois considerando o pior cenário teriamos 29 que gostam de pelo menos uma atividade ( considerando 28 que gostam das 2 atividades + 1 que gosta somente da atividade I). Assim, 35 -29 = 6 que não gostam de nenhuma atividade ( 6 é menor do que 7).
Tentei explicar..
-
JULIO OPALOSKI, um número ser superior a outro é diferente de um número ser sucessor de outro.
-
Usa 31 no lugar dos 35 funcionários.
28+29 = 57
57 - 31 = 26
-
É fácil! Este item é complemento de outro da prova, veja:
1º achamos a intersecção - (TODOS - TOTAL) = ?
(29+28) - 35 = 22
Logo, 22 gostam das duas atividades.
2º Vamos encontrar em cada atividade os que ñ gostam de nada
(Atividade - Intersecção)=?
Atividade I =29
Atividade II =28
atv I (29-22) = 7
atv II (28-22) = 6
#DICA: 1º ENCONTREM A INTERSECÇÃO E APÓS DIMINUEM COM OS ITENS PEDIDOS.
Com esta fómula garantimos outros itens do Cespe.
-
X+29+28=35
X + 57 = 35
X = 57-35
X = 22
22+4 = 26
-
Basta resolver considerando que de fato 7 não gostam de nenhuma ativdiade. Fazendo o diagrama e as contas devidas a interseção dará igual a 29, com isso o conjunto I ficaria igual a zero e o dois igual a -1, tornando-se impossível 7 não gostarem de nenhuma atividade.
Total = 35 ;
Interseção entre I e II - x (29 - x) + x + (28 - x) + 7 = 35 ==> 64 - x =35 ==> x = 29
Conjunto I - 29 - x Conj I = 29 - 29 = 0
Conjunto II - 28 - x Conj II = 28 - 29 = -1 (Impossível) logo falso.
-
Pelo Diagrama = 29-x+x+28-x=35
União = 22
A = 7
B = 6
U = 22
Soma e dá 35 - 35 do total = zero, quer dizer que todos praticaram atividades, a questão não é nula...cuidado!
-
N(A U B) =N(A) + N(B) - N(A V B)
35 = 29 + 28 - N(A V B)
N (A VB) = 57-35 = 22
AGORA..É SO SUBTRAIR
29-22 = 07
28-22= 06
LOGO A RESPOSTA É 06
-
Quando a questão pedir o máximo do lado de fora dos diagramas, basta criar a maior interseção possível, assim estarei forçando o máximo de pessoas que eu puder para fora dele, logo encontrarei a quantidade máxima de pessoas que não gostam de nenhuma das atividades, ou seja, a quantidade máxima do lado de fora. Para que eu crie a maior interseção possível, basta inserir todos os elementos do diagrama de menor quantidade na interseção, que é o diagrama da "atividade 2", que contém 28 pessoas. Logo, terei 28 pessoas na interseção. Como na "atividade 1" contém 29 pessoas, então apenas 1 pessoa estará somente na "atividade 1", subtraindo o real (35) pelo diagrama de maior quantidade de elementos (29), que é a "atividade 1", restará 6 que é a quantidade máxima possível de pessoas do lado de fora...
Logo a resposta será 6, ou seja, é infeior a 7. Gab: CORRETO
Um método mais rápido para não precisar trabalhar com incógnitas e nem fazer muitas contas... Saibam que há métodos para saber o "mínimo possível na interseção", o "máximo possível na interseção" e o "máximo possível do lado de fora dos diagramas" sem necessidade de cálculos com incógnitas...
Espero ter ajudado
Bons estudos a todos...
-
Se 29 já gostam do cargo I (mais que os 28 que gostam do cargo II) e são 35 no total, então só resta 6 para não gostar de nenhum; pois basta gostar de qualquer um dos cargos para não entrar no conjunto dos que não gostam de nenhum.
-
Construindo o diagrama de Venn abaixo:
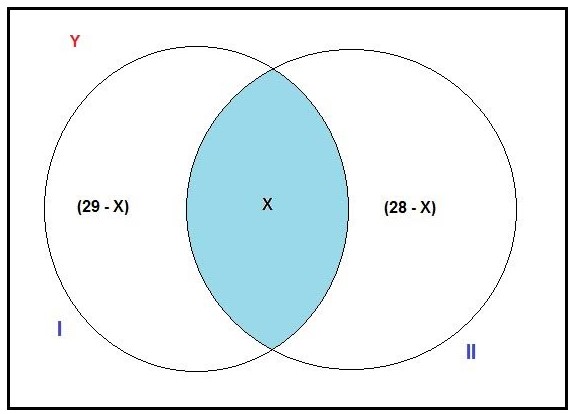
Montando-se agora a equação com o diagrama acima:
Y + (29 - X) + X + (28 - X) = 35 (total no grupo)
Resolvendo:
Y = X + (35 - 57)
Y = X - 22
Assim para sabermos a quantidade máxima de técnicos desse grupo que não gosta de nenhuma das atividades, basta acharmos o valor máximo que a variável "X", pode atingir.
Para sabermos esse valor, basta olharmos o diagrama de Venn, no conjunto II. Ali vemos que o maior valor que "X" pode atingir é 28, qualquer valor acima deste, o conjunto II ficará com elementos negativos, o que não pode acontecer, assim:
Y = 28 - 22
Y = 6
Resposta: CERTO
-
Entendi assim:
Para descobrir a intersecção faça: 29+28-35 = 22 (intersecção)
Gostam somente da atividade I: 7
Gostam somente da atividade II: 6
Valor máximo que posso ter na minha intersecção: 28 pessoas, como cheguei a esse valor? Peguei 6 pessoas da atividade I e 6 da atividade II e somei apenas 22 + 6 = 28(nova intersecção). Conclusão depois disso:
Gostam somente da atividade I: 1
Gostam somente da atividade II: 0
Logo o valor máximo de técnicos desse grupo que não gosta de nenhuma das duas atividades é 6.
MANTENHA-SE FIRME! SEU NOME NO D.O.U.
-
Fiz sem procurar incognita, e acho que muitos aqui também. Enfim, minha resolução:
soma ativ 1 e ativ 2: 29+28= 57
subtrai o universo com o número que a questão ta pedindo: 35-4= 31
agora pra saber a interseção subtrai interseção com universo: 57-31= 26
creio que 26 é maior que 25, logo, questão correta.
-
É so fazer a conta de conjuntos como se estivesse 7 pessoas fora... percebe-se que 7 -35 é "28" e a questão me diz que "29" GOSTAM DA I,
logo no mínimo para que fique 29 para ser distribuídos entre os que gostam de pelo menos UM tem que 6 NO MÁXIMO NÃO GOSTAREM DE NENHUM...
Valeu.. Deus os Abençoe....
-
Essa foi tranquila....
-
Pra quem não entende muito bem esse tipo de questão, https://www.youtube.com/watch?v=Ia-slXgm1MA
-
29 -x+x+28-x+4=35
57-x+4=35
-x+61=35
x=35-61
x=26
Gabarito: Correto.
-
29 -x+x+28-x+4=35
57-x+4=35
-x+61=35
x=35-61
x=26
Gabarito: Correto.
-
carlos vlw pela dica mas, vi esse video que era o proximo https://www.youtube.com/watch?v=R4XeRZ0f0g8 ,e o prof. é muito melhor, para quem precisa de ajuda recomendo dar uma olhada vai aprender bem rapido.
-
Verdade Carlos! Fiquemos espertos!!! =)
-
-
CERTO
Considerando:
A: quem gosta da atividade I somente/ B: interseção (quem gosta da atividade I e II ao mesmo tempo)/ C: quem gosta da atividade II somente/ D: quem não gosta de nada.
Se o total de participantes da pesquisa = 35, logo:
A+B+C+D=35
A+B=29 (todos que gostam da atividade I).
Substituindo:
29+C+D=35
C+D=35-29
C+D=6
Se a soma de quem gosta apenas da atividade II com quem não gosta de nada é 6, então podemos garantir que o total de pessoas que não gosta de nada é < 7.
-
R: Certo
Veja a resolução do professor Josimar Padilha:
https://www.youtube.com/watch?v=Md0t5M2yMjU
-
Desde quando 7 é inferior a 7?
-
Não sei se o meu raciocínio está certo, mas fiz assim, se 29 gostam de I e 28 de II, subritai-se o 35 pelo 29, pois este é o maior nº, ou seja, de 35, 29 eu sei que gosta de alguma coisa, logo restaram 6 para gostarem das duas atividades I e II, ou para nenhuma delas. Neste caso, será 0 ou menor que 6, logo a questão está certa e a quantidade máx é inferior a 7 para as duas, pois o que quero é só acertar a questão, por isso não me importei tanto em achar quem ficou na interseção ou fora dela.
-
Essa foi só para esquentar... Falar assim é fácil, depois de estudar a matéria por horas... Acordei muito tarde para concursos, eu não tinha idéia de muitos aspectos que estou aprendendo, até mesmo descobrir RLM. Esse site tem sido uma excelente ferramenta.
-
se todos que gostarem de II também gostarem de I , a intersecção de ambos fica 28. assim, quem gosta somente de I seria apenas 1 (28+1=29). logo, o maximo de pessoas que podem nao gostar de ambos é 35-29=6.
-
Simplificando, o máximo de pessoas que podem gostar de algo, é 29, ou seja, tira os 29 do total de people, que são 35 e resta 6.
Certa. =/
-
A quantidade máxima de pessoas que podem gostar de algo é 29 (o grupo maior). Logo se foram 35 entrevistados, para responder a pergunta basta subtrair de forma simples 35 - 29 que dá 6.
Certa.
-
Uma pesquisa realizada com um grupo de 35 técnicos do MPU a respeito da atividade I — planejamento estratégico institucional — e da atividade II — realizar estudos, pesquisas e levantamento de dados — revelou que 29 gostam da atividade I e 28 gostam da atividade II. Com base nessas informações, julgue o item que se segue.
A quantidade máxima de técnicos desse grupo que não gosta de nenhuma das duas atividades é inferior a 7.
Pessoal do QC, a questão está incompleta!
-
Maneira mais simples possível:
Gosta da atividade I = 29
Gosta da atividade II = 28
Número máximo de técnicos que não gosta de nenhuma das 2 = ?
Os que não gostam de nenhuma das 2 pode ser no máximo 35 - 29 = 6, pois se 29 já gostam da atividade I, o máximo possível que não gosta de nenhuma das duas atividades é 6.
GABARITO: CERTO
Bons estudos galera ..
-
Fabiana Tomassoni acho que não hein...
-
CERTO
-
Thigo Silveira , fiz os cálculos tudo certinho e fiquei sem entender porque errei. Só depois de ler seu comentario eu entendi.
-
Tem muito comentário errado!! CUIDADO
A forma correta de resolver é se fazendo a pergunta, "No pior caso, qual a quantidade máxima de pessoas que não gostariam de nenhum do casos I e II?"
Pense que: 29 gostam de I e 28 gostam de II, o pior caso é se os 28 estiverem incluídos nos 29.
Calculando temos que se 35 - 29 = 6
6 pessoas podem NÃO gostar de nenhum do itens I e II
-
Resolução simplificada sem mimimi:
Total técnicos = 35
Gostam da atividade 1 = 29 - """""O segredo está em entender que a banca não restringiu, ou seja, 28 podem gostar de executar a atividade 1 e 2 ao mesmo tempo"""""
Gostam da atividade 2= Não restringiu ou seja este grupo de 28 pessoas podem gostar da atividade 1 e 2 ao mesmo tempo.
Resolução:
Atividade 1 e 2 = 28 pessoas
Somente atividade 1 = 1 pessoa
Somente atividade 2 = 0 pessoas
Não gosta de 1 nem de 2 = 35- 29(28+1+0) = 6 pessoas
Conclusão: O grande segredo é achar o numero "magico" da intersecção que atenda os dois critérios que são: 29 gosta da atv. 1 e 28 gosta da atv.2
-
Pelo Princípio da Inclusão-Exclusão temos a seguinte fórmula: n(A ∪ B) = n(A) + n(B) − n(A ∩ B).
Considerando A = atividade I e B = atividade II, temos:
n(A ∪ B) = n(A) + n(B) − n(A ∩ B)
35 = 29 + 28 − n(A ∩ B)
n(A ∩ B) = 22
Com isso, temos que:
7 técnicos gostam apenas da atividade I e 6 técnicos gostam apenas da atividade II.
Não há técnicos que não goste de nenhuma atividade.
Então, como 0 < 7, a resposta da assertiva é CERTO.
-
Minha contribuição.
Diagramas de Venn
Total de técnicos = 35
Atividade 1 = 29
Atividade 2 = 28
29 + 28 = 57
57 - 35 = 22 Intersecção
Apenas atividade 1 = 7
Apenas atividade 2 = 6
22 + 7 + 6 = 35
A quantidade máxima de técnicos desse grupo que não gosta de nenhuma das duas atividades é inferior a 7, pois é zero.
Abraço!!!
-
Acho que poderíamos considerar uma intersecção com valor 28 (número de II)
Poderia ser que 28 gostam de I e II e 1 que sobra (dos que gostam de I) = 29
35 - 29 = 6
No máximo 6 pessoas podem não gostar de nenhuma das atividades.
É uma ideia, não sei se foi coerentemente aceitável
-
CEERTO
Não existe nenhum funcionário que não goste de realizar nenhuma das duas tarefas.
a resposta é 0 que é inferior a 7.
-
Muitos comentários divergentes, mas acredito que o correto é a resolução do professor. Confiram.
-
E vamos de interpretação kkkkk Rindo p não chorar
-
Acertei a questão, porém estou abismado com ela; verdade é que 0 < 7, mas dá um frio na barriga para confirmar isso.
-
Não acho que a interseção seja 22, até porque pra ser 22 temos que considerar que TODOS gostam da atividade e na questão não fala isso, ela quer saber justamente o máximo de pessoas que NAO gostam de alguma atividade
EU fiz assim: Considerei o máximo de pessoas, que no caso seria 29, portante 35 - 29 = 6 seria o máximo de pessoas que poderiam nao gostam de alguma atividade!
-
Ótima explicação:
https://www.youtube.com/watch?v=DSVpZCMIHkc&ab_channel=NEAFConcursos
-
CERTO.
Não é necessário calcular interseção.
A questão informa que, dentre os 35 técnicos, 29 gostam pelo menos da atividade I (se eles gostam de I e II não interfere em nada).
Desse modo, se eu já tenho certeza de que 29 gostam de pelo menos uma das atividades, o máximo de pessoas que poderia não gostar de nenhuma delas é 35 - 29 = 6.
Em questões como essa basta subtrair: Valor total - Valor do maior conjunto.
-
Gabarito:Certo
Principais Dicas:
- Principais questões são de 2 ou 3 conjuntos.
- Primeiro acha sempre a intersecção e sai complementando. Ex: A ∩ B = 10; A= 20; B=30. Logo, A tem apenas 10 e B tem apenas 20.
- Caso não tenha a intersecção? Soma tudo e subtrai do total. Ex: A= 20; B=30; Total= 40. Logo, a intersecção é 50-40=10.
- E cuidado nas questões que ele fala APENAS, SOMENTE etc.
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
-
Prezados, gabarito incorreto. Deixarei a correção da questão feita pelo professor Josimar Padilha do Gran Cursos Online.
https://www.youtube.com/watch?v=Md0t5M2yMjU
BONS ESTUDOS.
-
0 a resposta. Menor que 7
-
Sem complicação, devemos fazer assim, incluir todos do grupo II dentro do grupo I, é a maneira correta de fazer, sendo assim, sabemos que todos do grupo II também gostam da atividade do grupo I, como no grupo I contém 29 técnicos, supomos que apenas 1 gosta da atividade I, e os demais gostam das duas atividades, sendo assim, para compor o total, descobrimos quantos estão fora, que seriam 29 + 6 que não gostam de nenhuma das duas atividades, que fica o total correto de 35 técnicos.
-
ZERO É REALMENTE INFERIOR A 7. COMO ERREI ISSO? KKKKKKKKKKKKKKKKKKKKKK
-
Certo, pena que esse tipo de questão não cai mais ao menos nas carreiras policiais n
-
Certo
(quem não gosta de nenhuma das duas atividades) y
(interseção) x
29 - x + x + 28 - x + y = 35
29 + 28 = 57 - x + y = 35
57 - 35 + y = x
22 + y = x ou x = 22 + y
O valor da intersecção pode ser 22, não é exato.
• O valor de x é superior a 20?
• O y, na pior das hipóteses, pode ser = 0
• Se o y for 0, x = 22.
• Se o y for 1, x = 23
• Se o y for 2, x = 24
• Qual o maior que y poderá assumir?
• É inferior a 7?
x = 22 + 7
x = 29
29 - 29 = 0
28 - 29 = -1
• O y não pode ser 7, porque não tem como o resultado ser negativo.
• E se for inferior a 7 (testar o 6)
x = 22 + 6
x = 28
29 - 28 = 1
28 - 28 = 0
• se o y for 5?
x = 22 + 5
x = 27
29 - 27 = 2
28 - 27 = 1
Prof Márcio Flávio
-
Ufaaaa! Estava quebrando a cabeça com os outros comentários.
Obrigada :)
-
Pessoal comentando que zero é menor que 7... Cuidado!
A questão quer saber o número máximo de pessoas que não podem gostar somente da disciplina II.
Dessa forma, se a intersecção for = 28 (22 + 6, (primeiro número menor que 7)), então 1 pessoa gosta da disciplina I e 0 gostam SOMENTE da ii.
https://sketchtoy.com/70400367
Gaba: C