-
Gabarito da questão é "D". Site da banca : http://www.upenet.com.br/
-
Fiz tudinhoooo....minha resposta foi D....onde está o erro? No site Qconcurso ou na própria prova?
-
Rosimeire ocorreu a mesma coisa comigo, acho que o erro é do qconcurso e não nosso! :-D
-
Também achei a D.
-
Gente...também cheguei a conclusão da letra D....Qconcurso e agora? Assim confunde a nossa cuca.
-
Fiz todas na tabela verdade e as alternativas B e D ambas não são tautologia.
-
Duas questões não são tautologias: Letras C e D
-
Pessoal notifiquei o erro e recebi a resposta de que analisaram a questão. Agora consta correta a alternativa D...Obrigada Qconcursos pela atenção.
-
Eu fiz todas as tabelas verdade e a resposta é mesmo a letra D.
Se alguém tiver uma dica ou macetes em equivalências.... manda aí!
-
Confusa!
-
A minha foi resposta A - (A^B) -.> (AvB).
-
Pessoal, eu não entendi esta questão! Alguém poderia me ajudar, por favor?
-
Vitor Costa olha como fica fácil quando fazemos o inverso que a questão pede. Exemplo: ela fala em tautologia e tautologia sempre será V, então escolhemos os valores de A e B falsos, o inverso.
Se A=F, B=F, logo: ~A=V, ~B=V
a) (A ∧ B) → ( A ∨ B)
(F ∧ F) → (F V F) =
F→F=V ERRADO! Deu V no final e não estamos buscando a tautologia.
b)~ ( A ∨ B) → (~ A ∨ B )
~(F V F) → (V V F) =
~(F) → V =
V → V = V ERRADO
c)(A ∧ ~ B) → ~ ( A ∧ B )
(F ∧ V) → ~ ( F ∧ F ) =
F → ~(F) =
F → V = V ERRADO
d)( A ∧ B ) ∨ ( ~ B → A )
(F∧ F ) ∨ ( V → F ) =
F V F = F CORRETO
e)A ∨ ~ A
F V V= V ERRADO
-
O queme salva é fazer a tabela básica, colocar mais uma coluna para ~A e outra para ~B, e por fim ir cruzando os resultados um a um. Demora, mas da certo.
-
Construindo a tabela-verdade para cada item:
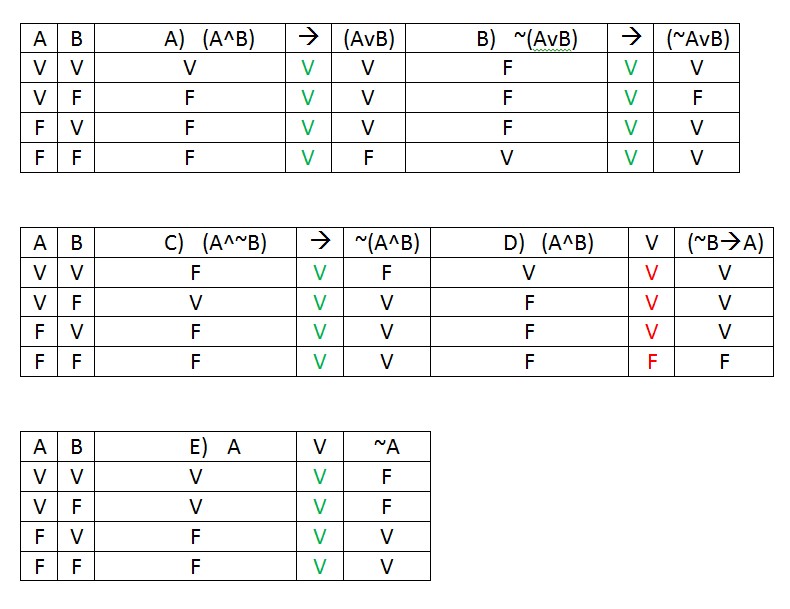
Resposta: Alternativa D.
-
Natalie Silva : obrigado , entendi!
-
A banca estabeleceu A v B com uma disjunção inclusiva e não exclusiva o que muda o valor lógico de uma linha da tabela. Se você considerou como disjunção exclusiva, acabou por marcar a alternativa a como gabarito.
Lembrando que numa prova muitas vezes não temos tempo para resolver toda a tabela....
-
Gabarito letra d).
Antes de responder à questão, deve-se saber as seguintes informações:
1) A operação conjunção ("e"/∧) só é verdadeira quando todas as proposições são verdadeiras.
2) A operação disjunção ("ou"/"∨") só é falsa quando todas as proposições são falsas, ou seja, basta uma ser verdadeira para a sáida ser verdadeira.
3) Na condicional ("→"), a saída só será falsa se a condição suficiente for verdadeira e a condição necessária falsa. Se der V seta F, então saída falsa (V → F).
DICA: SE DER "VERA FISCHER", ENTÃO SAÍDA É FALSA.
4) Ocorre tautologia quando todas as saídas são verdadeiras.
QUESTÃO
A B ~A ~B A ∧ B A ∨ B ~(A ∨ B) ~A ∨ B A ∧ ~B ~(A ∧ B) ~B → A
V V F F V V F V F F V
V F F V F V F F V V V
F V V F F V F V F V V
F F V V F F V V F V F
(A ∧ B) → (A ∨ B) ~(A ∨ B) → (~A ∨ B) (A ∧ ~B) → ~(A ∧ B) (A ∧ B) ∨ (~B → A) A ∨ ~A
V V V V V
V V V V V
V V V V V
V V V F V
* A expressão "(A ∧ B) ∨ (~B → A)" não é uma tautologia, pois possui uma saída falsa. Caracterizando-se, portanto, uma contingência, e não uma tautologia.
=> Meu Instagram para concursos: https://www.instagram.com/qdconcursos/
-
Tabela verdade neles!
-
Na minha opinião, a melhor forma de se resolver questões dessa natureza é tentar provar que a sentença poderá NÃO ser tautologia em algum momento. Vejamos os exemplos da alternativa A e a D, respectivamente:
a) (A ∧ B) → ( A ∨ B)
v v v v
v → v
Verdadeiro!
Após, TENTANDO demonstrar que uma das proposições será falsa:
a) (A ∧ B) → ( A ∨ B)
v f v f
f → v
Verdadeiro!
Perceba que ainda assim a alternativa continua sendo verdadeira, posto que a alternativa só será falsa se as proposições forem V e F, respectivamente. Logo, temos uma tautologia e consequentemente a questão está errada!
Agora, resolvendo O GABARITO, teremos o seguinte:
d) ( A ∧ B ) ∨ ( ~ B → A )
v ∧ v ∨ f → v
v ∨ v
Verdadeiro!
Após, TENTANDO demonstrar que uma das proposições será falsa:
d) ( A ∧ B ) ∨ ( ~ B → A )
v ∧ f ∨ v → f
f ∨ f
Falso! ---> ENCONTRAMOS A RESPOSTA!!!
Espero ter ajudado!!!