-
Resolução:
PETROBRAS possui 9 letras. As duas primeiras ficarão fixas, restando apenas a permutação das outras 7 letras que restaram.
P(7 letras) = 7!
Contudo, a letra "R" está se repetindo 2 vezes. É necessário, portanto, dividir o resultado da permutação das 7 letras pelo resultado da permutação das demais letras que se repetem:
P(2) = 2!
Logo, temos:
P(7) = 7! / 2!
P(7) = 2.520
-
Complementando o comentário muito bom do colega Thiago Alves
Para se obter o número de anagramas possíveis a partir das letras de determinada palavra, desde que não tenham letras reptidas, basta fazer a permutação (P) com o número total de letras, ou seja: > Seja 'n' o número de letras de determinada palavra e Na o número de anagramas, temos:
> Na = P(n) = n!
(note-se que, por este método, muitas combinações de letras não formarão palavras)
Exemplo: Quantos anagramas obtém-se da palavra "daniel"? > Resposta: daniel tem 6 letras, portanto, n=6;
> Na = P(6) = 6! = 6x5x4x3x2x1 = 720 anagramas
Caso tenhamos letras repetidas na palavra, devemos dividir o resultado de P(n) pelas permutações de cada letra repetida. Seja r1 e r2 a quantidade de respetições de 2 letras distintas de determinada palavra, temos: > Na = P(n)/(P(r1) x P(r2)) = n!/(r1! x r2!)
Exemplo: Quantos anagramas obtém-se da palavra "paralelepipedo"? > Total de letras: n=14
> Número de repetições:
letra 'p' = 3 repetições;
letra 'a' = 2 repetições;
letra 'l' = 2 repetições;
letra 'e' = 3 repetições;
Portanto: Na = P(14)/(P(3) x P(2) x P(2) x P(3));
Na=14!/(3! x 2! x 2! x 3!);
Na=14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3!/(3 x 2 x 2 x 2 x 3!);
Na=(14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4)/(3 x 2 x 2 x 2);
Na = 605.404.800 anagramas
-
Este não fui eu quem resolvel. Mas ajuda muito para quem não entende (Assim como eu)
Anagramas é um tipo, uma relação, um jogo com as letras das palavras. Ou seja, formas de misturar as letras formando outras palavras (existente e com sentido ou inexistente e sem sentido). Todo mundo já brincou de fazer anagrama com o próprio nome, nem que seja escrevendo de trás para frente, para ver como fica.
Pegando uma palavra simples: ELO. Os anagramas possíveis são:
ELO
EOL
LEO
LOE
OEL
OLE
São 6 anagramas possíveis com a palavra ELO. Para sabermos o número de anagramas possíveis de uma palavra é simplesmente o número de letras (N) fatorial.
No caso 3! = 3×2 = 6 anagramas.
Mas temos o caso especial, quanto há repetições, no caso de ASa (vou escrever com um a minúsculo para diferenciar os “a’s”.
O anagrama ASa e aSA são iguais e não contariam como 2 anagramas diferentes, afinal formaram a mesma palavra. Então para sabermos o número de anagramas quando se tem letras repetidas, se faz N!/Repetições!, nesse caso seria 3!/2! = 3. Sendo os anagramas:
AAS
SAA
ASA
Agora vamos para a questão, que obviamente você nunca irá ser tão fácil quanto os exemplos
Ela quer os anagramas da palavra PETROBRAS, mas dá uma condição: tem que começar com PE e nessa ordem. Ou seja, o PE nunca vai sair do lugar dele. Então basta esquecermos ele no começo e fazer o anagrama do resto, fazemos apenas o número de anagramas do TROBRAS.
Temos 7 letras, sendo 2 repetidas:
7!/2! = 7x6x5x4x3x2/2 = 2.520
RESPOSTA LETRA B
-
As duas palavras "P" e "E" nesse caso permanecem juntas, como se fossem um bloco, assim temos um total de 7 letras para permutarmos, sendo que das 7 letras restantes, a letra "r" repete duas vezes, assim temos uma permutação com repetição:
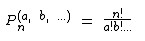Logo n = 7 e a1 = 2:
P7,2 = 7!/2! = 2.520
Resposta: Alternativa B.
-
A palavra possui um total de 9 letras (n = 9), sendo que possui 2 letras R (r = 2).
1 * 1 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5.040 possibilidades
P E
Porém, como existem duas letras repetidas deve-se dividir 5.040/2! = 5.040/2 = 2.520.
-
Mas a divisão é por 2, dos dois R , ou por 2!? E se no caso fossem três letras repetidas?
-
Tenho uma dúvida :
Por que as letras P e E não contam como sendo uma unidade ? Tal qual acontece nesse caso :
"Qual é o número de anagramas da palavra TRANSPETRO em que as letras PETRO ficam juntas e nessa ordem?"
-
Respondendo ao amigo Paulo Silva, por apenas um detalhe Paulo, o exercício acima pediu que as letras P E ficassem nessa ordem e não juntas e nessa ordem como no caso da T R A S PETRO que pediram juntas e nessa ordem.
Na questão acima ficou assim.
1 x 1 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040
Mas como a letra R repete duas vezes dividimos por 2
5040 / 2 = 2520
-
PETROBRAS 9 LETRAS
TIRANDO O PE, RESTAM 7, LOGO:
TROBRAS = 7! = 7X1X2X3X4X5X6 = 5040
PE = 2! = 2X1 = 2
7! / 2! = 2520