-
A: n° inteiro é par
B: quadrado do n° inteiro é par
-
Pelo enunciado do problema: A<=>B = (A=>B)^(B=>A)
-
Pois bem. É preciso encontrar uma nova equivalência para A<=>B. Para tanto, vamos investigar (A=>B) e (B=>A), a partir de suas tabelas-verdade:
----------------------------------
A|B|A=>B|B=>A|~A|~B|~A=>~B|~B=>~A|
----------------------------------
V|V| V | V |F |F | V | V |
V|F| F | V |F |V | V | F |
F|V| V | F |V |F | F | V |
F|F| V | V |V |V | V | V |
----------------------------------
Comparando os resultados, obtém-se:
B=>A = ~A=>~B
portanto: A<=>B = (A=>B)^(~A=>~B)
-
p: um número inteiro é par.
q: seu quadrado é par.
----
Então vejamos: p ↔ q
Equivalência: ( ¬ p V q ) ^ ( ¬ q V p). Essa é a equivalência que pensaríamos em primeiro plano, mas não existe resposta para tal.
Vejamos: a equivalência da disjunção “OU” pode ser o condicional: negando a condição suficiente e confirmando a condição necessária:
( p → q ) ^ ( q → p).
Ainda não há resposta para esta equivalência. Porém o condicional aceita duas formas de equivalência e uma delas é a contrapositiva: nega a condição necessária, então nega a condição suficiente. Vamos utilizar esta equivalência apenas para o segundo termo:
( p → q ) ^ ( ¬ p → ¬ q )
------
Sucesso a todos.
-
Basta saber que p <----> q é equivalente à p--->q ^ q--->p
Sabemos que;
P:Número inteiro par
Q:Quadrado é par
Analisando o enunciado
"Um número inteiro é par se e somente se o seu quadrado for par" P <-----> Q
Logo Analisemos o seguinte
P <---->Q é equivalente á P--->Q ^ ~P--->~Q ( Alternativa a), uma vez que ~P---> ~Q é equivalente a Q---->P
-
O conectivo se e somente se pode ser entendido como uma "bicondicional", ou seja, uma dupla "condicional". Então podemos converter essa proposição em uma dupla "se...então":
"um número inteiro é par se e somente se o seu quadrado for par"
Se um número inteiro é par, então o seu quadrado é par, e, se o quadrado de um número é par, então o número inteiro é par.
Veja que não existe nenhuma alternativa com esta frase. Mas esta é uma frase equivalente! Só não está na questão. Vamos adaptá-la à resposta. Veja que a segunda parte é uma condicional:
"Se o quadrado de um número é par, então o número inteiro é par"
Usando uma das equivalências da condicional, a (p -->q) <==> (~q -->~p), ou seja vamos inverter e nagar as partes na condicional:
"Se o número inteiro não é par , então o quadrado não é par "
Então juntando com a primeira parte, temos:
Se um número inteiro é par, então o seu quadrado é par, e, se um número inteiro não é par , então o seu quadrado não é par .
Alternativa A.
-
"um número inteiro é par se e somente se o seu quadrado for par"
Trata-se de uma proposição bicondicional, que tem como equivalente (p ---> q) ^ (q ---> p)
Ficaríamos então com a seguinte, proposição equivalente à primeira:
Se um número inteiro é par, então seu quadrado é par e se o seu quadrado é par, então o número é par.
Temos agora duas proposições condicionais:
p = Se um número inteiro é par, então seu quadrado é par; e
q = se o seu quadrado é par, então o número é par.
A letra a da questão está meio certo, já que trás a primeira parte do enunciado correto ("se um número inteiro for par, então o seu quadrado é par"). Precisamos somente saber se a segunda proposição equivale à do enunciado. Vamos achar sua equivalente.
O equivalente de uma proposição condicional é dado por ~q ---> ~p
trabalhando com a proposição q, temos sua equivalente como:
q = "se o seu quadrado é par, então o número é par" (proposição normal)
vamos encontra ~q ---> ~p
~q = o número não é par
~p = o quadrado do número não é par
Portanto, a letra a é correta, visto que é equivalente a expressão encontrada:
Se um número inteiro é par, então seu quadrado é par E se o número não é par, seu quadrado não é par
Resposta = a
-
A se e somente se B = (Se A então B) E (Se B então A)
Para facilitar vamos transformar as frases em letras:
A = "um número inteiro é par"
B = "o seu quadrado for par"
a) Traduzindo: (Se A então B) E (Se ~A então ~B)
Precisamos lembrar que "Se A então B" é equivalente à "Se ~B então ~A", ou seja, a equivalência do Se...então é "inverte e nega", no caso em questão, (Se ~A então ~B) é igual (equivalente) à (Se B então A).
Então podemos considerar: (Se A então B) E (Se ~A então ~B) = (Se A então B) E (Se B então A) = A se e somente se B.
Gabarito letra a)
Tentei explicar de forma simples.
Espero ter ajudado.
Abraço!
-
errei por desatenção.
-
Veja o vídeo que gravei com a resolução dessa questão:
https://youtu.be/Wuy1ADxQ-dU
Professor Ivan Chagas
-
Olhando para a tabela-verdade básica eu vizualizei a resposta. Mas só como esquema de raciocínio, sem pensar do jeito mais fácil, porque estamos treinando...
Enfim, as equivalências se justificam através dos resultados da tabela-verdade.
Para uma condicional ser verdadeira, as duas proposições devem ser verdadeiras ou as duas devem ser falsas.
Na bicondicional também acontece isso: para que o resultado seja verdadeiro as duas proposições têm que ser iguais.
A resposta é a que une as duas condicionais com o conectivo E. Aff... melhor pegar o macete do Prof. Chagas. Muito Bom.
https://www.youtube.com/watch?v=Wuy1ADxQ-dU&feature=youtu.be
-
Alguém pode explicar porque a D está errada?
-
Phoenix Dias, a equivalência da bicondicional p--->q é dada de duas maneiras:
1. (p--->q)^(q--->p)
2. (p--->q)^(~p--->~q) (LETRA A - GABARITO)
No caso da letra D, ela se apresenta assim: (p--->q)^(~q--->~p), o que DIFERE das maneiras expostas mais acima.
Espero ter ajudado. Bons estudos!
-
RESPOSTA A
-----------------------------------------------
O que aprendi com essa questão?
A se e somente se B = (Se A então B) E (Se ~A então ~B) (CERTO) LeandroOliveira
A se e somente se B = (Se A então B) E (Se B então A) (CERTO) LETRA A
A se e somente se B = (Se A então B) E (Se ~B então ~A) (ERRADO) LETRA D
#SEFAZAL
-
Temos no enunciado a bicondicional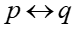 
, onde p = “um número inteiro é par” e q = “o quadrado de um número inteiro é par”.
Sabemos que a bicondicional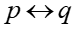 
é formada pela junção de duas condicionais. Ou seja, ela equivale . Escrevendo esta frase, temos:
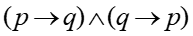se um número inteiro for par, então o seu quadrado é par, e se o quadrado de um número inteiro for par, então o número é par”
Não temos essa opção de resposta, mas temos algo parecido nas alternativas A e D. Para chegar em uma delas, podemos lembrar que q→p é equivalente a ~p→~q, e assim substituir nossa frase por:
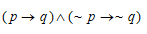
Escrevendo esta última, temos:
se um número inteiro for par, então o seu quadrado é par, e se um número inteiro não for par, então o seu quadrado não é par
Podemos marcar a alternativa A.
Resposta: A
-
Gabarito: letra A.
"um número inteiro é par se e somente se o seu quadrado for par". A equivalência seria:
"Se um número inteiro é par, então o seu quadrado é par E se o quadrado é par, então o número inteiro é par".
Porém, não temos essa alternativa. Sendo assim, devemos, nesse caso, fazer a contrapositiva da segunda condicional pra chegar na resposta. Ficaria assim:
"Se um número inteiro é par, então o seu quadrado é par E se o número inteiro não é par, então o quadrado não é par".
-
Gabarito: A ✔
Sejam as proposições:
p: "Um número inteiro é par."
q: "O quadrado de um número inteiro é par."
A proposição composta pode ser assim representada:
p↔q: "Um número inteiro é par se e somente se o seu quadrado for par."
A bicondicional é equivalente a:
p↔q ≡ (p→q)∧(q→p)
Não temos alternativa que corresponda a essa última equivalência, porém, se realizarmos a contrapositiva de (q→p), encontramos:
p↔q ≡ (p→q)∧ (~p→~q)
Esse resultado pode ser lido como:
(p→q)∧ (~p→~q): "Se um número inteiro for par, então o seu quadrado é par, e se um número inteiro não for par, então o seu quadrado não é par."
Bons estudos!
==============
Materiais: portalp7.com/materiais