-
0,3 corresponde a metade, logo 0,6 corresponde ao total
recipiente vazio = 140 gramas = 0,4
0,2 = 70
70.5 = 350
-
140+C =x (I)
140 + 1/2C = 0,7 (II)
Substitui I em II
140 + 1/2c = 0,7* (140 + c )
c= 210
140 + 210 = 350 - Alternativa A
-
Metade do recipiente: 0,7x
Recipiente vazio: 140g
Recipente cheio: x
0,7+0,7= x - 140
1,4x - x = 140
0,4x = 140
x= 350
-
RE + CON = X
( RE = 140 )
140 + CON = X ...
CON= X - 140 ...
RE + C/2= 0,7X
140 + ( X + 140 ) 7
---------------- = --------- X
2. 10
1400 + 5X + 700 = 7X
7X - 5X = 1400 - 700
2X = 700
X = 700/2
X = 350
-
R + C = x
R = 140g
x = ?
R + C - C/2 = 0,7x
140 + C - C/2 = 0,7x
280 + 2C - C = 1,4x
C = 1,4x - 280
140 + 1,4x - 280 = x
0,4x = 140
x = 350
RESPOSTA: A
-
Seja C a massa do conteúdo
Seja R o recipiente( 140 gramas )
Seja X as gramas
R+C = X
140+C = x
A QUESTAO DIZ '' Se retirarmos exatamente a metade do conteúdo ( C) do recipiente'' ENTAO fica assim:
140+C/2 = 0,7x
140+C/2 = 0,7(140+C)
140+C/2 = 98+0,7C
Passando os ''parzinhos'':
140 - 98 = 0,7 - C/2 (Lembrando que C/2 TEM um ''1'' OCULTO rs entao 1/2 = 0,5) ou seja 0,7 - 0,5 = 0,2
42 = 0,2C
42/0,2 = C
210 = C
LEBRANDO O sisteminha do inicio:
140+C = x
140+210 = 350
gabarito: A
-
Achei esta maneira mais simples de fazer: Seja C a massa do conteúdo - Seja R o recipiente( 140 gramas ) - Seja X as gramas
Equação 1) R+C=X
Equação 2) R +1/2 C=0,7X --> multiplica por 2 --> 2R+C=1,4X
R=140
Coloca-se uma embaixo da outra e subtrai --> (Equação 2 - Equação 1) ---> Fica R=0,4X --> 140=0,4x ---> x=350
-
R + C = X
R + 1/2C = 0,7x(70%)x
R = 40%x 1/2C = 30% C= 60%x
R= 140 = 40%
x = 100%
Regra de 3
x= 350
-
recipiente: 140 g
x = recipiente + conteúdo
x = 140 + c
0,7x = 140 + c/2
0,7 * (140 + c) = 140 + c/2
98 + 0,7c = 140 + c/2
0,7c = 42 + c/2
0,7c - 42 = c/2
2 * (0,7c - 42) = c
1,4c - 84 = c
1,4c - c = 84
0,4c = 84
c = 210
x = 140 + c
x = 140 + 210
x = 350 g
gabarito: A
-
X-0,7x= 0,3x
0,3x+0,3x=0,6x
0,6x+140=x
0,6x-x=-140
-0,4x= -140
X= 140/0,4
X= 350
-
Isso é matemática ...
-
A metade do conteúdo representa 30% de X.
O total do conteúdo representa 60% de X.
140 ------------------- 40%
X ---------------------- 60%
=210
140 + 210 = 350
-
A + B = x
A + B/2b= 0,7x
A= 140
280 + B = 1,4x
(-)140+ B= X
_______________
140= 0,4x
x=350
-
RECIPIENTE + CONTEÚDO = 100%
X C
X - 1/2 = 70% SE METADE DO CONTEÚDO EQUIVALE À 30 %, ENTÃO TODO PESA 60%.
O RECIPIENTE PESA 140g, CORRESPONDENTE AOS 40% RESTANTE.
140g --------------- 40%
X -------------------- 100%
40x = 14000
14000/40 = 350 gramas ( C+R )
-
R+C=X
R+0,5C=0,7X
R=140
__
[140+0,5C=0,7X
[140+C=X
__
C=X-140
140+0,5.(X-140)=0,7X
140+0,5X-70=0,7X
70=0,2X
X=70/0,2
X=350
-
R + C = x (recipiente + conteúdo = x gramas)
R + 0,5C = 0,7x (recipiente + metade do conteúdo = 0,7x gramas)
140 = valor do recipiente
140 + C = x
140 + 0,5C = 0,7x
140 + C = x (-0,5)
140 + 0,5C = 0,7x
--------
-70 -0,5C = -0,5x
140 + 0,5C = 0,7x
subtraio as equações:
--------
70 = 0,2x
x = 70 / 0,2
x = 350
-
Recipiente (r) = 140g
Conteudo (c)
R+C=X (g)
R- C/2=0,7X (g)
Substituindo
140+c=x  (-1) multiplicar
140 -c/2=0,7x
Â
-140-c=-x
140-c/2=0,7x
3c=2(0,6x)
c=1,2x/3
c=0,4x
140g=0,4x
x=140/0,4
x=350
Â
Â
-
Olha, sinceramente, não sei como acertei. Só sei que acertei! Aliás, o último concurso que presto que tem matemática será domingo. Nunca mais!!
Fiz o seguinte,,,
Entendi que 0,7 corresponde a 700.
Dividi por 2.
= 350. Fim!
-
Andréa Camisotti, que a sorte esteja com você domingo, pq foi pura coincidencia essa conta que você fez hahahah
Minha resolução:
R = recipiente
C = conteudo
x = Gramas
Logo , R + C = X (I)
Se retirarmos metade de C , X será 0,7x. Logo => R + 0,5c = 0,7x (II)
Sabendo que R = 140 (III) , basta substituir III e I em II.
140 + 0,5c = 0,7 (140 + c)
C = 210
R + C = X => 140 + 210 = 350 !
-
GABARITO A
R + C = X
R + C/2 = 0,7X
R= 140
Agora só substituição!
140 + C = X
140 + C/2 = 0,7X (agora é fazer conta. Eu preferi multiplicar por 2 pra eliminar a fração. Vai de cada um)
280 + C = 1,4X
C = C
1,4X - 280 = X - 140
X = 350
-
SE RETIRAR METADE DO PESO DO CONTEÚDO DIMINUI EM 30% O VALOR TOTAL DO PESO. LOGO O PESO DO CONTEÚDO CORRESPONDE A 60% DO PESO TOTAL. ENTÃO O VALOR DO RECIPIENTE EQUIVALE A 40%. VAMOS PARA REGRA DE TRÊS:
140 = 40%
X = 100%
X = 140x100
40
x = 350
-
140 g = 40 % ja que quando tiramos metade do conteudo diminuiu 30% do peso
x = 100%
fazer regra 3
x = 350
-
Fiz um raciocínio mais demorado, mas que deu certo (e por sorte no primeiro valor que escolhi testar):
"Qual valor menos 140 (peso do recipiente), dividido por dois (metade do conteúdo) SOMADO ao peso do recipiente (140) equivale a 70% do valor inicial?"
350-140 = 210
210/2 = 105
105+140 = 245
350*0,7 = 245
Gabarito A
-
R.........L/2......L/2
=======......=====
70%T............30%T
interpretação: L/2 é 30% do total, então L representa 60% do total
então: só o R representará 40%T = 140 gramas ----> agora é só ir pela tecnica utilizando as próprias alternativas,ok
-
O resultado era um múltiplo de 7. Eu chutei assim, pois não sei absolutamente nada de matemática. Acho que deu certo!
gab. A
-
https://www.youtube.com/watch?v=5J7N9AUVDzo
-
Após retirar metade do conteúdo, o peso passa a ser 70% do total (0,7x); portanto, metade do conteúdo equivale a 30% do peso, pois 100% - 70% = 30%
Sendo assim, o peso do conteúdo equivale a 60% do total, e o peso do recipiente representa 40% do total.
Colocando na equação, teremos:
0,4x = 140
x = 140/0,4
x = 350
Alternativa A
-
R= recipiente C= conteúdo X= total
R= 140 gramas
R+C= X------> 140 + C = X -----> C = (X-140)
R+C/2 = 0,7X
140 + 0,5X - 70 = 0,7X
70 = 0,2X
350 = X
-
Como a massa do recipiente é 140g, então a massa do conteúdo, no momento inicial, é x – 140, afinal ambos pesam x gramas juntos.
Retirando metade do conteúdo, sobra um conteúdo de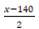 
gramas. Somando com os 140 gramas do recipiente, devemos obter 0,7x gramas, como diz o enunciado. Assim:
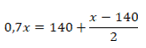
Multiplicando todos os termos por 2, temos:
1,4x = 280 + x – 140
1,4x – x = 140
0,4x = 140
x = 140 / 0,4
x = 350 gramas
Resposta: A
-
-
Macete:
Total = A + B
B = 140
A = 60% do total
então:
B = 40% do total
0,4T = 140 -----> T 350