-
Pelos dados do problema,
30 . k + 40 . y = 1800
k / y = 2 / 3
se
k = preço unitário do panetone de marca K
y = preço unitário do panetone de marca Y
-
Isolando y, obtém-se: y = 30.
Dessa forma, k = 20.
Se fossem comprados 70 panetones da marca Y, teria sido gastos: (70 . 30) reais, isto é, R$ 2100,00, o que corresponde a R$ 300,00 a mais do que a compra feita segundo o enunciado do problema, que foi de R$ 1800,00.
Gabarito: "d"
-
Basta montar 2 equações de 1º grau:
30K + 40Y = 1800
K/Y = 2/3 ========>>>>>>>> K = 2/3(Y)
30 (2/3)(Y) + 40Y = 1800
60Y + 120Y = 5400
Y = 30 (Valor de 1 Panetone)
70 . 30 = 2100 (Valor de 70 Panetones)
Então: 2100 - 1800 = 300
Resposta: Letra D
-
Escrevendo “uma empresa comprou 30 panetones iguais da marca K e 40 panetones iguais da marca Y, pagando um total de R$ 1.800,00”, e “a razão entre os preços unitários dos panetones K e Y é de 2 para 3, nessa ordem”, em linguagem matemática, temos:
30 . K + 40 . Y = 1800
(K / Y) = (2 / 3) → K = (2 . Y) / 3
Substituindo K na primeira equação, temos:
30 . [(2 . Y) / 3) + 40 . Y = 1800
20 . Y + 40 . Y = 1800
60 . Y = 1800
Y = 30 → Y = R$ 30,00
Assim comprando 70 panetones a R$ 30,00 cada, a empresa gastaria um total de:
70 . R$ 30,00 = R$ 2.100,00
Subtraindo R$ 1.800,00 deste valor, obtemos R$ 300,00.
Portanto para comprar somente panetones do tipo Y a empresa tem que investir mais R$ 300,00.
-
30K + 40Y= 1800
K x 2 => 2Y=3K
Y 3
2 Y= 3 K
20 Y= 30K
20Y + 40Y=1800
60Y=1800
Y=30
30 . 7= 2100 => 2100-1800= 300
ALTERNATIVA - D
-
30 panetones k com peso 2 (razão preço unitário 2 para 3 - para cada 2k são 3y)
40 panetones y com peso 3
30 x 2 = 60
40 x 3 = 120
some
60 + 120 = 180
divida
total da compra 1800,00/180 = 10 ( coeficiente de proporcionalidade)
multiplique
60 x 10 = 600 (valor dos 30 panetones k)
120 x 10 = 1200 (valor dos 40 panetones y)
regra de 3
40 y ------------ 1200
70 y ------------ x
x = 1200x70/40 = 2100 (valor caso tivesse comprado os 70 panetones y)
como o valor original da compra era 1800,00 a diferença seria de 300,00
resposta D
-
achei muito simples.
peguei o total 1800/2*=900 depois multipliquei por 3 =2700 depois 2700-1800=900 depois 900/3 ( DIVIDI POR 3 PQ A QUESTAO PEDE A LETRA Y ) =300 R:letra d
obs: toda vez que dividir normalmente tem que multiplicar mais a frente ex: 2 referente a letra k e y referente a letra y como dividi por 2 obrigatoriamente tenho que ficar atento pq terei que dividir mais a frente p/ achar a resposta
-
K/Y= 2/3 multiplicando 2x30=60 e 3x40=120, então 120+60= 180. Já 70x3= 210
180.................1800
210.................. X
X = 2100
2100-1800= 300
-
Cuidado no exercício: não é a razão entre k/y que é 2/3 e sim a razão sobre o preço unitário.
K+Y=70....30+40=70
pk/py = 2/3.......pk=2py/3
30.pk+40.py=1800
30(2py/3)+40.py=1800
60py/3+40.py=1800
60py+120py/3=1800
180py/3=1800
180py=5400
py=5400/180
py=30
30*70=2100
2100-1800=300
alternativa D
-
Montando as equações abaixo de acordo com os dados do enunciado:
30K + 40Y = 1800 (1)
K/Y = 2/3 (2)
Melhorando a equação (2):
K = 2Y/3 (3)
Substituindo a equação (3) em (1):
30(2Y/3) + 40Y = 1800
20Y + 40Y = 1800
60Y = 1800
Y = 30
Logo, se essa empresa tivesse comprado todos os 70 panetones somente da marca Y, ela teria gasto:
70Y = 70(30) = 2100,00
Subtraindo-se esse valor de R$1.800,00:
R$2.100,00 - R$1800,00 = R$300,00
Resposta: Alternativa D.
-
30k+40y=1800
3k-2y=0
Y=30 (resolvendo o sistema)
40x30=1200 reais
40y------1200
70y--------x
x=2100 reais
2100-1800=300 reais
gabarito D
-
30. 2 (razã0) + 40. 3(razão) = 1800
Se for só 70.
0. 2 + 70. 3 = 2100 - (zero x 2 é 0!, portanto chegamos em 2100)
2100 - 1800 = 300
-
30k/2= 15
15.3= 45
15+45= 60
1800/60= 30
70y.30= 2100
2100-1800= 300
Gabarito: D
-
30K +40Y= R$1800,00 K=2X / Y=3X
SUBSTITUINDO
30*2X+40*3X=1800
60X+120X=1800
180X=1800
X=10
ENTÃO
K=2*10=20 / Y=3*10=30 -----------> TODOS OS 70 PANETONES SENDO Y -------> 70*30=2100 --------> 2100-1800=300
-
Preço de K = k
Preço Y = y
30k + 40 y =1.800
e
K 2
Y 3
Fazendo em cruz fica: 3k = 2y
k = 2y / 3
Substituindo a equaçao inicial:
30k + 40 y =1.800
30.(2y) + 40y = 1800
3
60y + 40y = 1800
3
20y+40y = 1800
60y = 1800
y= 30
Se fosse 70 unidades de Y .... 70.30 = 2.100 .... comparando com o valor 1.800... a mais seria 300,00
-
Se a razão é 2/3 , considerei os preços como 20,00 para K e 30,00 para Y. Oras, se são 30 panetones K e 40 panetones Y , temos 20,00 x 30= 600,00 e 30,00 x 40,00 = 1200,00. A questao fala sobre 70 panetones da marca y. Considerando que o valor do panetone y é 30,00 a unidade, teremos 70,00 x 30,00 = 2.100,00 . r$ 2.100-1800,00 =300,00
-
K/Y= 2/3
3K = 2Y
K= 2Y/3
30K + 40Y = 1800
30 *( 2Y/3)+40Y= 1800
60Y/3+ 40Y = 1800
20Y+40Y = 1800
60Y= 1800
Y= 30
SUBSTITUINDO
30K+40Y=1800
30K + 40*(20)= 1800
30K + 1200 = 1800
30K = 1800-1200
30K = 600
K = 20
Se fossem comprados 70 panetones da marca Y, teria sido gastos: (70 *30) = $ 2.100,00
$ 2.100,00 - 1.800,00= $300,00
Alternativa D
-
Vão direto ao comentário do edison, somente com a explicação dele entendi melhor.
-
RESOLUÇÃO:
Chamando de k e y os preços unitários dos panetones das marcas K e Y, respectivamente, temos que o valor total gasto para comprar 30 K e 40 Y é:
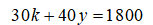
Isolando k, temos:
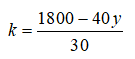
Como a razão entre k e y é de 2 para 3, então:
2 ------------------------ 3
k ------------------------ y
2y = 3k
k = 2y/3
Assim, como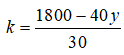
e k = 2y/3, podemos dizer que:
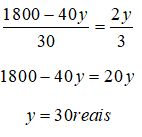
Logo, se tivessem sido comprados 70 panetones da marca Y, o total gasto seria:
70 x 30 = 2100 reais
Assim, o valor gasto a mais seria de 2100 – 1800 = 300 reais.
Resposta: D
-
Em ultima instancia daria pra chutar:
Divide-se 1800 para 5 (haja vista que a razão é 2 para 3)
Resultando em 360
360x2= 720
360x3=1080
SE 1080 reais comprou 40 panetones Y quantos reais vou precisar para comprar quase o dobro (70 panetones)? 1080 com 1080= 2160
2160-1800 (para descobrir a diferença): 360 sabendo que não é o dobro, mas quase o dobro (70): chutaria pra baixo = 300 alternativa D
Se eu estiver errado comentem, pode ter sido mera coincidência; não chutem, estudem. Faça o que eu falo não faça o que eu faço.
-
30K + 40Y = 1800
K/Y = 2/3 ---> K=2/3Y; substituindo K na equação acima fica:
30K + 40Y = 1800
30 . 2Y/3 + 40Y = 1800
60Y/3 + 40Y = 1800
60Y + 120Y = 5400
180Y = 5400
Y=30 reais
70 panetones Y x 30 reais = 2100 reais
2100 - 1800 = 300 reais a mais
-
https://www.youtube.com/watch?v=srJOVZh4LKk (resolução em vídeo)
Gabarito D. Bons estudos! :)