Questões de Sistemas Lineares

ID

136759

Banca

FCC

Órgão

TRF - 4ª REGIÃO

Ano

2010

Provas

FCC - 2010 - TRF - 4ª REGIÃO - Analista Judiciário - Contabilidade

Disciplina

Matemática

Assuntos

Ao conferir a elaboração dos cálculos em um processo, um Analista do Tribunal Regional Federal percebeu que o total apresentado era maior que o valor real. Ele comunicou ao responsável pela elaboração dos cálculos que a diferença encontrada, em reais, era igual ao menor número inteiro que, ao ser dividido por 2, 3, 4, 5 ou 6, resulta sempre no resto 1, enquanto que, quando dividido por 11, resulta no resto 0. Dessa forma, se o valor real era R$ 10 258,00, o total apresentado era

Alternativas

R$ 10 291,00.

R$ 10 345,00.

R$ 10 379,00.

R$ 10 387,00.

R$ 10 413,00.

Comentários

R$ 121,00 é a diferença.Logo o valor encontrado equivocadamente é: 10.258 + 121 = R$ 10.379,00121 é divisível por 2, 3, 4, 5, 6 sempre sobrando resto 1, e também é divisível por 11.
O MMC de 2, 3, 4, 5, 6 é 60. Se o resto é 1, a diferença procurada seria 61. Porém 61 não é divisível por 11. Portanto este resultado não serve.
O próximo MMC de 2, 3, 4, 5, 6 é 120. Somando 1 do resto, temos 121, que é divisível por 11, sendo esta a diferença procurada. Resposta = R$ 10.379,00 Gaba C
Para achar o MMC de 2, 3, 4, 5, 6 devemos fatorar estes números, decompondo-os em fatores primos e eliminando os valores iguais. Portanto o MMC(2,3,4,5,6)= 2*3*(2*2)*5*(2*3)=60.
Bons Estudos!
Caso não se lembre de utilizar o MMC:

Note que apenas as alternativas "a" e "c" apresentam como diferença um número divisível por 11, sendo assim , já seria possível eliminar as alternativas "b", "d" e "e"; Porém, ao dividirmos a diferença encontrada em "a" por 3 obtemos resto zero, portanto sobra a alternativa "c" que preenche o comando da questão confome o gabarito.
"Esforça-te, e tem bom ânimo; não temas, nem te espantes; porque o SENHOR teu Deus é contigo, por onde quer que andares". Js 1.9
a. 10291-10258=33 (33/2=16 r=1) (33/11=3 r=0) (33/3=11 r=0) errado
b. 10345-10258=87 (87/2=43 r=1) (87/11=7 r=1) errado
c. 10379-10258=121 (121/2=60 r=1) (121/11=11 r=0) (121/3=40 r=1) (121/4=30 r=1) (121/5=24 r=1) (121/6=20 r=1) RESPOSTA CERTA
d. 10387-10258=129 (129/2=64 r=1) (129/11=11 r=1) errado
e. 10413-10258=155 (155/2=77 r=1) (155/11=14 r=5) errado
De acordo com o enunciado, verifica-se que o número inteiro procurado deve atender a dois critérios: quando divido por 2, 3, 4, 5 ou 6 ter resto 1 e ser um número divisível por 11.

Assim, deve-se encontrar o mínimo múltiplo comum (MMC) entre 2, 3, 4, 5 e 6 acrescentar uma unidade. Posteriormente verificar se é divisível por 11.

2 3 4 5 6 l 2

1 3 2 5 3 I 2

1 3 1 5 3 I 3

1 1 1 5 1 I 5

1 1 1 1 1

Sendo assim o MMC entre os números é 2 x 2 x 3 x 5 = 60

Somando a unidade: 60 + 1 = 61. O número encontrado atende ao primeiro critério, mas não ao segundo.

Assim, utiliza-se o próximo múltiplo de 2,3,4,5 e 6 que é 120.
Somando a unidade: 120 + 1 = 121. O número encontrado atende aos 2 critérios.

Finalmente, o total apresentado era 10258 + 121 = 10379 reais.

Resposta C.

ID

204526

Banca

CESGRANRIO

Órgão

IBGE

Ano

2010

Provas

CESGRANRIO - 2010 - IBGE - Recenseador

Disciplina

Matemática

Assuntos

No primeiro trimestre do ano passado, o vertedouro (canal de segurança que controla o nível de água) de um lago localizado no Parque da Aclamação, na capital paulista, se rompeu. Em 50 minutos, 780.000 litros de água escoaram, deixando o lago praticamente seco. Em média, quantos litros de água escoaram do lago a cada segundo?

Alternativas

156

180

260

348

Comentários

se 1 minuto tem 60 segundos, logo multiplica-se 50 por 60 que dará 3000
logo é só verificar :
3000 x 156 = 468.000 - ERRADO
3000 x 180 = 540.000 - ERRADO
3000 x 260 = 780.000 - CORRETO
3000 x 348 = 1.844.000 - ERRADO
CORRETA LETRA C
Bons Estudos !!!!
em 1 minuto tem 60 segundos, Logo vamos ter que multiplicar
50 min por 60 segundos q vai dar 3000
agora é só multiplicar 3000 por todas as alternativas para ver o qual vai dar 780.000

Logo, a resposta certa é a letra C
Porque 3000 x 260 é 780.000

Bons Estudos Pessoal !!
Paulo.
Regra de três:
1m ----- 60 s
50 m ---- x
x=3000 s
Agora é so dividir, se 780.000 / 3000 = 260 litros.
780.000 /50 = 15600 l/min.
como 1 min é = a 60s
15600/60 = 260
50 minutos = ( 50 * 60 ) = 3.000 segundos.

780.000 / 3.000 = 260

Resposta: 260 letra c
Primeiro temos que converter 50 minutos para segundo
Sabemos que um minuto = 60 segundos então 50 * 60 = 3000 E A QUESTAO PEDE Em média, quantos litros de água escoaram do lago a cada segundo?
780000/3000= 260
MAS SE FIZERMOS PELO METODO DE REGRA DE TRES SIMPLES FICARIA

SEGUNDOS                  LITROS
     3000       ---------------- 780000
        1         ----------------        X

X= 260 SEGUNDOS
50x60=3000

3 000 = 780 000 ou 3 = 780
1 = x (regra de 3)

780/3 = 260
x=260L/s

Enquanto você multiplica todas as alternativas, seu oponente fez regra de três e já está na próxima questão. Fica a dica.
Primeiro vamos coverter 50 min. em segundos.
50 x 60seg = 3.000 seg.

Aplica-se agora a regra de três.
Segundos. Litros
3000 ---------------- 780000
1 ---------------- X

X= 260 Litros
Eu fiz assim:

Multipliquei 50x60 para saber quantos segundos há em 50 minutos, deu 3000.

Fiz a seguinte regra de três:

3000 ---------- 780000

1 ---------------- x

3000x ---------- 780000

x ------- 260

SUCESSO GALERA!!!
letra C: 260
Eu não usei a regra de 3 e deu o mesmo resultado.
780.000 litros --------------- 50 minutos
X ---------------- 1 minutos
X =78000 litros / 50 min
X = 156000 litros
X = 156000 litros / 60 segundos
X = 260 litros/segundo
turma boa,belezaaaa

ID

243661

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2010

Provas

CESGRANRIO - 2010 - Petrobras - Administrador

Disciplina

Matemática

Assuntos

Sistemas Lineares

Em uma festa comunitária, uma barraca de tiro ao alvo dá um prêmio ao cliente de R$ 30,00, cada vez que o mesmo acerta a área central do alvo. Caso contrário, o cliente paga R$ 10,00. Um indivíduo deu 50 tiros e pagou R$ 100,00. Nessas condições, o número de vezes que ele ERROU o alvo foi

Alternativas

Comentários

Tiros certos: C;
tiros errados: E.
Vamos formar um sistema: E I -> C + E = 50
E II -> 30C - 10E = -100 (é negativo, pq o cliente ficou no prejuizo)
Onde C = 10 e E = 40.
x- Acertos
y-Erros

x+y=50 .(10)

10x+10y=500
30x-10y=-100
---------------------
40x+0=400
x=10, portanto, 10 acertos
y=50-10
y=40, portanto, 40 erros
Ele acertou 10 e errou 40 porque:

erros = 10,00
acertos = 30,00

10 * 30 = 300
40 * 10 = 400
300-400 = -100
100,00 ele ficou devendo

letra E
Solução:
Acertos        (Tiro no alvo) = a;
Erros (Tiros Fora do alvo) = e;

Total de Tiros= a+e, logo, a+e=50;
30a-10e=-100, ou seja, valor dos acertos vezes a quantidade de acertos, menos, valor dos erros vezes a quantidade de erros i gual a -100(já que o atirador teve que pagar).

Sistema:
    a +    e =    50 (x10)   após a multiplicação temos:   10a + 10e = 500
30a - 10e = -100                                                             30a - 10e = -100
                                                                                       _______________

                                                                                        40a = 400

a= 400/40, logo a = 10, substituindo em a +.e = 50, temos, 10 + e = 50, logo, e = 50-10, portanto, e=40.
Quantidade de erros igual a 40.

Sejam “C” o número de tiros certos, “E” o número de tiros errados e “50” o número total de tiros. Consideremos ainda que o cliente recebeu “30C” pelos tiros certos e pagou “10E” pelos tiros errados. Nestas condições, poderemos escrever de acordo com os dados da questão duas equações:

Equação I	C + E = 50	Equação II	30C – 10E = –100
	C = 50 - E		30 x (50 – E) – 10E = –100
			1500 – 30E – 10E = –100
			– 40E = –100 – 1500 X (– 1)
			40E = 1600
			E = 1600/40 = 40 Erros

Total de 50 tiros.
Para cada acerto, ganha $30.
Para cada erro, paga $10.
Ao fim gastou $100.

$100 / $10 = 10 erros.

50 tiros - 10 tiros errados = 40 tiros.

Contabilizando só os 40 tiros, temos que ter o resultado de $0, então:

Para cada 1 acerto (ganho de $30) ele erra 3 vezes (perda de $30).

Dá para perceber facilmente a proporção inversa de 1 para 10, entre quantidades de tiros (1 e 3) e valores ($10 e $30).

Logo, ele errou mais 30 vezes e acertou 10 vezes. Juntando com os 10 erros contabilizados anteriormente, temos 40 erros.
A --> acertos; E --> erros.
- 30.A + (-10.E) = - 100
- A + E = 50 ---> E = 50 - A
30A +(-10.(50-A)) = -100
30A +(-500+10A) = -100
30A -500 + 10A = -100
40A = -100 +500
40A = 400
A = 400/40
A = 10

Se E = 50 - A, fica: E = 50 - 10 --> E = 40
VPNI
cuidado com comentarios errados
1º a pergunta é nº de erros não de acertos

Melhor comentario....CLARO E FACIL
charles freire......muito bom.
obrigada consegui entender .
Seja C o número de vezes que o jogador acertou o alvo, e E o número de vezes que ele errou. Sabemos que ao todo foram 50 jogadas, ou seja:
C + E = 50

Como em cada acerto o jogador ganha 30 reais, o todo ele ganhou 30 x C reais. E, como a cada erro o jogador perde 10 reais, ao todo ele perdeu 10 x E reais. Ao todo, ele pagou 100 reais, ou seja, ficou com um saldo de -100 reais:
30C – 10E = -100

Isolando C na primeira equação, temos que C = 50 – E. Substituindo nesta última, temos:
30 x (50 – E) – 10E = -100
1500 – 30E – 10E = -100
1600 = 40E
E = 40

Logo, ele errou 40 vezes.

Resposta: E

ID

253420

Banca

FCC

Órgão

TRF - 1ª REGIÃO

Ano

2007

Provas

Disciplina

Matemática

Assuntos

Em fevereiro de 2007, Cesário gastou R$ 54,00 na compra de alguns rolos de fita adesiva, todos de um mesmo tipo. No mês seguinte, o preço unitário desse rolo aumentou em R$ 1,50 e, então, dispondo daquela mesma quantia, ele pôde comprar três rolos a menos do que havia comprado no mês anterior. Nessas condições, em março de 2007, o preço unitário de tal tipo de rolo de fita adesiva era

Alternativas

R$ 4,00

R$ 4,50

R$ 5,00

R$ 5,50

R$ 6,00

Comentários

Pelo enunciado do problema, podemos escrever as equações:
1) 54 = q₁.p₁
2) 54 = q₂.p₂
3) p₂ = p₁ +1,5
4) q₂ = q₁ - 3
sendo q₁ a quantidade comprada no primeiro momento e q₂ a comprada no segundo momento; e p₁ o preço do produto no primeiro momento e p₂, no segundo momento.
Trabalhando com as equações e calculando, encontra-se:
54 = (p₁ + 1,5)(q₁ - 3)
-3p₁ + 1,5q₁ = 4,5
Usando a equação (1), chega-se a:
p1^{2 +}1,5p₁- 27 = 0
p₁ = 4,5 ou p₁ = -6 (descarta-se essa solução negativa)
-
Pela equação (3), p₂ = 6.
Gabarito: E
Primeiramente eu convencionei que "X" = quantidade comprada e que "Y" = valor unitário

o item afirma o seguinte
1) 54 = X.Y
2) 54 = (X-3).(Y+1,5)

a partir desse ponto devemos escolher uma variável para isolar ( eu vou isolar o "X")
1) 54 = X.Y
    54/Y = X
    X = 54/Y

agora irei substituir o valor encontrado na equação "2"
2) 54 = (X-3).(Y+1,5)
     54 = (54/Y).(Y+1,5)
     o resultado dessa conta será:
     -3Y2-4,5Y+81 = 0   (dividi por -3)
     Y2+1,5Y-27=0

Equação de 2° grau
Delta = 10,5

Ao resolver a equação acharemos os valores :
Y1 = 6
Y2 = -4,5 (esse valor é despresado)

Logo se "Y" era o valor unitário do produto e este é igual a r$ 6,00 gabarito letra "E"
Galera, só uma dúvida:

Tipo, quando vocês falaram que o resultado é "E" (6), se pegarmos o enunciado da questão, ele fala que "dispondo daquela mesma quantia, ele pôde comprar três rolos a menos do que havia comprado no mês anterior". Se você pegar o número 6, ele poderá comprar 9 rolos, correto?
Agora, quando cada rolo aumentar 1.50, ele só poderá comprar 7 e não três a menos como o enunciado da questão fala.

Todavia, quando se pega a letra "B", relata-se que ele comprará 12 unidades, se cada uma custar 4.50 e com o aumento de 1.50, ele comprarar 9 unidades, logo, as três unidades a menos que o enunciado fala!

Alguém pode me explicar?

Agradeço a compreenssão e bons estudos a todos.
Vagner, o enunciado pede o preço do rolo em março, logo, R$ 6 já é o valor após o aumento do preço:
Fev/2007: 12 rolos X R$ 4,50 = R$ 54
Mar/2007: 9 rolos X R$ 6,00 = R$ 54 (R$ 1,5 a mais no preço, 3 rolos a menos)
Marcelo Rauber, valeu, eu que interpretei a questão de outra maneira.....
Meu raciocínio estava correto, porém, por falta de atenção, respondi a questão de maneira errada.
Valeu e bons estudos.
Mês de fevereiro/2007:
Preço unitário = x
Quantidade de rolos = y
Total gasto = 54
Equação>> x.y = 54

Mês de março/2007
Preço unitário = x + 1,5
Quantidade de rolos = y - 3
Total gasto = 54
Equação>> (x + 1,5).(y - 3) = 54

Eliminando os parênteses: x.y - 3x + 1,5y - 4,5 = 54
Substituindo x.y por 54, fica assim:
54 - 3x + 1,5y - 4,5 = 54
1,5y - 3x - 4,5 = 54 - 54
1,5y - 3x - 4,5 = 0
Substituindo y, fica assim:
1,5 (54/x) - 3x - 4,5 = 0
Resulta na equação do 2º grau:
3x2 + 4,5x - 81 = 0
Resolvendo a equação, encontrará x = 4,5 (preço unitário em fevereiro)
Preço unitário em março = 4,50 + 1,50 = R$ 6,00

Vamos conferir? Quantos rolos posso comprar com R$ 54,00, se cada rolo custa R$ 4,50 ?
54 / 4,5 = 12 rolos

E quantos poderei comprar se o preço unitário aumentar em R$ 1,50, isto é, passar a custar R$ 6,00 ?
54 / 6 = 9 (posso comprar 3 rolos a menos)
Vamos responder usando as alternativas.
a) 54/4=13,5 – Não dá resultado exato
b) 54/4,5=12 , 4,5-1,5=3 , 54/3=18 (diferença de 5 unidades)
c) 54/5=10,8 – Não dá resultado exato
d) 54/5,5=9,81 – Não dá resultado exato
e) 54/6=9 ,6-1,5=4,5 , 54/4,5=12 , 12-9=3 (diferença de 3 unidades)
Nesse tipo de questão é importante ter em mente que o TEMPO e a PRESSÃO psicológica no momento da prova são muito grandes.

Desta forma, equacionar o problema até resolvê-lo pode levar muito tempo e comprometer a resolução de outras questões.

Na hora de resolver questões de matemática em uma prova objetiva, o mais importante é encontrar o CAMINHO MAIS CURTO para se chegar à resposta.

Conforme pude observar nos comentários anteriores, o método mais prático e rápido para resolver o problema foi o de Luanna Carize Padilha Macedo.
Mês de fevereiro/2007:
Preço unitário = x
Quantidade de rolos = y
Total gasto = 54
Equação>> x.y = 54

Mês de março/2007
Preço unitário = x + 1,5
Quantidade de rolos = y - 3
Total gasto = 54
Equação>> (x + 1,5).(y - 3) = 54

Eliminando os parênteses: x.y - 3x + 1,5y - 4,5 = 54
Substituindo x.y por 54, fica assim:
54 - 3x + 1,5y - 4,5 = 54
1,5y - 3x - 4,5 = 54 - 54
1,5y - 3x - 4,5 = 0
Substituindo y, fica assim:
1,5 (54/x) - 3x - 4,5 = 0
Resulta na equação do 2º grau:
3x2 + 4,5x - 81 = 0
Resolvendo a equação, encontrará x = 4,5 (preço unitário em fevereiro)
Preço unitário em março = 4,50 + 1,50 = R$ 6,00
Como preço unitário, temos: mês de fevereiro :X , mês de março : X . 1,50. Já a quantidades de rolos comprados, no mês de fevereiro,

compramos Y, em março : Y - 3. O dinheiro gasto nos dois meses foram os mesmos : R$ 54,00

Montando o sistema, temos:

X . Y =54 (1° equação)
(X . 1,50) . (Y - 3) = 54 ( 2° equação)

Resolvendo-o:

Aplicando a propriedade distributiva na segunda equação, temos:

(X . 1,50) . (Y - 3) = 54

1,50 X .Y - 4,50X = 54

Substituindo, o X . Y da primeira equação na segunda:

1,50 . 54 - 4,5 X = 54

81 - 4,5 X = 54

-4,5 X = 54 - 81 . (-1)

4,5 X = 81 - 54

X = 27 / 4,5

X = 6.

Resposta: letra E
A Quantidade de rolos comprada (x) e o seu Preço unitário (Y) são grandezas inversamente proporcionais e assim:

N° Rolos     Preço unitário
    x                         y
   x-3                     y+1,50

Então: x.y = (x-3) . (Y+1,50)

Sabendo que x.y = 54, temos:

54 = (x-3) . (Y+1,50)

Se  x.y = 54, podemos isolar o x, x= 54/y

Substituindo o x na equação 54 = (x-3) . (Y+1,50)

Chegamos em: -3y² -4,5y + 81=0

Que resulta em duas raízes, 12 e -9.

Desconsiderando a raiz negativa,

Se x= 12 e (x-3) é a qtde de rolos comprados em março, temos que foram comprados 9 rolos ( 12-3) e assim 54 (Preço total) / 09 = R$6,00
Tb fiz igual a Luana, respondi me baseando pelas alternativas.... mas se engana quem pensa que leva menos tempo... vc tem que fazer todas as continhas ali na hora... mas para mim foi o único modo de acertar a questão... resta saber se na prova teria conseguido tempo para responder...

Na verdade eu pegava as alternativas e multiplicava por um número que chegasse perto de 54... se desse certo ainda tinha que verificar se com R$ 1,50 a menos aumentava 3 casas (o valor das alternativas era para o mês do aumento, então no mês anterior você tinha que diminuir R$ 1,50 e multiplicar por um número maior do que o usado anteriormente, já que em fevereiro ele comprou 3 a mais)...

mas como a resposta estava na última alternativa... você faz muitas contas e perde um tempinho...
Como são rolos, só valem números inteiros:

a) 54 : 4 = 13,5

b) 54 : 4,5 = 12 (número inteiro)

c) 54 : 5 = 10,8

d) 54 : 5,5 = 9,2

e) 54 : 6 = 9 (número inteiro)

b) 54 : 4,5 = 12

4,5 - 1,5 = 3

54 : 3 = 18

18 - 12 = 6 rolos

e) 54 : 6 = 9

6 - 1,5 = 4,5

54 : 4,5 = 12

12 - 9 = 3 rolos

ID

256462

Banca

VUNESP

Órgão

TJ-SP

Ano

2011

Provas

VUNESP - 2011 - TJ-SP - Escrevente Técnico Judiciário

Disciplina

Matemática

Assuntos

Uma empresa comprou 30 panetones iguais da marca K e 40 panetones iguais da marca Y, pagando um total de R$ 1.800,00. Sabendo-se que a razão entre os preços unitários dos panetones K e Y é de 2 para 3, nessa ordem, pode-se afirmar que se essa empresa tivesse comprado todos os 70 panetones somente da marca Y, ela teria gasto, a mais,

Alternativas

R$ 600,00.

R$ 500,00.

R$ 400,00.

R$ 300,00.

R$ 200,00.

Comentários

Pelos dados do problema,
30 . k + 40 . y = 1800
k / y = 2 / 3
se
k = preço unitário do panetone de marca K
y = preço unitário do panetone de marca Y
-
Isolando y, obtém-se: y = 30.
Dessa forma, k = 20.
Se fossem comprados 70 panetones da marca Y, teria sido gastos: (70 . 30) reais, isto é, R$ 2100,00, o que corresponde a R$ 300,00 a mais do que a compra feita segundo o enunciado do problema, que foi de R$ 1800,00.

Gabarito: "d"
Basta montar 2 equações de 1º grau:

30K + 40Y = 1800
K/Y = 2/3 ========>>>>>>>> K = 2/3(Y)

30 (2/3)(Y) + 40Y = 1800
60Y + 120Y = 5400
Y = 30 (Valor de 1 Panetone)

70 . 30 = 2100 (Valor de 70 Panetones)

Então: 2100 - 1800 = 300

Resposta: Letra D
Escrevendo “uma empresa comprou 30 panetones iguais da marca K e 40 panetones iguais da marca Y, pagando um total de R$ 1.800,00”, e “a razão entre os preços unitários dos panetones K e Y é de 2 para 3, nessa ordem”, em linguagem matemática, temos:

30 . K + 40 . Y = 1800

(K / Y) = (2 / 3) → K = (2 . Y) / 3

Substituindo K na primeira equação, temos:

30 . [(2 . Y) / 3) + 40 . Y = 1800

20 . Y + 40 . Y = 1800

60 . Y = 1800

Y = 30 → Y = R$ 30,00

Assim comprando 70 panetones a R$ 30,00 cada, a empresa gastaria um total de:

70 . R$ 30,00 = R$ 2.100,00

Subtraindo R$ 1.800,00 deste valor, obtemos R$ 300,00.

Portanto para comprar somente panetones do tipo Y a empresa tem que investir mais R$ 300,00.
30K + 40Y= 1800

K x 2 => 2Y=3K
Y 3

2 Y=   3 K
20 Y= 30K

20Y + 40Y=1800
           60Y=1800
               Y=30

30 . 7= 2100 =>    2100-1800= 300

ALTERNATIVA - D
30 panetones k com peso 2 (razão preço unitário 2 para 3 - para cada 2k são 3y)
40 panetones y com peso 3
30 x 2 = 60
40 x 3 = 120
some
60 + 120 = 180
divida
total da compra 1800,00/180 = 10 ( coeficiente de proporcionalidade)

multiplique
60 x 10 = 600 (valor dos 30 panetones k)
120 x 10 = 1200 (valor dos 40 panetones y)
regra de 3
40 y ------------ 1200
70 y ------------ x
x = 1200x70/40 = 2100 (valor caso tivesse comprado os 70 panetones y)
como o valor original da compra era 1800,00 a diferença seria de 300,00
resposta D
achei muito simples.
peguei o total 1800/2*=900 depois multipliquei por 3 =2700 depois 2700-1800=900 depois 900/3 ( DIVIDI POR 3 PQ A QUESTAO PEDE A LETRA Y ) =300 R:letra d

obs: toda vez que dividir normalmente tem que multiplicar mais a frente ex: 2 referente a letra k e y referente a letra y como dividi por 2 obrigatoriamente tenho que ficar atento pq terei que dividir mais a frente p/ achar a resposta
K/Y= 2/3 multiplicando 2x30=60 e 3x40=120, então 120+60= 180. Já 70x3= 210

180.................1800
210.................. X

X = 2100

2100-1800= 300
Cuidado no exercício: não é a razão entre k/y que é 2/3 e sim a razão sobre o preço unitário.

K+Y=70....30+40=70
pk/py = 2/3.......pk=2py/3

30.pk+40.py=1800
30(2py/3)+40.py=1800
60py/3+40.py=1800
60py+120py/3=1800
180py/3=1800
180py=5400
py=5400/180
py=30

30*70=2100
2100-1800=300
alternativa D
Montando as equações abaixo de acordo com os dados do enunciado:

30K + 40Y = 1800 (1)
K/Y = 2/3 (2)

Melhorando a equação (2):

K = 2Y/3 (3)

Substituindo a equação (3) em (1):

30(2Y/3) + 40Y = 1800
20Y + 40Y = 1800
60Y = 1800
Y = 30

Logo, se essa empresa tivesse comprado todos os 70 panetones somente da marca Y, ela teria gasto:

70Y = 70(30) = 2100,00

Subtraindo-se esse valor de R$1.800,00:

R$2.100,00 - R$1800,00 = R$300,00

Resposta: Alternativa D.
30k+40y=1800

3k-2y=0

Y=30 (resolvendo o sistema)

40x30=1200 reais

40y------1200

70y--------x

x=2100 reais

2100-1800=300 reais

gabarito D
30. 2 (razã0) + 40. 3(razão) = 1800

Se for só 70.

0. 2 + 70. 3 = 2100 - (zero x 2 é 0!, portanto chegamos em 2100)

2100 - 1800 = 300
30k/2= 15
15.3= 45
15+45= 60
1800/60= 30
70y.30= 2100
2100-1800= 300

Gabarito: D
30K +40Y= R$1800,00 K=2X / Y=3X

SUBSTITUINDO

30*2X+40*3X=1800

60X+120X=1800

180X=1800

X=10

ENTÃO

K=2*10=20 / Y=3*10=30 -----------> TODOS OS 70 PANETONES SENDO Y -------> 70*30=2100 --------> 2100-1800=300
Preço de K = k

Preço Y = y

30k + 40 y =1.800

e

K 2

Y 3

Fazendo em cruz fica: 3k = 2y

k = 2y / 3

Substituindo a equaçao inicial:

30k + 40 y =1.800

30.(2y) + 40y = 1800

3

60y + 40y = 1800

3

20y+40y = 1800

60y = 1800

y= 30

Se fosse 70 unidades de Y .... 70.30 = 2.100 .... comparando com o valor 1.800... a mais seria 300,00
Se a razão é 2/3 , considerei os preços como 20,00 para K e 30,00 para Y. Oras, se são 30 panetones K e 40 panetones Y , temos 20,00 x 30= 600,00 e 30,00 x 40,00 = 1200,00. A questao fala sobre 70 panetones da marca y. Considerando que o valor do panetone y é 30,00 a unidade, teremos 70,00 x 30,00 = 2.100,00 . r$ 2.100-1800,00 =300,00
K/Y= 2/3

3K = 2Y

K= 2Y/3

30K + 40Y = 1800

30 *( 2Y/3)+40Y= 1800

60Y/3+ 40Y = 1800

20Y+40Y = 1800

60Y= 1800

Y= 30

SUBSTITUINDO

30K+40Y=1800

30K + 40*(20)= 1800

30K + 1200 = 1800

30K = 1800-1200

30K = 600

K = 20

Se fossem comprados 70 panetones da marca Y, teria sido gastos: (70 *30) = $ 2.100,00

$ 2.100,00 - 1.800,00= $300,00

Alternativa D
Vão direto ao comentário do edison, somente com a explicação dele entendi melhor.
RESOLUÇÃO:
Chamando de k e y os preços unitários dos panetones das marcas K e Y, respectivamente, temos que o valor total gasto para comprar 30 K e 40 Y é:

Isolando k, temos:

Como a razão entre k e y é de 2 para 3, então:
2 ------------------------ 3
k ------------------------ y
2y = 3k
k = 2y/3

Assim, como e k = 2y/3, podemos dizer que:

Logo, se tivessem sido comprados 70 panetones da marca Y, o total gasto seria:
70 x 30 = 2100 reais

Assim, o valor gasto a mais seria de 2100 – 1800 = 300 reais.
Resposta: D
Em ultima instancia daria pra chutar:

Divide-se 1800 para 5 (haja vista que a razão é 2 para 3)

Resultando em 360

360x2= 720
360x3=1080

SE 1080 reais comprou 40 panetones Y quantos reais vou precisar para comprar quase o dobro (70 panetones)? 1080 com 1080= 2160

2160-1800 (para descobrir a diferença): 360 sabendo que não é o dobro, mas quase o dobro (70): chutaria pra baixo = 300 alternativa D

Se eu estiver errado comentem, pode ter sido mera coincidência; não chutem, estudem. Faça o que eu falo não faça o que eu faço.
30K + 40Y = 1800
K/Y = 2/3 ---> K=2/3Y; substituindo K na equação acima fica:

30K + 40Y = 1800
30 . 2Y/3 + 40Y = 1800
60Y/3 + 40Y = 1800
60Y + 120Y = 5400
180Y = 5400
Y=30 reais

70 panetones Y x 30 reais = 2100 reais

2100 - 1800 = 300 reais a mais
https://www.youtube.com/watch?v=srJOVZh4LKk (resolução em vídeo)

Gabarito D. Bons estudos! :)

ID

260143

Banca

FCC

Órgão

TRT - 4ª REGIÃO (RS)

Ano

2011

Provas

FCC - 2011 - TRT - 4ª REGIÃO (RS) - Analista Judiciário - Tecnologia da Informação

Disciplina

Matemática

Assuntos

Ultimamente tem havido muito interesse no aprovei- tamento da energia solar para suprir outras fontes de energia. Isso fez com que, após uma reforma, parte do teto de um salão de uma empresa fosse substituída por uma superfície retangular totalmente revestida por células solares, todas feitas de um mesmo material. Considere que:

- células solares podem converter a energia solar em energia elétrica e que para cada centímetro quadrado de célula solar que recebe diretamente a luz do sol é gerada 0,01 watt de potência elétrica;

– a superfície revestida pelas células solares tem 3,5 m de largura por 8,4 m de comprimento.

Assim sendo, se a luz do sol incidir diretamente sobre tais células, a potência elétrica que elas serão capazes de gerar em conjunto, em watts, é:

Alternativas

294 000.

38 200.

29 400.

3 820.

2 940.

Comentários

1º passo-
calcular a área da superfície retangular.
Área do retângulo é igual a medida da base x a medida da altura. (A = b.h)
base= 8,4 m
altura= 3,5m.
Logo 8,4 x 3,5 = 29,40m²
2º passo-
agora dividimos o resultado por 0,01w
29,40/0,01= 2940w
1º) Calcula-se a área do retângulo:

Área = Largura x Comprimento
Área = 3,5 x 8,4
Área = 29,4 m²

2°) Converte-se a área de m² para cm²:

A = 29,4 m² = 294000 cm²

3º) Usa-se uma regra de três simples:

1 cm² = 0,01w
294000 cm² = X

X = 2940w

Resposta: E
Pelos dados fornecidos no enunciado é possível calcular a área do retângulo (largura x comprimento), assim:

8,4 m = 840cm

3,5 m = 350cm

área = 840cm x 350cm = 294000 cm²

Como, para cada centímetro quadrado de célula solar que recebe diretamente a luz do sol é gerada 0,01 watt de potência elétrica, em 294000 cm², tem-se:

1 cm² ------------- 0,01 watt

294000 cm² -------------- N watts

N = 2940 w

(Resposta E)

ID

285466

Banca

FGV

Órgão

CODESP-SP

Ano

2010

Provas

FGV - 2010 - CODESP-SP - Técnico - Serviços Portuários - Administrativo - Tipo 1

Disciplina

Matemática

Assuntos

No depósito do porto, esperando para embarque, há diversas pilhas de tábuas, todas com 1,30m de altura, e cada pilha possui tábuas de 2cm e de 3cm de espessura. Se certa pilha contém ao todo 53 tábuas, o número de tábuas de 2cm dessa pilha é

Alternativas

27.

25.

29.

33.

31.

Comentários

Letra C.

Vamos chamar de D, as tábuas de 2cm e de T as de 3cm

D+T = 53
2D+3T = 1,3m = 130 cm

D = 53 - T

2(53-T) + 3T =130
106 -2T + 3T =130
106 + T = 130
T = 130-106
T = 24

D = 53-24
D = 29
não entendi e desisto de entender
Galera,vou tentar explicar meu raciocínio:

2x+3y=130_[Coloquei tudo em centímetros]
x+y=53

Após montar o esquema, multipliquei a parte de baixo por -2,ficando:

2x+3y=130
-2x-2y=-106

Após os cálculos,x=29 e y=24

Espero ter ajudado.

ID

337867

Banca

CS-UFG

Órgão

UFG

Ano

2010

Provas

Disciplina

Matemática

Assuntos

As idades dos pais de Joana somam 62 e a quinta parte da idade de seu pai mais a terça parte da idade de sua mãe é 16. Sabendo que a mãe de Joana tem o triplo de sua idade, qual é a idade de Joana?

Alternativas

Comentários

Alguem por favor poderia postar a resolução desta questão?

Agradeço!
X=idade do pai

Y=idade da mãe

X+Y=62

X/5+Y/3=16

Então resolvendo o sistema temos que a idade da mãe e 27 e a idade do pai e 35 logo a idade da filha e 9 anos.
Pai de Joana: P
Mãe de Joana: M
Joana: J

"As idades dos pais de Joana somam 62": P + M = 62 {1ª equação}
"[...] a quinta parte da idade de seu pai mais a terça parte da idade de sua mãe é 16": P/5 + M/3 = 16 {2ª equação}
"[...] a mãe de Joana tem o triplo de sua idade": M = 3J {3ª equação}

____________________________________________________________________________________________________________________

-> Isole a variável "P" da 1ª equação, substitua na 2ª equação e ache o valor de "M". Após isso, basta pegar o valor de "M" e substituir na 3ª equação. Vamos lá!

P + M = 62
P = 62 - M

P/5 + M/3 = 16
(62 - M)/5 + M/3 = 16 {Ache o MMC entre 5 e 3 (que é 15). Depois, aplique a propriedade de somar duas frações}
(186 - 3M + 5M)/15 = 16 {multiplique cruzado o 15 pelo 16}
186 - 3M + 5M = 240
2M = 240 - 186
2M = 54
M = 54 / 2
M = 27

-> Já temos a idade da mãe de Joana (27). Agora basta jogar na 3ª equação para encontrar a idade de Joana.

M = 3J
27 = 3J
J = 27 / 3
J = 9

GABARITO: D

ID

346732

Banca

CESPE / CEBRASPE

Órgão

PM-ES

Ano

2010

Provas

CESPE - 2010 - PM-ES - Soldado da Polícia Militar

Disciplina

Matemática

Assuntos

Considerando que a soma das idades de 2 meninos seja igual a
8 anos, que essas idades, em anos, sejam medidas por números
inteiros e que cada menino tenha pelo menos 2 anos de idade,
julgue os itens a seguir.

Se a diferença entre as idades dos meninos for 2 anos, então o produto das medidas dessas idades, em anos, será inferior a 14.

Alternativas

Certo

Errado

Comentários

INTERPRETANDO A QUESTÃO:

1º Considerando que a soma das idades de 2 meninos seja igual a 8 anos      x + y = 8

2º que essas idades, em anos, sejam medidas por números
inteiros e que cada menino tenha pelo menos 2 anos de idade   x> ou =2 y> ou =2

3º Se a diferença entre as idades dos meninos for 2 anos   x - y = 2

4º então o produto das medidas dessas idades, em anos, será inferior a 14. x . y = 14 ?

RESOLUÇÃO:

Quais números que somados darão 8 ?  Poderão ser: 4+4=8, 1+7=8, 3+5=8, etc...

Que sejam maiores ou iguais que 2 ?    Poderão ser apenas: 4+4=8, 3+5=8 2+6=8

Que sua diferença de idade seja 2 ? Poderá ser apenas: 3+5=8

UM TERÁ 3 ANOS E O OUTRO 5.

O produto das medidas dessas idades, em anos, será inferior a 14 ? 3.5 =15 QUESTÃO (ERRADA)

RUMO A PM-AL
Gabarito ERRADO

1º Considerando que a soma das idades de 2 meninos seja igual a 8 anos = x + y = 8 (anos)

2º Se a diferença entre as idades dos meninos for 2 anos = x - y = 2 (anos)

x + y = 8 5 + y = 8

x - y = 2 y = 8 - 5

2x = 10 (Fazendo-se a soma em linha) y = 3 (Encontramos o y)

x = 10/2

x = 5 (Encontramos o x)

Então o produto das medidas dessas idades, em anos = 5 X 3 será igual a 15, ou seja, superior a 14.

ID

346735

Banca

CESPE / CEBRASPE

Órgão

PM-ES

Ano

2010

Provas

CESPE - 2010 - PM-ES - Soldado da Polícia Militar

Disciplina

Matemática

Assuntos

Se a diferença entre as idades dos meninos for maior que 3 anos, então um dos meninos terá idade superior a 5 anos.

Alternativas

Certo

Errado

Comentários

x-y= >3 anos

6-2=4 (a questão diz que as crianças devem ter pelo menos 2 anos cada)

logo, para que a diferença entre as idades seja > 3 anos um dos dois terá idade superior a 5 anos.
Gabarito CERTO

1º Considerando que a soma das idades de 2 meninos seja igual a 8 anos = x + y = 8 (anos)

2º Se a diferença entre as idades dos meninos for maior que 3 anos = x - y = >3 (anos)

x + y = 8 6 + y = 8

x - y = 4 (Suponhamos que seja 4) y = 8 - 6

2x = 12 (Fazendo-se a soma em linha) y = 2 (Encontramos o y)

x = 12/2

x = 6 (Encontramos o x)

Então um dos meninos terá idade superior a 5 anos. Pois um terá 6 e outro terá 2 anos.

ID

348934

Banca

FUNDEP (Gestão de Concursos)

Órgão

CODIUB

Ano

2010

Provas

FUNDEP (Gestão de Concursos) - 2010 - CODIUB - Programador de Computador - Júnior

Disciplina

Matemática

Assuntos

Considere dois números positivos tais que

- a soma deles é igual a 45;
- o maior deles é igual ao quadrado do outro menos 11.

Analise as seguintes afirmativas a respeito dos dois números citados e assinale com V as verdadeiras e com F as falsas.

(_) O menor número é um múltiplo do maior.
(_) A multiplicação desses dois números é maior que 250.
(_) O menor dos números vale 8.
(_) O maior número subtraído do menor vale 31.

Assinale a alternativa que apresenta a sequência de letras CORRETA.

Alternativas

(F) (V) (F) (V)

(V) (F) (V) (V)

(V) (F) (V) (F)

(F) (V) (F) (F)

Comentários

O maior vale 38 e o menor vale 7 portando a resposta deveria ser F.V.F.V mas dru como errado pq?
O maior número subtraído do menor vale -31.

''eu acho'' que ele está falando (7-38) e não menor número subtraído do maior, como é feita a subtração!
X + Y = 45

X = Y² - 11
Y² + Y -11 - 45 = 0
Y² + Y - 56 = 0

Aplica fórmula de bhaskara!

y' = 7 (menor)

x + 7 = 45

x = 38
na verdade, eu achei quatro pares de números
A opção correta é A mesmo. Eu procurei a prova e o gabarito oficial.
Ambos se encontram nesses links.
PROVA: https://arquivo.pciconcursos.com.br/provas/14522096/18801ce9aad2/204_programador_computador_junior.pdf
GABARITO:http://www.codiub.com.br/codiub/acervo/concurso/gabaritos.pdf

ID

354940

Banca

FADESP

Órgão

Prefeitura de Juruti - PA

Ano

2010

Provas

FADESP - 2010 - Prefeitura de Juruti - PA - Assistente Administrativo

Disciplina

Matemática

Assuntos

No Festival das Tribos, serão vendidos 8000 ingressos para as arquibancadas e cadeiras do Tribódromo. Os ingressos das arquibancadas custarão R$ 5,00 cada e os das cadeiras R$ 100,00. Se todos os ingressos forem vendidos, a arrecadação será de R$ 87.500,00. Quantas cadeiras serão postas à venda?

Alternativas

7500.

750.

600.

500.

Comentários

QUANTIDADE DE INGRESSOS = 8.000

ARQUIBANCADAS = R$ 5,0

CADEIRAS = R$ 100,00

5 * X + 100 * Y = 87.500

X + Y = 8.000

X = 8.000 - Y

5 * (8.000 -Y ) + 100 * Y = 87.500

40.000 - 5 Y + 100 Y = 87.500

- 5 Y + 100 Y = 87.500 - 40.000

95 Y = 47.500

Y = 47.500 / 95

Y = 500 CADEIRAS

ID

361357

Banca

VUNESP

Órgão

FUNDAÇÃO CASA

Ano

2010

Provas

Disciplina

Matemática

Assuntos

Em um jogo de basquete, um dos times, muito mais forte, fez 62 pontos a mais que o seu adversário, que fez apenas a terça parte do total de pontos feitos pelo time vencedor. Nesse jogo, o time derrotado marcou

Alternativas

21 pontos.

31 pontos.

32 pontos.

42 pontos.

48 pontos.

Comentários

Time vencedor fez x pontos.
Time derrotado fez (x/3) pontos.

x - (x/3) = 62
(3x/3) - (x/3) = (186/3)
3x - x = 186
2x = 186
x = 186/2
x = 93

Time derrotado fez (x/3) = 93/3 = 31 pontos

Resposta: (B) 31 pontos.

Fonte: http://br.answers.yahoo.com/question/index?qid=20100308074539AAoQbJc
Olá
Gabarito B

Outro jeito de se fazer

A = vencedor
B = perdedor

A = 62 + B
B = A/3

A = 62 + B
A = 62 + A/3
3A = 186 + A
2A = 186
A = 93

B = A/3
B = 93/3
B = 31
supondo que esses times, sejam os times A e B, e que o time A fez x pontos, então o time B fez x+62. Como o time perdedor fez apenas a terça parte do total de pontos que o vencedor, e o time vencedor fez x+62 pontos, isso implica dizer q x = (x+62)/3 , sendo assim: 3x = x+62 ; 2x =62 ; x = 62/2 ; x = 31.

Resposta : letra B
Vejamos,

1° - "Em um jogo de basquete, um dos times, muito mais forte, fez 62 pontos a mais que o seu adversário..." Vamos chamar de TIME X, o time vencedor.
2° - "...que fez apenas a terça parte do total de pontos feitos pelo time vencedor." E chamar o TIME Y, o time perdedor.

Se o TIME X fez 62 pontos a mais do que o TIME Y, então temos: x = 62 + y.
Se o TIME Y fez a terça parte do total de pontos do TIME X, então temos: y = 1/3 * x *(o x aqui não se refere ao time x em si, mas ao total de pontos do time x que ainda não sabemos).

Vale lembrar o seguinte: quando no problema aparece as preposições de, da, do, por exemplo, significa que a operação ultilizada é a MULTIPLICAÇÃO!

Agora é somente resolver as questões... -> x = 62 + y // y = 1/3 * x -> x/3

TIME X
x = 62 + y (reparem no valor de y que é = x/3)
x = 62 + x/3
x = 186 + x/3 -> o 3 vai multiplicando para o outro lado.
3x = 186 + x
2x = 186
x = 93 -> O time vencedor marcou um total de 93 pontos. Para descobrir o total de pontos do time y fica possível, já que sabemos o valor de x.

TIME Y
y = x/3
y = 93/3
y = 31 -> O time perdedor marcou um total de 31 pontos.

Alternativa B
Olá pessoal.
Que bom que o pessoal aqui resolve tudo mas na hora da prova, tempo é precioso...
Se chamamos o time vencedor de V e perdedor P, os comentários acima já provaram que podemos montar o sistema de equações:
V - P = 62 (1)
V/P = 3 (2)
Só que na hora da prova, só é interessante achar V se quisermos conferir a resposta. Acho que vale a pena procurar quanto foi o time vencedor se depois de resolver tudo, quiser conferir o resultado. Vá direto achar o valor de P e pronto, vai pra próxima questão.
Não quero desmerecer o que os colegas estão resolvendo, apenas dando uma dica pros concurseiros aqui!

Opa, o resultado....
Pegando a equação (2), temos V = 3P, e substituímos em (1), fica
3P - P = 62
2P = 62
P = 31
Como falei, se tiver tempo sobrando, substitua então novamente nas duas equações e confira o resultado...
Resposta: letra B
Só a alternativa B você pode multiplicar por 3 (31x3 = 93), dividir por 3 (93: 3= 31) e a diferença encontrada (93 - 31) ser igual 'a diferença citada na alternativa : 62 . Sem perder tempo com muitas equações..
Modo mais fácil de resolver:
Time A (vencedor) e Time B (Derrotado).

1) A=B+62 (O time a fez 62 pontos a mais do que o time B)
2) B=A/3 (O time B fez um terço dos pontos do time A)

com a equação B=A/3 ==> A=3B

junte as duas equações: 3B = 3B+62 ==> 2B=62 ==> B=31.
:D
um jeito mais simples para resolver pode ser usando regra de tres simples.

se o time "A" (vencedor) pontuou 62 pontos a mais que o time "B" (perdedor) e no enunciado diz que o time B fez a terça parte dos pontos do time A então fica simples a resolução.Vejamos:

62= 2/3
X= 1/3
basta por na regra de tres:
62 ____ 66%
X 33%
multiplica cruzado 62x33 e divide o resultado por 66.
62x33=2046
2046/66=31

pronto ! time A pontuou 62+31= 93
logo time B pontuou 93/3=31 pontos!
A = Vencedor
B = Perdedor

A fez 62 pontos a mais que B, logo:

A = 62+B

B fez a terça parte dos pontos de A, logo:

B= x/3

Com essas informações teremos:

A = 62 + B
A = 62 + A / 3 O denominador 3 da fração, passa para o outro lado multiplicando o "A".
3A = 62 +A
O "A" do lado direito passara para o outro lado SUBTRAINDO o "3A"
3A - A = 62
2A = 62
A = 62 / 2
A= 31 => esse valor coresponde ao valor de pontos do Time B.
Como a pergunta é qual a pontuação do time perdedor, eu usei as alternativas.

a)
se o perdedor tivesse feito 21 então o vencedor teria feito 21*3 = 63. Logo 63 (pontuação vencedor) - 21 (pontuação perdedor) = 42.

ERRADA pois não bate com a diferença que consta na questão.

b) 31*3 = 93, logo, 93 - 31 = 62. CORRETA.

Então paramos, pois precisamos resolver as outras questões da prova, e o tempo nessa hora vale a aprovação.
Forma mais fácil:

62 + 31= 93
93/3 = 31

Soma o número de pontos pelas alternativas e divide por 3, o resultado que for igual a alternativa é o certo.
A= X
B= X+62, sendo o time vencedor.

O time perdedor fez a terça parte do time vencedor= (x +62)* 1/3. Então a diferença está de 1/3.

x/x+62 = 1/3
3x=x+62
2x=62
x=31
a) 21+62 = 83/3 = 27,6...
b) 31+62 = 93/3 = 31 conta exata

c) 32+6 = 94/3 = 31,3...

d) 42+62 = 104/3 = 34,6...

e) 48+62 = 110/3 = 36,6...

Bem simples! :)
Fiz de um jeito bem simples:

Perdedor : X
Vencedor 62+X

dai eu somei pra encontrar o resultado do X que também é do perdedor
X+62 + X
2X =62
x=31
Foi simples.Peguei 62 dividi por 4 (terça parte=um terço=4)=155 depois subtrai por 62=93 depois dividi por 3(terça parte) =31
Fiz por eliminacao:

time B fez 31 logo o time A fez 93 pois 31+62 = 93

se B fez a terca parte, entao,

31 x 3 = 93 bateu com o resultado do time A
Eu fiz da seguinte forma:

O time perdedor fez " X " pontos e o time vencedor fez " X pontos + 62 "

Podemos então, somar a razão " perdedor + vencedor " e resolver a seguinte equação:

Perdedor + Vencedor
X + (X + 62)
2X = 62
X = 62 : 2
X = 31

Realizando a prova real:
31 + 62 = 93 pontos
dividindo 93 pontos por 3 (que seria a terça parte) = 31
Supondo-se que o time perdedor tenha feito p pontos, o time vencedor fez v = p + 62 pontos. De acordo com o enunciado, p também é igual a v/3, logo p + 62 = 3p donde p = 31 (e v = 93).
Muito fácil, só dividir 62 por 2 = 31.
Pessoal, eu fiz assim!

Já que não entendo matemática, tentei pelas respostas
Ex:
A -) 21 pontos
Somei 21 + 62 = 83 ------ se dividir 83 por 3 (terça parte) não dá a terça parte do total de pontos, ou seja... resposta errada!
B -) 31 pontos
Somei 31 + 62 = 93 ------- se dividir 93 por 3 (terça parte) dá a terça parte do total de pontos, ou seja 93/3 = 31
Resposta certa... 31 pontos foi a quantidade que o time perdedor marcou

Boa sorte a todos!
Eu fiz assim:

Time vencedor "X" pontos.
Time derrotado "X/3" pontos.

x-y= 62
x-(x/3)=62 (substituindo o "y")
3x-x=186
2x=186
X=93 (Time vencedor "93" pontos).

Logo:

X/3 = 93/3 = 31. (Time derrotado "31" pontos)
Eu fiz assim:

X= time vencedor; Y= time perdedor

x=y+62, fica x-y=62 equação I (time vencedor fez sessenta e dois pontos a mais que o time perdedor)

y=1/3*x equação II (Time perdedor fez um terço do total do números de pontos do vencedor)

x-y=62

x-1/3*x=62 (mmc=3)

3x-x=186

2x=186

x=186/2

x=93 (total de pontos do time vencedor)

Agora, substituir em na equação II.

y=1/3*x > y=1/3*93= 31

letra B
Time perdedor = X pontos

Time vencedor = X + 62 pontos

O time perdedor fez a terça parte do total de pontos do time vencedor, ou seja, 1/3 de x+62

X = 1/3 . (X+62)

X = x/3 + 62/3

X = x + 62/3

3x = X + 62

3x - X = 62

2X = 62

X = 62/2

X = 31

OU pela regra de três:

X + 62 ---------- 3/3

X ------------------ 1/3

X = 1/3 . (X+62)

X = x/3 + 62/3

X = 31
Simples!!!!

X = Time forte Y = Time fraco

x = y + 62

y = 1/3.x logo.. (3y = x)

Só substituir!!!

3y = y + 62

2y = 62

Y = 31 Gabarito B
eu fiz mais fácil KSKSKSKS

62/2
=31
b-
Em um jogo de basquete, um dos times, muito mais forte, fez 62 pontos a mais que o seu adversário (x= y + 62), que fez apenas a terça parte do total de pontos feitos pelo time vencedor (x=3y). Nesse jogo, o time derrotado marcou
______________________________________________________________________________
x=y + 62
x = 3y
______________________________________________________________________________
3y = y +62
2y = 62
y = 21

ID

366760

Banca

NCE-UFRJ

Órgão

UFRJ

Ano

2009

Provas

NCE-UFRJ - 2009 - UFRJ - Assistente Administrativo

Disciplina

Matemática

Assuntos

Foram compradas no mês de maio 5 resmas de papel e 3 caixas de giz, gastando-se um total de R$ 71,00. No mês de junho, foram adquiridas do mesmo fornecedor, que manteve os mesmos preços unitários dos produtos, 9 resmas de papel e 6 caixas de giz, gastando-se um total de R$132,00. A diferença entre os preços cobrados por este fornecedor de uma resma e de uma caixa de giz é:

Alternativas

R$ 1,00;

R$ 1,50;

R$ 2,00;

R$ 2,50;

R$ 3,00.

Comentários

É um sistema.
5p + 3g = 71 x(-2) -10p - 6g = -142 5p + 3g= 71 p-g=?
9p + 6g = 132 9p + 6g = 132 3g=21 .: g=7 10-7=3

-p = -10 .: p=10
É uma questão simples de sistema:

Mês Maio -   5 resmas + 3 cxs giz = R$ 71,00
Mês Junho - 9 resmas + 6 cxs giz = R$ 132,00

Separando as informações essenciais já é possível perceber a estrutura do sistema

Então, não podemos resolver um sistema com duas variáveis, temos que escolher uma e eliminar, inicialmente. Eu escolhi eliminar as cxs de giz primeiro e achar logo o valor das resmas.

5r + 3c = 71 multiplica tudo aqui em cima por -2
9r + 6c = 132
-------------------
-10r - 6c = -142
   9r + 6c = 132 agora sim!! dá para cortar uma letra, porque está com valor igual e sinal diferente
--------------------
-1r = -10
    r = 10

Agora que eu achei o valor de uma variável, posso substituir em qualquer expressão. Escolhi substituir na: 5r + 3c = 71

5r + 3c = 71
5.(10) + 3c = 71
50 +3c = 71
3c= 71-50
3c=21
c=7

Achei o valor das resmas e das cxs de giz. Vamos ver o que o autor quer:
"A diferença entre os preços cobrados por este fornecedor de uma resma e de uma caixa de giz é"
r-c = 10-7=3
Resolvendo através de um sistema linear teremos, r = resma e g = giz, assim:

5r + 3g = 71
9r + 6g = 132

Resolvendo o sistema acima pelo método da substituição, encontraremos r = 10 e p = 7.
Fazendo-se a diferença entre ambos, r – g = 3, logo a resposta e R$3,00.

Letra E.
Resma de papel: p
Caixa de giz: g
{5p + 3g = R$ 71,00
{9p + 6g = R$ 132,00

{5p + 3g = R$ 71,00 --> multiplicando por -2: {-10p - 6g = - 142
{9p + 6g = R$ 132,00---------------------------> {9p + 6g = 132

Agora, soma-se as duas equações:

- p = -10
p = 10 ===> g = 7
Portanto, p - g = R$ 3,00
Regra de Cramer:
Considere Resma=R e Giz=G
5R+3G=71
9R+6R=132
R G
Determinante(D)|5 3| =5*6-3*9= 3
|9 6|

Para achar Dr |71 3|= 71*6-3*132=30 entao para achar R é só dividir: Dr/D=30/3=10
|132 6|

Para achar Dg |5 71|= 5*32-71*9=21 então para achar G é só dividir: Dg/D=21/3=7
|9 32|

Logo, a diferença entre Resmas e Giz: 10-7=3

Espero ter ajudado!

ID

395329

Banca

CESPE / CEBRASPE

Órgão

Correios

Ano

2011

Provas

CESPE - 2011 - Correios - Agente de Correios - Atendente Comercial

Disciplina

Matemática

Assuntos

Considerando-se que 3 caixas de encomenda do tipo 2B e 3 caixas de encomenda do tipo flex correios custem, ao todo, R$ 12,00 e que 5 caixas do tipo 2B e 10 do tipo flex correios custem, ao todo, R$ 28,00, é correto afirmar que uma caixa do tipo 2B custa

Alternativas

R$ 2,40.

R$ 3,15.

R$ 3,20.

R$ 1,20.

R$ 2,00.

Comentários

Vou chamar 2B de x e flex de y

Agora vamos montar um sistema de equações

3x + 3y = 12      (vou dividir por -3)
5x+ 10y = 28     (vou dividir por 5)

depois de simplificar, o sistema ficará assim;

- x -   y = - 4
x + 2y = 5,6
          y = 1,6

Agora vamos substituir o valor de y na primeira equação

x = 4 - y
x = 4 - 1,6
x = 2,4
Desculpa mas nao entendi nada do comentario acima... primeiro que na primeira equaçao foram 3 caixas flex e nao 2.... e segundo, como que 4 divido por 3 vai dar 1?

vou mostrar como calculei essa questao, usando as regras de sistemas de equaçoes de 1° grau

vou chamar a caixa 2b de x, e vou chamar a caixa flex de y, logo:

1ª equaçao: 3x+3y=12
2ª equaçao: 5x+10y=28

para deixar apenas uma variavel, vou dividir a primeira equaçao por 3, que vai ficar assim:

x+y=4
5x+10y=28

Como ainda nao da pra calcular uma so variavel, vamos multiplicar a primeira equaçao por -10, ficando assim:

-10x-10y=-40
5x+10y=28

Agora fica facil, é so cortar os valores opostos em y que teremos um sistema simples:

-10x~~-10y~~=-40
5x~~+10y~~=28
||
\/

-10x=-40
5x=28
||
\/

-5x=-12
||
\/

x=12/5

x= 2,40

abraços e bons estudos.
vamos chamar de x as caixas do tipo 2B e de y as do tipo FLEX...

três caixas do tipo 2B = 3x e três caixas do tipo FLEX = 3y somadas custão 12,00 ==> 3x + 3y = 12
cinco caixas do tipo 2B = 5x e dez caixas do tipo FLEX = 10Y   somadas custam 28,00 ==> 5x + 10y = 28

sistema

3x + 3y = 12
5x + 10y = 28

metodo da substituição

3y = 12 - 3x

y = 12 - 3x
          3
____________________________

substituindo y na equação 2

5x + 10(12 - 3x) = 28
                  3

5x + 10(4 - x) = 28

5x + 40 - 10x = 28
5x - 10x = 28 - 40
-5x = -12 . (-1)
5x = 12
x = 12
        5

x = 2,40

x = 2B

então ... solução 2B = 2,40

como o problema não pede o valor de y que é o da caixa flex ,problema resolvido...
Temos um caso de sistema de equação, e é fácil perceber quando ela será usada. Por quê? Bom, sabemos que é uma equação de 1° grau, mas que se resolve por meio de sistemas. Cada equação tem uma incógnita, mas uma equação com duas incógnitas não tem como ser resolvida, porque para cada valor de x podemos calcular um valor diferente para y.
Aqui temos duas incógnitas:
X = 2b
Y = flex
Não possuímos nenhum valor para x ou para y, o que nos leva a pensar em SISTEMAS.
Veja:
1°) 3 caixas do tipo 2b e 3 caixas do tipo flex, ao todo, custam R$ 12,00, então:
3x + 3y = 12
2°) 5 caixas do tipo 2b e 10 caixas do tipo flex, custam R$ 28,00
5x + 10x = 28
Então temos o seguinte sistema:
3x+ 3y = 12
5x + 10y = 28
Vamos simplificar a 1ª equação que é divisível por 3
x + y = 4
5x + 10y = 28
A questão pede o valor da caixa 2b (x), então vamos eliminar o y nesse sistema, multiplicando a 1ª equação por -10:
-10x - ~~10 y~~ = -40
5x + ~~10y~~ = 28
-5x = - 12
x = 2,40
Pelo enunciado tiramos a seguinte conclusão de equações do 1º grau:
Onde: C2b= Caixa do tipo 2B
Cflex= Caixa do tipo flex

3C2b+3Cflex=12 (I)
5C2b+10Cflex=28 (II)

Multiplicamos a primeira equação por (-5) e a segunda por (3) para cancelarmos uma das incógnitas, no caso o C2b:

-15C2b-15Cflex=-60
15C2b+30Cflex=84

Ficando:
15Cflex=84-60
15Cflex= 24
Cflex= R$1,60 (Achamos o valor da Caixa flex)

Agora vamos achar o valor da Caixa 2b:

3C2b+3Cflex=12
3C2b+3*1,6=12
C2b=12-4,8
3
C2b=R$2,40 (Alternativa A)
Meu Deus, quanta repetição!!! Sinceramente.... Gente, ganhar pontos no QC não faz passar em concurso. Dificulta muito quem está lendo os comentários, perda de tempo. Quem lê, pensa que algo de interessante será acrescentado e quando percebe: mil comentários iguais. Paciência.
PS. OBRIGADA A QUEM, REALMENTE, CONTRIBUI.
Sendo caixas 2B = X e caixas Flex = Y, teremos:
3X+3Y=12 SENDO:
3X= -3Y+12
X=-3Y+12 X= -Y+4
3
Na segunda parte do sistema temos a seguinte equação:
5X+10Y=28
Substituindo X na segunda equação teremos:
5.(-Y+4)+10Y=28
-5Y+20+10Y=28
5Y=8 tal que y=8/5
Y=1,60 é o preço da caixa Flex.
X=-Y+4
X= (-1,60)+4
X=2,40 REFERENTE AO PREÇO DA CAIXA 2B
RESPOSTA CERTA: LETRA A
Considerando,
caixa do tipo 2B = x
caixa do tipo flex = y
Tem-se o seguinte sistema:
3x + 3y = 12 eq I
5x + 10y = 28 eq II

Simplificando a eq I:
x + y = 4
y = 4 - x , substituindo na eq II, tem-se:

5x + 10 (4 - x) = 28
5x + 40 - 10x = 28
40 - 5x = 28
5x = 12
x = 2,4

Resposta A)
Fiz pelo metodo dos sistemas lineares e deu certo também. rsrs..que bom que estou entendendo.
joabson silva é um cara esperto demais rsrs

copiou e colou na cara de pau o comentario do professor daqui do qc...rsrrsrs.... esse e cara de pau mesmo kkkkkkk
Uhuuuuuuuuuuuuuuuuuuuuuuu, é bom aprender :)

Fiz pelo método da substituição:

X = 2B

Y = flex

3X + 3Y = 12

5X + 10Y = 28

3X = 12 - 3Y

X = 4 - Y

Substituindo na segunda equação:

5. (4 - Y) + 10.Y = 28

20 - 5Y + 10Y =28

20 + 5Y = 28

5Y = 28 - 20

5Y = 8

Y = 8 / 5

Y = 1,6

Se X = 4 - Y

Agora basta substituir: X = 4 - 1,6

X = 2,40
Copiar o comentário do professor não, mas eu não acho ruim as pessoas comentarem os seus métodos de resolução. Aliás, cada um fez de um jeito, eu fiz de um jeito totalmente diferente de todos comentários e, para muitos, isso pode ser um acréscimo, e não "perda de tempo" como comentou a colega. Felizmente para esse 'problema' é só não abrir os comentários, eu já acho bem massa ver como cada um fez para escolher o melhor método nas que eu erro
Concordo andrea katharina alves barbosa,
Antes de adicionar um comentário verifiquem se já não existe um igual, só comentem se for para colocar macetes, acrescentar algo ou corrigir algum comentário equivocado.

Grata pela compreensão.
Vamos chamar as caixas 2B simplesmente de “B”, e as caixas flex de “F”. Assim,
3 x B + 3 x F = 12
B + F = 4
B = 4 – F
E, também:
5 x B + 10 x F = 28
5 x (4 – F) + 10 x F = 28
20 – 5F + 10F = 28
5F = 8
F = 1,6 real
Portanto, B = 4 – 1,6 = 2,4 reais. Assim, a caixa 2B custa R$2,40.
2B = x
Flex = y

3x + 3y = 12 x(-10) *aqui eu multipliquei por -10 em cima e por 3 em baixo e somei as duas.
5x + 10y = 28 x(3)

-30x - 30y = -120
15x + 30y = 84

15x = 36
x =2,4
Fiz por eliminatória. Começando pela alternativa A :
A Caixa 2B custa 2,40, substitui os valores na equação:

3(caixas) 2B + 3 (caixas) F= 12 reais
3 X 2,40 + 3F = 12 reais
7,20 + 3F = 12
3F= 12 - 7,20
F= 4,80/3
F= 1,60 (Valor da caixa Flex)

Agora substitui com o valor da caixa flex:
3(caixas) 2B + 3 (caixas) F= 12 reais
3 X 2,40 + 3 X 1,60 = 12 reais
7,20 + 4,80 = 12 reais
12 = 12 ou seja, a caixa 2B realmente custa 2,40 como a alternativa A fala.

ID

395344

Banca

CESPE / CEBRASPE

Órgão

Correios

Ano

2011

Provas

CESPE - 2011 - Correios - Agente de Correios - Atendente Comercial

Disciplina

Matemática

Assuntos

Em um escritório, a despesa mensal com os salários dos
10 empregados é de R$ 7.600,00. Nesse escritório, alguns
empregados recebem, individualmente, R$ 600,00 de salário mensal
e os outros, R$ 1.000,00.

Se, para atender a crescente demanda de serviços, o escritório triplicar a quantidade de empregados com salário de R$ 600,00 e duplicar a quantidade de empregados com salário de R$ 1.000,00, então a despesa desse escritório com os salários de seus empregados passará a ser de

Alternativas

R$ 18.800,00.

R$ 18.000,00.

R$ 18.200,00.

R$ 18.400,00.

R$ 18.600,00.

Comentários

Probleminha de função

Recebem R$ 600,00 = A
Recebem R$ 1.000,00 = B

A + B = 10 funcionários
Isolando o A => A = 10 - B
600 A + 1000 B = 7.600,00 salário total deles todos

Substituindo o A:
600 A + 1000 B = 7.600,00
600 . (10 - B) + 1000 B = 7.600,00
6000 - 600 B + 1000 B = 7.600,00
400 B = 1.600
B = 4 funcionários

A + B = 10 A = 10 - 4
A = 6 funcionários

Triplicando a quant. de func. que ganham R$ 600,00 = 6 . 3 = 18 (18 . R$ 600,00 = R$ 10.800,00)
Duplicando a quant. de func. que ganham R$ 1.000,00 = 4 . 2 = 8 (8 . R$ 1.000,00 = R$ 8.000,00)

A soma dos 2: 10.800 + 8.000 = 18.800 (despesa do escritório com os salários dos empregados)

LETRA A
Resolvi assim:

1000 reais x 4 pessoas = 4000,00
10 funcionários - 4 = 6 funcionários

Sobrou 3600 reais / 6 = 600 reais.

3*6=18 x 600 reais = 10.800
2*4=8 x 1000 reais = 8000

Total 18.800
deduzi q se ele tinha 10 funcionarios num total de 7600 reais entao ele deveria ter 6 funcionários ganhando 600 reais e 4 ganhando 1000 totalizando 7600 reais a questão pede q ele triplique a quantidade de funcionários ganhado 600 e duplique a quantidade de funcioários ganhando 1000

agora ficou facil e so triplicar os 6 funcionarios q vão da 18 e multiplicalos por 600 q e o valor q vao receber vai dar um total de 10.800 reais
e duplicar os 4 funcionarios q ganhavam 1000 dara 8 .1000 q vai dar 8000 reais
agora so e so somar 10800 + 8000
totalizando18.800 reais alternativa A
Primeiramente você deve identificar quantos são os funcionários que recebem R$600,00 (x) e quantos são os que recebem R$1.000,00 (y). Sabendo que há um total de 10 funcionários, ou seja, x + y = 10:
600x + 1000y = 7600 (I)
x + y = 10 (II)
Gosto sempre de usar a regra da adição. Nela, sempre uma das incógnitas desaparece e fica mais fácil resolver.
Na questão, eu multipliquei a equação (I) por 1 e a equação (II) por -600, para zerar o x.
600x + 1000y = 7600 (I)
-600x - 600y = -6000 (II) Obs: atentar para o jogo de sinal
Logo, foi zerado o x, e ficou:
400y = 1600
y = 1600/400
y = 4
Agora, é só substituir na equação (II) e achar o x:
x + y = 10 => x + 4 = 10 => x= 10-4 => x=6
Ainda não terminou, agora que você identificou quantos são os funcionários que recebem R$600,00 (x=6) e quantos são os que recebem R$1.000,00 (y=4)
Basta fazer as contas:
triplicar o salário dos que recebem R$600,00.: 600 . 3 = 1800 e multiplicar pela qntd de funcionários 1800 . 6 = 10800
e duplicar o salário dos que recebem R$1.000,00.: 1000.2 = 2000 e multiplicar pela qntd de funcionários 2000 . 4 = 8000
Agora é só somar 10800 + 8000 = 18800.
Letra (A)
por sistema sempre é muito bom.... também consegui a minha assim...
De acordo com o enunciado e considerando x o número de funcionários que recebem 600 reais e y o número de funcionários que recebem 1000 reais, tem-se:
x + y = 10
600x + 1000y = 7600

x = 10 - y
600 (10 - y) + 1000y= 7600
6000 - 600y + 1000y= 7600
400y = 1600
y = 4 funcionários
x = 6 funcionários

De acordo com as novas demandas a soma S dos salários será:
S = (3 . 6 . 600) + (2 . 4 . 1000)
S = 10800 + 8000
S = 18800 reais

Resposta A)
eu tripliquei os 6 funcionários de 600,00 e multipliquei os 4 funcionários de 1,000.

pra dar 7.600 eu descobri que 6 funcionários x 600=3.600 + 4 funcionários x1.000=4.000

agora 3.600 x triplicado ou seja 3.600x3= 10.800

e os 4 funcionarios multipliquei porque 4x1.000 = 4.000x2=8.000 ( deixei pra multiplicar por ultimo)

total: 18.800
x.1000 + y.600 = 7600

x+y = 10

x= 10 -y

logo y =6 e x-4

assi, 3.y.600 + 2.x.1000 = 18800

ID

469216

Banca

CESPE / CEBRASPE

Órgão

Ano

2008

Provas

CESPE - 2008 - ME - Agente Administrativo

Disciplina

Matemática

Assuntos

Um órgão público realizará concurso para provimento
de 30 vagas em cargos de nível médio e superior. O salário
mensal de cada profissional de nível médio será de R$ 1.900,00,
e o de cada profissional de nível superior, de R$ 2.500,00. Os
gastos mensais desse órgão com os salários desses 30
profissionais serão de R$ 67.800,00.

Com relação a essa situação hipotética, julgue os itens que se
seguem.

O número de vagas para profissionais de nível médio no referido concurso será superior a 10.

Alternativas

Certo

Errado

Comentários

Atualização do comentário:

De fato a colega Gisele Silva foi perfeita na resolução, ou seja:

m+s=30

-1900m+2500s=67800

600s=10800

s=18

Se s=18, m=12. Cada um dos 18 profissionais de nível superior receberá 2500 e o total de 45000. Já os 12 profissionais de nível médio receberão, cada um, 1900 e o total de 22800. Ele quer saber se o total de profissionais de nível médio é superior a 10. Item C. São 12.
1900m + 2500 s = 67800

m + s = 30 (-1900)

-1900 m -1900 s = - 57.000

1900 m + 2500 s = 67.800

600 s = 10800

s= 18 =========> m = 12 ( e não 10 do médio)
X1900 + Y 2500 = 67800 Sabe-se que : X + Y = 30 ----> ENTÃO X = 30 - Y
(30-Y) . 1900 + 2500Y = 67800
57000 - 1900 Y + 2500 Y = 67800
600Y = 10800
Y =10800/ 600
Y = 18

Logo :

X = 12

ID

469219

Banca

CESPE / CEBRASPE

Órgão

Ano

2008

Provas

CESPE - 2008 - ME - Agente Administrativo

Disciplina

Matemática

Assuntos

Sistemas Lineares

O órgão público deverá gastar, mensalmente, menos de R$ 42.000,00 com os salários dos novos profissionais de nível superior, caso eles sejam contratados.

Alternativas

Certo

Errado

Comentários

ERRADO

Montando uma função teremos: EM (Ensino Médio) e S (Superior)

1900.EM + 2500.S = 67800

EM + S = 30

Isolando EM, EM = 30 - S

1900 . (30 -S) + 2500.S = 67800

57000 - 1900.S + 2500.S = 67800

600.S = 10800

S = 10800/600

S = 18 , agora sabemos que temos 18 funcionários com nível Superio e 12 funcionários com Nível Médio.Multiplicado a quantidade de funcionários pelo salário teremos: 18 . 2500 = 45000 e 12 . 1900 = 22800.
A FORMA MAIS RÁPIDA, PRINCIPALMENTE EM UMA PROVA DE CONCURSO.

REGRA DE CRAMER:

DET. Y

1900 67800
1 30
_______________= 10800 / 600 = 18. SUBSTITUINDO. 250X18= 45.000
1900 25000
1 1
Não precisa nem montar equações, é só testar o valor informado na questão. Dividir os 42.000 por 2.500 que é o valor do salário dos cargos de nível superior, não dá divisão exata, logo a afirmativa está errada pois não dá pra ter um número de cargos que seja decimal, tem de ser um número inteiro.

ID

486415

Banca

CESGRANRIO

Órgão

BNDES

Ano

2008

Provas

CESGRANRIO - 2008 - BNDES - Técnico Administrativo - Inglês

Disciplina

Matemática

Assuntos

Considere que, em uma empresa, há máquinas copiadoras do tipo A e do tipo B, nas seguintes condições:

• 3 máquinas do tipo A, funcionando conjuntamente com 2 máquinas do tipo B, produzem 13.920 cópias, ao todo, em meia hora;
• todas as máquinas do tipo A funcionam sob um mesmo regime constante;
• todas as máquinas do tipo B funcionam sob um mesmo regime constante, 40% maior do que o regime das máqui- nas do tipo A.

O número de cópias por minuto, nessa empresa, que uma máquina do tipo B faz a mais do que uma máquina do tipo A é

Alternativas

Comentários

3A+2B=13920 EM 30 MIN
B=A+40%A
B=A+40/100A ai voces simplificam a fração ai fica
B=7A/5

NO PRIMEIRO SISTEMA VOCE ISOLA O B AI FICA
3A+2B=13920
2B=13920-3A
B=13920-3A/2
AI VOCE SUBSTITUI O VALOR ENCONTRADO DE B=7A/5
A=2400
B=3360
AI E SO DIVIDIR POR 30 PARA SABER O QUE FOI PRODUZIDO EM 1 MINUTO AI FICA
A=112
B=80
A DIFERENÇA DOS DOIS 112-80=32 QUE E A RESPOSTA CORRETA
Fala galera!

1º passo: Devemos analisar a questão ->

Temos 3 maquinas de A que produzem X cópias cada e 2 de B que produzem X+40% cópias ou X+0,4x = 1,4x

2º Passo: Montar a equação -> 3X+2*1,4x = 13920 -> 5,8x = 13920 -> X = 2400 cópias a cada 30 minutos envolvendo A e B.

Sabemos que as máquinas B produzem 40% a mais do que as máquinas A, logo, 40% de 2400 = 40/100*2400 = 960 Páginas a cada 30 minutos.

Para descobrir quantas páginas por minuto B produz a mais, basta dividir 960/30 = 32

Gabarito >> D)
Vamos lá.

Sabemos que B produz 40% a mais que A, então a equação pode ser:
2(1,4A) + 3(A) = 13920
2,8A + 3A = 13920
5,8A = 13920
A = 2400
Logo, cada máquina A produz 2400 cópias.

Se B = 1,4A
Entâo B = 1,4 * 2400
B = 3360

Dividindo A e B por 30 minutos, temos:
A = 2400/30 B = 3360/30
A = 80 B = 112

112 - 80 = 32

Nesse caso a resposta é letra D.

ID

492490

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2008

Provas

CESGRANRIO - 2008 - BR Distribuidora - Técnico de Administração e Controle Júnior

Disciplina

Matemática

Assuntos

15“A MBR, em um ano de contrato com o Orla Rio, coletou 15.519 litros de óleo de cozinha nos 309 quiosques das praias cariocas. A matéria-prima deu origem a 3 toneladas de sabão pastoso.”

Jornal O Globo, 22 jul. 2008.

Considere que a quantidade de óleo coletada nos primeiros seis meses tenha correspondido à metade da quantidade coletada nos últimos seis meses, mais 618 litros. Quantos litros de óleo foram coletados nos primeiros seis meses?

Alternativas

4.967

5.585

6.687

8.334

9.934

Comentários

x + y = 15519

x = y/2 + 618

y/2 + 618 + y = 15519 (MMC)

y + 1236 + 2y = 31038

3y = 29802

y = 9934

x + 9934 = 15519

x = 5585
A questão em tela versa sobre a disciplina de Matemática e o assunto inerente à equação.

Tal questão apresenta os seguintes dados os quais devem ser utilizados para a sua resolução:

1) A MBR, em um ano de contrato com o Orla Rio, coletou 15.519 litros de óleo de cozinha nos 309 quiosques das praias cariocas.

2) A matéria-prima deu origem a 3 toneladas de sabão pastoso.

3) Considere que a quantidade de óleo coletada nos primeiros seis meses tenha correspondido à metade da quantidade coletada nos últimos seis meses, mais 618 litros.

Por fim, frisa-se que a questão deseja saber quantos litros de óleo foram coletados nos primeiros seis meses.

Resolvendo a questão

Para fins didáticos, irei chamar de "x" a quantidade de óleo de cozinha coletada nos primeiros seis meses e de“y” a quantidade de óleo de cozinha coletada nos últimos seis meses.

Neste tipo de questão, é interessante resolvê-la por partes.

Na primeira parte, é descrita a informação de que "A MBR, em um ano de contrato com o Orla Rio, coletou 15.519 litros de óleo de cozinha nos 309 quiosques das praias cariocas". Assim, é possível representar tal parte por esta equação:

1) x + y = 15.519.

Isolando-se a variável “y”, tem-se o seguinte:

1) y = 15.519 - x.

Na terceira parte, é descrita a informação de que "Considere que a quantidade de óleo coletada nos primeiros seis meses tenha correspondido à metade da quantidade coletada nos últimos seis meses, mais 618 litros". Assim, é possível representar tal parte por esta equação:

2) x = (y/2) + 618.

Substituindo-se o valor de “y” encontrado na equação “1”, na equação “2”, tem-se o seguinte:

x = (y/2) + 618, sendo que y = 15.519 - x

x = ((15.519 - x)/2) + 618 (multiplicando-se tudo por “2”, para se eliminar o denominador)

2x = 15.519 - x + 1.236

x + 2x = 15.519 + 1.236

3x = 16.755

x = 16.755/3

x = 5.585 litros de óleo.

Logo, nos primeiros seis meses, foram coletados 5.585 litros de óleo.

Gabarito: letra "b".

ID

515926

Banca

Exército

Órgão

EsPCEx

Ano

2008

Provas

Disciplina

Matemática

Assuntos

A soma das idades dos amigos Pedro, José e Ivo é igual a 60. Sabe-se que a soma da idade de José com a diferença entre as idades de Pedro e Ivo (nesta ordem) é igual a 30 e que o dobro da idade de Pedro mais a idade de José, menos a idade de Ivo é igual a 55. Assim, a idade de José é

Alternativas

Comentários

P + J + I = 60
J + P - I = 30 ----> J + P = 30 + I
2P + J - I = 55
J + P + I = 60
30 + I + I = 60
2I = 30
I = 15
2P + J - 15 = 55
2P + J = 70
P + J = 45 .(-2)
2P + J = 70
-2P - 2J = -90
-J = -20 .(-1)
J = 20 Anos
GABARITO: LETRA C
Prep querendo ajudar o candidato

ID

545212

Banca

CESGRANRIO

Órgão

PETROQUÍMICA SUAPE

Ano

2011

Provas

Disciplina

Matemática

Assuntos

Sistemas Lineares

Desde o ano de 2009, os brasileiros podem mudar de operadora de telefonia, sem necessidade de alterar os números de seus telefones. Dezembro de 2010 foi o mês com maior volume de troca de operadoras, tanto na telefonia fixa quanto na telefonia móvel, totalizando 463 mil transferências. Se, nesse mês, o número de transferências na telefonia móvel correspondeu ao dobro do número de transferências realizadas na telefonia fixa, menos 26 mil, quantos milhares de transferências de operadora de telefonia móvel foram realizadas em dezembro de 2010?

Alternativas

163

189

215

300

326

Comentários

Fiz da seguinte forma:
F = telefonia fixa
M = telefonia móvel
A questão diz que o número de transferências da telefonia móvel foi o dobro do número de transferências da telefonia fixa, menos 26 mil.
Nesses termos, temos que M = 2F - 26.
Logo, é possível montar a seguinte equação:
2F -26 + F = 463
3F -26 = 463
3F = 463 + 26
3F = 489
F = 489/3
F = 163
Portanto, o número de transferências da telefonia fixa foi de 163 mil. Como o número de transferências da telefonia móvel corresponde ao dobro, menos 26 mil, desse número, temos que M = 2.163 -26.
M = 2.163 -26
M = 326 -26
M = 300
A questão em tela versa sobre a disciplina de Matemática e o assunto inerente à equação.

Tal questão apresenta os seguintes dados os quais devem ser utilizados para a sua resolução:

1) Desde o ano de 2009, os brasileiros podem mudar de operadora de telefonia, sem necessidade de alterar os números de seus telefones.

2) Dezembro de 2010 foi o mês com maior volume de troca de operadoras, tanto na telefonia fixa quanto na telefonia móvel, totalizando 463 mil transferências.

3) Nesse mês de Dezembro de 2010, o número de transferências na telefonia móvel correspondeu ao dobro do número de transferências realizadas na telefonia fixa, menos 26 mil.

Por fim, frisa-se que a questão deseja saber quantos milhares de transferências de operadora de telefonia móvel foram realizadas em dezembro de 2010.

Resolvendo a questão

Para fins didáticos, irei chamar de "x" o número de transferências na telefonia móvel e de “y” o número de transferências realizadas na telefonia fixa.

Neste tipo de questão, é interessante resolvê-la por partes.

Na segunda parte, é descrita a informação de que "Dezembro de 2010 foi o mês com maior volume de troca de operadoras, tanto na telefonia fixa quanto na telefonia móvel, totalizando 463 mil transferências". Assim, é possível representar tal parte por esta equação:

1) x + y = 463.000.

Isolando-se a variável “y”, tem-se o seguinte:

1) y = 463.000 - x.

Na terceira parte, é descrita a informação de que "Nesse mês de Dezembro de 2010, o número de transferências na telefonia móvel correspondeu ao dobro do número de transferências realizadas na telefonia fixa, menos 26 mil". Assim, é possível representar tal parte por esta equação:

2) x = 2y - 26.000.

Substituindo-se o valor de “y” encontrado na equação “1”, na equação “2”, tem-se o seguinte:

x = 2y - 26.000, sendo que y = 463.000 - x

x = (2 * (463.000 - x)) - 26.000

x = 926.000 - 2x - 26.000

x + 2x = 926.000 - 26.000

3x = 900.000

x = 900.000/3

x = 300.000.

Logo, no mês de Dezembro de 2010, foram realizadas 300.000 (trezentos mil) transferências de operadora de telefonia móvel.

Gabarito: letra "d".

ID

545743

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2011

Provas

Disciplina

Matemática

Assuntos

De acordo com o Relatório de Sustentabilidade de 2009, as empresas de uma holding concentravam, nas Regiões Centro-Oeste e Norte, 2.464 funcionários no final daquele ano. Mas a diferença entre o número de funcionários lotados nas duas regiões era considerável. Se 128 novos funcionários fossem efetivados na Região Centro-Oeste, esta passaria a ter metade do número de funcionários da Região Norte. Sendo assim, quantos funcionários trabalhavam em empresas da holding, na Região Norte, no final de 2009?

Alternativas

736

1.104

1.360

1.558

1.728

Comentários

C.O + N = 2464 >>>> Total
(C.O + 128)x2 = N >>>> Se contratassem mais 128 funcionários o nº deles na região Centro-Oeste seria a metade da região Norte
C.O + 2C.O + 256 = 2464>>>>> A equação
C.O = 736>>>> O resultado Centro-Oeste
N = 2464 - 736
N = 1728>>>> A quantidade de funcionários da região Norte
Centro-Oeste = Y       Norte = X
1ª) X+ Y = 2.464
2ª) Y + 128 = X/2     Logo, encontramos: X= 2y + 256
Vamos substituir o valor de X na Primeira equação:
2y + 256 +y = 2.464
3y = 2.464 - 256    =           y = 1.728/3 =       Y = 736
Voltemos à Segunda equação:
X = 2Y + 256

X = 2 * 736 + 256      X = 1472 + 256 = 1728
C + N = 2464

C + 128 = N/2

N = 2C + 256

C + 2C + 256 = 2464

3C = 2208

C = 736

736 + N = 2464

N = 1728
A questão em tela versa sobre a disciplina de Matemática e o assunto inerente à equação.

Tal questão apresenta os seguintes dados os quais devem ser utilizados para a sua resolução:

1) De acordo com o Relatório de Sustentabilidade de 2009, as empresas de uma holding concentravam, nas Regiões Centro-Oeste e Norte, 2.464 funcionários no final daquele ano. Mas a diferença entre o número de funcionários lotados nas duas regiões era considerável.

2) Se 128 novos funcionários fossem efetivados na Região Centro-Oeste, esta passaria a ter metade do número de funcionários da Região Norte.

Por fim, frisa-se que a questão deseja saber quantos funcionários trabalhavam em empresas da holding, na Região Norte, no final de 2009.

Resolvendo a questão

Para fins didáticos, irei chamar de "x" a quantidade de funcionários que trabalhavam na Região Centro-Oeste e de “y” a quantidade de funcionários que trabalhavam na Região Norte.

Neste tipo de questão, é interessante resolvê-la por partes.

Na primeira parte, é descrita a informação de que "De acordo com o Relatório de Sustentabilidade de 2009, as empresas de uma holding concentravam, nas Regiões Centro-Oeste e Norte, 2.464 funcionários no final daquele ano. Mas a diferença entre o número de funcionários lotados nas duas regiões era considerável". Assim, é possível representar tal parte por esta equação:

1) x + y = 2.464.

Isolando-se a variável “x”, tem-se o seguinte:

1) x = 2.464 - y.

Na segunda parte, é descrita a informação de que "Se 128 novos funcionários fossem efetivados na Região Centro-Oeste, esta passaria a ter metade do número de funcionários da Região Norte". Assim, é possível representar tal parte por esta equação:

2) x + 128 = y/2.

Substituindo-se o valor de “x” encontrado na equação “1”, na equação “2”, tem-se o seguinte:

x + 128 = y/2, sendo que x = 2.464 - y

2.464 - y + 128 = y/2

-y + 2.592 = y/2 (passando o “2” para o outro lado multiplicando)

-2y + 5.184 = y

-2y - y = -5.184

-3y = -5.184 (multiplicando-se tudo por “-1”)

3y = 5.184

y = 5.184/3

y = 1.728.

Logo, o número de funcionários que trabalhavam em empresas da holding, na Região Norte, no final de 2009, corresponde a 1.728.

Gabarito: letra "e".

ID

559840

Banca

CESGRANRIO

Órgão

CITEPE

Ano

2011

Provas

Disciplina

Matemática

Assuntos

No refeitório de uma fábrica, há exatamente 36 mesas, algumas com 6 cadeiras, e as demais, com 10 cadeiras. Sabendo-se que, ao todo, há 300 cadeiras nesse refeitório, quantas são as mesas com 10 cadeiras?

Alternativas

Comentários

X = mesa com 6 cadeiras

Y = mesa com 10 cadeiras

x + y = 36

x = 36 - y

6x + 10y = 300

6 ( 36 - y ) + 10y = 300

216 - 6y + 10y = 300

4y = 300 - 216

y = 84/4

y = 21
A questão em tela versa sobre a disciplina de Matemática e o assunto inerente à equação.

Tal questão apresenta os seguintes dados os quais devem ser utilizados para a sua resolução:

1) No refeitório de uma fábrica, há exatamente 36 mesas, algumas com 6 cadeiras, e as demais, com 10 cadeiras.

2) Ao todo, há 300 cadeiras nesse refeitório.

Por fim, frisa-se que a questão deseja saber quantas são as mesas com 10 cadeiras.

Resolvendo a questão

Para fins didáticos, irei chamar de "x" a quantidade de mesas com 6 cadeiras e de “y” a quantidade de mesas com 10 cadeiras.

Neste tipo de questão, é interessante resolvê-la por partes.

Na primeira parte, é descrita a informação de que "No refeitório de uma fábrica, há exatamente 36 mesas, algumas com 6 cadeiras, e as demais, com 10 cadeiras". Assim, é possível representar tal parte por esta equação:

1) x + y = 36.

Isolando-se a variável “x”, tem-se o seguinte:

1) x = 36 - y.

Na segunda parte, é descrita a informação de que "Ao todo, há 300 cadeiras nesse refeitório". Assim, é possível representar tal parte por esta equação:

2) 6x + 10y = 300.

Substituindo-se o valor de “x” encontrado na equação “1”, na equação “2”, tem-se o seguinte:

6x + 10y = 300, sendo que x = 36 - y

6 * (36 - y) + 10y = 300

216 - 6y + 10y = 300

10y - 6y = 300 - 216

4y = 84

y = 84/4

y = 21.

Logo, a quantidade de mesas com 10 cadeiras corresponde a 21.

Gabarito: letra "d".

ID

600157

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2011

Provas

Disciplina

Matemática

Assuntos

Ação global contra petróleo caro

A Agência Internacional de Energia (AIE), formada por 28 países, anunciou ontem a liberação de 60 milhões de barris de petróleo de reservas estratégicas [...].
Os EUA vão entrar com metade do volume, [...] a Europa irá colaborar com 3/10, e o restante virá de Austrália, Japão, Coreia e Nova Zelândia.

O Globo, Rio de Janeiro, p. 17. 24 jun. 2011. Adaptado.

Suponha que os países asiáticos (Japão e Coreia) contribuam juntos com 1,8 milhão de barris a mais do que a contribuição total dos países da Oceania (Austrália e Nova Zelândia). Desse modo, quantos milhões de barris serão disponibilizados pelos países asiáticos?

Alternativas

5,2

5,6

6,9

7,4

8,2

Comentários

Total liberado: 60mi

EUA: 30mi (metade de 60mi)
UE: 18mi (3/10 de 60mi)
ÁSIA&OCEANIA: 12mi (restante)

Sendo:

ÁSIA: X
OCEANIA: Y

X + Y = 12mi
X = Y + 1,8mi

Y = 10,2mi
X = 6,9mi (alternativa "C")
EUA=60m/2=30m
Europa=3/10*60m=18
Asia/Oc.=X
Total=60m

x/2+3/10=4x/5

4x/5-x=x/5

Asia/Oc=x/5 ->12m.

Asia= Oceania + 1,8

X+X+1,8=12

2x=20,2
x=5,1

Asia= 5,1+1,8=6,9

Oceania=5,1
Asia=6,9 c)
Colegas, não entendi as contas... Poderiam explicar mais os valores finais.

Estou engatinhando quando o assunto é matemática... Valeu
Na verdade o cálculo do nosso amigo em primeiro está correto, apenas ele se equivocou no final em trocar os valores de X e Y.

Na questão ele informa que metade dos 60 milhões é o EUA que vai participar, e três décimos ou seja, 60 / 10 = 6 e 6 x 3 = 18. Até este momente nós temos um total de 48 milhoes. Para completar os 60 basta diminuir 60 de 48 temos: 12.

Com o 12 agora podemos trabalhar.

12 milhoes serão divididos em Japao, Coreia, Austrália e Nova Zelandia (Você ja calcula 3 milhoes para cada), so que ele informa que Japao e Coreia contribuirão com 1,8milhoes a mais que os outros 2.

Podemos chamar de X os paises Asiáticos, e de Y os países da Oceania. Então temos:

Os países asiáticos(X) contribuirão com o que os paises da Ocenia(Y) irão contribuir mais 1,8:

X = Y + 1,8

E sabemos que os asiáticos(X) e os da Oceania(Y) totalizam 12:

X+Y = 12

Agora é so fazer os cálculos:

Se x+y =12 então:
x = 12-y

Substituimos o X na primeira função temos:

12-y = y + 1,8
-y-y = 1,8-12
-2y= -10,2 (Multiplica -1)
2y = 10,2
y= 10,2/2 = 5,1

Até aqui sabemos que Y(Oceania) irá contribuir com 5,1 Milhoes de Barris

Ora, se sabemos que eles contribuirão com 5,1 então é so pegar o total destes quatros países(12) e subtrair dos 5,1 que obtivemos:

Y = 5,1

Y = x +1,8
mesmo que dizer:
x = y+1,8
x = 5,1+1,8
x=6,9

Agora sim! Sabemos que Japao e Coreia contribuirão com 6,9 Milhões de barris! :)

Espero ter ajudado!
Oi Bruno, valeu!!! Ótima explicação.
Perdão por ter invertido as letras ao final, Priscila!.
Obrigado pela correção, Bruno!
Resp. C = 6,9
Total disponibilizado = 60 mi => EUA metade 1/2 x 60 = 30 mi. e Europa = 3/10 x 60 = 18 mi.
dos 60 mi. Restou 12 mi. 60 - (30+18). Como existem 1,8 mi. a mais (ref. ao japão e coreia q doaram a mais)
Finalmente temos: 12 + 1,8 = 13,8 Logo, 13,8 / 4 = 3,45 para cada país, são eles: Japão, Coreia, Austrália e Nova Zelândia.
(Japão + Coreia) = 2 x 3,45 = 6,9
تواصل الكفاح
Total: 60

EUA: metade de 60 = 30

Europa: 3/10 de 60 = 18

Ásia e Oceania: 30 - 18 = 12

A + O = 12

A = O + 1,8

O + 1,8 + O = 12

2O = 12 - 1,8

2O = 10,2

O = 5,1

A + 5,1 = 12

A = 12 - 5,1

A = 6,9
A questão em tela versa sobre a disciplina de Matemática e o assunto inerente à interpretação de problemas numéricos e à equação.

Tal questão apresenta os seguintes dados os quais devem ser utilizados para a sua resolução:

1) A Agência Internacional de Energia (AIE), formada por 28 países, anunciou ontem a liberação de 60 milhões de barris de petróleo de reservas estratégicas.

2) Os EUA vão entrar com metade do volume. Logo, os EUA entrarão com 30 milhões de barris (60 milhões dividido por "2").

3) A Europa irá colaborar com 3/10. Logo, a Europa irá colaborar com 18 milhões de barris (60 milhões multiplicado por "3/10").

4) O restante virá de Austrália, Japão, Coreia e Nova Zelândia. Subtraindo o total de barris (60 milhões) dos valores encontrados acima (30 milhões e 18 milhões), descobre-se que o valor restante corresponde a 12 milhões de barris, sendo tal valor o que será contribuído por Austrália, Japão, Coreia e Nova Zelândia.

5) Os países asiáticos (Japão e Coreia) irão contribuir juntos com 1,8 milhão de barris a mais do que a contribuição total dos países da Oceania (Austrália e Nova Zelândia).

Por fim, frisa-se que a questão deseja saber quantos milhões de barris serão disponibilizados pelos países asiáticos.

Resolvendo a questão

Para fins didáticos, irei chamar de "x" o valor correspondente à contribuição dos países asiáticos (Japão e Coreia) e de "y" o valor correspondente à contribuição dos países da Oceania (Austrália e Nova Zelândia).

Sabendo que os países asiáticos (Japão e Coreia) irão contribuir juntos com 1,8 milhão de barris a mais do que a contribuição total dos países da Oceania (Austrália e Nova Zelândia), então é possível representar tal informação por meio da seguinte equação:

1) x = 1,8 + y.

Nesse sentido, sabendo que o restante da contribuição virá de Austrália, Japão, Coreia e Nova Zelândia e que tal restante corresponde a 12 milhões de barris, então é possível representar tal informação por meio da seguinte equação:

2) x + y = 12.

Substituindo a equação "1", na equação "2" encontrada acima, tem-se o seguinte:

x + y = 12, sendo que x = 1,8 + y

1,8 + y + y = 12

2y = 12 - 1,8

2y = 10,2

y = 10,2/2

y = 5,1 milhões de barris.

Logo, os países da Oceania (Austrália e Nova Zelândia) irão contribuir com 5,1 milhões de barris.

Substituindo o valor encontrado acima, na equação "1", tem-se o seguinte:

x = 1,8 + y, sendo que y = 5,1

x = 1,8 + 5,1

x = 6,9 milhões de barris.

Logo, os países asiáticos (Japão e Coreia) irão contribuir com 6,9 milhões de barris.

Gabarito: letra "c".

ID

611503

Banca

COPEVE-UFAL

Órgão

Prefeitura de Penedo - AL

Ano

2010

Provas

COPEVE-UFAL - 2010 - Prefeitura de Penedo - AL - Agente Administrativo - 1

Disciplina

Matemática

Assuntos

Em um sítio, Marcos cria cavalos e galinhas. Multiplicando o número de cavalos por quatro e somando nove obtemos o número de galinhas existente no sítio. Sabendo-se que entre esses animais a quantidade de pés é 186, podemos afirmar que

Alternativas

existem 65 galinhas no sítio.

o número de galinhas é um número par.

o número de cavalos é múltiplo de seis.

o número de galinhas é menor que o número de cavalos.

existem 21 cavalos no sítio.

Comentários

x = cavalos
y = galinhas

o enunciado nos diz que;

4x + 9 = y
4x + 2y = 186

Podemos resolver através de um sistema de equações

4x - y = - 9 ( vou multiplicar por -1)

Montado o sistema temos;

- 4x +   y = 9
4x + 2y = 186
           3y = 195
             y = 65 galinhas
____________________________

4x + 9 = y
4x = y - 9
4x = 65 - 9
x = 56/4
x = 14 cavalos

ID

616675

Banca

FCC

Órgão

MPE-SE

Ano

2010

Provas

Disciplina

Matemática

Assuntos

Relativamente aos candidatos inscritos num dado Concurso, sabe-se que o total supera 10 000 unidades e a razão entre o número de mulheres e o de homens, nesta ordem, é igual a 4/5. Assim sendo, se o total de candidatos for o menor possível, de quantas unidades o número de homens inscritos excederá o de mulheres inscritas?

Alternativas

1 112.

1 118.

1 124.

1 128.

1 132.

Comentários

GABARITO: LETRA A (1.112)

(I) M + H = X (não sabemos quantos candidatos são, apenas que eles ultrapassam 10.000).

            M = X - H

(II) M = 4

      H   5

Substituindo (I) em (II) temos:

X - H = 4

H    5

5X - 5H = 4H

H = 5X

        9

Agora, vamos substituir o H na primeira equação (I):

M = X - H

M = X - 5X

             9

M = 4X

        9

Agora temos os valores de M e H. O exercício pede qual a diferença entre o número de inscritos homens (5X/9) e mulheres (4X/9):

H - M = 5X - 4X = X

             9      9     9

Bom, então descobrimos que a diferença entre homem e mulheres é X. O exercício traz que o número mínimo de inscritos é superior a

                                                                                                          9

10.000 e que o total de candidatos é o menor possível. Portanto, como temos que a diferença entre homens e mulheres é um número divisível por 9 (X/9), devemos achar o menor número possível superior a 10.000 que seja divisivel por 9:

10.000 = x

10.001 = x

10.002 = x

10.003 = x

10.004 = x

10.005 = x

10.006 = x

10.007 = x

10.008 = ✓

Achamos então o menor número divisível por 9 e maior que 10.000 que é 10.008. Ou seja, foram inscritos 10.008 (valor do X lá na equação (I)) pessoas neste concurso.

Logo,

X (diferença entre homens e mulheres) = 10.008 = 1.112

9                                                             9

ID

620815

Banca

CONSULPLAN

Órgão

Correios

Ano

2008

Provas

CONSULPLAN - 2008 - Correios - Agente de Correios - Atendente Comercial

Disciplina

Matemática

Assuntos

Carlos e sua irmã Renata foram com seu cachorro Jerry ao veterinário. Lá, encontraram uma balança com defeito que só indicava corretamente “pesos” superiores a 60kg. Assim, eles “pesaram” dois a dois e obtiveram as seguintes marcas:
• Carlos e Jerry juntos: 87kg.
• Carlos e Renata juntos: 123kg.
• Renata e Jerry juntos: 66kg.
Quantos quilogramas pesa o cachorro Jerry?

Alternativas

72kg

51kg

12kg

15kg

24kg

Comentários

c: Carlos; r: Renata; j: Jerry temos que
c + j = 87(a); c + r = 123(b); r + j = 66(c).
desenvolvendo (b) temos;
c = 123 - r;
substituindo em (a), temos;
(123 - r) + j = 87; j = 87 - (123 - r ); j = -36 + r (d);
desenvolvendo (c) temos j = 66 - r (e);
Ao juntarmos (d) e (e) temos um sistema;
j = -36 + r
j = 66 - r; (somando as duas expressões temos);
2j = 30 j = 15 kg.
C+J=87
C+R=123 (*-1)
R+J=66

C+J=87
-C-R=-123
R+J=66

Soma de equações

2J=87+66-123
2J=153-123
2J=30
j=30/2
j=15Kg
simples demais, sabemos que a diferença do peso de Carlos e Renata é de 21kg (87kg - 66kg), então fazemos: x + (x-21) = 123,
logo x= 72 kg (CARLOS), então faz: 87 - 72 = 15. Caso queira conferir, faça com o peso da RENATA x - 21 que será 72 - 21 = 51kg,
e confirme o resultado: 66 - 51 = 15
Fiz da seguinte forma:

Se C+J=87kg e C+R= 123kg, então a R pesa 36kg (123 - 87) a mais do que o J. Sendo assim

x + (x+36) = 66 (foi dito que R+J=66)
2x = 66-36
x = 30/2
x = 15

J = 15
da maneira mais facil, sem fórmulas:

Carlos e Jerry juntos: 87kg.
• Carlos e Renata juntos: 123kg.
• Renata e Jerry juntos: 66kg

somei os pesos de Carlos e Jerry com os de Renata e Jerry, depois diminui de Carlos e Renata e dividi por 2 porque Jerry estava sendo contado 2 vezes.

87 + 66 = 153 - 123 = 30 / 2 = 15
Fiz da seguinte foma:

C+J= 87 *(-1)
C+R=123
R+J=66
--------------------------
-C-J= -87
C+R=123
R+J=6
---------------------
R +R=102
2R=102
R=102/2
51

R+J=66
51+J=66
J=66-55
J 15
C +J = 87
C+ R = 123 Multiplica por - 1
R+J = 66
--------------- soma tudo
2J =30
J=15
Primeiro, pegamos as informações que tem J(jerry):

Carlos e Jerry juntos: 87kg

Renata e Jerry juntos: 66kg

Quando somamos esses dois valores, temos Jerry somado duas vezes + Carlos + Renata:

2J+C+R = 153kg

Para deixarmos apenas o valor dos dois Jerrys, precisamos tirar o valor de C+R, que é dado na questão: 123kg

153-123 = 30

Então, temos que:

2J = 30

J = 30/2

J = 15
C + J = 87

C + R = 123

R + J = 66

C = 87 - J

R = 123 - C

J = 66 - R

J = 66 - 123 + 87 - J

2J = 30

J = 15

ID

648673

Banca

PaqTcPB

Órgão

Prefeitura de Patos - PB

Ano

2010

Provas

PaqTcPB - 2010 - Prefeitura de Patos - PB - Professor - Matemática

Disciplina

Matemática

Assuntos

A conta de luz de Zequinha é composta por uma taxa mensal, igual para todos os usuários, mais o que deve pagar pela quantidade de kWh gastos no mês. Na conta do mês de janeiro, Zezinho pagou R$ 57,50 por 95 kWh gastos. Já na conta do mês de fevereiro, ele pagou R$ 62,50 por 105 kWh gastos. Qual o valor da taxa mensal paga pelos consumidores?

Alternativas

R$ 9,00.

R$ 9,50.

R$ 10,00.

R$ 10,50.

R$ 11,00.

Comentários

Gabarito C.

Dados da questão:

-Pagou 57,50 por 95 Kw.
-Pagou 62,50 por 105 Kw.

Perceba que da primeira conta para a segunda, aumentaram 10 Kw (105 - 95 = 10Kw) e 5,00 (62,50 - 57,50 = 5,00). Esse 5,00 é o valor dos 10 Kw, então, para descobrir o valor de um Kw, divida 5 por 10 = 0,50 centavos por Kw.

Como é 0,50 por Kw, para saber o valor da taxa fixa, basta pegar 95 e multiplicar por 0,5 = 47,50. Esse valor é o valor apenas dos Kw, o que faltar para o total da conta será a taxa fixa: 57,50 - 47,50 = 10,00.

ID

648697

Banca

PaqTcPB

Órgão

Prefeitura de Patos - PB

Ano

2010

Provas

PaqTcPB - 2010 - Prefeitura de Patos - PB - Professor - Matemática

Disciplina

Matemática

Assuntos

Tranquilino tem o sétuplo da idade de seu filho. Trinta anos depois, Tranquilino terá apenas o dobro da idade de seu filho. Qual a idade de Tranquilino quando seu filho nasceu?

Alternativas

20 anos.

22 anos.

24 anos.

26 anos.

28 anos.

ID

651301

Banca

PaqTcPB

Órgão

Prefeitura de Patos - PB

Ano

2010

Provas

PaqTcPB - 2010 - Prefeitura de Patos - PB - Técnico de Informática - Administração

Disciplina

Matemática

Assuntos

Seu Gustavo gastou R$ 60,00 para pagar as contas de água e luz. Sabendo que a conta de luz era igual a 60% da conta de água, determine o valor da conta de água.

Alternativas

R$ 37,50.

R$ 40,00.

R$ 30,00.

R$ 32,50.

R$ 22,50.

Comentários

x + 6x/10 = 60

(5x+3x)/5 = 60

x=300/8 -> 37.5

ID

651322

Banca

PaqTcPB

Órgão

Prefeitura de Patos - PB

Ano

2010

Provas

PaqTcPB - 2010 - Prefeitura de Patos - PB - Técnico de Informática - Administração

Disciplina

Matemática

Assuntos

A soma das idades dos dois filhos de Tiêta é, atualmente, 50 anos. Quando o filho mais novo nasceu, o mais velho tinha 1/3 da idade que tem hoje. Quais as idades dos filhos de Tiêta?

Alternativas

17 anos e 33 anos.

18 anos e 32 anos.

19 anos e 31 anos.

20 anos e 30 anos.

21 anos e 29 anos.

Comentários

d-

Se Ele nasceu quando 1 ja tinha 1/3 da idade atual, o mais novo é 2/3 da idade do mais velho.

x+ 2/3x = 50

5x/3 = 50

x = 30.

y = 20

ID

663175

Banca

CS-UFG

Órgão

UFG

Ano

2010

Provas

CS-UFG - 2010 - UFG - Vestibular - Prova 01

Disciplina

Matemática

Assuntos

O dono de uma loja de brinquedos gastará R$ 75.000,00 para comprar 5.000 unidades, entre bolas, jogos e bonecas, de um fabricante. O custo unitário das bolas é R$ 10,00 e dos jogos, R$ 15,00, enquanto o preço das bonecas ainda está em negociação com o fabricante. O dono da loja não sabe ainda qual a quantidade exata que irá comprar de cada brinquedo, pois isso depende da venda de seu estoque, mas sabe que a quantidade de bolas deve ser o dobro da quantidade de bonecas.
Com base nestas informações, o preço unitário de cada boneca, para que as quantidades de cada brinquedo que o dono da loja pode adquirir nesta compra fiquem indeterminadas, deve ser:

Alternativas

R$ 10,00

R$ 15,00

R$ 20,00

R$ 25,00

R$ 30,00

ID

684667

Banca

UEG

Órgão

UEG

Ano

2007

Provas

UEG - 2007 - UEG - Vestibular - Prova 1

Disciplina

Matemática

Assuntos

Sistemas Lineares

Uma conta no valor de R$ 195,00 foi paga com cédulas de dois, cinco, dez e de vinte reais, totalizando 30 cédulas. Juntando-se as cédulas de cinco com as de dez reais usadas no pagamento, obteve-se um total de dez cédulas, e a quantidade das cédulas de vinte reais usadas foi de um terço do número de cédulas de dois reais. A quantidade de cédulas de cinco reais usadas para o pagamento da conta foi

ID

691438

Banca

UDESC

Órgão

UDESC

Ano

2011

Provas

UDESC - 2011 - UDESC - Vestibular - Prova 1

Disciplina

Matemática

Assuntos

Sistemas Lineares

Uma rede de cinemas localizada em um Shopping Center oferece a seus clientes filmes em tecnologia 3D e filmes tradicionais (tecnologia 2D) a preços respectivos de 22 e 16 reais cada ingresso. Durante um único final de semana, esta rede faturou 18.840 reais com a venda de 1200 ingressos. Seus funcionários constataram que um terço dos clientes que optaram por assistir a filmes tradicionais e um quarto dos clientes que escolheram filmes em 3D nesse final de semana eram estudantes e/ou pessoas com idade igual ou superior a 60 anos, por isso pagaram meia- entrada ao adquirir seus ingressos.
Portanto, o total de ingressos vendidos com valor integral, durante esse final de semana, foi igual a:

Alternativas

840

360

720

480

910

ID

713665

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2011

Provas

CESGRANRIO - 2011 - Petrobras - Engenheiro de Equipamento Júnior - Elétrica 2011

Disciplina

Matemática

Assuntos

Um sistema linear formado por n equações referentes a n incógnitas pode ser reescrito na forma matricial A_nxn .X_nx1 = B_nx1 , onde A_nxn ,X_nx1 e B_nx1 são, respectivamente, as matrizes dos coeficientes do sistema, das incógnitas e dos termos independentes. Dizer que tal sistema é possível e determinado é o mesmo que dizer que a matriz

Obs.:
A^T_{n x n} é a transposta de A _{n x n}
A^-1_{n x n} é a inversa de A _{n x n}

Alternativas

A_nxn é simétrica.

A_nxn é invertível.

A_nxn tem posto menor do que n.

X_nx1 = B_nx1.A ^-1 _nxn

X_nx1 = A ^T _nxn . B _nx1

Comentários

Se o sistema é possível e determinado:
Anxn*Xnx1=Bnx1
(A^-1 nxn)Anxn*Xnx1=(A^-1 nxn)*Bnx1
Xnx1=A^-1 nxn*Bnx1

Assim, a equação só terá solução se A^-1 nxn existir, ou seja, Anxn deve ser invertível.
B

ID

719161

Banca

UFSCAR

Órgão

UFSCAR

Ano

2007

Provas

UFSCAR - 2007 - UFSCAR - Vestibular - Prova 2

Disciplina

Matemática

Assuntos

Uma loja vende três tipos de lâmpada (x, y e z). Ana comprou 3 lâmpadas tipo x, 7 tipo y e 1 tipo z, pagando R$ 42,10 pela compra. Beto comprou 4 lâmpadas tipo x, 10 tipo y e 1 tipo z, o que totalizou R$ 47,30. Nas condições dadas, a compra de três lâmpadas, sendo uma de cada tipo, custa nessa loja

Alternativas

R$ 30,50.

R$ 31,40.

R$ 31,70.

R$ 32,30.

R$ 33,20.

Comentários

Montando o sistema
3x + 7y + z = 42,10 I
4x+10y + z = 47,30 II
-------------------------------------------------------------------------------
Agora multiplicamos a equação I por 3 e a II por (-2)
3x + 7y + z = 42,10 *3
4x+10y + z = 47,30 *(-2)
----------------------------------------------------------------------------
9x + 21y + 3z = 126,30 I
-8x - 20y - 2z = -94,60 II
_________________________________
x + y + z = 31,70 Somando a I pela II

Portanto:
x + y + z = 31,70

letra C

ID

758845

Banca

CESGRANRIO

Órgão

CMB

Ano

2012

Provas

CESGRANRIO - 2012 - CMB - Assistente Técnico Administrativo - Apoio Administrativo

Disciplina

Matemática

Assuntos

Os números m e n são racionais e tais que m + 5n = 5 e 4m + 10n = 16.

Qual o valor de m + n?

Alternativas

9,4

7,9

5,5

3,4

2,6

Comentários

Vamos lá, montando o sistema teremos:
m + 5n = 5 (isolando) m = 5 - 5n (*)
4m + 10n = 16 (**)
Usando (*) em (**), teremos:
4 (5 - 5n) + 10n = 16
20 - 20n + 10n = 16
-10n = 16 - 20
-10n = - 4
n = 4
10
n = 0,4
Jogando o valor de n em (*), teremos:
m = 5 - 5 * 0,4
m = 5 - 2
m = 3
Como a questão pede a soma de m + n, então 3 + 0,4 = 3,4
Letra D.
m+5n=5-> m=-5n+5
4m+10n=16-> 4*(5n+5)+10n=16->n=2/5

m=-5n+5
m=5*(2/5)+5
m=3

m+n=3+2/5-> 15/5+2/5=17/5

17/5->3,4
Podemos resolver assim:

m+5n=5
4m+10n=16

m+5n=5 *(-2)
4m+10n=16

-2m-10n=-10
4m+10n=16

2m=6
6/2=3 m=3

Substituindo:

m+5n=5

3+5n=5

5n=5-3=2
n=2/5
n=0,4
m+n=3+0,4=3,4

Questão D
m + 5n = 5 (m = 5 - 5n)

4m + 10n = 16
4 (5 - 5n) + 10n = 16
20 - 20n + 10n = 16
20 - 10n = 16
- 10n = 16 - 20
- 10n = - 4 . (- 1)
10n = 4
n = 4/10
n = 0,4

m + 5n = 5
m + 5 . 0,4 = 5
m + 2 = 5
m = 5 - 2
m = 3

m + n = 3 + 0,4 = 3,4
Olá galera do QC, este exercício resolvi através de sistemas.
M+5N=5
4M+10N=16
deste modo usei o método da substituição
M=5-5N e assim substitui na outra equção
4M+10N=16 M=5-5X2/5
4(5-5N)=16 M=3
20-20N=16 2/5+3= 3,4 Alternativa C
N=2/5
De acordo com o enunciado, tem-se:

m + 5n = 5 eq I

4m + 10n = 16 eq II

m = 5 – 5n

4 ( 5 – 5n) + 10n = 16

20 – 20n + 10n = 16

-10n = 16 – 20

-10n = -4

n = 0,4

m = 5 – 5 x 0,4 = 5 – 2 = 3

m = 3

Finalizando,

m + n = 3 + 0,4 = 3,4

RESPOSTA: (D)
1. Descobrir o valor de "m" e substituir na outra equação:
m+5n=5
m=5-5n
2. Substituindo "m" na outra equação e encontrando o "n"
4m+10n=16
4.(5-5n)+10n=16
20-20n+10n=16
20-10n=16
20-16=10n
4=10n
n=0,4
3. Substituindo "n" na primeira equação a fim de descobrir o valor de "m".
m+5n=5
m+5.0,4=5
m+2=5
m=5-2
m=3
Final. Efetuar a soma de "m"+ "n", conforme pede o exercício:
n=0,4
m=3
m+n=3,4
GABARITO: D.
Isso é sistema de equações.
Já deram o sistema pronto kkkkk.
Gostei dessa!
Mais fácil impossível.
m + 5n = 5
4m + 10n = 16

Resolvendo por substituição:
m + 5n = 5 -> m=5 - 5n
4m + 10n = 16 -> 20 - 20n+10n = 16 -> -10n=-4 -> n=2/5
m=5 - 5n -> m=5-2 -> m=3

Achando a resposta:
m+n = 2/5+3 = 3,4
m+5n = 5

4m + 10n = 16

m=5-5n

4(5-5n) + 10n = 16

20 - 20n + 10n = 16

-10n = -4

n= -4/-10

n=2/5

m=5-5(2/5)

m=5-10/5

m=25-10/5

m=15/5

m=3

m+n

3+2/5

15+2/5 = 17/2= 3,4

ID

796126

Banca

UNEMAT

Órgão

UNEMAT

Ano

2011

Provas

UNEMAT - 2011 - UNEMAT - Vestibular - Prova 1

Disciplina

Matemática

Assuntos

A professora Ana Maria precisa comprar 80 unidades de material para a sua aula, entre eles, lápis, canetas e cadernos. Espera comprar os lápis a R$ 1,00 cada, as canetas a R$ 2,00 e os cadernos a R$ 4,00. Arrecadou dos alunos R$ 230,00 para esta compra.

Se o número de cadernos deve ser igual ao número de lápis e canetas juntos, a solução para esta compra será:

Alternativas

40 lápis, 35 canetas e 5 cadernos

5 lápis, 35 canetas e 40 cadernos

10 lápis, 30 canetas e 40 cadernos

20 lápis, 20 canetas e 40 cadernos

15 lápis, 25 canetas e 40 cadernos

ID

802696

Banca

Marinha

Órgão

COLÉGIO NAVAL

Ano

2010

Provas

Marinha - 2010 - COLÉGIO NAVAL - Aluno - 1° Dia

Disciplina

Matemática

Assuntos

Dois números reais não simétricos são tais que a soma de seus quadrados é 10 e o quadrado de seu produto é 18. De acordo com essas informações, a única opção que contém pelo menos um desses dois números é:

Alternativas

{x ∈ ℜ | - 1 ≤ x ≤ 1 }

{x ∈ ℜ | - 1 ≤ x ≤ 3 }

{x ∈ ℜ | 3 ≤ x ≤ 5 }

{x ∈ ℜ | 5 ≤ x ≤ 7 }

{x ∈ ℜ | 7 ≤ x ≤ 9 }

ID

814543

Banca

AOCP

Órgão

TCE-PA

Ano

2012

Provas

AOCP - 2012 - TCE-PA - Técnico de Informática - Suporte

Disciplina

Matemática

Assuntos

Para estimular os estudos em matemática, um pai fez a seguinte proposta à filha: “A cada problema resolvido corretamente, você receberá R$ 5,00 e, a cada problema resolvido erroneamente, você deverá pagar uma multa de R$ 2,00". Após resolver 30 problemas, a filha recebeu R$ 122,00. Quantos problemas ela acertou?

Alternativas

Comentários

GABARITO C

A= acertos

B= erros

A+B= 30 ( A= 30-B)

5A-2B= 122

5(30-B) - 2B = 122

150-5B - 2B= 122

-7B= -28

B= 4

A= 30 - 4

A= 26
A + B= 30 OBS. Não sabe quanto vale cada um, porém sabemos o total, logo igualar a ele.

5A - 2B = 122,00 OBS. Agora sabemos quanto vale cada um, porém não sabemos a quantidade de cada um.

A + B= 30

B= 30 - A OBS. Esta é a razão para calcular o valor.

5A - 2B = 122,00

5A - 2(30 - A) = 122,00

5A - 60 + 4A = 122,00

7A= 182,00

A= 26 OBS. É o total de acerto.

Gabarito: C
Alguém com outra sugestão para resolver a questão? ainda possuo dúvidas.
Fiz diferente:

pensei assim: Chegar mais perto do valor dividindo por 5 (valor q ela recebia por acerto)

O que chegou mais perto (com resto divisivel por 2 --- o valor da multa)

130/5 = 26 acertos
A= Acertos
E= Erros

5A - 2E = 122

O número de acertos é a quantidade de questões menos os erros .
A= (30- E) =122

5A . (30-E) - 2E = 122
150 - 5E - 2E= 122
7E = 150 - 122
7E= 28
E= 28/7

E= 4

Depois de descobrir a quantidade de questões erradas você vai diminuir pelo total.

A= 30 - 4

A= 26

Resposta item C
a soma e mais pratico de resolve esse sistema

cada certa ela recebe 5 e cada errada ela estona 2 no caso -2

vou POR ( c) pra certa e( E) PARA errada! certo

C + E = 30 (2)
5C -- 2E = 122

2C +2E = 60

5C -- 2E=122

REGUA DO CORTE NO SIMETRICOS ENTAO FICA E SOMA :

7C=182
C=182/7
C=26
A + E = 30 (2) Multiplica para conseguir eliminar os erros.
5A - 2E = 122

2A + 2E = 60
5A - 2E = 122

7A = 182
A = 182 / 7
A = 26

OBS: Veja que eu multipliquei a primeira equação por 2 para poder eliminar os erros assim trabalhar somente com os acertos. Espero ter ajudado.
Caso ela tivesse acertado tudo, ganharia 150 reais
Vamos lá:

Se ela ganhou 122 reais
150 - 122 = 28 reais

28 dividido pela soma dos reais (5+2) ou seja 28/7 dá 4
Temos a constante.

Se ela errou 4
Então 30-4 = 26 acertos

GAB C
A questão em tela versa sobre a disciplina de Matemática e o assunto inerente à equação.

Tal questão apresenta os seguintes dados os quais devem ser utilizados para a sua resolução:

1) Para estimular os estudos em matemática, um pai fez a seguinte proposta à filha: “A cada problema resolvido corretamente, você receberá R$ 5,00 e, a cada problema resolvido erroneamente, você deverá pagar uma multa de R$ 2,00."

2) Após resolver 30 problemas, a filha recebeu R$ 122,00.

Por fim, frisa-se que a questão deseja saber quantos problemas a filha acertou.

Resolvendo a questão

Para fins didáticos, irei chamar de "c" a quantidade de problemas que a filha acertou e de “e” a quantidade problemas que a filha errou.

Neste tipo de questão, é interessante resolvê-la por partes.

Sabendo que a filha resolveu, ao todo, 30 problemas, então é possível representar tal parte por esta equação:

1) c + e = 30.

Isolando-se a variável “e” acima, tem-se o seguinte:

1) e = 30 - c.

Nesse sentido, sabendo que a filha recebeu R$ 122,00, que, a cada problema resolvido corretamente, pela filha, ela receberá R$ 5,00 e que, a cada problema resolvido erroneamente, pela filha, ela deverá pagar uma multa de R$ 2,00, então é possível representar tal parte por esta equação:

2) 5c - 2e = 122.

Substituindo, na equação “2”, o valor de “e”, encontrado na equação “1”, tem-se o seguinte:

5c - 2e = 122, sendo que e = 30 - c

5c - (2 * (30 - c)) = 122

5c - 60 + 2c = 122

7c - 60 = 122

7c = 122 + 60

7c = 182

c = 182/7

c = 26.

Logo, a filha acertou 26 questões.

Gabarito: letra "c".

ID

830893

Banca

VUNESP

Órgão

SPTrans

Ano

2012

Provas

Disciplina

Matemática

Assuntos

Três amigas A, B e C subiram juntas em uma balança de farmácia e esta marcou 106,5 kg. Quando apenas duas delas A e C permaneceram sobre a balança, esta marcou 72,3 kg. Antes de saírem da farmácia, as amigas B e C subiram novamente nessa balança, e esta marcou 68,8 kg. Das três amigas, a mais pesada e a mais leve são, respectivamente,

Alternativas

A e C.

A e B.

B e C.

C e B.

C e A

Comentários

Do enunciado:

A + B + C = 106,5 (1)
A + C = 72,3 (2)
B + C = 68,8 (3)

Substituindo (2) em (1):

A + C + B = 106,5
72,3 + B = 106,5
B = 34,2 Kg.

Substituindo B em (3):

B + C = 68,8
34,2 + C = 68,8
C = 34,6 Kg.

Substituindo C em (2):

A + C = 72,3
34,6 + A = 72,3
A = 37,7 Kg.

A é a MAIS PESADA.
B é a MAIS LEVE.

ALTERNATIVA B.

ID

833953

Banca

CESGRANRIO

Órgão

DECEA

Ano

2012

Provas

CESGRANRIO - 2012 - DECEA - Controlador de Tráfego Aéreo Código

Disciplina

Matemática

Assuntos

Dentre as unidades do DECEA, há quatro Centros Integrados de Defesa Aérea e Controle de Tráfego Aéreo (CINDACTA). Dois desses Centros, o CINDACTA III e o CINDACTA IV, são responsáveis pelo controle e gerenciamento do espaço aéreo de uma área que totaliza 18,7 milhões de km² . A área de atuação do CINDACTA III, entretanto, é bem maior que a do IV, superando em 3,1 milhões de km² o dobro da área de atuação do CINDACTA IV.
Sendo assim, qual é, em milhões de km², a área de atuação do CINDACTA III?

Alternativas

5,2

7,8

10,9

11,5

13,5

Comentários

Por coveniência, chame-mos CINDACTA III = III; CINDACTA IV = Iv.
III+IV=18,7; simplificando IV = 18,7-III(I);
"A área de atuação do CINDACTA III, entretanto, é bem maior que a do IV, superando em 3,1 milhões de km² o dobro da área de atuação do CINDACTA IV". Em números fica assim;
III=2Iv+3,1 (II)
Substituindo (I) em (II) temos;
III = 2(18,7-III)+3,1
III=37,4-2III+3,1
III+2III= 40,5
3III = 40,5
III = 13,5
Chamamos de CINDACTA III como X e CINDACTA IV como Y para facilitar nosso entendimento. Assim temos:
X+Y=18,7
X=2y+3,1
Logo substituindo:
X+Y=18,7
(2Y+3,1)+Y=18,7
2Y+Y=18,7 - 3,1
3Y=15,6
Y= 5,2
18,7 - 5,2 = 13,5
Resposta correta letra E.
Bons Estudos!

ID

849064

Banca

COMVEST - UNICAMP

Órgão

UNICAMP

Ano

2011

Provas

COMVEST - UNICAMP - 2011 - UNICAMP - Vestibular - Prova 1

Disciplina

Matemática

Assuntos

As companhias aéreas costumam estabelecer um limite de peso para a bagagem de cada passageiro, cobrando uma taxa por quilograma de excesso de peso. Quando dois passageiros compartilham a bagagem, seus limites são considerados em conjunto.
Em um determinado voo, tanto um casal como um senhor que viajava sozinho transportaram 60 kg de bagagem e foram obrigados a pagar pelo excesso de peso. O valor que o senhor pagou correspondeu a 3,5 vezes o valor pago pelo casal.
Para determinar o peso excedente das bagagens do casal (x) e do senhor que viajava sozinho (y), bem como o limite de peso que um passageiro pode transportar sem pagar qualquer taxa (z), pode-se resolver o seguinte sistema linear:

ID

913423

Banca

FCC

Órgão

DPE-SP

Ano

2013

Provas

FCC - 2013 - DPE-SP - Oficial de Defensoria Pública

Disciplina

Matemática

Assuntos

Certa manhã de um domingo ensolarado, Cléo combinou encontrar-se com seu namorado às 11 horas, no Parque do Ibirapuera. Ela calculou que, se percorresse de bicicleta o trajeto de sua casa ao Parque, rodando à velocidade média de 10 km/h, chegaria ao local do encontro exatamente 30 minutos após o horário combinado; entretanto, se a velocidade média da bicicleta fosse de 15 km/h, ela chegaria ao local do encontro exatamente 30 minutos antes das 11 horas. Diante do exposto, a que velocidade média Cléo deverá rodar em sua bicicleta para que possa se encontrar com seu namorado exatamente às 11 horas?

Alternativas

12 km/h.

12,25 km/h.

12,5 km/h.

13 km/h.

13,25 km/h.

Comentários

A distância é sempre a mesma, é o segredo da questão.
Se v = d/t (fórmula da velocidade), d=vt.

Temos 3 velocidades com seus 3 tempos, sendo a distância sempre igual. 2 velocidades são dadas, 10km/h e 15km/h, e a outra é a resposta que procuramos.
Vamos supor (v1,t1) para quando ela chega meia hora depois (v2, t2) para quando chega meia hora antes e (v3,t3) para quando chega na hora certa, 11h.

Observe que como a distância é sempre a mesma, podemos escrever: d1 = d2 = d3, o que corresponde a
v1*t1 = v2*t2 = v3*t3

Temos o v1 e v2.
Vamos achar t3 e com isso t2 e t1 e achar depois v3.

Supondo t3 = xh. Decorre disso que t2 = t3 - 1/2 h e t1 = t3 + 1/2h, certo?

Vamos substituir na equação negritada os seguintes dados (só as duas primeiras partes, sem o v3*t3):
v1 = 10
v2 = 15
t2 = t3 - 1+2 (aqui vamos tirar o "h" de hora porque como os dois lados são hora, podemos cortar e vira só matemática, sem as unidades da física)
t1 = t3 + 1/2

10(t3+1/2) = 15 (t3-1/2) fazendo a álgebra chega-se a t3 = 2,5, com isso sabemos que t1 = 3 e t2 = 2

Pronto! Deixo o resto para vocês...

Tá bom, se eu deixar o resto vão achar que ficou ruim, pegamos duas partes da equação, sendo uma necessariamente v3*t3 e substituimos, por exemplo:
v3*t3 = v1*t1
v3*2,5 = 10*3, de onde se acha v3=12, que é a RESPOSTA!!
de um modo mais simples:

10km/h --- distância d --- tempo t
logo: 10=d/t ; d=10t.
15km/h --- distância d --- tempo t-1
logo: 15=d/t-1 ; d=15t-15
igualando as equações: 10t=15t-15 ; t=3h ; d=30
vejamos que a questão quer exatamente às 11h, meia hora antes do tempo t inicial.
logo, v'=d/t' ; v'=30/2,5= 12km/h

Letra "a"
isso é física!
V = d/t → d = v.t

v1 = d/t →10=d/t → d=10t

v2=D/t-1 → 15=d/t-1 → d=15t-15

D1 = D2 = D3

Primeiro: D1 = D2 → 10t=15t-15

15=15t-10t → 5t=15 → t = 3

d=10t → d= 10+3= 30

v1.t1 = v2.t2

10 (t3+1/2) = 15 (t3-1/2)

t3 = 2,5

V = d/t → V3 = 30/2,5 = 12
Demorei mas consegui!
Fiz assim:
Sabemos que D = V/T, certo? Logo temos duas expressões para D:
D = 10.(T+30) e D= 15 (T-30), pois quando ela anda a 10km/h ela faz em MAIS 30 MIN e quando ela anda a 15km/h ela faz em MENOS 30 MIN.
Ambas se referem a mesma distância, logo: 10(T+30) = 15(T-30). Vamos resolver?
10T + 300 = 15T - 450 >>> 15T-10T = 300 + 450 >>> 5T = 750, logo T = 150 minutos!
Aplicando em alguma das expressões acima podermos descobrir a distância.
D = 10 (T+30) >>> D=10(150+30) >>> D = 10.180 >> D=1800 KM!!!
Ora, se sabemos D e sabemos T, só nos falta saber V, a variável que o problema quer:
1800 = V.150 >> 1800/150 = V, então V = 12! RESPOSTA: LETRA A! :)
Para solucionar a questão o ideal seria que o candidato relembrasse conceitos de Mecânica Clássica, como por exemplo, velocidade = espaço / tempo. Entretanto, os cálculos matemáticos exigidos se restringem basicamente à aplicação da Regra de Três Simples.

No primeiro cálculo da ciclista:

10 km --------------- 1hora

D km ---------------- T horas

Assim, 10 T = D

No segundo cálculo, a distância é a mesma porém o tempo é menor.

15 km --------------- 1hora

D km ---------------- (T – 1) horas

Assim, 15 (T - 1) = D → 15T – 15 = D

Resolvendo o sistema, tem-se:

10T = D

15T – 15 = D

Assim,

10T = 15T – 15

T = 3 horas

D = 30 km

De posse do valor da distância D, é possível resolver o problema, pois como considerou-se 11h30min como T, sabe-se que 11h = T – 0,5 = 3 – 0,5 = 2,5

Sendo assim,

X km --------------- 1 hora

30Km--------------- 2,5 horas

Assim,

2,5 X = 30 → X = 12

Portanto a velocidade média da ciclista deve ser 12km/h.

(Resposta A)
Bom, fiz de um jeito mais simples:

Para facilitar, coloquei como se 11 horas fosse a hora X

Assim: na velocidade 10 km/h se fazem em X+30
            na velocidade de 15km/h se fazem em X-30

Temos então uma regra de três simples, sendo que as grandezas são INVERSAS (pois quanto maior a velocidade, menor o tempo gasto.
Então:
10k/h------ X+30
15k/h ------X-30
Como são grandezas Inversas, não multiplicamos em cruz, e sim em reta!
Então temos:
10 (X+30) = 15 (X-30) ->> 10x + 300 = 15x -450 ->> 5x=750 ->> x= 150

Logo, a 10k/h------ X+30 = 180 ou a 15km/h -------X-30 = 120

Agora basta fazer uma regra de três para saber a velocidade chegando no tempo X (que é 150) que estipulamos, que seria o tempo de 11 horas. Para isso podemos trabalhar com qualquer uma das velocidades, ou na de 10km/h ou na de 15 km/h.
Escolhi a de 10km/h
Então:
10km/h -----180
     V     -----150

Como tempo e velocidade sao grandezas inversas, multiplicamos em linha reta. Logo, 1800= 150v ->> V= 12

Espero que tenha ajudado
v = d / t => d = v x t

t1 = t3 + 30min ; t2 = t3 - 30min

d1 = d2
v1t1 = v2t2
10 (t3 + 0,5) = 15 (t3 - 0,5)
10t3 + 5 = 15t3 - 7,5
5 + 7,5 = 15t3 - 10t3
12,5 = 5t3
2,5 = t3

v1t1 = 10 (t3 + 0,5) = 10 (2,5 + 0,5) = 10 x 3 = 30

v1t1 = v3t3
30 = v3 x 2,5
v3 = 30 / 2,5
v3 = 12
Gente, pelo amor de Deus, sério que não tem como resolver por regra de três, tem que usar essa fórmula de física? Como eu vou lembrar fórmula de física na hora da prova? :/
A física está em tudo, a fórmula a qual se refere é uma simples regra de três

10 km - 1 hora
X km - t - 0,5 hr

assim fica:

10km / 1 hora = X km / t - 0.5hr

é o mesmo que

v=S/T
v = d / t => d = v x t
t= 30 min = 0,5 horas
d1 = d2
v1t1 = v2t2
10 (t + 0,5) = 15 (t - 0,5)
10t + 5 = 15t - 7,5
10t-15t = -7,5 - 5
-5t = -12,5 x (-1)
t = 12,5/5
t = 2,5 h
Como d1 = d2 não muda nos dois percursos, e iguando os tempos com +0,5 e - 0,5, encontramos o tempo da chegada no tempo correto 2,5 horas, precisamos da distância, igualando novamente.
d1 = v2t2
d1 = 15 (2,5 - 0,5)
d1 = 15 x 2
d1 = 30
v = d / t
v = 30 / 2,5
v = 12 km/h
10km+30m=15km-30m
10km-15km= -30m-30m
-5km= -60m (-1)
60m/5km
Km=12

ID

938725

Banca

VUNESP

Órgão

CETESB

Ano

2013

Provas

VUNESP - 2013 - CETESB - Escriturário

Disciplina

Matemática

Assuntos

Ana foi à padaria comprar pãezinhos, porém levou pouco dinheiro, e percebeu que se comprasse 12 pãezinhos ficaria faltando R$ 0,60, mas se comprasse 10 pãezinhos receberia R$ 0,50 de troco. Ana levou à padaria

Alternativas

R$ 5,50.

R$ 6,00.

R$ 6,50.

R$ 7,00.

R$ 7,50.

Comentários

Sendo x o preço do pão:
12x-0.6=dinheiro levado por Ana
10x+0.5=dinheiro levado por Ana

Igualando:
12x-0.6=10x+0.5 <-> x=0.55

Logo o pão custa 55 centavos, substituindo em quaisquer das equações se chega ao dinheiro levado por maria, 6 reais.
ela tem x dinheiro para gastar itens custando y e o troco é a diferença. Destarte, temos uma subtração.

X-12Y=-0,60
X-10Y=0,50
X=12Y-0,60
12Y-0,60-10Y=0,50
2Y=1,10
Y=0,55
X=12*(0,55)-0,60
X=6,00
Tenho R$ 0,50 e para ficar devendo -R$ 0,60 quanto tenho que gastar?
+0,50 ______________________ -0,60

Gastei R$0,50 fiquei com zero; gastei + 0,60 e fiquei devendo os R$0,60. No total gastei R$1,10
Como o enunciado disse na primeira hipótese 12 pães, falta-me R$0,60
E na segunda hipótese 10 pães, sobra-me R$0,50
A diferença entre os valores é de R$1,10 e 2 pães. Logo, cada pão custa R$0,55
Se cada pão custa R$0,55 e ela comprou 10 (R$5,50) e sobraram R$0,50; Ana levou R$6,00
12x = y + 0,60
y = 12x - 0,6

10x = y - 0,50
y = 10x + 0,5

12x - 0,6 = 10x + 0,5
2x = 1,1
x = 0,55

y = 10x + 0,5
y = 5,5 + 0,5
y = 6
--------------------- > B
12p-0,60=10p+0,50

12p-10p=0,50+0,60

2p=1,10/2

p=0,55
X-12P=-0,60 .(-5)

X-10P=0,50 .(6)

-5X+60P=3

6X-60P=3

X=6

GAB: B

FORÇA E HONRA SEMPRE!!!

ID

938731

Banca

VUNESP

Órgão

CETESB

Ano

2013

Provas

VUNESP - 2013 - CETESB - Escriturário

Disciplina

Matemática

Assuntos

Sistemas Lineares

Uma pessoa foi a uma papelaria e comprou 2 pastas grandes, 3 pastas médias e 1 pasta pequena, pagando, no total, R$ 21,20. Se tivesse comprado 3 pastas grandes, 2 pastas médias e 1 pasta pequena, teria gastado R$ 22,80, mas se tivesse comprado 3 pastas de cada tamanho teria gastado R$ 30,00. A diferença de preço entre a pasta mais cara e a pasta mais barata era

Alternativas

R$ 4,80.

R$ 4,50.

R$ 3,20.

R$ 3,00.

R$ 2,80.

Comentários

Pasta grande = x
Pasta média = y
Pasta pequena = z

2x + 3y +z = 21,20
3x + 2y +z = 22,80
3x + 3y + 3z = 30

Simplificando:

2x + 3y +z = 21,20
3x + 2y +z = 22,80
x + y + z = 10

Montando a matriz e escalonando:

|2 3 1 21,20|
|3 2 1 22,80|
|1 1 1 10|

|1 1 1 10|
|2 3 1 21,20|
|3 2 1 22,80|

L2 = L2 - 2L1
L2 = 2 - 2 = 0
L2 = 3 - 2 = 1
L2 = 1 - 2 = -1
L2 = 21,20 - 20 = 1,20

|1 1 1 10|
|0 1 -1 1,2|
|3 2 1 22,80|

L3 = L3 -3.L1
L3= 3 - 3 = 0
L3 = 2 -3 = -1
L3 = 1 -3 = -2
L3 = 22,8 - 30 = -7,2

|1 1 1 10|
|0 1 -1 1,2|
|0 -1 -2 -7,2|

L3 = L3 + l2
L3 = 0+0= 0
L3 = -1+1 = 0
L3 = -2-1 = -3
L3 = -7,2 + 1,2 = -6

|1 1 1 10|
|0 1 -1 1,2|
|0 0 -3 -6|

Transformando em equação novamente:

x + y + z = 10
--- y - z = 1,2
----- -3z = -6

-3x = -6
z = -6/-3
z = 2

y - z = 1,2
y = 1,2 + 2
y = 3,2

x + y + z = 10
x +3,2 +2 =10
x = 10 -5,2
x = 4,8

Resposta:
Pasta grande custa R$4,80
Pasta média custa R$ 3,20
Pasta pequena custa R$ 2,00
R$4,80 - R$ 2,00=R$ 2,80
Alternativa correta letra E
ADOTANDO: P=PASTA PEQUENA,M=PASTA MÉDIA,G=PASTA GRANDE

1)2G+3M+1P=21,20 >> P=21,20-(2G+3M) >> P=21,20-2G-3M;
2)3G+2M+1P=22,80 >> P=22,80-(3G+2M) >> P=22,80-3G-2M;
3)3G+3M+3P=30,00 >> 3P=30-(3G+3M) >> 3P=30-3G-3M >> 3P=3.(10-G-M) >> P=3.(10-G-M)/3 >> P=10-G-M

SUBSTITUINDO 3 EM 1 TEMOS 4:
4) 1-M0-G=21,20-2G-3M >> -G+2G-M=3M=21,20-10 >> G+2M=11,20 >> G=11,20-2M

SUBSTITUINDO 3 EM 2 TEMOS 5:
10-G-M=22,80-3G-2M >> -G+3G-M+2M=22,80-10 >> 2G+M=12,80 >> M=12,80-2G

SUBSTITUINDO 4 EM 5 :
M=12,80-2(11,20-2M) >> M=12,80-22,40+4M >> 3M=9,60 >> M=3,20

SABENDO O VALOR DA PASTA MÉDIA PODEMOS OBTER O PREÇO DAS DE MAIS:
G=11,20 - 2.3,20 >> G=4,80
P= 10-4,80-3,20 >> P=2,00

A DIFERENÇA ENTRE A MAIS CARA E A MAIS BARATA:
G-P >> 4,80-2,00 = 2,80

RESPOSTA ALTERNATIVA "E"

ID

939388

Banca

CESGRANRIO

Órgão

Petrobras

Ano

2012

Provas

Disciplina

Matemática

Assuntos

Na lanchonete de seu João, vende-se “suco” de uva e “refresco” de uva, ambos preparados com água e um concentrado da fruta, mas em diferentes proporções.
O “suco” é preparado com três partes de concentrado e duas partes de água, enquanto o “refresco” é obtido misturando-se uma parte de concentrado a três de água. Certa manhã, utilizando 19 litros de concentrado e 22 litros de água, seu João preparou x litros de “suco” e y litros de “refresco” de uva.

A diferença entre essas quantidades, em litros, correspondeu a

Alternativas

Comentários

C = concentrado, A = água.
3C + 2A = 1 suco
1C + 3A = 1 refresco.

vamos agrupar os concentrados de um lado e a água de outro. Assim temos;
3x + 1y = 19 (I)
2x + 3y = 22 (II) onde x = partes usadas em sucos e y = partes usadas em refrescos;

somando I e II, temos
5x + 4Y =41(III)

resolvendo o sistema formado por (I) e (II)
3x + 1y = 19 (x2)
2x + 3y = 22 (x3)

-6x - 2y = -38
+6x + 9y = 66
-----------------
7y = 28
y = 28/7
y = 4 L

3x + y = 19
3x + 4 = 19
3x = 19 - 4 = 15
x = 15/3
x = 5 L
substituindo x e y em (III)

Sucos = (3+2).x = 5.5L = 25L
Refrescos = (1+3).y = 4.4L = 16L

Diferença:
Sucos - Refrescos= 25L - 16L = 9L

Alternativa (a)
UM JEITO SIMPLES E RÁPIDO:
SUCO = 3 PARTES DE CONCENTRADO E 2 DE ÁGUAREFRESCO = 1 PARTE DE CONCENTRADO E 3 DE ÁGUA(COM 19 LITROS DE CONCENTRADO E 22 LITROS DE ÁGUA) SUCO= 19/3+22/2=17,3 LITROS DE SUCOREFRESCO= 19/1+22/3= 26,3 LITROS DE REFRESCO - ELE PEDE A DIFERENÇA ENTRE OS DOIS:26,3 - 17,3 =9LETRA (A)
Suco: 3 partes de concentrado e duas de água
Refresco: 1 parte de concentrado e 3 de água

Suco: 19/3 + 22/2
38 + 66 = 104
104/6 = 17,3

Refresco: 19/1 + 22/3
57 + 22 = 79
79/3 = 26,3

26,3 - 17,3 = 9
Para fazer o suco ele utiliza uma proporção com três partes de concentrado e duas partes de água, ou seja, dividindo o suco em 5 partes (3 + 2), 3 partes são de concentrado e 2 partes são de água. Em outras palavras, em x litros de suco, 3/5 são de concentrado e 2/5 são de água.

Litros de suco = x
Litros de concentrado usados para fazer o suco = 3x/5
Litros de água usados para fazer o suco = 2x/5
Enquanto o “refresco” é obtido misturando uma parte de concentrado a três de água. Logo, dividindo o refresco em 4 partes (1 + 3), 1 parte é de concentrado e 3 partes são de água. Em outras palavras, em x litros de refresco, 1/4 é de concentrado e 3/4 são de água.

Total de litros de concentrado usados para fazer o suco e o refresco = 19 = 3x/5 + y/4
Total de litros de água usados para fazer o suco e o refresco = 22 = 2x/5 + 3y/4

Montando assim o sistema a baixo e resolvendo:

3x/5 + y/4 = 19 (1)
2x/5 + 3y/4 = 22 (2)

Isolando o "x" na equação (1):

3x/5 = 19 - y/4

3x = 5(19 - y/4)

3x = 95 - 5y/4

x = 95/3 - 5y/12 (3)

Substituindo "x" na equação (2):

2x/5 + 3y/4 = 22

(2/5)*(95/3 - 5y/12) + 3y/4 = 22

190/15 - 10y/60 + 3y/4 = 22

38/3 - y/6 + 3y/4 = 22

3y/4 - y/6 = 22 - 38/3

Tirando o MMC:

9y - 2y = 264 -152

7y = 112

y = 16

Substituindo "y" na equação (3), encontraremos o valor de "x":

x = 95/3 - 5y/12

x = 95/3 - 5*16/12

x = 95/3 - 80/12

x = 95/3 - 20/3

x = 75/3

x = 25

Logo, x - y = 25 - 16 = 9.

Resposta: Alternativa A.
Alguém poderia resolver esse outro, por favor?

Para higienizar uma salada, colocaram-se, em uma bacia, 3 litros de uma mistura de água sanitária e água,
na razão de 2 para 10. Como medida para o preparo da mistura, foram utilizados copos totalmente cheios
com capacidade de 1/4 de litro.
Assinale a alternativa que apresenta, corretamente, o número de copos totalmente cheios de água sanitária
que foram usados para o preparo dessa mistura.
Refresco = 1c + 3 a

19 de concentrado para fazer refresco: Não pode

10 c + 30a acabou a agua em 22a: não pode

5c + 15a ok mas sobra para Suco 14c + apenas 7 agua: não pode

Finalmente: 4c + 12a = y = 16 litros de Refresco. Sobra exatos 15a + 10a = x = 25 Litros suco

X-Y = 25-16 = 9 Litros

letra A
Guilherme Mendonça, penso que vc inverteu a ordem das palavras "água" e "água sanitária" na pergunta, por isso, suponho que seja 2/10

Onde a cada 2 partes de água sanitária há 10 de água

1 copo = 1/4 L (dividi 1 litro em 4 partes e cada parte vale 1 copo), logo, 1 L = 4 copos

Então, em 3 L = 12 copos

Sendo a proporção 2/10, significa que são 2 copos de água sanitária + 10 copos de água, ou o contrário se a pergunta é realmente como vc fez.

ID

946138

Banca

VUNESP

Órgão

FUNDUNESP

Ano

2013

Provas

VUNESP - 2013 - FUNDUNESP - Engenheiro de Segurança

Disciplina

Matemática

Assuntos

No último dia de aula, foi preparada uma apresentação de teatro só para alunos de uma escola. O número de alunos da escola era 3 vezes maior do que o número total de assentos do auditório onde ocorreria a apresentação. Então, para que todos os alunos assistissem à peça, eles foram divididos em 5 grupos de mesmo número. Sabendo-se que todos os alunos da escola assistiram à apresentação uma única vez e que em cada apresentação 64 assentos do auditório ficaram vazios, a diferença entre o número de alunos da escola e o número de assentos desse auditório é

Alternativas

320.

264.

208.

152.

96.

Comentários

x= número de alunos;
y= número de assentos;
O número de alunos da escola era 3 vezes maior do que o número total de assentos do auditório onde ocorreria a apresentação;
x=3y(I)
para que todos os alunos assistissem à peça, eles foram divididos em 5 grupos de mesmo número. todos os alunos assistiram à apresentação uma única vez e que em cada apresentação 64 assentos ficaram vazios;
x/5=y-64(II);
substituindo (I) em (II) temos.
3y/5=y-64 multiplicando ambos os termos por 5 temos;
5*(3y/5)=5*(y-64)
3y = 5y-320
3y-5y=-320
-2y=-320(-1)
2y=320
y=160
substituindo em (I)
x= 3*160
x=480
x-y= 480-160=320
Alternativa A
A = Alunos
L = Lugares

A = 3L
A/5 = L/5 + 64 (aqui é "+", pois os lugares sobraram depois de ser divido pelos 5 grupo. Sobraram "a mais", e não "a menos" - o que seria "faltar lugar")

3L/5 = L/5+ 64
3L = 5(L/5+ 64)
3L = 5L/5 + 320
3L = L + 320
L = 160

A = 3L = 480
A - L = 480 - 160 = 320
L = lugares
nº alunos:
NA = 3 * lugares

foram divididos em 5 grupos de mesmo número:
NA/5

diferença entre os lugares vazio e os alunos divididos em 5 gupos:
L - NA/5 = 64
L - (3 * L/5) =64

usando o mmc:
(5L - 3L)/5 =64
2L = 64*5
L = 320/2
L = 160 lugares

NA = 3 * 160
NA = 480 alunos

diferença entre o número de alunos da escola e o número de lugares desse auditório é:
480 - 160 = 320 lugares
A = alunos
C = cadeiras do auditório

A = 3C
A/5 = C - 64
pergunta do problema: A - C = ?

A/5 = C - 64
A = 5 . (C - 64)
A = 5C - 320
5C - 320 = 3C
5C - 3C = 320
2C = 320
C = 320/2
C = 160

A = 3C
A = 3 . 160
A = 480

480 - 160 = 320

Gab A

ID

951265

Banca

EXATUS

Órgão

DETRAN-RJ

Ano

2012

Provas

EXATUS - 2012 - DETRAN-RJ - Todos os Cargos - Conhecimentos Gerais

Disciplina

Matemática

Assuntos

Numa lanchonete, compra-se 2 sucos e 3 lanches por R$ 21,10. Se o cliente preferir 3 sucos e 2 lanches, pagará R$ 18,40. O valor cobrado pelo suco nessa lanchonete é:

Alternativas

R$ 2,50.

R$ 2,60.

R$ 2,70.

R$ 2,75.

Comentários

s=sucos; l= lanches; *=multiplicação
2s+3l=21,1 (I)
3s+2l=18,40 (II)
Temos um sistema de equaçoes. Podemos multiplica (I) por (-2) e (II) por (3);

[2s+3l=21,1]*(-2)
[3s+2l=18,40]*(3)

-4s - 6l = -42,2
9s +6l = 55,2
------------------
5s = 13
s=2,6. isto é R$ 2,60
Alternativa B
b) R$ 2,60.
Numa lanchonete, compra-se 2 sucos e 3 lanches por R$ 21,10 (considerando sucos = x & lanches= y, temos 2x+3y=21.10). Se o cliente preferir 3 sucos e 2 lanches, pagará R$ 18,40 (3x+2y=18.40). suco (x) =

Sistemas

2x+3y=2110
3x+2y=1840

2x=2110-3y
x=2110-3y/2

3(2110-3y)/2+2y=1840
6330-9y/2+2y=1840

6330-5y/2=1840
6330-5y=3680
-5y=-2650
y=530

2x+3(530)=2110
2x+1590=2110
2x=520
x=160

Suc= 1,60$
Suco = X Lanche = Y
2X+3Y = 21,10 * (-2)
3X+2Y = 18,40 * (3)
-4X - 6Y = -42,20
9X + 6Y = 55,20
Subtraindo as equações e simplificando os números em azul, temos:
5X = 13
X = 2,6 (Suco)
Só não entendi o por que do o (-2) e o 3 como chegou a essa conclusão
X=Sucos e Y=Lanches
2x+3Y=21,10 * (-3) >>> -6x - 9y = -63,30 >>> - 5y = - 26,50 * (-1) >>> y = 26,50/ 5 >>> y = 5,30 (custo do lanche)
3x+2y=18,40 *(2) 6x + 4y = 36,80
(agora escolha qualquer equação acima e substitua o "y" por 5,30)
2x + 3 * 5,30 = 21,10 >>> 2x = 21,10 - 15,90 >>> 2x = 5,20 >>> x = 5,20/ 2 >>> x = 2,60 (custo do suco)
Resposta: Alternativa B

ID

990685

Banca

Makiyama

Órgão

CPTM

Ano

2012

Provas

Disciplina

Matemática

Assuntos

Paula e Vítor foram os ganhadores de um bolão entre os alunos da sua classe.Sabe-se que ambos receberam valores distintos em Reais.Sabemos ainda que caso Paula empreste R$ 20,00 para Vítor, ambos ficarão com quantias iguais; caso Vítor empreste R$ 20,00 para Paula, esta ficará com o triplo do que restará para Vítor.Portanto,podemos afirmar que o valor total dos prêmios recebidos por Paula e Vítor é de:

Alternativas

R$ 100,00

R$ 120,00

R$ 140,00

R$ 160,00

R$ 180,00

Comentários

P - 20 = V + 20 = P - V = 40 (I)

3*(V- 20) = P+20 = - P + 3 V = 80(II)
I E II FORMAM UM SISTEMA
P - V = 40
-P + 3 V = 80
2 V = 120

V = 120/2
V = 60
SUBSTITUINDO EM I
P - 60 = 40
P=40+60
P = 100
T = 100 + 60 = R$ 160,00
ALTERNATIVA D
P - 20 = V + 20 = P - V = 40 (I)

3*(V- 20) = P+20 = - P + 3 V = 80(II)
I E II FORMAM UM SISTEMA
P - V = 40
-P + 3 V = 80
2 V = 120

V = 120/2
V = 60
SUBSTITUINDO EM I
P - 60 = 40
P=40+60
P = 100
T = 100 + 60 = R$ 160,00
ALTERNATIVA D
PAULA = 100

VITOR = 60

TIRO 20 DE PAULA E DOU PARA VITOR
PAULA = 100 - 20 = 80
VITOR = 60 + 20 = 80
OS DOIS ESTÃO COM OS MESMOS VALORES. AGORA FAÇO O CONTRÁRIO, TIRO 20 DE VITOR E DOU PARA PAULA
PAULA = 100 + 20 = 120
VITOR = 60 - 20 = 40
OU SEJA, PAULA TEM O TRIPLO QUE VITOR (40 X 3 = 120)

ID

990697

Banca

Makiyama

Órgão

CPTM

Ano

2012

Provas

Disciplina

Matemática

Assuntos

Pensando em comprar um brinquedo, Pedrinho resolveu guardar em um “cofre” apenas moedas de 50 e 25 centavos. Hoje, Pedrinho abriu o “cofre” e encontrou um total de 100 moedas.Dado que a quantia existente no “cofre” é maior que R$ 33,00 e menor que R$ 35,00; pode-se afirmar que a quantidade x de moedas de 50 centavos é:

Alternativas

25 < x < 28

28 < x < 30

45 < x < 50

32 < x < 40

40 < x < 45

Comentários

>33 e <35

32*0,50 = 16

68*0,25 = 17

Então: 16 + 17 = 33

40*0,5 = 20

60*0.25 = 15

Então: 20+15= 35

obs: a letra d atende os dois limites.
d) 32 < x < 40

Pensando em comprar um brinquedo, Pedrinho resolveu guardar em um “cofre” apenas moedas de 50 e 25 centavos (adotemos x && y para moedas de 50 && 25; x=50c // y=25c). Hoje, Pedrinho abriu o “cofre” e encontrou um total de 100 moedas (somando as de 50 e as de 25==100. Logo, x+y=100). Dado que a quantia existente no “cofre” é maior que R$ 33,00 e menor que R$ 35,00 (façamos o calculo 2 vezes; 1 com equacao = 33 && outra com =35) ; pode-se afirmar que a quantidade x de moedas de 50 centavos é:

x+y=100
50x+25y>3500

isolamos y para substituir na inequacao.

||y=100-x||

50x+25*(100-x)<3500
50x+2500-25x<3500
25x<1000
x<40

50x+25*(100-x)>3300
50x+2500-25x>3300
25x>800
x>32

x>32 && x<40.

obs.:para facilitar, convertem-se as medidas monetarias para a mesma medida. neste caso, os reais foram convertidos para cents.
Creio que essa questão não seja necessário fazer conta alguma, pois vejamos, o valor total do cofrinho de Pedrinho é X, sabendo que X é maior que 33 e menor que 35, logo, se X é menor de 35, ja eliminamos a resposta E, C. Pois não pode ser maior que 40 e nem maior que 45

E "X" é maior que 33, logo elinimanos A e B, Pois o enunciado ja mostra que o valor tente a ser entre 33 e 45, e a letra A e B são valores diferentes destes. Sobrando a resposta mais lógica, letra D

Foi assim que pensei pra resolver a questão.
Maria, ele não quer saber o valor que ele tinha no cofre. O enunciado pergunta a quantidade de moedas de 50 centavos, que ao meu ver sua explanação não tem lógica nenhuma. Foi pura coicidencia com a resposta.

ID

993652

Banca

Makiyama

Órgão

CPTM

Ano

2011

Provas

Makiyama - 2011 - CPTM - Médico do trabalho

Disciplina

Matemática

Assuntos

Sabe-se que o produto da idade de Miguel pela idade de Lucas é 500. Miguel é 5 anos mais velho que Lucas. Qual a soma das idades de Miguel e Lucas?

Alternativas

40.

55.

65.

50.

45.

Comentários

e) 45.

Sabe-se que o produto da idade de Miguel pela idade de Lucas é 500 (L*M=500). Miguel é 5 anos mais velho que Lucas (M=L+5). Qual a soma das idades de Miguel e Lucas (M+L=??)?

L*M=500
M=L+5

L*(L+5)=500

L²+5L-500=0

Bascara:

x=(-5+-V-5²-4*1*-500)/2

x=(-5+-V(25+2000))/2

x=(-5+-V2025)/2

x=(-5+-45)/2

x'=(-5+45)/2

x'=40/2=20

x"=(-5-45)/2

x"-25 (é uma raiz da funcao, mas nao se aplica no problema)

L=20

M=L+5

M=25

M+L=25+20==45

ID

1009222

Banca

Makiyama

Órgão

CPTM

Ano

2012

Provas

Makiyama - 2012 - CPTM - Técnico - Licitações

Disciplina

Matemática

Assuntos

Paula e Vítor foram os ganhadores de um bolão entre os alunos da sua classe. Sabe-se que ambos receberam valores distintos em Reais. Sabemos ainda que caso Paula empreste R$ 20,00 para Vítor, ambos ficarão com quantias iguais; caso Vítor empreste R$ 20,00 para Paula, esta ficará com o triplo do que restará para Vítor. Portanto, podemos afirmar que o valor total dos prêmios recebidos por Paula e Vítor é de:

Alternativas

R$ 100,00

R$ 120,00

R$ 140,00

R$ 160,00

R$ 180,00

Comentários

Paula e Vitor

Se PAULA emprestar 20 para VITOR, ficará com a mesma quantia, logo:

P = V+20

Mas se VITOR emprestar 20 para PAULA, PAULA terá 3 x a quantia de VITOR

P+20=3V

Daí eu coloquei os valores

(V+20)+20=3V

V+20+20=3V

40=3V-V

40=2V

V=20

Logo P = 20+20 = 40

Se somarmos os valores de P e V chegamos a 60, mas não temos essa alternativa. No entanto eu marquei 160 e acertei, não sei se foi coincidência matemática, mas penso que seria 100% do valor total. Por isso 160. Se alguem tiver uma explicação melhor por favor :)
P-20 = V+20 -> empréstimo de Paula para Vitor (Equação 1)
P+20 = 3(V-20) -> empréstimo de Vitor para Paula
P+20 = 3V-60
P = 3V-80 (Equação 2)
Voltando à equação - e substituindo os valores:
(3V-80)-20 = V+20 (Equação 1)
3V-100 = V+20
2V = 120
V= 60
P= 3*60-80 (Equação 2)
P=100
Somando os dois valores (de Paula e Vitor) obtemos o resultado 160, questão "D"!

ID

1009225

Banca

Makiyama

Órgão

CPTM

Ano

2012

Provas

Makiyama - 2012 - CPTM - Técnico - Licitações

Disciplina

Matemática

Assuntos

No Parque da Cidade, a barraca da tia Maria aluga apenas bicicletas e triciclos.
A quantidade total desses veículos é 50 e o número de rodas é de 120. Assim, podemos afirmar que a barraca da tia Maria possui:

Alternativas

30 bicicletas e 20 triciclos

10 bicicletas e 40 triciclos

32 bicicletas e 18 triciclos

28 bicicletas e 32 triciclos

20 bicicletas e 30 triciclos

Comentários

Só montar o sisteminha
B + T = 50

2B+3T=120

B=50-T

2(50-T)+3T=120

100-2T+3T=120

T=20

B=50-T = 30
B+ T= 50 (.-2) multiplica por -2

2B+3T= 120

-------------------

-2B-2T= -100

2B+3T=120

--------------------------

T= 20 Substitui os valores onde B+T= 50 ---> Se T vale 20<=> B=30
para economizar tempo é só fazer o numero de bicicletas da alternativa vezes 2(numero de rodas) e o numero de triciclos por 3(numero de rodas), se bater 120 os dois juntos na mesma alternativa é a questão correta.

ID

1012693

Banca

FUNDATEC

Órgão

CRA-RS

Ano

2010

Provas

FUNDATEC - 2010 - CRA-RS - Técnico em Informática

Disciplina

Matemática

Assuntos

Uma menina possui 5 blusas, 3 saias e 2 sandálias. De quantas maneiras diferentes ela pode se vestir?

Alternativas

Comentários

Pensei o seguinte:
Blusa 1 - Saia 1 - Sandália 1
- Sandália 2
- Saia 2 - Sandália 1
- Sandália 2
- Saia 3 - Sandália 1
- Sandália 2
Dessa forma, eu posso fazer 6 combinações diferentes:
B1 - S1 - SD1
B1 - S1 - SD2
B1 - S2 - SD1
B1 - S2 - SD2
B1 - S3 - SD1
B1 - S3 - SD2
Assim, para contabilizar as 5 blusas, devo multiplicar as possibilidades encontradas com a blusa 1 (6) pelo número de blusas (5).
6x5= 30
Resolvi por combinação. A demonstração apresentada anteriormente nada mais é do que a visualização das combinações possíveis.
C5,1 x C3,1 x C2,1 = 30
Tenho 5 opções de blusas e desejo escolher uma.
Tenho 3 opções de saias e desejo escolher uma.
Tenho 2 opções de sandálias e desejo escolher uma.
Para formar o conjunto eu preciso usar uma blusa, uma saia e uma sandália. Devido a conjunção "e" ocorre a multiplicação. Se fosse "ou" seria uma soma.
5 blusas x 3 saias x 2 sandálias = 30
LETRA: A
Pegue o menor e ligue até o maior, passando pelo meio.

Mas de não quiser desenhar para não parecer feio (meio tipo assim: 1ª série), então basta multiplicar: 2*3=6*5=30 ou, ainda, 5*3=15*2=30 (BINGO!!!)

ID

1013152

Banca

CESPE / CEBRASPE

Órgão

UNB

Ano

2013

Provas

CESPE - 2013 - UNB - Vestibular - Prova 2

Disciplina

Matemática

Assuntos

Quatro amigos, Raul, Pedro, João e Tiago, contribuíram com um total de R$ 50.000 para cobrir as despesas de suas famílias durante as férias. A contribuição de Raul adicionada ao dobro da contribuição de Pedro foi igual à contribuição de Tiago adicionada ao triplo da contribuição de João. Cada um deles contribuiu com um valor superior a R$ 5.000.

A soma das contribuições de Raul e Pedro não pode ter sido igual à soma das contribuições de Tiago e João.

Alternativas

Certo

Errado

Comentários

Errado.
A contribuição de Raul adicionada ao dobro da contribuição de Pedro FOI IGUAL à contribuição de Tiago adicionada ao triplo da contribuição de João. Cada um deles contribuiu com um valor superior a R$ 5.000.
R + 2P = 25000
T + 3J = 25000
Não entendi como deduziu que as somas dão 25mil.
Sejam x, y, z e t as respectivas contribuições de Raul, Pedro, João e Tiago, respectivamente. Como a contribuição total foi de R$ 50.000 temos uma primeira equação:

x + y + z + t= 50.000 (i)

Ainda do enunciado, podemos montar uma segunda equação:

x+ 2y= t+ 3z (ii)

Consideramos a possibilidade de

x + y = t + z (iii)

De (iii):

x = t + z – y

Substituindo (iii) em (ii)

t + z – y + 2 y = t + 3 z ⇔ y = 2z

Substituindo (iii) em (i):

t + z + z + t = 50.000 ⇔ t = 25.000 – z

Se montarmos um sistema com as equações i, ii e iii, veremos que seria um sistema indeterminado, cuja solução será da forma (x, y, z, t) = (25.000 – 2z, 2z, z, 25.000 – z).

Como o enunciado nos diz que a contribuição de cada um é maio do que 5 mil reais, podemos fazer um exemplo de distribuição atribuindo o valor de z = 6000 mil como exemplo, assim:

(x, y, z, t) = (13000, 12000, 6000, 19000)

Logo a soma das contribuições de Raul e Pedro pode ter sido igual à soma das contribuições de Tiago e João.

Errado.

ID

1013155

Banca

CESPE / CEBRASPE

Órgão

UNB

Ano

2013

Provas

CESPE - 2013 - UNB - Vestibular - Prova 2

Disciplina

Matemática

Assuntos

Raul pode ter contribuído com R$ 16.000; Pedro, com R$ 10.000; João, com R$ 12.000; e Tiago, com R$ 12.000.

Alternativas

Certo

Errado

Comentários

R + 2P = 25000        16+20= 26
T + 3J = 25000         12+36= 48
                                            74
Errado.
Sejam x, y, z e t as respectivas contribuições de Raul, Pedro, João e Tiago, respectivamente. Como a contribuição total foi de R$ 50.000 temos uma primeira equação:

x + y + z + t= 50.000 (i)

Ainda do enunciado, podemos montar uma segunda equação:

x+ 2y= t+ 3z (ii)

Assim, utilizando a equação II e substituindo: x =16000, y = 10000 e t = 12000:

16000+2*10000 = 12000+3*12000 → 36000 ≠ 48000

Errado.
Só corrigindo Daniel, 16000 + 20000 = 36000
12000+ 36000 = 48000

Partindo-se da fórmula R+2P = T+3J

Que Deus ilumine nossos sonhos

ID

1013158

Banca

CESPE / CEBRASPE

Órgão

UNB

Ano

2013

Provas

CESPE - 2013 - UNB - Vestibular - Prova 2

Disciplina

Matemática

Assuntos

Raul pode ter contribuído com R$ 16.000, e Tiago, com R$ 8.000.

Alternativas

Certo

Errado

Comentários

ué, no enunciado diz que R + 2P=T + 3J. ou seja, R+2P=25 e T+3J=25

se Raul contribuiu com 16, temos: 16 + 2P=25 => 2P=9 => P=4,5

NO enunciado também diz que CADA UM CONTRIBUIU COM MAIS DE 5

logo, Raul não pode ter contribuido com 16, pois assim, Pedro não teria contribuído com mais de 5.

Questão errada....

Tô certo?? Se estiver errado, me corrijam por favor!
Sejam x, y, z e t as respectivas contribuições de Raul, Pedro, João e Tiago, respectivamente. Como a contribuição total foi de R$ 50.000 temos uma primeira equação:

x + y + z + t= 50.000 (i)

Ainda do enunciado, podemos montar uma segunda equação:

x+ 2y= t+ 3z (ii)

Assim:

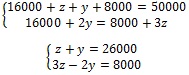
Logo, z = 12000 e y = 14000.

Certo.
É simples. Vejam só...
16.000 + 8.000 = 24.000, concordam?
Se na questão diz que R+2P (24.000) é igual a T+3J, logo entende-se que T+3J também tem que ser igual a 24.000
Ora, se a soma total da contribuição foi de 50.000, como podemos afirmar que as duplas contribuíram com 24.000 cada uma se a soma destas é 48.000?
Espero ter ajudado.
Concordo com a banca questão certa...
SE o total e 50 mil
raul + 2 x pedro = tiago + 3 x joão ... o valor que raul e pedro contribuiram tem k ser o mesmo valor de tiago e joão... portanto 25 mil
... raul = 16.000 , tiago 8.000
16.000 + 2 x pedro = 8.000 + 3 x joão... o valor que pedro colocou foi 2 x 4,500 = 9 mil e joão 3 x 5666,66 = 17 mil
portanto todos investiram mais que 5 mil ... raul 16 mil + pedro 9 mil + tiago 8 mil + joão 17 mil.... abraço a todos
R+P+J+T=50.000
R + 2P = T + 3J
SE A CONTRIBUIÇÃO DE RAUL E PAULO FOI IGUAL A CONTRIBUIÇÃO DE TIAGO E JOÃO ENTÃO:
R+2P=25.000
T+3J=25.000

R+2P=25.000
16.000 + 2P=25.000
16.000 P/ CHEGAR A 25.000 FALTAM 9.000 DE PAULO, QUE SERIA NA VERDADE 4.500 MAS COMO PAULO É O DOBRO FICA 9.000;

T + 3J=25.000
SE DO TIAGO FOI 8.000 PARA CHEGAR A 25.000 JOÃO TERIA QUE CONTRIBUIR COM 17.000, QUE É O TRIPLO DE 5666,66.
Ficando assim a contribuição:
R=16
P=9
T=8
J=17
QUESTÃO CORRETA: CADA UM CONTRIBUIU COM MAIS DE 5.000.
Acertei essa questão fazendo da seguinte forma:
R= Raul
P= Pedro
J= João
T = Tiago
R+P+J+T=50.000 (I)
R + 2P = T + 3J (II)
R > 5.000,00
P > 5.000,00
J > 5.000,00
T > 5.000,00
Condição:
R = 16.000,00
T = 8.000,00
Reescrevendo (II), temos que:
R + 2P = T + 3J
2P = T + 3J - R
2P = 8.000,00 + 3J - 16.000,00
2P = 3J - 8.000,00
P = (3J - 8.000,00)/2
Reescrevendo (I), temos que:
R+P+J+T=50.000
16.000,00 + ((3J - 8.000,00)/2) + J + 8.000,00 = 50.000,00
24.000,00 + ((3J - 8.000,00)/2) + J = 50.000,00
((3J - 8.000,00)/2) + J = 50.000,00 - 24.000,00
(3J)/2) + J = 50.000,00 - 24.000,00 + 4.000,00
Obs: o 4.000,00 do cálculo acima apareceu porque dividi por dois o valor de 8.000,00 que estava do outro lado da igualdade
2.5J = 30.000,00
J = 12.000,00
Reescrevendo (I), temos que:
R+P+J+T=50.000
16.000,00 + P + 12.000,00 + 8.000,00 = 50.000,00
P = 50.000,00 - 16.000,00 - 12.000,00 - 8.000,0
P = 14.000,00
Verificando a validade do cálculo:
1) R + 2P = T + 3J
16.000,00 + 2*14.000,00 = 8.000,00 + 3*12.000,00
16.000,00 + 28.000,00 = 8.000,00 + 36.000,00
44.000,00 = 44.000,00
Resposta: Correto
2) R > 5.000,00 ; P > 5.000,00; J > 5.000,00 ; T > 5.000,00
R = 16.000,00
P = 14.000,00
J = 12.000,00
T = 8.000,00
Resposta: correta
Primeiramente:
R + 2P = T + 3J
R+P+T+J = 50.000
------------------------------------
R=16.000
T=8.0000
------------------------------------
16000 + 2P = 8000 + 3J
--> 3J - 2P = 16000 - 8000
--> 3J - 2P = 8000
------------------------------------
Trocando os valores de:
R+P+T+J = 50.000
16000+P+8000+J = 50000
P+J = 50000-24000
--> P+J = 26000
------------------------------------
Agora é só igualar alguns deles, vamos multiplicar por 2:
2P + 2J = 52000
(+) 3J - 2P = 8000
Logo: 5J = 60000
J = 12.000
------------------------------------
R = 16.000
T = 8.0000
J = 12.000
P = 14.000
É só tirar a prova real!
(R=16000) + (2P=28000) = (T=8000) + (3J=36000)
44000 = 44000

Gabarito: Correto.
Eu fui pela lógica. O enunciado perguntou se seria possível eles terem contribuido com esse número.

Basta colocar o valor mínimo na fórmula e ver se não estrapola os 50000. Foi o que eu fiz :)

ID

1013164

Banca

CESPE / CEBRASPE

Órgão

UNB

Ano

2013

Provas

CESPE - 2013 - UNB - Vestibular - Prova 2

Disciplina

Matemática

Assuntos

Se Tiago contribuiu com R$ 10.000 e a soma da contribuição de Raul com o dobro da contribuição de João foi igual a R$ 32.000, então, a contribuição de João, em reais, foi

Alternativas

inferior a 10.500.

superior a 10.500 e inferior a 12.000.

superior a 12.000 e inferior a 13.500.

superior a 13.500.

Comentários

Seja as equações
R + P + J + T = 50.000 (I) e R + 2P = T + 3J (II)

Fazendo T = 10000 e R = 32000 - 2J, teremos o sistema linear abaixo:

Logo:

Assim temos q J = 38000/3 o que dá aproximadamente 12666

Letra C

ID

1023868

Banca

PUC - RS

Órgão

PUC - RS

Ano

2011

Provas

PUC - RS - 2011 - PUC - RS - Vestibular - Prova 2

Disciplina

Matemática

Assuntos

Procurando resolver um desafio proposto em certa disciplina do curso de Nutrição, uma estudante foi à Biblioteca e encontrou em um livro o seguinte problema:

Uma dieta requer, para a refeição principal, 7 unidades de gordura, 9 unidades de proteínas e 16 unidades de carboidratos. Certa pessoa dispõe de 3 alimentos com os quais pode montar sua dieta.

Alimento A: cada medida contém 2 unidades de gordura, 2 unidades de proteína e 4 unidades de carboidrato.

Alimento B: cada medida contém 3 unidades de gordura, 1 unidade de proteína e 2 unidades de carboidrato.

Alimento C: cada medida contém 1 unidade de gordura, 3 unidades de proteína e 5 unidades de carboidrato.

O número de medidas que a pessoa consome dos alimentos A, B e C em sua refeição principal é representado por x, y, z, respectivamente. O sistema linear cuja solução diz quantas medidas de cada alimento deve ser consumido é _________.

A estudante levou o problema para resolver com seu grupo, que chegou à seguinte resposta correta:

Alternativas

Comentários

alguem faz por favor
Primeiro vc vai fazer a junção de todas as gorduras, proteínas e carboidratos:
GORDURAS: Alimento A: 2 unidades;
Alimento B: 3 unidades; = 7 unidades de gordura
Alimento C: 1 unidade;

PROTEÍNAS: Alimento A: 2 unidades;
Alimento B: 1 unidade; = 9 unidades de proteínas
Alimento C: 3 unidades;

CARBOIDRATOS: Alimento A: 4 unidades;
Alimento B: 2 unidades; = 16 unidades de carboidratos
Alimento C: 5 unidades;

Logo, a montagem do sistema linear é feito para que as medidas dos alimentos sejam determinadas pelos seus consumos:
2x + 3y + z = 7
2x + y + 3z = 9
4x + 2y + 5z = 16
Desta forma, a resposta correta é a letra C.

ID

1032358

Banca

CRS - PMMG

Órgão

PM-MG

Ano

2013

Provas

CRS - PMMG - 2013 - PM-MG - Soldado da Polícia Militar

Disciplina

Matemática

Assuntos

Marque a alternativa CORRETA. Em um estacionamento existe um total de 50 vagas para carros pequenos e motocicletas. Quando este estacionamento está completamente lotado, a quantidade de rodas de veículos é igual a 120. Os números de vagas para carros e motos são, respectivamente:

Alternativas

10 e 40

20 e 30

25 e 25

15 e 35

Comentários

Olá amigos do QC, M = motos( 2 rodas) e C = carro( 4 rodas).

Quando as vagas estiverem completas = M + C = 50
                                                                          2.M + 4C = 120
estamos diante de um sistema com duas equações e duas variáveis, pelo método da soma multiplicamos a primeira equação por - 2:

    - 2. M - 2.C = - 100
      2. M + 4.C = 120
--------------------------------
                2.C = 20
                   C = 20/2
                   C = 10
M + C = 50
M + 10 = 50
M = 50 - 10
M = 40

Então 10 carros e 40 motos.

Grande abraço e Deus é bom.
vo chamar C de carro e M de moto e como cada carro tem 4 rodas e cada moto tem duas rodas, podemos fazer da seguinte forma:

c+m=50----------------------c=50-m substituir esse valor na equação de baixo e assim temos:
4c+2m=120

4(50-m)+2m=120
200-4m+2m=120
-2m=-200+120
m=80/2
m=40 sendo assim colocamos este valor na equação de cima

c=m=50
c+40=50
c=50-40
c=10 assim sendo temos 10 carros e 40 motos
A paz de Cristo futuros policiais.
Este é simples também.
Solução.
quantidade de carros = x
quantidade de motos = y
total de rodas de carros = 4x
total de rodas de motos = 2y

montado o sistema temos: x+y = 50
4x+2y=120
multiplicando a primeira equação por -2, conseguiremos anular uma variáve e passaremos a ter o seguinte:

-2x-2y=-100
4x+2y=120 2x =20, x= 10, então concluímos que o número de carros é igual a 10 e, por exclusão, o de motos será de 40
Resolvi esta questão testando as respostas:

10 carros = 40 rodas
40 motos = 80 rodas

total de rodas = 120

Para quem não sabe por onde começar, vai a dica.
Fiz como a Glaucia, resolvi a partir das alternativas.
E exitem inúmeros métodos, para resolver este problema:
x=carros
y=motos

x+y=50
4x+ 2y=120 ( o carro tem 4 rodas e a moto tem 2 rodas)

x= 50-y *****

4(50-y) + 2y=120
200-4y +2y=120
-2y= 120-200
2y= 80
y=40

x= 50-40=10
Montando um sistema onde "x" é o número de carros e "y" o número de motocicletas, temos:

|x + y = 50
|4x + 2y = 120 (4x pois cada carro possui 4 rodas e 2y pois cada motocicleta possui 2 rodas)

Multiplicando por -2 a primeira equação do sistema acima, e depois somando ambas equações:

|-2x - 2y = -100
| 4x + 2y = 120

2x = 20
x = 10

Assim, substituindo-se "x" em qualquer uma das equações do sistema, encontraremos y = 40. Logo, os números de vagas para carros e motos são, respectivamente: 10 e 40.

Resposta: Alternativa A.
Montando um sistema onde "x" é o número de carros e "y" o número de motocicletas, temos:

|x + y = 50
|4x + 2y = 120 (4x pois cada carro possui 4 rodas e 2y pois cada motocicleta possui 2 rodas)

Multiplicando por -2 a primeira equação do sistema acima, e depois somando ambas equações:

|-2x - 2y = -100
| 4x + 2y = 120

2x = 20
x = 10

Assim, substituindo-se "x" em qualquer uma das equações do sistema, encontraremos y = 40. Logo, os números de vagas para carros e motos são, respectivamente: 10 e 40.

ID

1037029

Banca

MS CONCURSOS

Órgão

Prefeitura de São Paulo - SP

Ano

2011

Provas

MS CONCURSOS - 2011 - Prefeitura de São Paulo - SP - Guarda Civil Metropolitano

Disciplina

Matemática

Assuntos

A soma entre dois números positivos é 37. Se o produto entre eles é 330, então o valor da di ferença entre o maior e o menor número é:

Alternativas

23.

61.

17.

49.

Comentários

Soma -> 22 + 15 = 37
Produto -> 22 . 15 = 330
22-15 = 7
fazer sistema:

x+y = 37 => y = 37-x

x.y = 330 => x.(37-x)= 330 . Assim, tem -se uma equação do 2o grau, cujas raízes são 22 e 15
faz bascara e acha o X1 e X2 e a diferença entre eles é o resultado
Complementando o comentário da Márcia.

x.(37-x)= 330
37x - x² = 330
x² - 37x + 330
a = 1
b = - 37
c = 330

-(b) +ou- √(b)² - 4 . a . c / 2 . a
-(-37) +ou- √ (-37)² - 4 . 1 . (330) / 2 . 1
37 +ou- √ 1369 - 1320 / 2
37 +ou- √ 49 / 2
37 +ou- 7 / 2

37 + 7 / 2 = 44/2 = 22
37 - 2 / 2 = 30/2 = 15

ID

1053043

Banca

FCC

Órgão

TRT - 15ª Região (SP)

Ano

2013

Provas

Disciplina

Matemática

Assuntos

Certo número de cestas básicas foram compradas para distribuir para alguns funcionários de uma empresa, sendo que cada funcionário que recebe a cesta receberá uma única cesta. Se as cestas fossem distribuídas para todos os funcionários do setor A, sobrariam 12 cestas. Se elas fossem distribuídas para todos os funcionários do setor B, faltariam 8 cestas. Se fossem distribuídas para todos os funcionários do setor C, não faltariam nem sobrariam cestas básicas. Nas circunstâncias descritas, o total de funcionários dos setores A, B e C dessa empresa, juntos, é igual ao

Alternativas

triplo do número de cestas básicas compradas, menos 4.

triplo do número de cestas básicas compradas, mais 4.

número de cestas básicas compradas, menos 4.

número de cestas básicas compradas, mais 4.

dobro do número de cestas básicas compradas, mais 20.

Comentários

tx= total de cestas
x=cestas
A= tx-12x sobrou
B= tx+8x faltou
C= tx
somando A+B+C= 3tx-4x
triplo do numero total de cestas menos 4
Supondo que X = número de cestas básicas.
X - A = 12
X - B = -8
X - C = 0
Supondo, ainda, que X = 20 (escolhi livremente):
20 - 8 = 12 (A tem que ser 8)
20 - 28 = -8 (B teria que ser 28)
20 - 20 = 0 (C = 20)
Logo, testando a primeira alternativa: A + B + C = 8 + 28 + 20 = 56 (total de funcionários). E 3 x 20 = 60.
60 - 4 = 56.
Ainda bem que era a primeira alternativa... economia de tempo. hehe
http://professorlg.com/2014/01/25/trt-15a-regiao-questao-15/
Mais simples ...
x= número de cestas básicas compradas.

· x= a +12, logo: a= x-12;

· x= b – 8, logo: b=x+8;

· x= c;

Pedido da questão: a+b+c=?

a+b+c= (x-12) + ( x +8 ) + (x) = 3x – 4
"triplo do número de cestas básicas compradas, menos 4".
Logo, alternativa A.
Esse raciocínio/comentário aí do Haroldo achei interessante.
Eu mantenho p/ mim mesmo outras contas que fiz aprofundando o "problema" (questão),
sendo que ainda não cheguei a elaborar gráfico dos valores válidos p/ as variáveis.
NÃO QUE ESSE APROFUNDAMENTO SEJA RELEVANTE QTº AO QUE É AÍ COBRADO,
nem mesmo o gráfico.
Galera, a resolução dessa questão é:
Se distribuidas as cestas para A - sobraria, então seria ->                     X -12 = A
Se distribuidas as cestas para B - faltaria, então seria ->                      X+  8 = B
Se distribuidas as cestas para C não faltaria e nem sobraria, então     X + 0   = C
a SOMA SERIA ENTÃO:                                                                        3X - 4 = A + B +C
Resposta: letra A
Se tiverem dúvidas, por gentileza, entrar nesse link q tem a resolução da questão em vídeo: http://www.youtube.com/watch?v=gL3PzT6lmTo
Abs...
x cestas= 100 (para o cálculo ficar mais fácil)
então o :
setor A= 88 (funcionários) sobrou 12
setor B= 108 (funcinários) faltou 8
setor C= 100 (funcionários) não sobrou e não faltou
total func = A+B+C => 88+108+100=296
o triplo de cestas compradas (100x3) - 4 (resposta A)
Achei o resultado de uma maneira mais fácil.
O problema diz: Certo número de cestas básicas foram compradas para distribuir para alguns funcionários de uma empresa, sendo que cada funcionário que recebe a cesta receberá uma única cesta. Se as cestas fossem distribuídas para todos os funcionários do setor A, sobrariam 12 cestas. Se elas fossem distribuídas para todos os funcionários do setor B, faltariam 8 cestas. Se fossem distribuídas para todos os funcionários do setor C, não faltariam nem sobrariam cestas básicas. Dadas as circunstâncias, no setor C temos: 12 FUNCIONÁRIOS; no setor B: 12+8=20 FUNCIONÁRIOS; setor A= 0.
Sendo assim: 12+20+0=32
Triplo de cestas: 12x3=36 / 36-4=32 (nº de funcionários)
Resposta: A
Não entendi é foi nada!
sendo x o numero de cestas:
a+12 = x
b -8 = x
c = x
________
a+B+C=3x-12+4
a+b+c=3x-4

triplo menos 4, resposta A
Vamos chamar de X o número de cestas.
Setor A) se sobraram 12 cesta é porque o número de cestas (X) menos o número de empregados (A) é igual a 12: X-A=12
Setor B) se faltaram 8 cestas é porque o número de cestas (X) menos o número de empregados (B) é igual a -8: X-B=-8
Setor C) se não faltou nem sobrou é porque o número de cestas é igual ao número de empregados: X=C
Agora é só somar as três equações: A+B+C= X-12 + X+8 +X = 3X - 4 = a soma do número de empregados (A+B+C) é igual à soma do número de cestas (3X) menos 4 (-4).
1. Vamos chamar o número total de cestas de "N".
1. Comecemos pelo setor C...
N/C = 1 (uma cesta para cada, pois não sobra nem falta). Então, N = C
2. No setor B...Dividindo N por B, faltam 8 cestas. Ou seja, tem mais 8 cabeças no setor que vão ficar "chupando dedo", chorando...
B = N + 8 (se não tivessem esses 8 caras a mais, daria certinho uma cesta para cada)

3. No setor A...Dividindo N por A, sobram 12 cestas. Portanto, faltam 12 carinhas no setor A para o número de cestas dar certinho, ou seja, para o resultado dar um. Isso nos leva à seguinte equação: A = N-12
4. Agora é só somar...
N + (N+8) + (N-12)
3N - 4 = triplo do número de cestas básicas compradas, menos 4. - ALTERNATIVA A
Nesses tipos de questão, é só colocar um número qualquer na variável.

Nessa situação, coloquei o valor hipotético para o número de cestas como 20.

Dessa forma, seguindo as dicas pelo enunciado da questão, temos:

Setor A= 8 funcionários
Setor B= 28 funcionários
Setor C= 20 funcionários.

Somando-se os 03 valores, temos o total de 56 funcionários.

Ou seja, o triplo do total de cestas menos 04 é igual ao número de funcionários. Resposta: Letra A
S - Setor

C - Cestas

SA=C-12

SB=C+8

SC=C

Total da empresa = SA+SB+SC

Total da empresa = C-12 + C+8 + C

Total da empresa = 3C-4 - Resposta A

ID

1065523

Banca

INEP

Órgão

ENEM

Ano

2013

Provas

INEP - 2013 - ENEM - Exame Nacional do Ensino Médio - Primeiro e Segundo Dia

Disciplina

Matemática

Assuntos

Uma fábrica de fórmicas produz placas quadradas de lados de medida igual a y centímetros. Essas placas são vendidas em caixas com N unidades e, na caixa, é especificada a área máxima S que pode ser coberta pelas N placas.
Devido a urna demanda do mercado por placas maiores, a fábrica triplicou a medida dos lados de suas placas e conseguiu reuni-las em uma nova caixa, de tal forma que a área coberta S não fosse alterada.

A quantidade X, de placas do novo modelo, em cada nova caixa será igual a:

Alternativas

N/9

N/6

N/3

Comentários

Se a área do quadrado é igual a y^2 e na caixa cabem "N" peças a área da caixa será S = N x y^2. Depois da modificação, teremos pelo mesmo raciocínio um novo número de peças "N1": S1 = N1 x (3y)^2 ou S1 = N1 x 9y^2. Como é preciso manter a mesma área por força do enunciado: S = S1 então: N x y^2 = N1 x 9y^2. Isolando N1 : N1= N x y^2 / 9y^2 e resolvendo: N1 = N/9. É claro que N1 pode ser chamado de "x".
Regra de Três ( inversamente proporcional)
Tamanho(área) Unidades
Y^2 ------------------N
(3Y)^2---------------- X

Y^2 x N = 9Y^2 x X
X= N/9
Inicialmente

N . y² = S

Depois

x . (3y)² = S

Igualando as equações para relacionar x com N

N . y² = x . (3y)²

N . y² = x . 9y²

x = N / 9
A = Y x Y = Y^2
1 placa-------y^2
N placas-----S
S = N x Y^2
N x Y^2 = X x 9Y^2
9X = N
X = N/9
Letra A
Area do quadrado
Y x Y = Y2
aumentou 3x
3y x 3y= 9y2
regra de Três:
Y2______N
9Y2_____x
logo :: *são diretamente proporcionais
Y2N= 9Y2x
-corta os dois Y2
ficarara
N=9x
x= N/9
Espero ter ajudado <3

ID

1077205

Banca

VUNESP

Órgão

UNESP

Ano

2013

Provas

VUNESP - 2013 - UNESP - Assistente de Informática

Disciplina

Matemática

Assuntos

Em uma prateleira de certa farmácia, uma pilha contém 22 embalagens de um mesmo medicamento, algumas com 1,5 cm de espessura, com 10 comprimidos em cada, e outras com 4 cm de espessura, contendo 30 comprimidos cada uma. Sabendo que a altura dessa pilha é 63 cm, é correto afirmar que o número total de comprimidos contidos em todas as caixas dessa pilha é igual a;

Alternativas

460.

420

400.

380.

350.

Comentários

A+b = 22
15a + 40b = 630

A= 10
B= 12

10x10= 100
12x30= 360

100+360= 460
Embalagens de 1,5cm, com 10 comprimidos cada (A)
Embalagens de 4 cm, com 30 comprimidos cada (B)

Do enunciado temos que:
(I) são 22 caixas no total, logo: A + B = 22
(II) a altura da pilha é 63 cm, logo: (1,5 * A) + (4 * B) = 63, ou pra simplificar multiplique por 10 ==> 15A + 40B = 630
Com o sistema (I) e (II), chega-se a A=10 e B=12

Embalagens de 1,5cm, com 10 comprimidos cada (A) x 10 = 100 comprimidos
Embalagens de 4 cm, com 30 comprimidos cada (B) x 12 = 360 comprimidos
Total = 460 comprimidos

ID

1077361

Banca

VUNESP

Órgão

UNESP

Ano

2013

Provas

Disciplina

Matemática

Assuntos

Dois componentes líquidos, A e B, são utilizados na fabricação de certo produto. Sabe-se que 2,4 litros de A tem o mesmo preço que 2,8 litros de B. Desse modo, se 350 mL de B custam R$ 15,00, então o preço de 400 mL de A é igual a;

Alternativas

R$ 28,00.

R$ 25,00.

R$ 22,00.

R$ 20,00.

R$ 18,00

Comentários

1 - Achar o litro do Item B : Se 350 ml custa 15,00, 2800 ml custa 120 reais;
2 - Se 2,4 de item A custa igual a 2800 de B. Logo 400 Ml custará 20 reais.
2,4a=2,8b
__
0,35b=15
b=15/0,35
b=42,85
__
2,4a=2,8.42,86
2,4a=120
a=120/2,4
a=50
__
1000 ml A - 50
400 ml A - x
1000x=20000
x=20
Alternativa D
2800B-----------X
350B------------15
15×2800= 42000
42000/350= 120
2,8 B é igual a 120, no enunciado fala que
2,8 B tem o mesmo valor que 2,4 A:
2400A-------------120
400A---------------X
400×120= 48000
48000/2400= 20
400 ml A= 20

ID

1077526

Banca

VUNESP

Órgão

Faculdade Cultura Inglesa

Ano

2013

Provas

VUNESP - 2013 - Faculdade Cultura Inglesa - Vestibular - Prova 01

Disciplina

Matemática

Assuntos

O dono da lanchonete da escola colocou à venda todos os sanduíches que chegaram da cozinha industrial. No total, eram 108 sanduíches de atum, frango e queijo. A quantidade de sanduíches de atum era igual ao triplo da quantidade de sanduíches de frango, e a quantidade destes, por sua vez, era igual ao dobro da quantidade de sanduíches de queijo. Ao final do dia, não restaram sanduíches.

É correto afirmar que o número total de sanduíches de frango vendidos nesse dia foi igual a;

Alternativas

Comentários

atum+frango+queijo=108
a=3f
f=2q
subistituindo na 1ª expressão
3f+2q+q=108
3(2q)+2q+q=108
9q=108
q=12 se f=2q então frango=24
1)No total, eram 108 sanduíches de atum, frango e queijo. A quantidade de sanduíches de atum era igual ao triplo da quantidade de sanduíches de frango, e o de frango era igual ao dobro da quantidade de sanduíches de queijo. Ao final do dia, não restaram sanduíches.

Analisando o problema vemos que o sanduíche de atum diz: triplo (do frango)... e o de frango diz: dobro ( do queijo) e o de queijo não se diz nada, então começaremos por ele que receberá a variável X:
queijo: X
frango (dobro do queijo): 2X
atum (triplo de frango): 3(2X) = 6X
atum + frango + queijo = 108; Daí montamos a equação:
6x + 2x + x = 108
9x = 108
x = 12
queijo = X que vale 12
frango = 2X que vale: 2. 12 = 24 (que é a resposta da pergunta)
atum = 6X que vale: 6. 12 = 72
Vamos chamar de x = sanduíches de atum, de y = sanduíches de frango e de z sanduíches de queijo, assim, montando as equações abaixo:

108 = total de sanduíches, assim: x + y + z = 108, x = 3y e y = 2z. Substituindo em função de y:

3y +y + y/2 = 108 à 4.5 y = 108 à y = 24 sanduíches de frango.

Letra C.
Atum = x; Frango= y e Queijo= Z, o problema diz que: x+y+z= 108.
Diz tbm que: x (atum)= 3.(y), lembrando que y é frango
y (frango)= 2.(z), lembrando que z é queijo
Do z não diz nada.
x+y+z=108, Vamos substituir os termos? Se x é igual a 3Y, coloco 3y no lugar do X na equação, fica assim:
3y+y+z=108-------> 4y+z=108 ( Se o problema diz que y é igual a 2 z, 4y, será igual a 8z, certo ( y=2 z; 4y= 8z), ficará assim:
8z+z=108---------> 9z=108-------> z=108/9=12. Sabemos que z=12, e z é queijo.
Agora façamos as substituiçoes:
Frango= 2.z, então 2.12= 24
Concordo que não é o jeito mais fácil, porém foi o jeito que consegui fazer.
acho q escolhi o caminho mais complicado, porém resolvi de forma bem rápida...
sanduíches = 108
atum: A
frango: F
queijo: Q
A = 3F
F = 2Q -> Q = F/2
A+F+Q = 108 -> 3F + F + F/2 = 108 -> mmc:2 -> 6F + 2F + F = 216 -> 9F = 216 -> F=24
A quantidade total de sanduíches é igual a 108. O enunciado conta que a quantidade de atum é 3x maior que a de frago e a quantidade de queijo é a metade da de frango. Substituindo 24 no frango, multiplica por 3 no atum = 72 + 24 (de frango) = 96 + a metade da quantidade de frango (12) = 108!
x»atum| sendo x= 3y
y»frango| sendo y= 2z
z»queijo
! precisamos igualar os coeficientes, então, usando a proporcionalidade...
x=3(2z)=6z
[...]
6z+2z+z= 108
9z=108
z=12 pastéis de queijo
x= 6.12» 72 de atum
y= 2.12» 24 de frango
z=12 de queijo
LETRA C
APMBB

ID

1082689

Banca

CESPE / CEBRASPE

Órgão

MDIC

Ano

2014

Provas

CESPE - 2014 - MDIC - Agente Administrativo

Disciplina

Matemática

Assuntos

Com relação aos sistemas de equações lineares e às funções de 1.º e de 2.° graus, julgue os itens que se seguem.

Se Aldo, Pedro e Júlia confeccionarem, conjuntamente, 50 camisetas em uma semana; se a soma das quantidades confeccionadas por Aldo e Júlia for 2 unidades a mais que o dobro da quantidade confeccionada por Pedro; e se a quantidade confeccionada por Pedro for 3 unidades a menos que a quantidade confeccionada por Júlia, então Pedro confeccionará, nessa semana, mais de 15 camisetas.

Alternativas

Certo

Errado

Comentários

O comando da questão dá os seguintes dados:
A+P+J= 50
A+J= (2 . P) + 2
P= J - 3
Substituindo o P na segunda expressão, fica:
A + J = 2 . (J - 3 ) + 2
A + J = 2J - 4
A= J - 4
Substituindo a primeira expressão, fica:
(J - 4) + (J - 3) + J = 50
3J = 57
J = 57/3
J=19
Assim descobrimos que:
P= 19 - 3
P=16
E descobrimos que:
A + 16 + 19 = 50
A = 50 - 35
A = 15
Assim temos:
J= 19
P= 16
A = 15
Sendo assim a afirmação é CORRETA!
Muito bom o seu desenvolvimento Letícia, no entanto não precisava fazer tantas contas. Como a questão queria saber apenas a quantidade de Pedro, bastaria substituir na primeira linha do seu desenvolvimento: A + J = 2P + 2, corrija-me se estiver errado.
De acordo com enunciado, podemos montar as equações, logo:

A + P + J = 50 (1)

A + J = 2 + 2P (2)

P = J – 3 (3)

Resolvendo: (3) à (2)

A + J = 2 + 2(J – 3) à A = J – 4 (4)

Assim, (4) à (1)

(J - 4) + (J - 3) + J = 50

3J = 57

J = 57/3

J = 19

Assim, substituindo acharemos P = 16, A = 15 e J = 19
Resposta: Certo.
CORRETO.
A + P + J = 50 ------ A + J = 50 - P
A + J = 2P + 2
P = J - 3
Igualando os A + J:
2P + 2 = 50 - P
P = 16
Não tem nada de errado na resolução do colega Bárbaro MissãoPRF. Ele só não desenvolveu a resolução, porém a lógica, ou seja, a forma de resolver está correta. Mas vamos lá, no inteiro teor então:

ax+px+jx=50

ax+jx=2px+2

px=jx-3

2px+2=50-px

2(jx-3)+2=50-jx+3

2jx-6+2=50-jx+3

3jx=57

jx=19

Se jx=19, então, px=19-3=16 e ax+16+19=50 ====> ax=50-35=15.

Pedro confeccionou 16 > 15. CORRETO.
a + p + j =50

a + j = 2+2p

p = j - 3

Pedro confeccionará mais de 15 camisetas então vamos colocar 16 >>> p= 16

16 = j - 3

j=19

a+19 =2+2(16)

a= 15

15 + 16 + 19 = 50 ,logo correto mais de 15
Se Aldo, Pedro e Júlia confeccionarem, conjuntamente, 50 camisetas:

ALDO + PEDRO + JÚLIA = 50

ALDO = 50 - PEDRO - JÚLIA (1)

Se a soma das quantidades confeccionadas por Aldo e Júlia for 2 unidades a mais que o dobro da quantidade confeccionada por Pedro;

ALDO + JÚLIA = 2PEDRO + 2 (2)

Se a quantidade confeccionada por Pedro for 3 unidades a menos que a quantidade confeccionada por Júlia:

JÚLIA = PEDRO - 3 (3)

Dessa questão conseguimos retirar essas 3 equações acima, substituindo as equações 1 e 3 na equação 2 temos:

ALDO + JÚLIA = 2PEDRO + 2 (2)

50 - PEDRO - JÚLIA + PEDRO - 3 = 2PEDRO + 2

50 - PEDRO - (PEDRO - 3) + PEDRO - 3 = 2PEDRO + 2

50 - PEDRO - PEDRO + 3 + PEDRO - 3 = 2PEDRO + 2

50 - PEDRO = 2PEDRO + 2

50 - 2 = 3PEDRO

3PEDRO = 48

PEDRO = 48/3

PEDRO = 16

Nessa semana pedro confeccionou mais de 15 camisetas.

Gabarito Certo!
Se Aldo, Pedro e Júlia confeccionarem, conjuntamente, 50 camisetas

A + P + J = 50

Se a soma das quantidades confeccionadas por Aldo e Júlia for 2 unidades a mais que o dobro da quantidade confeccionada por Pedro

A + J = 2P + 2

Substituindo a 2ª equação na 1ª

A + P + J = 50

A + J + P = 50

2P + 2 + P = 50

3P = 48

P = 16

Pedro confeccionará 16 camisetas.

ITEM CORRETO

https://matematicasemsegredos.wordpress.com/
Pensei assim:

Se Aldo e Julia produziram o dobro mais +2 que pedro, levando em consideração o enunciado;

Pedro fez 15

o dobro +2 = 32

32+15=47

logo, Pedro teria que fazer mais de 15 camisetas para atingir as 50.

Como a questão pede se é mais de 15, nem precisa saber quanto é de fato, apesar de que, se você quer ter certeza é só aumentar:

Pedro =16

dobro + 2 =34

34+16=50

Força!!
Se pedro fez 15 camisas, julia fez 12 (15-3) e aldo fez 23 (15x2+2) = Total de 46 camisas, porém deve ser exatas 50 camisas, portanto Pedro pode ter confeccionado menos ou mais do que 15 camisas...

Para verificar se Pedro fez mais de 15 camisas:

Se pedro fez hipoteticamente 16 camisas, obrigatoriamente a julia terá que ter feito 13 (16-13) e aldo 21 (16x2+2). Temos portanto o total exato de 50 camisas. Com isso, Pedro fez exatas 16 camisas!
A + P + J= 50
A + J = 2 + 2P
P = j-3
2P + 2 + P = 50
3P = 48
P= 16
A+P+J = 50

A + J = 2.P + 2

Agora só fazer a substituição:

2.P + 2 + P = 50

3P = 48

= 16

CERTO!

ID

1089766

Banca

VUNESP

Órgão

CODESP-SP

Ano

2011

Provas

VUNESP - 2011 - CODESP-SP - Guarda Portuário

Disciplina

Matemática

Assuntos

A diferença e o produto entre o número de automóveis nacionais e importados em um estacionamento valem, respectivamente, 15 e 16. O total de automóveis nesse estacionamento é

Alternativas

17.

19.

23.

29.

31.

Comentários

Letra A
n = nacionais e i = importados
n - i = 15 -> n = 15 + i
n*i = 16 -> (15 + i)*i = 16 -> 15i + i² = 16
i² + 15i - 16 = 0
▲ = 225 - 4*1*(-16) = 289
i = (-15 ± 17)/2
i1 = 1
i2 = - 16 (o número de carros não pode ser negativo)
Carros importados = 1
n = 15 + i = 15 + 1 = 16
Carros no estacionamento = n + i = 16 + 1 = 17
Oque aconteceu como 225? de onde vem o -15?

Pois a raiz esta subtraindo o 225 tambem, e não pode, já que ele é o B^2 = 15^2

O correto não seria: i 225 - [√4*1*(-16) = 289]
X-Y=15
X.Y=16 >>> X=16/Y SUBSTITUI NA PRIMEIRA EQUACÃO:
16/Y-Y=15
16-1/Y=15
15Y=15
Y=1 , SUBSTITIUNDO NA PRIMEIRA EQUACAO TEMOS:
X-1=15 >>>> X=16
SE X=16 E Y=1 O TOTAL DE CARROS É:

(A) 17.

ID

1089778

Banca

VUNESP

Órgão

CODESP-SP

Ano

2011

Provas

VUNESP - 2011 - CODESP-SP - Guarda Portuário

Disciplina

Matemática

Assuntos

Em uma cidade, a razão do número de carros para o número de motos é de 3/7. Todos os carros dessa cidade têm 4 pneus, e todas as motos têm 2 pneus. Em determinado dia, os donos de todos esses carros e motos decidiram calibrar todos os pneus de seus veículos. Sabendo que o total de pneus calibrados foi 234, conclui-se que a diferença entre o número de motos e o de carros, nessa cidade, é de

Alternativas

20.

24.

28.

32.

36.

Comentários

Gabarito: E

Proporção de Veículos

A cada 10 veículos, 3 são carros e 7 são motos.

A cada 10 veículos, há 26 pneus (o enunciado diz que carros são 4 pneus e motos 2 pneus, então 4x3 carros= 12; 2x 7= 14, soma tudo> 12 + 14= 26)

REGRA DE TRÊS

Veículos Pneus
10 26
x 234 (qtde de pneus calibrados)

26x= 2340
x= 90 veículos (então neste dia foram calibrados 90 veículos entre motos e carros).

Se a proporção de carros e motos é de 3/7, então

Veículos Motos
10 7
90 y

10y= 630
y= 630/10
y= 63 motos

Valor total de Veículos: 90 - 63 motos= 27 carros

O exercício pede a diferença entre o número de motos e o número de carros

63(motos) - 27 (carros)= 36
4C+2M=234 (3)

7C-3M=0 (2)

12C+6M=702

14C-6M=0

26C=702

C=27

M=63

63-27=36

Gabarito E
GABARITO = E

Para cada 3 Carros, há 7 motos. O problema trabalha com pneus, logo, vamos converter para pneus.

1 carro = 4 pneus ------> 3 carros = 12 pneus

1 moto = 2 penus ------> 2 motos = 14 pneus

Se foram calibrados 234 pneus proporcionalmente ao número de pneus calibrados de carros e motos ( 12 para 14) então vamos encontrar suas constante:

12k + 14K = 234

K = 9 Constante de proporcionalidade.

Agora multiplicamos a constante pelas proporções de pneus.

Carros = 12k >>>> 12 X 9 = 108 pneus calibrados de carros

Motos = 14k >>>> 14 X 9 = 126 pneus calibrados de motos.

Pronto. Agora so fazer a regra de 3.

Se 1 carro tem 4 pneus, então 108 pneus terá em 27 carros.

Se 1 moto tem 2 pneus, então 126 pneus terá em 63 motos.

A questão quer a diferença entre carros e motos.

63 motos - 23 carros = 36
CARROS/MOTOS = 3/7
3/7.4/2 = 12/14
(número de pneus)
12+14=26
(total de pneus em uma vez da razão)
234/26=9
(total de vezes que a quantidd de pneus da razão coube dentro do total)
3.9=27; 7.9=63
(total de carro e moto)
63-27= 36 (diferença entre as quantdd)

ID

1089793

Banca

VUNESP

Órgão

CODESP-SP

Ano

2011

Provas

VUNESP - 2011 - CODESP-SP - Guarda Portuário

Disciplina

Matemática

Assuntos

Ariel e Bernardo, juntos, fazem uma maquete em 4 horas. Bernardo e Célio fazem a mesma maquete em 6 horas. Ariel e Célio precisam de 8 horas para fazer essa maquete. Considerando a velocidade individual desses três garotos na confecção da maquete, pode-se concluir que

Alternativas

Ariel é mais rápido que Bernardo.

Célio é mais rápido que Ariel.

Bernardo é mais rápido que Célio.

Ariel é o mais lento dos três.

Bernardo é o mais lento dos três.

Comentários

Alguém sabe responder, por favor.

Nas minhas contas A+B+C deu 9
E então Ariel 3, Bernardo 1 e Célio 5 :(
Ariel e Bernardo = 4h
Bernardo e Célio = 6h
Ariel e Célio = 8h

Ariel = 2h+4h = 6h
Bernardo = 2h+3h = 5h
Célio = 3h+4h = 7h

Bernardo é o mais rápido e Célio é o mais lendo.
Portanto, Bernardo é mais rápido que Célio.
Alternativa: C
Mais detalhadamente:
1º Passo: Ariel e Bernardo, juntos, fazem uma maquete em 4 horas. Levando-se em conta que cada um faz metade da maquete, cada um leva 2 horas para fazer a parte que lhes cabe.
2º Passo: Bernardo e Célio fazem a mesma maquete em 6 horas. Seguindo o mesmo raciocínio, levando-se em conta que cada um faz metade da maquete, cada um leva 3 horas para fazer a parte que lhes cabe.
3º Passo: Ariel e Célio precisam de 8 horas para fazer essa maquete. Ainda seguindo o mesmo raciocínio, levando-se em conta que cada um faz metade da maquete, cada um leva 4 horas para fazer a parte que lhes cabe.

Assim, considerando a velocidade individual desses três garotos na confecção da maquete, pode-se concluir que:
Ariel: 2h +4h = 6h (soma das horas de Ariel do primeiro passo e do terceiro passo)
Bernardo: 2h+3h = 5h (soma das horas de Bernardo do primeiro passo e do segundo passo)
Célio: 3h+4h = 7h (soma das horas de Célio do segundo passo e do terceiro passo)

A partir desse raciocínio, concluímos que Bernardo é o mais rápido e Célio é o mais lendo.
A alternativa que tem algo que envolva essa conclusão é que Bernardo é mais rápido que Célio.
Alternativa: C
Lívia Pozzobon
Muito obrigada! Ajudou muito!
Deus a abençõe.
A+B=4

B+C=6

A+C=8

Resolve os sistemas e descobre que A=3h, B=1h e C=5h

O mais lento de todos é Célio, que demora 5h. Bernardo é mais rápido que Célio, pois B demora 1h e C demora 5h.

Gabarito C
(i) A + B = 4 >>>>>> A = 4 - B

(ii) B + C = 6 >>>>>>C = 6 - B

(iii) A + C = 8

---------------------------

(iii) 4 - B + 6 - B = 8

-2B = -2

B = 1h substituindo >>>> A = 3h e C = 5h

B é o mais rápido, letra C gabarito

ID

1089805

Banca

VUNESP

Órgão

CODESP-SP

Ano

2011

Provas

VUNESP - 2011 - CODESP-SP - Guarda Portuário

Disciplina

Matemática

Assuntos

Elias queria guardar sua coleção de revistas e, para isso, dispunha de um certo número de caixas de igual tamanho. Como todas as revistas também tinham o mesmo tamanho, Elias tentou, primeiro, guardar 10 revistas por caixa, mas, fazendo assim, uma caixa ficou vazia. Em seguida, tentou guardar 9 revistas por caixa, mas, desse modo, 39 revistas ficaram fora das caixas. Finalmente, Elias decidiu comprar mais caixas iguais à que ele tinha, de maneira que em cada caixa ele guardasse exatamente 8 revistas. O número de caixas que Elias deve comprar é

Alternativas

10.

11.

Comentários

Pessoal, alguém conseguiu resolver essa???
Eu consegui fazer por sistemas
C= quantidade de caixas
R= quantidade de revistas

1ª expressão
R/10 = C-1 ou melhor R = (C-1) * 10
2ª expressão
R= (9.c)+39

Substituindo fica: 9c+ 39= (c-1)*10
A resposta será 49 caixas e 480 revistas.
Depois 480 revistas/8 em cada caixa = 60 caixas.
Se Elias já tinha 49 caixas e precisa de 60, então faltam 11.

Espero ter ajudado.
Seja "r" o número de revistas e "c" o número de caixas.

Como a divisão de 10 revistas por caixa fez sobrar 1 caixa, se Elias tivesse uma caixa a menos, o número de revistas seria igual a 10 vezes o número de caixas. Portanto, podemos escrever que:

r = 10.(c - 1)

r = 10c - 10 (equação I)

De forma análoga, se retirássemos 39 revistas da pilha, poderíamos guardar 9 revistas por caixa. Portanto, podemos entender que:

r - 39 = 9.c

r = 9.c + 39 (equação II)

Igualando as equações acima, teremos:

10c - 10 = 9c + 39

10c - 9c = 39 + 10

c = 49

Substituindo o valor de "c" em qualquer das equações, poe exemplo na equação I:

r = 10.c - 10

r = 10.49 - 10

r = 490 - 10

r = 480

Portanto, Elias possuía 480 revistas e 49 caixas.

Para que ele guarde exatamente 8 revistas por caixa, teremos que:

r = 8.c

480 = 8.c

c = 480 / 8

c = 60 caixas.

Como Elias já possui 49 caixas, ele precisa comprar:

60 - 49 = 11 caixas.

Resposta: Alternativa (E)

Fonte: Yahoo Respostas

ID

1092460

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

ID

1092463

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

Considerando que um sistema linear possua função de transferência.
H(s) = s(s - a )
( s - b )(s - c)

em que a, b e c são constantes reais, e em que a ≠, b ≠ e c ≠ e s é a variável de Laplace, julgue os itens a seguir.

Esse sistema possui ganho nulo em regime permanente.

ID

1092466

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

Alternativas

Certo

Errado

Comentários

Sistema de fase não-mínima. Apresenta um zero no semi-plano direito!

ID

1092469

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

Considerando que um sistema linear possua função de transferência.
H(s) = s(s - a )
( s - b )(s - c)
em que a, b e c são constantes reais, e em que a ≠, b ≠ e c ≠ e s é a variável de Laplace, julgue os itens a seguir.

Ao se esboçar o lugar geométrico das raízes para esse sistema, um dos polos em malha fechada deverá tender a –∞ com o aumento do ganho de realimentação.

ID

1092472

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

Considerando que um sistema linear possua função de transferência.
H(s) = s(s - a )
( s - b )(s - c)

em que a, b e c são constantes reais, e em que a ≠, b ≠ e c ≠ e s é a variável de Laplace, julgue os itens a seguir.

Se b = - 2 e c = - 1, então esse sistema será estável.

ID

1092475

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

x = Ax + Bu
y = Cx + Du

Considere a representação usual de sistemas lineares no espaço de estados apresentada acima, em que x ∈ Rⁿ , u ∈ R^p e y ∈ R^msão os vetores de estados, de entradas e de saídas, respectivamente, e A, B, C e D são matrizes de dimensões apropriadas. A respeito desse sistema, julgue os itens seguintes.

Os polos do sistema são sempre os elementos da diagonal da matriz A.

ID

1092478

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

x = Ax + Bu

y = Cx + Du

Considere a representação usual de sistemas lineares no espaço de estados apresentada acima, em que x ∈ Rⁿ , u ∈ R^p e y ∈ R^msão os vetores de estados, de entradas e de saídas, respectivamente, e A, B, C e D são matrizes de dimensões apropriadas. A respeito desse sistema, julgue os itens seguintes.

Para determinado sistema, existe um único valor para cada uma das matrizes A, B, C e D na representação em espaço de estados.

ID

1092481

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

ID

1092484

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

x = Ax + Bu
y = Cx + Du

Considere a representação usual de sistemas lineares no espaço de estados apresentada acima, em que x ∈ Rⁿ , u ∈ R^p e y ∈ R^msão os vetores de estados, de entradas e de saídas, respectivamente, e A, B, C e D são matrizes de dimensões apropriadas. A respeito desse sistema, julgue os itens seguintes.

Esse sistema será controlável se a matriz de controlabilidade do sistema tiver posto completo.

Alternativas

Certo

Errado

Comentários

ficaram sem contratação

ID

1092487

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

x = Ax + Bu
y = Cx + Du

Considere a representação usual de sistemas lineares no espaço de estados apresentada acima, em que x ∈ Rⁿ , u ∈ R^p e y ∈ R^msão os vetores de estados, de entradas e de saídas, respectivamente, e A, B, C e D são matrizes de dimensões apropriadas. A respeito desse sistema, julgue os itens seguintes.

Para determinar se o sistema é observável, deve-se fazer uma análise envolvendo as matrizes A e B.

ID

1092490

Banca

CESPE / CEBRASPE

Órgão

INPE

Ano

2008

Provas

CESPE - 2008 - INPE - Tecnologista Júnior - TS12

Disciplina

Matemática

Assuntos

x = Ax + Bu
y = Cx + Du

Considere a representação usual de sistemas lineares no espaço de estados apresentada acima, em que x ∈ Rⁿ , u ∈ R^p e y ∈ R^msão os vetores de estados, de entradas e de saídas, respectivamente, e A, B, C e D são matrizes de dimensões apropriadas. A respeito desse sistema, julgue os itens seguintes.

A função de transferência do sistema é dada por C ( sI - A)^-1 B + D, em que I é a matriz identidade

ID

1103992

Banca

UNEMAT

Órgão

PM-MT

Ano

2012

Provas

UNEMAT - 2012 - PM-MT - Aspirante da Polícia Militar - 1° dia

Disciplina

Matemática

Assuntos

Pedro fez um concurso cujas provas tinham um total de 100 questões. Para cada questão resolvida corretamente, seriam atribuídos três pontos e seriam retirados dois pontos por questão não resolvida ou resolvida incorretamente. Pedro obteve 20 pontos no concurso.

O número de questões resolvidas corretamente por Pedro é:

Alternativas

Comentários

Mais fácil jogar com as alternativas:

4x44 = 132

2x56 = 112

132-112 = 20 pontos.
GAB A

Pedro fez um concurso cujas provas tinham um total de 100 questões. Para cada questão resolvida corretamente (C CERTO ) , seriam atribuídos três pontos e seriam retirados dois pontos por questão não resolvida ou resolvida incorretamente( R ERRO). Pedro obteve 20 pontos no concurso.

C + R = 100 (SUBSTITUI UMA LETRA NA OUTARA)
C3 + R-2 = 20

R-2 3 . ( R + 100) = (20 FAZER A DISTRIBUTIVA)
R-2 + 3R 300 = 20 (O -2R ESTAVA DIMINUINDO PASSA SOMANDO JUNTO COM O 3R )
5R 300 - 20 = 280 (DIVIDE 280 POR 5R)

280/ 5R = 56 = R SE ELE ERRO 56 PARA ACHAR AS QUE ELE ACERTO E SÓ FAZER 56 - 100 = 44 C

COM DEUS HOJE E SEMPRE!!!!

ID

1121818

Banca

CS-UFG

Órgão

UEAP

Ano

2014

Provas

Disciplina

Matemática

Assuntos

Em um determinado mês, uma garota gastou R$ 75,00 de sua mesada comprando milk-shakes no shopping. Além disso, comprou ingressos para o cinema e pipoca. O valor gasto por ela com pipoca correspondeu ao dobro do valor gasto com os ingressos para o cinema e representava um quarto do valor da sua mesada naquele mês. Tendo em vista essas condições, o valor da mesada nesse mês foi de:

Alternativas

R$ 103,12

R$ 120,00

R$ 195,00

R$ 200,00

Comentários

Respondi por eliminação. Tentei os valores mais exatos, no qual as contas tornam mais fáceis. Primeiro tentei com a alternativa d)200,00 não deu, aí fui direto para a b)120,00 e deu certo.
1/4 de 120= 30,00 = Pipoca + 15,00 (Ingressos é a metade do valor gasto com pipoca) + 75,00 (milk-shakes) = total 120,00 = Valor da mesada.
T = P + I + M (Total, Pipoca, Milk-shake)
Pelo enunciado: P = 2.I e 2I=1/4.T
Substituindo na equação do total:
T = 2I + I + MT = 3I + M

Sabendo que I = T.1/8. e M = 75:
T = 3.T/8 + 75
(...)
T = 120
Fiz assim,

Organizei as informações:

Milk-shake (M) = R$ 75,00

Ingresso (i)= i

Pipoca (P)= 2i => que é igual a 1/4

Mesada = M+i+P

ou

Mesada = 2i + 3/4 - Explicando: sendo 2i - 1/4 o que falta da mesada é = 3/4.

Sabendo que 2i = 1/4 - então, X = 3/4 - apliquei uma regra de três para saber quantos (i) valem o X a fim de encontrar o valor de i, vamos lá:

2i = 1/4

X = 3/4

Resolvendo a regra de três:

2i x 3/4 = X x 1/4 => 6i/4 = X/4 => Isolando o Xi, o denominador (4) passa para o outro lado multiplicando, ficando:

24i/4 = X

6i = X -> logo, 6i = 3/4 do total da mesada

Obs: na regra de três como os denominadores são iguais, podemos corta-los.

OK! Voltando a fórmula da mesada

Mesada = 1/4 + 3/4 ou mesada = 21 + 6i => mesada = 8i

Mesada (8i) = M (R$ 75,00) + i (i) + P (2i) => isolando o i:

8i - i - 2i = 75

5i = 75

i = 15

Achando o valor de I é só substituir:

Mesada = 8i => Mesada = 8 x 15 => Mesada = 120
Uma informação que não foi dada, que poderia ser passível de tornar a questão anulada, seria dizer que após todos esses gastos, ela gastou a mesada por completo.
De acordo com os dados do enunciado temos:
X = o total da mesada, M = milk-shakes, P = pipoca e I = ingresso.

X=P+I+M

Sendo que P = 2I = ¼ X, substituindo:

X = 2I + I + M = 31 + M = 3. ^X⁄₈ + 75 → X = 120,00.
Letra B.
GAB B

ID

1128553

Banca

CS-UFG

Órgão

UEAP

Ano

2014

Provas

Disciplina

Matemática

Assuntos

Para compor um produto usando os pesos em gramas x, y, z de três componentes químicos, respectivamente, deve-se obedecer à seguinte receita: o peso x do primeiro componente é igual ao dobro do peso y do segundo componente, o peso dos três juntos deve ser 1000 g e o peso z do terceiro deve superar em 100 g a soma dos pesos dos dois primeiros componentes. A solução do sistema correspondente é:

Alternativas

x=200, y=100, z =700

x=150, y=300, z =600

x=300, y=150, z =550

x=250, y=125, z =450

Comentários

X= 2y, Y=?; Z= x+y+100
X+Y+Z=1000
Substitui os valores:
2y+Y+2y+Y+100=1000, agora soma os y:
6y+100=1000, agora passa o 100 que esta somando para o outro lado, invertendo o sinal para subtrair
6y=1000-100
6y=900, agora passa o 6 que esta multiplicando para o outro lado, invertendo o sinal para dividir
Y=900/6, Y=150
Agora é só substituir os valores na expressão
X+Y+Z=1000
X=2*150; Y=150 ;Z= 2*150+150+100
X=300 + Y= 150 + Z=300+150+100=550
Resolvendo o sistema linear de acordo com as informações do enunciado:

Logo temos x = 300, y = 150 e z = 550.

Resposta letra C.
X - A = (2xb)
y - B
Z - C = (2xb+b+100g)
A+B+C = 1000G
(2XB)+B+(2XB+B+100)=1000
2B+B+2B+B+100=1000
4B+2B+100=1000
6B=1000-100
6B=900
B=900/6
B=150 Logo: Y=150
Substituindo as demais:
X = (2xb) =2x150 = 300
Z = (2xb+b+100g) = 2x150+150+100 = 550
RESPOSTA LETRA C
Respondendo pelo raciocínio lógico: O enunciado fala que o total dos 3 componentes é igual a 1000g, somando os valores dados nas opções, as alternativas "B" e "D" chegar a valores diferentes (B=1050; D=825). Em outro ponto o enunciado diz "o peso z do terceiro deve superar em 100 g a soma dos pesos dos dois primeiros componentes.", ou seja, Z=(X+Y) + 100, na alternativa "A" x+y = 200+100 = 300 e z = 700, logo z nesse caso é 400 a mais do somatório de x+y, sobrando apenas a alternativa C.
Da pra resolver pegando o resultado e observando z

Z deve ser 100 a mais da soma de x+Y

A unica letra onde isso ocorre é a c x+y = 450 e z 550

450 + 550 = 1000
1°) X=2Y

2°) Z=X+Y+100

3°) X+Y+Z=1000

Vamos achar Y primeiro substituindo o 1°) e 2°) no 3°) fica:

X+Y+Z=1000

2Y+Y+X+Y+100=1000 (Substitui o X de novo, sendo que X=2Y) fica:

2Y+Y+2Y+Y+100=1000

6Y=900

Y=150 (Substitui no 1°) para achar X) fica:

X=2Y

X=2 (150)

X=300

Por fim vamos achar:

Z=X+Y+100

Z=300+150+100

Z=550

ID

1131472

Banca

EXATUS

Órgão

PM-ES

Ano

2013

Provas

EXATUS - 2013 - PM-ES - Soldado da Polícia Militar

Disciplina

Matemática

Assuntos

Quatro amigos, Abel, Bruno, Caio e Daniel, são colecionadores de figurinhas. Sabe-se que Abel possui metade da quantidade de figurinhas de Daniel mais um terço da quantidade de figurinhas de Caio; que Bruno possui o dobro da quantidade de figurinhas de Caio mais a quarta parte da quantidade de figurinhas de Daniel; que Daniel tem 60 figurinhas, e que Abel e Bruno possuem a mesma quantidade de figurinhas. Os quatro amigos possuem, juntos:

Alternativas

125 figurinhas.

128 figurinhas.

130 figurinhas.

132 figurinhas

135 figurinhas.

Comentários

Se D/2 + C/3 = 2C + D/4, então C = 9.
Substituindo os valores, ficarão: A = B = 33 fig; C = 9 fig e D = 60 fig, portanto terão 135 figurinhas.
A=1/2D + 1/3C A=30+1/3C

B=2C + 1/4D B=2C+15=

D=60

A=B

30+1/3C=2C+15 -2C+1/3C=-30+15 -2C+1/3C=-15 TIRA O MÍNIMO) -6C+C=-45 5C=45 C=9

B=2C+15 B=2*9+15 B=33 A=B A=33

33+33+9+60=135

ID

1142965

Banca

FGV

Órgão

FUNARTE

Ano

2014

Provas

Disciplina

Matemática

Assuntos

Carla faz doces caseiros de diversos sabores vendidos em potes de 1 litro e Dalva faz tortas, também de diversos tipos, mas todas com o mesmo tamanho. Carla vende cada pote de doce por R$24,00 e Dalva vende cada torta por R$36,00. Certa semana elas venderam 108 unidades dos seus produtos (total de potes e tortas) e Dalva arrecadou R$288,00 a mais que Carla.

O número de potes de doce que Carla vendeu foi:

Alternativas

36;

42;

48;

50;

60.

Comentários

Carla +Dalva = 108 unidades .......D=108 -C
36.Dalva = 288 + 24.Carla /12 ===3 D = 24 +2 C
SUBSTITUINDO
3 (108 - C ) = 24 + 2 C
324 - 3 C = 24 +2 C
300 - 5C =0
C= 60
Luciana, desculpe mas não consegui entender, pode explicar novamente?
Eu fiz meu calculo desta forma
Doces + tortas= 108
Dalva arrecadou R$ 288 a mais que Carla
O produto de Dalva custa R$ 36
Dividi 288 por 36= 8
D+T=108 (foram vendidas 8 tortas a mais que doces) T= D+8
D + D+8=108
2D=108-8
D=100/2
D=50
Pensei na resposta de Luciana e de fato meu raciocínio anterior estava equivocado
Dalva vende cada torta por R$ 36
Carla vede cada doce por R$ 24
As duas jutas venderam 108 mas Dalva ganhou R$288 a mais, não podemos esquecer que o produto de Dalva é mais caro
logo:
C+D= 108
D=108-C
Colocando os valores:
36D=24C+288 (simplificando todos estes valores por 12)
3D=24C+288 ( NOTEM QUE TEMOS DUAS LETRAS, MAS LÁ ENCIMA AFIRMAMOS QUE D=108-C)
SUBSTITUINDO:
3*(108-C)2C+24
324-3C=2C+24
5C=300
C=60
O raciono é o seguir. Segue as explicações que aprendemos na escola sobre sistema com incógnitas. 8º Ano.
1º passo - Não sabemos quantos potes de doce Carla vendeu e não sabemos quantas tortas Dalva vendeu, mas sabemos o total de unidade vendidas ( 108 unidades). Posso dizer que o total de doces é X e o total de tortas Y, então X + y = 108 e que X = 108 - y.
2º passo - Completando o sistema posso dizer que R$ 24,00 vezes X (X são o total de doces) + 288 (diferença a mais das tortas) = R$ 36,00 (valor das tortas)
3º passo - O sistema fica assim ------- X + y = 108 onde X = 108 - y
                                            24X + 288 = 36y agora é só substitui o X pelo seu valor. Veja como fica
24 . (108-y) + 288= 36y --------- multiplica 24 vezes 108 e 24 vezes y
2592 - 24y + 288 = 36y ------- lembrete importante( só pode ficar antes da igualdade os números com incógnitas e após os números    sem incógnitas. (obs. quando for preciso mudar os números para antes ou depois da igualdade tem que trocar os sinais. Veja. -24y - 36y = - 2592 - 288
   - 60y = - 2880 (-1) (O número com variável não pode ficar negativo, por isso multipliquei por - 1)
            60y = 2880
                y = 2880/ 60 = 48 são as tortas vendidas por Dalva. agora é só substitui X = 108 - y X = 108 - 48 = 60 são os potes de doces vendidos por Carla. Resposta - E.
De acordo com o enunciado e considerando P o total de potes vendidos por Carla e T o total de tortas vendidas por Dalva, tem-se:

P + T = 108 eq I

36T – 288 = 24P eq II

Assim, T = 108 – P. Substituindo na eq II, tem-se:

36 (108 – P) – 288 = 24P

3888 – 36P – 288 = 24P

3600 = 60P

P = 60 potes
Resposta E)
Professor,

Vocês podiam colocar passo a passo os cálculos né? porque não adianta nada escrever e ter gente que não entendi como você chegou nesse resultado....

36T – 288 = 24P

Por que eu subtraio o valor unitário da torta do valor que ela arrecadou e igualo ao ao valor unitario do pote????
Galera, eu sei que é importante saber fazer os cálculos montando as equações, mas para quem tem dificuldade, como eu, para montar as equações e fazer os cálculos, usem a seguinte estratégia em questões como essa:
Ele quer saber o nº de potes de doces que carla vendeu, as possibilidades estão nas alternativas. E ele tb já deu o valor das unidades. Vá pelas tentativas dos resultados das alternativas, já sabendo que possivelmente Carla vendeu mais unidades:
Carla: 60 X R$ 24,00= R$ 1440
Dalva: 48 X R$ 36= R$ 1728
1728-1440=288,00, que é a diferença entre as vendas das duas.
Então Carla vendeu 60 unidades
Eu ganho tempo assim nesse tipo de questão
Raphael, já reclamei tanto sobre isso, mas nem retorno me dão. Eu ficava irritado quando a galera ficava postando os gabaritos e não entendia porque eles faziam isso, até que vi alguém dizendo que é por conta do limite diário de questões.
Agora nem ligo mais, até entendo porque o povo não quer pagar.
Aqui tem ótimos professores, mas quando tem um que não é bom e a gente reclama, ficamos a ver navios...
Dados conhecidos:

C + D = 108 (unidades)
D = C + 288 (valores)
Não devemos misturar as unidades com valores então vamos montar a formulá:
C/24 + D/36 = 108 substituindo C/24 + C+288/36 = 108
Resolvendo:
3C/72 + 2C/72 + 576/72 = 108
C = 1440 / 24 = 60
Doces: 24 (I) 36T - 24D = 288

Tortas: 36 (ll) T+D = 108 = T = 108- D

Então: 36 (108 - D) - 24D= 288

3888 - 36D - 24D = 288

-60D = - 3600 (-1)

D = 60

Resposta: E
Outra maneira de resolver seria

Os R$288,00 de renda a mais que Dalva obteve representa uma venda de 8 tortas. Logo, sobram 100 unidades, certo?

Como o valor unitário do produto da Carla é menor (R$24,00), das 100 unidades que restaram ela tem que vender mais unidades que a Dalva (R$36,00) para equiparar o valor a ser recebido ( pelas duas) das vendas das 100 unidades. Lembrando que o valor extra (R$288,00) não se aplica nessas 100 unidades, sendo assim aqui deve-se dividir igualmente o valor a ser recebido.

Dividindo as 100 unidades em partes iguais, daria 50 unidades para cada. Como Carla tem que vender mais, basta olhar as alternativas e ver que a única possível é 60 unidades. (se não sentir firmeza, basta tirar a prova)
Nessa eu fui no raciocínio.
A questão fala que Dalva saiu com 288 reais a mais, logo dividindo esse valor pelo preço da torta sabe-se que corresponde a 8 tortas. logo como a questão fala que eram 108 unidades, já podemos tirar oito, pois 8 tortas foram vendidas de diferença. Logo sobraram 100 unidades, e temos que igualar o pagamento das duas pois a diferença já foi paga à Dalva. Sendo assim, como o doce é mais barato que a torta, obviamente não podemos dividir 50 para cada, pois, Carla sairia no prejuízo. Então o único número que sobra superior a 50 é 60.
Ou seja, para que Carla e Dalva ganhem a mesma quantia, fora a diferença de 288, é necessário que Carla venda 60 doces.
Letra E
seguindo o raciocínio da galera ai eu fiz o seguinte
c+d= 108 c= 108-d36d = 24 c + 288 divide tudo por 12

3 d = 2c + 24

3d = 2 . 108 - 2d + 24

3d + 2d = 216+ 24

5d = 240 ---) d = 48 ( este 48 deve tirar os 8 amais no enunciadoentao 40 D e 60 C
O ponto chave da questão é: quantos reais Carla precisa vender para igualar Dalva?

Dalva = Carla + 288,00

ID

1153051

Banca

FCC

Órgão

TRT - 15ª Região (SP)

Ano

2013

Provas

FCC - 2013 - TRT - 15ª Região - Analista Judiciário - Área Administrativa

Disciplina

Matemática

Assuntos

Alternativas

número de cestas básicas compradas, mais 4.

dobro do número de cestas básicas compradas, mais 20.

triplo do número de cestas básicas compradas, menos 4.

triplo do número de cestas básicas compradas, mais 4.

número de cestas básicas compradas, menos 4.

Comentários

suponhamos que compramos 100 cestas

A= 88 pessoas
B= 108 pessoas
C=100 pessoas
=296, ou seja, o triplo de cestas compradas, menos 4.
Resposta c.
Equacionando:
Número de Cestas Básicas = Funcionários = NCB
Setor A = NCB - 12
Setor B = NCB + 8
Setor C = NCB
Somando-se os setores (A + B + C) e substituindo, temos:
NCB - 12 + NCB + 8 + NCB = 3*NCB - 4 (O triplo de cestas básicas menos 4)
Muito mais simples do que parece:
X = A + 12
X = B - 8
X = C

3X = (A + 12) + (B - 8) + C
3X = A + B + C + 12 - 8
3X = A + B + C + 4
ou seja:
A + B + C = 3X - 4
Inicialmente temos:
                                     A - 12 + B + 8 + C
Considerando que X = número de funcionários por setor, temos:
                                     X - 12 + X + 8 + X
                                         =  3x - 4
Com isso, o total de funcionários dos três setores é o triplo do número de cestas menos 4.
Se fossem distribuídas para todos os funcionários do setor C, não faltariam nem sobrariam cestas básicas.
C
Se as cestas fossem distribuídas para todos os funcionários do setor A, sobrariam 12 cestas:
C - 12 (-12 PORQUE SOBRARAM 12 CESTAS)
Se elas fossem distribuídas para todos os funcionários do setor B, faltariam 8 cestas.
C + 8 (+8 PORQUE FALTARAM 8 CESTAS PARA COMPLETAR C)
-------------------------------------
C + C - 12 + C + 8 = 3C - 4

ID

1167721

Banca

VUNESP

Órgão

CETESB

Ano

2013

Provas

VUNESP - 2013 - CETESB - Técnico Administrativo - Recursos Humanos

Disciplina

Matemática

Assuntos

Alternativas

R$ 4,80.

R$ 4,50

R$ 3,20

R$ 3,00.

R$ 2,80.

Comentários

(A) 2G + 3M + 1P = 21,20
(B) 3G + 2M + 1P = 22,80
(C) 3G + 3M + 3P = 30,00
----------------------------------
(C simplificada) G + M + P = 10,00 (vai ser usada no final)

(...)

(C) 3G + 3M + 3P = 30,00
(A) 2G + 3M + 1P = 21,20 .(-1)
---------------------------------
G + 2P = 8,80
G = (8,80 - 2P)

(...)

(C) 3G + 3M + 3P = 30,00
(B) 3G + 2M + 1P = 22,80 .(-1)
---------------------------------
M + 2P = 7,20
M = (7,20 - 2P)

A diferença de preço entre a pasta mais cara e a pasta mais barata
(C simplificada) G + M + P = 10,00
G + (7,20 - 2P) + P = 10,00
G - P = 10,00 - 7,20
G - P = 2,80
RESPOSTA E

Créditos: http://brainly.com.br/tarefa/8480
✅ Alternativa E
- Primeiro vamos montar os sistemas com as informações do enunciado:
2G + 3M + P = 21,20
3G + 2M + P = 22,80
3G + 3M = 3P = 30,00
- Agora vamos resolver as duas primeiras equações do sistema pelo método da soma, mas multiplicando a primeira por "-1" para inverter os sinais:
3G + 2M + P = 22,80
-2G -3M -P = 121,20
G - M = 1,60

G = 1,60 + M
- Sabendo que o valor de G é 1,60 + M, como vimos a cima, vamos substituir o valo de G ma primeira equação. Ficará assim:
2G + 3M + P = 21,20 => 2.(1,60 + 2M) + 3M + P = 21,20

Resolvendo:

3,20 + 2M + 3M + P = 21,20

5M + P = 18,00

P = 18 - 5M
- Repare que se simplificarmos a última equação do sistema por "10" ficaremos com G + M + P = 10, e é nessa equação que substituiremos os dados que já temos:
G = 1,60 + M
P = 18 - 5M

Resolvendo:

G + M + P = 10

1,60 + M + M + 18 - 5M = 10

-3M = 10 - 19,60

M = 3,20
- Pronto! Agora que descobrimos o valor exato de M, vamos substituir o M no valor das outras pastas que encontramos:
G = 1,60 + M => 1,60 + 3,20 = 4,80

P = 18 - 5M => 18 - 5(3,20) = 2,00

M = 3,20

A diferença entre o valor da pasta mais cara (G) e a pasta mais barata (M) é 2,80

ID

1169950

Banca

CETRO

Órgão

CHS

Ano

2014

Provas

CETRO - 2014 - CHS - Enfermeiro

Disciplina

Matemática

Assuntos

Fabinho e Zeca colecionam chaveiros com a imagem de jogadores de time de futebol. A coleção de Fabinho tem 11 vezes a quantia de chaveiros da coleção de Zeca. Se cada um deles ganhar 225 chaveiros, a coleção de Fabinho passará a ser o dobro da quantia de chaveiros da coleção de Zeca. Considerando esses dados, é correto afirmar que a coleção de Zeca tem

Alternativas

25 chaveiros.

30 chaveiros.

35 chaveiros.

40 chaveiros.

45 chaveiros.

Comentários

Fabinho= 11X
Zeca= X

Fabinho= 11X + 225 = 2X
Zeca= X + 225

Fabinho= 11X + 225 = 2X => 225 = 2X - 11X => 225 = 9X => X=225/9 => X=25

REsposta: 25
Primeira informação Fabinho é onze vezes zeca: F=11×Z
segunda informação se cada um deles ganhar 225 chaveiros, a coleção de Fabinho terá o dobro da coleção de Zeca:
F+225=2×(Z×225), tá formada a equação, agora só substituir a letra F da segunda equação pela pelo valor da primeira equação, F equivale a 11×Z:
F+225=2×(Z+225)
11×Z+225=2Z+450
11Z-2Z=450-225
9Z=225
Z=225/9
Z=25
Gabarito:A
Inicialmente,
F = 11Z
"Se cada um deles ganhar 225 chaveiros, a coleção de Fabinho passará a ser o dobro da quantia de chaveiros da coleção de Zeca."
F + 225 = 2(Z + 225)
F + 225 = 2Z + 450
11Z - 2Z = 450 - 225
9Z = 225
Z = 25
GABARITO: LETRA A

ID

1170643

Banca

FAFIPA

Órgão

PM-PR

Ano

2013

Provas

FAFIPA - 2013 - PM-PR - Soldado Bombeiro Militar

Disciplina

Matemática

Assuntos

Um artesão utiliza pernas idênticas de madeira para construir bancos e mesas. As mesas têm 3 pernas e os bancos, 4 pernas. Na última remessa de encomenda, ele utilizou 75 pernas de madeira para construir os bancos e as mesas. Sabendo-se que a quantidade de bancos construídos supera em 3 a quantidade de mesas construídas, a quantidade de bancos construídos foi

Alternativas

12.

15.

18.

Comentários

12 x 4= 48
9 x 3= 27
= 75

utiliza as as respostas
M (mesas) B (bancos) X é o numero de pernas

M=3x
B=4.(x+3)

3x+4(x+3)=75
3x+4x+12=75
7x=75-12
7x=63
x=63/7
x=9

Descobrindo o x, basta colocar na formula.

B=4.(x+3)
B=4(9+3)
B=36+12
B=48

Agora nós descobrimos que 48 é o numero de pernas dos bancos. Depois de descobrir isso, basta apenas dividir
o numero de pernas por 4 que é o numero de pernas que cada banco tem.

48/4 = 12

12 é o número bancos
Considerando que:
Bancos = x
Mesas = y
Pernas de bancos = 4x
Pernas de mesa = 3y
E que a quantidade de bancos construídos supera em 3 a quantidade de mesas construídas: x = y + 3

Podemos formar a seguinte equação:
Pernas de banco + pernas de mesa = 75 pernas
4x + 3y = 75
4 (y+3) + 3y = 75
y = 9 (quantidade de mesas)

Quantidade de bancos:
x = y +3
x = 9+3
x = 12

ID

1174858

Banca

COPESE - UFT

Órgão

Prefeitura de Palmas - TO

Ano

2013

Provas

COPESE - UFT - 2013 - Prefeitura de Palmas - TO - Agente Administrativo Educacional

Disciplina

Matemática

Assuntos

Um número multiplicado por 7 e somado com 5 é igual a 40. Que número é esse?

Alternativas

Comentários

7 * x + 5 = 40
7x + 5 = 40
7x= 40-5
7x= 35
x= 35/7
x=5
LETRA C

ID

1174861

Banca

COPESE - UFT

Órgão

Prefeitura de Palmas - TO

Ano

2013

Provas

COPESE - UFT - 2013 - Prefeitura de Palmas - TO - Agente Administrativo Educacional

Disciplina

Matemática

Assuntos

Maria comprou 2 anéis e 1 colar, pagando R$ 150,00 pelas 3 jóias. Sabendo que o valor do colar foi de R$ 80,00 e que os anéis têm o mesmo preço. Quanto custou cada anel?

Alternativas

R$ 20,00

R$ 35,00

R$ 45,00

R$ 70,00

Comentários

Gabarito B

I. 2A + C = 150

II. C = 80

2A + 80 = 150

2A = 70

A = 35

ID

1175041

Banca

COPESE - UFT

Órgão

Prefeitura de Palmas - TO

Ano

2013

Provas

COPESE - UFT - 2013 - Prefeitura de Palmas - TO - Técnico Administrativo Educacional

Disciplina

Matemática

Assuntos

Num determinado estacionamento da cidade de Palmas há vagas para carros e motos. Durante uma ronda dos agentes de trânsito, foi observado que o número total de rodas nesse estacionamento era de 124 (desconsiderando os estepes dos veículos). Sabendo que haviam 12 motos no estacionamento naquele momento, é CORRETO afirmar que estavam estacionados:

Alternativas

19 carros

25 carros

38 carros

50 carros

Comentários

TOTAL de 124 rodas

12 motos = 24 rodas

restando 100 rodas / 4 rodas cada carro

25 carros

ID

1178539

Banca

VUNESP

Órgão

SAAE-SP

Ano

2014

Provas

Disciplina

Matemática

Assuntos

Três irmãos, André, Beto e Caio estão colaborando com a economia de água e por isso reduziram o tempo de duração de seus banhos, de modo que a soma do tempo dos três banhos juntos é 18 minutos. O tempo de duração do banho de Beto é a metade da soma dos tempos dos banhos de André e de Caio. Sabendo que o banho de Caio dura 1 minuto a menos que o de Beto, então a duração, em minutos, do banho de André é:

Alternativas

Comentários

A média de minutos no banho dos 3 é igual a = 18/3 = 6 min
Sabemos que B = A + C/2 ----- B = 6+6/2 = 6
Sabemos tbm que C = 1-B ----- C = 1-6 = 5
Então:
A = 7 +
B = 6 +
C = 5
Total = 18
Alt. D = 7
A-> André; B-> Beto; C-> Caio
Se:
(1) A + B + C = 18
(2) B = A + C / 2, Donde A + C = 2B
(3) C = B - 1
Então:
Substituindo (2) em (1) B + 2B = 18 <--> B = 6, Então C = 5
(1) A + 6 + 5 = 18 <--> A = 7
A + B + C = 18 => A + C = 18 - B (I)
B = A + C / 2 (II)
C = B - 1 (III)

(I) em (II): B = 18 - B / 2 => 2B = 18 - B => 3B = 18 => B = 6
(II) em (III): C = 6 - 1 => C = 5
(II) e (III) em (I): A + 6 + 5 = 18 => A + 11 = 18 => A = 18 - 11 => A = 7

Alt. D = 7
b= a+c/2 ou a= 2b - c

2b - c + b + c = 18 (a + b + c)

b= 6

então c = 5 (b=c - 1)

faltam 7 para 18
Vamos chamar de A = André, B = Beto e C = Caio. Montando as equações de acordo com s dados do enunciado:

A + B + C = 18 (1)

C = B - 1

B = (A + C) /2 → B = (A + B - 1) / 2 → B = A - 1

Substituindo na equação (1):

A + A – 1 + A – 2 = 18

3A = 21

A = 7

Letra D.
Tempo do banho do André = A
Tempo do banho do Beto = B
Tempo do banho do Caio = C

Sabe-se que o banho dos 3 juntos é de 18 minutos, portanto... A + B + C = 18

O enunciado diz : "tempo de duração do banho de Beto é a metade da soma dos tempos dos banhos de André e de Caio",
portanto...B = A + C
2

E, por fim, o enunciado ainda diz: "o banho de Caio dura 1 minuto a menos que o de Beto", portanto... C = B - 1

=> Temos 3 incógnitas e 3 fórmulas:

(I) A + B + C = 18

(II) B = A + C
2

(III) C = B - 1

Multiplicando em X na equação II, temos: A + C = 2B.
A equação II, pode ser substituída na equação I e assim teremos: 2B + B = 18 => 3B = 18 => B = 6 minutos
Já que B = 6 min, então, podemos substituir na equação III, e teremos C = B -1 => C = 6 - 1 =>C = 5 minutos
Substituindo B = 6 e C = 5 na equação I, temos: A + 6 + 5 = 18 => A + 11 =18 => A = 18 - 11 => A = 7 minutos e essa é a resposta do exercício !!!
Pela lógica:

18 : 3 = 6 (média aritimética)

a = 6
b = 6
c = 6

c = b - 1 -> c = 5

se C é 5, logo B é 6 e esse 1 minuto que tirei do C, só sobrou o A para receber

a = 7
b = 6
c = 5

tirando a prova real :

b = a + c : 2
b = 12 : 2 = 6 (certinho)

Alternativa D

Bom estudo a todos e NAMASTÊ
andré + beto + caio = 18
beto = 12/2 = 6
caio = 6 - 1 = 5
andré = 18 - 6 - 5 = 7
A= ANDRÉ
B= BETO
C= CAIO

A+B+C = 18/3 = 6 (MEDIA)
Banho de Beto 12-6 = 6 minutos
Banho de André e Caio = 12 minutos
Banho de Caio, dura 1 minuto a menos que o de Beto = 6-1 = 5
Beto + Caio = 6 + 5 = 11
Banho de André = 18 - 11 = 7 minutos( altenativa D)
A + B + C = 18 minutos

A + C

B = ------------- ......vou deixar tudo em função de B!

2

2 B = A + C .... ou seja, A + C = 2B..... obs: >>> A + B + C = 18 minutos

agora é só substituir A + C por 2B >>>>> 2 B + B = 18

Logo!

3B = 18

B = 18/3

B = 6 ..... a questão disse que C é 1 minuto a menos que B, ou seja, C = 5

A = 7

B = 6

C = 5
2B = A + C

A + B + C = 18

2A + 2B + 2C = 36

2A +(A+C) + 2C = 36

A + C = 12 LOGO 2B = 12 LOGO B = 6

C = B - 1 LOGO C = 5

2B = A + C LOGO 12 = A + 5 LOGO A = 7

ID

1180627

Banca

VUNESP

Órgão

Câmara Municipal de São José dos Campos - SP

Ano

2014

Provas

VUNESP - 2014 - Câmara Municipal de São José dos Campos - SP - Técnico Legislativo

Disciplina

Matemática

Assuntos

Em um condomínio, a caixa d’água do bloco A contém 10 000 litros a mais de água do que a caixa d’água do bloco B. Foram transferidos 2 000 litros de água da caixa d’água do bloco A para a do bloco B, ficando o bloco A com o dobro de água armazenada em relação ao bloco B. Após a transferência, a diferença das reservas de água entre as caixas dos blocos A e B, em litros, vale

Alternativas

4 000.

4 500.

5 000.

5 500.

6 000.

Comentários

A B
Situação inicial: x+10.000 x
Transf. A para B: x+10.000-2000 x+2.000
''ficando o bloco A com o dobro de água armazenada em relação ao bloco B"
ou seja, A = 2B, portanto:
=> (x+10.000-2.000) = 2(x+2.000)
=> x + 8000 = 2x + 4000
=> 8000 - 4000 = 2x - x
=> 4000 = x
Portanto: A = x + 8000 = 4000 + 8000 => A= 12000
B = x + 2000 = 4000 + 2000 => B = 6000
A perguntar quer a difer: A-B = 12000 - 6000 = 6000 (Letra E)
Equação I - A=B+10.000 "a caixa d’água do bloco A contém 10 000 litros a mais de água do que a caixa d’água do bloco B"

Equação II - A-2000=2B+2.000 "Foram transferidos 2 000 litros de água da caixa d’água do bloco A para a do bloco B"

Equação III - A=2B "ficando o bloco A com o dobro de água armazenada em relação ao bloco B"

Substituindo I na II:

A-200=B+10000
B+10000-2000=2B+2000
1000-2000-2000=2B-B
10000-4000=B
B=6000

Substituição na III equação:
A=2B
A=2.6000
A=12000
Diferença:
12000-6000= 6000
usando o raciocinio
se a diferença é de 10000 litros entao
A perdendo-2000 litros a diferença cai para 8000 litros
B ganhando+2000 litros a diferença cai para 6000 fim
Bloco A = 10.000L a mais que o Bloco B.

Bloco A tranfere 2.000 L para o Boco B.

Bloco A fica com o dobro da capacidade do Bloco B.

Logo: Bloco A só pode ter 14.000 L - 2.000 L (transferência) = 12.000 L

Bloco B só pode ter inicialmente 4.000L + 2.000 L (recebidos) = 6.000L

Ou seja, a diferença entre A e B é de: 6.000L (Gabarito E)
A questão pode ser resolvida diretamente, tal qual a explicação do colega RODO >:), ou mediante o seguinte sistema de equações:

B + 10000 = A

A - 2000 = 2(B + 2000)

GAB: E
A = x + 10000
B = x

x + 10000 - 2000 = 2(x + 2000)
x + 8000 = 2x + 4000
8000 - 4000 = 2x - x
4000 = x

portanto, B = 4.000L, e A = x + 10000 = 4000 + 10000 = 14.000L (antes da transferência)

após a transferência,

A = 14000 - 2000 = 12.000 litros
B = 4000 + 2000 = 6.000 litros

Diferença: 12000 - 6000 = 6.000 litros (gabarito E)

ID

1187524

Banca

VUNESP

Órgão

TJ-SP

Ano

2013

Provas

VUNESP - 2013 - TJ-SP - Contador

Disciplina

Matemática

Assuntos

Um “cofrinho de economias” contém apenas x moedas de 10 centavos e y moedas de 25 centavos. Acrescentando-se nesse cofrinho mais x moedas de 50 centavos e y moedas de 1 real, o cofrinho ficará com 82 moedas, totalizando R$ 36,30. O total de dinheiro desse cofrinho, proveniente apenas das moedas de 25 centavos, é de

Alternativas

R$ 4,25.

R$ 4,50.

R$ 3,75.

R$ 4,00.

R$ 5,75.

Comentários

X=0,1
Y =0,25
Z= 0,50
W=1

X=z
Y=w

2x + 2y = 82
10x + 25y + 50z + 100w = 3630
não entendi? e a resposta? obrigada
x+y+x+y = 82
Retirando a forma decimal temos: 10x + 25y + 50x + 100y = 3630

I. x + y = 41 (a metade de 82)
II. 60x + 125y = 3630
multiplicando a equação I por (-60) para cancelar o x
- 60x - 60y = - 2460

125y - 60y = 3630 - 2460
65y = 1170
y = 1170 : 65 = y =18
x = 23

18 moedas de 25 centavos = R$ 4,50
a sacada é perceber que x + x + y + y = 82, então: 2x + 2y = 82
A. 2x + 2y = 82 => simplifica tudo por 2 => x+y = 41 => x=41-y
B. 10x + 25y + 50x + 100y = 3630 (tire da forma decimal para facilitar o cálculo) => 60x + 125y = 3630
Substituindo:
60 . (41-y) +125y = 3630
2460 - 60y + 125y = 3630
y=18
18 . 0,25 = 4,50
X=0,1
Y =0,25
X= 0,50
Y=1

x=41-y

10x + 25y + 50x + 100y = 3630

60 . (41-y) +125y = 3630

2460 - 60y + 125y = 3630

65y = 3630 - 2460

y=18

18 . 0,25 = 4,50

ID

1211962

Banca

FCC

Órgão

TRF - 4ª REGIÃO

Ano

2004

Provas

FCC - 2004 - TRF - 4ª REGIÃO - Técnico Judiciário - Área Administrativa

Disciplina

Matemática

Assuntos

Hoje, dois técnicos judiciários, Marilza e Ricardo, receberam 600 e 480 processos para arquivar, respectivamente. Se Marilza arquivar 20 processos por dia e Ricardo arquivar 12 por dia, a partir de quantos dias, contados de hoje, Marilza terá menos processos para arquivar do que Ricardo?

Alternativas

Comentários

M = 600 – 20d

R = 480 – 12d

600 – 20d = 480 – 12d

120 = 8d

d = 15

Decorridos 15 dias eles terão a mesma quantidade de processos para arquivar. Como Marilza aquiva mais processos por dia, então ela terá menos processos quando decorridos 16 dias.
Considerando x o número de processos feitos por dia

Tempo em que os dois arquivaram a mesma quantidade de processos:
480-12x = 600-20x
20x-12x = 600-480
8x = 120
x = 15

Em 15 dias arquivaram a mesma quantidade de processos, logo a partir do 16° dia Marilza terá arquivado mais processos do que Ricardo. Portanto alternativa C, 16 dias.
Considerando x o número de processos feitos por dia

Tempo em que os dois arquivaram a mesma quantidade de processos:
480-12x = 600-20x
20x-12x = 600-480
8x = 120
x = 15

Em 15 dias arquivaram a mesma quantidade de processos, logo a partir do 16° dia Marilza terá arquivado mais processos do que Ricardo. Portanto alternativa C, 16 dias.

Continue usando...

O que está incluso

+ 2 Milhões de Questões organizadas por assunto
+ 100 Mil Provas de concursos/vestibulares/ENEM
+ 1 Milhão de Questões comentadas
Pague uma única vez e tenha acesso vitalício

Entrar com o Google

📋 PIX COPIA E COLA 📲 Compartilhar PIX via WhatsApp

SóProvas