-
O raciocínio do colega acima está correto, porém o enunciado da questão já fala quais colunas que devem ser levadas em consideração E EXCLUE A COLUNA ~P, ficando assim:
P Q ~Q ~P P--->Q (P--->Q) ^ (~Q) [(P--->Q) ^ (~Q)]--->(~P)
V V F F V F V
V F V F F F V
F V F V V F V
F F V V V V V
Assim, só aparece realmente o valor lógico F 10 vezes (em verde). Só aparece 12 vezes se levarmos em consideração a coluna ~P (em vermelho), mas repito, pretem atenção que no enunciado a banca não fala na coluna ~P.
Enfim, não sei qual o erro da questão.
Alguém pode ajudar?!
-
erro do QC, na prova o CESPE inclui a coluna do ~p também.
-
Obrigado Lindemberg!!!!
-
Fiquei na dúvida. É para contar com os dois F do ¬ p???
-
Questão da prova inclui o ~p, logo o valor lógico F aparece mais de 10 vezes, como mostram os colegas acima.
"44 Considere a tabela-verdade da proposição S que contenha
apenas as colunas relativas às proposições p, q, ~p, ~q, p?q,
(p?q)?(~q) e S. Nesse caso, é correto afirmar que nessa tabela
o valor lógico F aparece 10 vezes."
http://qcon-assets-production.s3.amazonaws.com/prova/arquivo_prova/23986/cespe-2011-tj-es-cargos-de-nivel-superior-conhecimentos-basicos-somente-para-os-cargos-3-4-5-e-17-prova.pdf
-
como vinha falado, se são apenas 3 proposições e máximo de linhas dessa tabela-verdade é 8
-
ainda sou leiga no assunto , mais gostei muito de resolver
-
Questão ambígua, pois a questão pede se o valor lógico aparece 10 vezes, e a resposta é sim. Mesmo que ela aparecesse 20 vezes, ela teria aparecido pelo menos 10 vezes. Ali não diz se o valor aparece SOMENTE 10 vezes, ou seja, nos induz a interpretar de mais de uma forma.
De qualquer forma, se desconsiderarmos a ambiguidade teríamos:
que "p e q" = 2^2 (ou seja, quatro linhas)
P Q ~P ~Q [ (P→Q) ∧ (~Q) ] S: [ (P→Q) ∧ (~Q) ]→(~P)
V V F F F V
V F F V F V
F V V F F V
F F V V V V
Aqui já da para ter uma base, pois sabemos que o conectivo "então" (--->) é FALSO sempre quando o antecedente é V e o consequente é F. Já da para fazer de cabeça que daria mais de 10. No caso que disseram ali, que no comando não inclui o ~p, trate de ler novamente, pois no anunciado diz claramente para incluir esse ~p.
-
Acredito que na questão nem precise montar tabela verdade,pois, ele pede o número de Fs que vão aparecer para a proposicão S que é representada por [(p-->q) ^ (~q)] --> ~p
Mas mesmo que todos os valores fossem F teríamos apenas 4 por termos apenas duas proposições simples que formam uma tabela com 4 linhas.
Abçs
-
Nas tabelas: P = FF; Q = FF; ~P = FF; Q = FF;
Na tabela: P-->Q = F;
Na tabela: P-->Q ^ (~Q) = FFF;
Na tabela: S ( que é [ (p→q) ∧ (~q) ]→(~p)]) = (Tautologia: não tem Falso).
Assim: Como o enunciado pede todas as tabelas temos 12 F's.
(P) + (Q) + (~P) + (~Q) + (P-->Q) + (P-->Q) ^ (~Q) + S = 12
2 + 2 + 2 + 2 + 1 + 3 + 0 = 13
-
isso ai está errado mesmo existem 12 F a questão está errada
-
Desgraçou, o meu deu 11 !! Questão do sujo essa
-
Gente pelo amor de Deus né nem precisa montar a tabela
por que a questão pedo o valor lógico de S então como só tem P e Q logo a tabela só tem 4 linhas logo será impossivel aparecer 10 F
-
Fazendo a Tabela-Verdade:
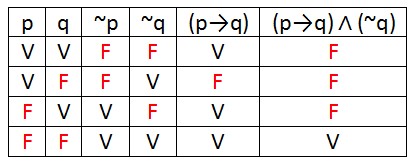
Logo, a quantidade de F que aparece na tabela acima é 12 vezes.
Resposta: Errado.
-
Pessoal, a questão diz que fazendo a tabela verdade para as proposições p, q , ~p,~q,p→q, (p→q)∧(~q), e S existirão 10 F, e isso está errado pois existem 12 F. Se existir qualquer quantidade de "F" diferente de 10, a resposta é "ERRADA", simples assim, não vamos complicar, temos que simplificar as coisas
-
Gente, o comentário do Ernesto Neves não tem nada a haver, ou só eu estou achando isso???
Ele está dizendo que é impossível ter 10 Fs, como é impossível se existem 12 nesta tabela!
Abraço a todos.
-
somente 4 linhas
-
DANILO DUTRA e ALCEMIR ALVES, o ERNESTO NEVES está certo. A proposição composta S "brinca" só com duas proposiçãos (a P e a Q). Sendo assim, a tabela-verdade da proposição S só apresentará 4 resultados. Para saber isso você deve pegar o número 2 e potencializar ele ao número de proposições. Nesse caso, como já disse, são apenas duas (a P e a Q), então 2 ao quadrado (igual a 4). Aí você já mata, porque o comando da questão afirmou que só de F tem 10. QUESTÃO MENTIROSA!
-
minha tabela deu 12 Fs, nao entendi esses que disseram 4 Fs
-
Considero tudo com "V":
[(V → V) ^ (~V)] → (~P)]
[V ^ F] → F
F → F
V
A proposíção é uma tautologia. Logo, é impossível ter qualquer "F"!
Questão ERRADA!
-
" o valor lógico F aparece 10 vezes" - ERRADO, aparece 12 vezes. É só fazer a tabela verdade e contar.
-
tem 2 letras... logo no maximo ai sem fazer tabela vai ter 4 F
gab errado
-
errado- o total é 12F, e nao 10
-
12x F.
-
FÉ!
-
Acertei a questão, embora tenha a interpretado errada. Ela não quer saber a quantidade de linhas, mas a aparição do valor lógico F na tabela verdade, com essa Cespe todo cuidado é pouco, pois uma interpretação equivocada você é penalizado duas vezes, errando uma questão simples dessa, perdendo outra. Vamos com atenção!
-
Na verdade o enunciado não deixa explícito se o que a banca quer é o valor lógico de S ou das suas proposições simples. Por isso, algumas pessoas aqui estão falando que se considerado o número total de linhas de S, no caso 4, seria inviável existir 10 valores falsos. Porém, também acredito que o enunciado esteja se referindo às proposições simples de S e, neste caso, nós chegamos em 12 valores lógicos falsos e 12 valores lógicos verdadeiros.
-
Pessoal está viajando bonito, a questão não pede o valor lógico de S, está faltando interpretação. O comando da questão é simples, montar uma tabela com as colunas referentes a p, q , ~p,~q,p→q, (p→q)∧(~q), e S, e contar quantos F aparecem em toda a tabela, e não na coluna S.
Portanto, a resolução correta é a dos colegas que chegaram a 12 F's.
-
Pessoal, por acaso tem alguma outra forma de fazer essa questão, sem fazer tabela verdade?
-
A tabela tem só qustro colunas,como que F vai aparecer 10*.
-
Na verdade, ao meu ver, a questão deveria ter como gabarito "C" ou ser anulada pois o valor "F" aparece 12 vezes, e então, também aparece 10 vezes, se tivesse falando "apenas 10 vezes" ai sim o gabarito seria "E". Esse tipo de questão não adianta tu saber a resposta, tem que adivinhar o que a banca que dizer.