- ID
- 4924
- Banca
- CESGRANRIO
- Órgão
- TCE-RO
- Ano
- 2007
- Provas
- Disciplina
- Raciocínio Lógico
- Assuntos
Sejam p e q proposições. Das alternativas abaixo, apenas uma é tautologia. Assinale-a.
Sejam p e q proposições. Das alternativas abaixo, apenas uma é tautologia. Assinale-a.
Chama-se tautologia à proposição composta que possui valor lógico verdadeiro, quaisquer que sejam os valores lógicos das proposições que a compõem. Sejam p e q proposições simples e ~p e ~q as suas respectivas negações. Em cada uma das alternativas abaixo, há uma proposição composta, formada por p e q. Qual corresponde a uma tautologia?
Assinale a opção verdadeira.
Julgue os itens seguintes relacionados à lógica proposicional.
Uma tautologia é uma proposição lógica composta que será verdadeira sempre que os valores lógicos das proposições simples que a compõem forem verdadeiros.
Quando Paulo estuda, ele é aprovado nos concursos em
que se inscreve. Como ele não estudou recentemente, não deve
ser aprovado neste concurso.
Em cada um dos itens a seguir, julgue se o argumento
apresentado tem estrutura lógica equivalente à do texto acima.
Sempre que Paulo insulta Maria, ela fica aborrecida. Como Paulo não insultou Maria recentemente, ela não deve estar aborrecida.
O perfil do profissional, nos tempos atuais, exige não só
o domínio de conhecimentos específicos mas também a
capacidade de adaptação rápida e assimilação de novas
informações de um mundo em constante transformação. Essa
constatação altera a dinâmica do processo ensino-aprendizagem
que privilegia o ensino de conteúdos, partindo do pressuposto de
que, quanto mais profundo e extenso for o conhecimento do aluno
sobre o conteúdo, mais preparado ele estará para prosseguir no
ensino universitário e, portanto, melhor será o seu desempenho
acadêmico ou profissional.
Em cada um dos itens a seguir, julgue se o trecho apresentado
constitui uma seqüência lógica das idéias apresentadas no texto
acima.
Dessa forma, torna-se responsabilidade da escola desenvolver nos alunos habilidades que os preparem a enfrentar situações inusitadas e a solucionar problemas para os quais não há resposta pronta.
O perfil do profissional, nos tempos atuais, exige não só
o domínio de conhecimentos específicos mas também a
capacidade de adaptação rápida e assimilação de novas
informações de um mundo em constante transformação. Essa
constatação altera a dinâmica do processo ensino-aprendizagem
que privilegia o ensino de conteúdos, partindo do pressuposto de
que, quanto mais profundo e extenso for o conhecimento do aluno
sobre o conteúdo, mais preparado ele estará para prosseguir no
ensino universitário e, portanto, melhor será o seu desempenho
acadêmico ou profissional.
Em cada um dos itens a seguir, julgue se o trecho apresentado
constitui uma seqüência lógica das idéias apresentadas no texto
acima.
É certo afirmar, portanto, que só tem competência aquele que constitui, articula e mobiliza valores, conhecimentos e habilidades para a resolução de problemas não só rotineiros mas também inusitados em seu campo de atuação. Assim, poucos agem eficazmente diante do inesperado e do inabitual, superando a experiência acumulada transformada em hábito e liberando-se para a criatividade e a atuação transformadora.
As proposições simples combinam-se com outras, ou são modificadas por alguns operadores, gerando novas sentenças chamadas moléculas. As moléculas em que os valores lógicos independem dos valores das proposições constituem uma
Na lógica proposicional, uma tautologia é uma fórmula proposicional que
Considere as proposições x e y e assinale a expressão que corresponde a uma tautologia.
Considere os símbolos e seus significados: ~ negação, ∧ - conjunção, ∨ - disjunção, ⊥ - contradição e Τ- tautologia. Sendo F e G proposições, marque a
expressão correta.
Considere os argumentos a seguir.
Argumento I: Se nevar então vai congelar. Não está nevando. Logo, não vai congelar.
Argumento II: Se nevar então vai congelar. Não está congelando. Logo, não vai nevar.
Assim, é correto concluir que
Considerando as proposições simples p e q e a proposição composta S: [ (p→q) ∧ (~q) ]→(~p), julgue os itens que se seguem.
Considere a tabela-verdade da proposição S que contenha apenas as colunas relativas às proposições p, q , ~p,~q,p→q, (p→q)∧(~q), e S.
Nesse caso, é correto afirmar que nessa tabela o valor lógico F aparece 10 vezes.
Considerando as proposições simples p e q e a proposição composta S: [ (p→q) ∧ (~q) ] →(~p), julgue os itens que se seguem.
A proposição S é uma tautologia.
A lógica é a “arte do bem pensar”, defendem algun autores. As fórmulas bem formadas da linguagem d lógica proposicional são construídas a partir de símbolos do alfabeto e de várias regras.
– Este animal é um coelho ou um cachorro.
– Não é um coelho.
– Logo, é um cachorro.
Acerca das proposições acima, assinale a opção correta.
Qual das proposições abaixo tem a mesma tabela verdade que a proposição: “ Se |a| < 3,
, então b ≤ 4 , onde a e b são números reais?
Se “A” é uma proposição verdadeira em relação à proposição “B”, é correto afirmar que
A contrapositiva de uma proposição condicional é uma tautologia.
PORQUE
A tabela verdade de uma proposição condicional é idêntica à de sua contrapositiva.
Analisando-se as afirmações acima, conclui-se que
A proposição “Carlito vai ao parque de diversões, ou não é verdade que Carlito vai ao parque de diversões, e Florinda não vai ao cinema” é
Considere o argumento seguinte:
Se o controle de tributos é eficiente e é exercida a repressão à sonegação fiscal, então a arrecadação aumenta. Ou as penalidades aos sonegadores não são aplicadas ou o controle de tributos é ineficiente. É exercida a repressão à sonegação fiscal. Logo, se as penalidades aos sonegadores são aplicadas, então a arrecadação aumenta.
Se para verificar a validade desse argumento for usada uma tabela-verdade, qual deverá ser o seu número de linhas?
Associe as explicações a seguir às respectivas fórmulas.
I - É uma tautologia
II - É satisfatível, mas não é uma tautologia
III - É insatisfatível
P= ∃x∃yA(x,y)∧¬∃xA(x,y)
Q= ∀x∀yA( x,y)∧¬∀x∀(x,y)
R= ∀x∀yA(x,y)-->∃x∀yA(x,y)
S= ∀x ∀y A(x,y) --> ∃x¬∀yA(x,y)
As associações corretas são:
Qual o numero de linhas de uma tabela verdade utilizada para determinar o valor lógico de uma proposição composta formada por 4 (quatro) proposições simples?
Em lógica, pelo princípio do terceiro excluído,
Considerando as proposições simples P, Q e R, julgue os próximos itens, acerca de tabelas-verdade e lógica proposicional.
A tabela-verdade da proposição (¬PVQ)→(R∧Q)V(¬R∧P) tem 8 linhas.
Considerando que P e Q sejam proposições simples, julgue o item
que se segue.
A proposição composta [P∧Q] ∨ [(-Q) → P] é uma tautologia.
A fim de convencer um cliente a contratar os serviços de cartão
pré-pago, o gerente de uma instituição financeira argumentou com
as seguintes proposições:
P1: Se uma pessoa não possui conta-corrente nem cartão pré-pago,
então ela efetua seus pagamentos em dinheiro.
P2: Se uma pessoa efetua seus pagamentos em dinheiro, então ela
carrega muito dinheiro no bolso.
P3: Se uma pessoa carrega muito dinheiro no bolso, então ela corre
o risco de ser assaltada.
P4: Se uma pessoa possui conta-corrente mas não possui cartão
pré-pago, então ela efetua seus pagamentos com débito em
conta.
P5: Se uma pessoa efetua seus pagamentos com débito em conta,
então ela corre o risco de perder o controle financeiro.
Com base na situação apresentada acima, julgue os itens
subsequentes.
Admitindo-se que seja verdadeira a proposição “uma pessoa efetua seus pagamentos em dinheiro”, é correto concluir que P1 será verdadeira independentemente do valor lógico das proposições “uma pessoa não possui conta-corrente” e “uma pessoa não possui cartão pré-pago”.
Ao analisar a documentação de um sistema de informação, um programador observa uma tabela-verdade T formada pelas proposições P,Q,R, X e Y.
Qual o número de linhas de T?
O enunciado que apresenta contradição, prejudicando a relação lógica entre as proposições, é:
Se Anamara é médica, então Angélica é médica. Se Anamara é arquiteta, então Angélica ou Andrea são médicas. Se Andrea é arquiteta, então Angélica é arquiteta. Se Andrea é médica, então Anamara é médica.
Considerando que as afirmações são verdadeiras, segue- se, portanto, que:
Se Ana é pianista, então Beatriz é violinista. Se Ana é violinista, então Beatriz é pianista. Se Ana é pianista, Denise é violinista. Se Ana é violinista, então Denise é pianista. Se Beatriz é violinista, então Denise é pianista. Sabendo-se que nenhuma delas toca mais de um instrumento, então Ana, Beatriz e Denise tocam, respectivamente:
Utilize o enunciado a seguir para responder às
questões 10 e 11.
Três funcionários do Tribunal de Contas do Estado
foram investigados pelo chefe imediato do setor em
que atuam acerca de uma consulta ilícita a um
relatório sob sigilo. O depoimento de cada um foi:
Ary: “Bruno não consultou o relatório e Clóvis
consultou";
Bruno: “Se Ary não consultou o relatório, Clóvis
também não consultou";
Clóvis: “Eu consultei o relatório, mas pelo menos
um dos outros dois não consultou".
Considere as proposições:
p: “Ary consultou o relatório";
q: “Bruno consultou o relatório";
r: “Clóvis consultou o relatório".
Assinale a alternativa que apresenta uma possível linguagem simbólica para o depoimento de Clóvis.
Sobre as tabelas de verdade dos conectivos de disjunção (inclusiva), conjunção e implicação (material), assinale a alter nativa correta.
Assinale qual é a contraditória do enunciado: Todo homem é mortal.
Um enunciado é uma tautologia quando não puder ser falso. Assinale a alternativa que contém um enunciado que é uma tautologia.
Enunciados contraditórios são enunciados que não podem nem ser ambos verdadeiros e nem ambos falsos. Nessas condições, assinale a alternativa que apresenta corretamente o enunciado que é o contraditório de “Todo homem é loiro”.
Um provérbio chinês diz que:
P1: Se o seu problema não tem solução, então não é preciso se
preocupar com ele, pois nada que você fizer o resolverá.
P2: Se o seu problema tem solução, então não é preciso se
preocupar com ele, pois ele logo se resolverá.
O número de linhas da tabela verdade correspondente à proposição P2 do texto apresentado é igual a
Um jovem, visando ganhar um novo smartphone no dia das crianças, apresentou à sua mãe a seguinte argumentação: “Mãe, se tenho 25 anos, moro com você e papai, dou despesas a vocês e dependo de mesada, então eu não ajo como um homem da minha idade. Se estou há 7 anos na faculdade e não tenho capacidade para assumir minhas responsabilidades, então não tenho um mínimo de maturidade. Se não ajo como um homem da minha idade, sou tratado como criança. Se não tenho um mínimo de maturidade, sou tratado como criança. Logo, se sou tratado como criança, mereço ganhar um novo smartphone no dia das crianças”.
Com base nessa argumentação, julgue os itens a seguir..
Considere as seguintes proposições: “Tenho 25 anos”, “Moro com você e papai”, “Dou despesas a vocês” e “Dependo de mesada”. Se alguma dessas proposições for falsa, também será falsa a proposição “Se tenho 25 anos, moro com você e papai, dou despesas a vocês e dependo de mesada, então eu não ajo como um homem da minha idade”.
Considerando que, P, Q e R sejam proposições conhecidas, julgue o próximo item.
A proposição [(P ∧ Q) -> R] ∨ R é uma tautologia, ou seja, ela é sempre verdadeira, independentemente dos valores lógicos de P, Q e R.
A proposição “João comprou um carro novo ou não é verdade que João comprou um carro novo e não fez a viagem de férias.” é :
Com base na proposição P: “Quando o cliente vai ao banco solicitar um empréstimo, ou ele aceita as regras ditadas pelo banco, ou ele não obtém o dinheiro”, julgue os itens que se seguem.
A negação da proposição “Ou o cliente aceita as regras ditadas pelo banco, ou o cliente não obtém o dinheiro” é logicamente equivalente a “O cliente aceita as regras ditadas pelo banco se, e somente se, o cliente não obtém o dinheiro”.
Com referência às proposições lógicas simples P, Q e R, julgue os próximos itens.
Se ¬R representa a negação de R, então as proposições P∨[¬(Q→R)] e (P∨Q)∧[P∨(¬R)] são equivalentes.
Se o valor lógico de uma proposição p é verdadeira e o valor lógico de uma proposição q é falsa, podemos afirmar que:
Considerando todas as possíveis valorações V ou F das proposições simples P e Q, a quantidade de valorações V na tabela-verdade da proposição (P∧Q)∨(~ Q ) → [ P∨(~ Q )] é igual.
Considerando que P e Q representem proposições conhecidas e que V e F representem, respectivamente, os valores verdadeiro e falso, julgue o próximo item.
A proposição [P V Q] → Q é uma tautologia.
Considerando que as letras maiúsculas P, Q e R representem proposições conhecidas, julgue os próximos itens.
Considerando-se as diferentes combinações de valorações verdadeiras ou falsas atribuídas às proposições P, Q e R, é correto concluir que as proposições Q➝P, ¬(P∧R) e Q∨R não podem ser simultaneamente verdadeiras.
Considere p e q fórmulas atômicas de uma linguagem L e v uma função de valoração na qual v (p) ≠ v (q).
Para tal, é necessário e suficiente que
Considerando os símbolos lógicos usuais e as representações das proposições lógicas por meio de letras maiúsculas, julgue os itens seguintes, relacionados à lógica proposicional.
A proposição [(P∧Q)∨R]∨Q⇔[P∨R∨Q]∧(R∨Q) é uma tautologia.
Considere a seguinte proposição:
“Ao participar de um concurso público, João será aprovado ou não será aprovado.”
Do ponto de vista lógico, a proposição acima é um exemplo de:
No que tange ao estudo do raciocínio lógico, é correto afirmar que contradição é uma proposição composta, na qual todos os valores lógicos da última coluna de sua tabela verdade são
O princípio da não contradição, inicialmente formulado por Aristóteles (384-322 a.C.), permanece como um dos sustentáculos da lógica clássica. Uma proposição composta é con- traditória quando.
José, Luís e Mário são funcionários públicos nas funções de auditor, analista e técnico, não necessariamente nessa ordem. Sabe-se que José não é analista, que o técnico será o primeiro dos três a se aposentar e que o analista se aposentará antes de Mário. Todo ano os três tiram um mês de férias e, no ano passado, no mesmo mês que José saiu de férias, ou Luís ou Mário também saiu.
Com base nessas informações, julgue os itens que se seguem.
Considerando-se as proposições “A: José tirou férias em janeiro de 2013”; “B: Luís tirou férias em janeiro de 2013”; e “C: Mário tirou férias em janeiro de 2013”, é correto afirmar que a proposição (A∧~C) →B não é uma tautologia, isto é, dependendo de A, B ou C serem verdadeiras ou falsas, ela pode ser verdadeira ou falsa.
Considerando a proposição P: “Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”, julgue os itens seguintes acerca da lógica sentencial.
Se a proposição “O candidato apresenta deficiências em língua portuguesa” for falsa, então a proposição P será verdadeira, independentemente dos valores lógicos das outras proposições simples que a constituem.
Se...então só será falso em Vera Fischer= Falso V--->F= F
a) o condidato é pós graduado
b) o condidato sabe falar inglês
c) o candidato apresenta deficiência em lingua portuguesa
d) deficiências não serão toleradas
( (A v B) ^ C) --> D
Segundo o enunciado, a proposição "C" é falsa, tornando todo o primeiro bloco ( (A v B) ^ C) ) FALSO por conta do conectivo E.
Matamos a questão aí, pois sobrou a condicional e sabemos que o único valor para negativar toda sentença seria VF. Como sabemos que a primeira é F podemos inferir que independente se a proposição "D" for verdadeiro ou falsa, a sentença toda estará correta.
É só seguir a tabela-verdade
A. B. A > B
V. V. V
V. F. F
F. V. V
F. F. V
OBS: lembrando que esta tabela funciona para a situação condicional (se A, então B)
lembrando que o "mas" foi utilizado com valor de conectivo "e".
Para poupar tempo não precisava nem fazer a tabela verdade.
Resolvi da seguinte forma:
P: (p v q ^ r) -> ~s
O candidato apresenta deficiências em língua portuguesa = r.
Se o "r" for falso, então teremos (p v q ^ r) = FALSO. Pois o "F" é quem manda na conjunção. Não importa os valores de "p" ou "q". Uma conjunção só será verdadeira quando todos os seus componentes forem também verdadeiros.
Logo: F -> V/F = V (sempre).
A condicional só será falsa quando o antecedente for "V" e o consequente for "F".
A= candidato for pós-graduado
B= Souber falar inglês
C= Apresentar deficiência em língua portuguesa
D= Deficiências não serão toleradas
mas = conectivo ^ (e/conjunção)
1º passo = montagem da proposição geral "P":
P = (A v B) ^ C→D
2º passo= já tendo "C" com o valor lógico Falso(F), atribuir o valor Verdade(V) à (AvB) e à "D"
temos:
V^F→V
F→V= Verdade
3° Passo= já tendo "C" com o valor lógico Falso(F), atribuir o valor Falso(F) à (AvB) e à "D"
temos:
F^F→F
F→F= Verdade
4° passo= já tendo "C" com o valor lógico Falso(F), atribuir o valor Falso(F) à (AvB) e o valor Verdade(V) à "D"temos:
F^F→V
F→V= Verdade
5°passo= já tendo "C" com o valor lógico Falso(F), atribuir o valor Verdade(V) à (AvB) e o valor Falso(F) à "D"
temos:
V^F→F*Lembrado que:
> Com o conectivo →(se...então), a proposição final "P" só será Falso, quando os valores das proposições seguirem a regra se(verdade), então(Falso).
> Com o conectivo ^ (e/conjunção), a proposição analisada só será Verdade(V) se os valores de ambas proposições forem Verdade(V).
Correto.
De forma simples:
Ficará assim
(PvQ^R)-->S
Uma vez que R é falso, sempre a proposição será verdadeira, dada a impossibilidade de haver o V-->F na condicional (Se, Então).
O "X" dessa questão está em entender o "MAS" com valor aditivo de "E".
Espero ter ajudado.
Eu fiquei na duvida em detalhe, acho que por isso que errei. Se a proposição “O candidato apresenta deficiências em língua portuguesa” for falsa, então a proposição P será verdadeira, independentemente dos valores lógicos das outras proposições SIMPLES que a constituem.
Não seria COMPOSTA não, porque existe a presença dos conectivos "e", "ou", alguém poderia me ajudar?
P: “Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”
A: o candidato for pós-graduado ou souber falar inglês
B: mas apresentar deficiências em língua portuguesa
Se a proposição “O candidato apresenta deficiências em língua portuguesa” for falsa, então B = F.
Com B = F, de acordo com a tabela-verdade, a conjunção (A ^ B) será falsa se A for V ou F. Logo não fará diferença o valor lógico de A, a disjunção neste caso será sempre F.
Sendo assim, é sabido pela tabela-verdade da condicional, que quando o antecessor for F não importa o valor lógico do seu sucessor, a condicional será sempre V.
Pelo visto, para o Cespe esse tipo de expressão deve ser entendida pela ORDEM que está escrita como (AvB) ^ C --> D.
Se fosse (AvB^C) --> D, seria Errada a resposta, pois caberia V --> F (Com o A sendo VERDADEIRA), o que resultaria em FALSA.
Dada a impossibilidade do termo: "Se V então F" na condicional a resposta está correta.
"Nos processos seletivos" a banca acrescentou só para confundir o candidato, na verdade nossa proposição começa logo após a primeira vírgula, observe:
A = se o candidato for pós-graduado
B = souber falar inglês
C = apresentar deficiências em língua portuguesa
D = essas deficiências não serão toleradas
Nossa sentença ficará assim:
(A v B ^ C) ---> ~D = Se o candidato for pós graduado OU souber falar inglês E(MAS) apresentar deficiências em língua portuguesa,ENTÃO essas deficiências NÃO serão toleradas.
Em seguida ele pergunta se toda a proposição terá valor verdadeiro se o C = F, vejamos:
(A v B ^ C) ----> ~D
(V/F v V/F ^ F) ----> V/F = se vc observa verá que a primeira parte da proposição será "F" independentemente dos valores de A e B, e na condicional quando a primeira parte e FALSA a proposição será sempre VERDADEIRA, ou seja, ~D pode ser tanto FALSO como VERDADEIRO.
Pessoal, ajudem-me por favor:
Algumas pessoas montaram, simbolicamente, da seguinte forma:
(A v B) ^ C --> D
A partir daí tudo bem. A proposição dará verdadeira independente dos valores lógicos que complementam "C" tornando o item correto.
Mas eu montei da seguinte maneira:
A v (B ^ C) --> D
V v (V ^ F) -> F
V v F -> F
V -> F Logo, tonando a proposição "Falsa" e, assim, tornando o item errado.
Gostaria que alguém pudesse me esclarecer este detalhe da prioridade dos parênteses.
P: “Nos processos seletivos, se o candidato for pós-graduado ou souber
falar inglês, mas apresentar deficiências em língua portuguesa, essas
deficiências não serão toleradas”
A: o candidato for pós-graduado
B: o candidato souber falar inglês
C: o candidato apresentar deficiências em língua portuguesa
D: essas deficiências não serão toleradas
P: (A v B) ^ C → D
Questão 34: Se a proposição “O
candidato apresenta deficiências em língua portuguesa” for falsa, então a
proposição P será verdadeira, independentemente dos valores lógicos das
outras proposições simples que a constituem. (CORRETA).
A questão disse que se a proposição “O candidato apresenta deficiências
em língua portuguesa” for falsa, então a proposição P será verdadeira,
independentemente dos valores lógicos das outras proposições simples que
a constituem.
Eu representei essa proposição pela letra C:
C: o candidato apresentar deficiências em língua portuguesa
P: (A v B) ^ C (F) → D
Sabemos que na conjunção, a proposição só será verdadeira se todas as
proposições simples que a compõe forem verdadeiras. Ou seja, V^V = V. Se
alguma preposição simples for F, a proposição composta será falsa.
P: (A v B) ^ C (F) → D
Se a proposição simples representada pela letra C for Falsa, a
proposição composta antes do conectivo → será falsa. Com isso, a
proposição P será verdadeira, pois no "Se, então", para ser falsa o
antecedente tem que ser Verdadeiro e o consequente falso. Na questão, o
antecedente é falso, logo, não tem como a proposição P ser falsa. Será
apenas verdadeira.
V→V= V
V→F= F
F→V= V
F→F= V
Se a proposição antecedente for Falsa, não tem como a proposição composta ser falsa. Ela tem que ser verdadeira.
Vamos reescrever a proposição P em forma de simbologia:
P: “Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”
A: o candidato for pós-graduado ou souber falar inglês
B: mas apresentar deficiências em língua portuguesa
C: essas deficiências não serão toleradas
Assim, P: (A ^ B) → C
Se a proposição “O candidato apresenta deficiências em língua portuguesa” for falsa, então B = F.
Com B = F, de acordo com a tabela-verdade, a conjunção (A ^ B) será falsa se A for V ou F. Logo não fará diferença o valor lógico de A, a disjunção neste caso será sempre F.
Sendo assim, é sabido pela tabela-verdade da condicional, que quando o antecessor for F não importa o valor lógico do seu sucessor, a condicional será sempre V.
Então concluímos que a proposição P será verdadeira, independentemente dos valores lógicos das outras proposições simples que a constituem.
RESPOSTA: CERTO
Certo.
(A v B ^ C ) --> D = V
(V v V ^ F ) ---> V = V
F --> V = V
Já sabendo que D é verdade, mata a questão fácil. Independente da 1º ser V ou F , se a 2ª for V a proposição é verdadeira.
Se fosse (AvB^C) --> D, seria Errada a resposta, pois caberia V --> F (Com o A sendo VERDADEIRA), o que resultaria em FALSA."
Verdade, você deve ter testado a expressão das duas formas: (AvB) ^ C --> D e Av(B^C) --> D
Muito boa a resposta do Ítalo, realmente a melhor. Obrigado
A minha dúvida é como alguns colegas encontraram direto a fórmula (que pareca mais fácil): P: (A ^ B) --> C
ou seja, sem o conectivo v (ou)....
Desculpem minha ignorância, mas tenho dificuldade para "fazer a leitura" do enunciado, estou aprendendo...
Obrigado.
Com todo respeito, mas a resposta do professor está um tanto que equivocada, pois o mesmo considera apenas 3 proposições simples, quando na verdade são 4.
A: o candidato for pós-graduado
B: o candidato souber falar inglês
C: o candidato apresentar deficiências em língua portuguesa
D: essas deficiências não serão toleradas
No mais, a resposta do Ítalo, logo abaixo, explica de forma categórica a questão.
"(CESPE – MDIC – 2014) Considerando que P seja a proposição 'A
Brasil Central é uma das ruas mais movimentadas do centro da cidade e lá
o preço dos aluguéis é alto, mas se o interessado der três passos,
alugará a pouca distância uma loja por um valor baixo', julgue os itens
subsecutivos, a respeito de lógica sentencial.
A proposição P pode ser expressa corretamente na forma Q∧R∧(S→T), em que Q, R, S e T representem proposições convenientemente escolhidas." GABARITO: CORRETO.
----------------------------------------------------------------------------------------------------------------------------
Um provérbio chinês diz que:
P1: Se o seu problema não tem solução, então não é preciso se preocupar com ele, pois nada que você fizer o resolverá.
(CESPE – SEGER/ES – 2013) Indicadas por P, Q e R, respectivamente, as proposições “Seu problema tem solução”, “Nada que você fizer resolverá seu problema” e “Não é preciso se preocupar com seu problema”, e indicados por “~” e “->”, respectivamente, os conectivos “não” e “se ..., então”, a proposição P1 pode ser corretamente representada, na linguagem lógico-simbólica, por
A) (~P) -> (R ->Q).
B) ((Q -> (~P)) -> R.
C) ((~P) -> Q) -> R. (Gabarito)
D) (~P) -> (Q -> R).
E) ((~P) -> R) -> Q.
Esse comentário do professor está errado...
Vejam o vídeo que gravei com a resolução dessa questão no link abaixo:
https://youtu.be/T056Lj_fy_4
Professor Ivan Chagas
MAS = conectivo "e"
Excelente questão :)
Estou me sentindo tão inteligente por responder essa questão sem ter nenhuma dúvida. rsrsrsr
Professor do QC montando a questão: P: (A ^ B) → C
A maioria dos alunos do QC montando a questão: P: ((A v B) ^) --> C
Prefiro ficar com os alunos, porque eu também cheguei a mesma conclusão. O gabarito dá no mesmo, mas ...
Sem falar que o comentário da questão por parte do professor deveria ser em vídeo aula.
G: CERTO. Pessoal, lembram que na matemática tem aquela ordem pra resolver a questão? ex (1+2*2) resolve 1º a multiplicação.
Nos conectivos tbm existe uma ordem: 1º ¬ , 2º ^ ou v na ordem que aparecerem, 3º v , 4º --> e 5º <-->
Na questão apareceu 1º o v, depois um ^ e por ultimo -->
vou chamar de C: Deficiências em língua portuguesa.
quando a questão diz: "essas deficiências não serão toleradas" esse "essas" retoma oq? As deficiências de língua portuguesa.
Logo: "essas deficiências não serão toleradas" = a ~C
(***SIM, A CESPE ADORA FAZER ISSO, MISTURAR LÍNGUA PORTUGUESA COM OUTRAS QUESTÃO.)
Montando fica: (AvB)^C --> ~C *** se o valor de C é F, substituindo fica:
(A v B)^F ---> V
V/F ^F ---> V
F ---> V
= V
NA CONDICIONAL, SE O ANTECEDENTE FOR FALSO, ENTÃO NUNCAAAAAAAAAAAAAAAA A PROPOSIÇÃO SERÁ FALSA. E SE O CONSEQUENTE FOR VERDADEIRO, ENTÃO NUNCAAAAAAAAAAAAAAAA A PROPOSIÇAÕ SERÁ FALSA. A QUESTÃO FOI BEM INTELIGENTE POIS, QUANDO FORMAMOS A PROPOSIÇÃO FICARÁ ASSIM :
A = o candidato for pós-graduado
B= souber falar inglês
C = apresentar deficiências em língua portuguesa
P: {(AvB)^C} ---> D
A QUESTÃO PEDE PARA COLOCARMOS O "C" COMO FALSO...E COMO NA CONJUNÇÃO ( sabemos que o conectivo mais forte entre as chaves é a conjunção ) SE UM TIVER FALSO, LOGO A PROPOSIÇÃO SERÁ FALSA...JUNTE AS PEÇAS...E VERÁ Q A PROPOSIÇÃO "P" SERÁ VERDADEIRA INDEPENDENTE DOS OUTROS VALORES.
VERDADEIRO ----> FALSO = FALSO.
GABARITO "CERTO"
Como gosto de construir a tabela-verdade (acho mais fácil do que gravar as equivalências), ai vai. Construa a tabela verdade e depois risque as linhas que contenham valor "falso" para a proposição " O candidato apresenta deficiência em língua portuguesa". As linhas que sobrarem comporão a tabela verdade para a proposição inicial "P". Analisando esta, veremos que teremos valores lógico "verdadeiros" para todas as linhas de "P", independente dos valores lógicos das outras proposições.
POLÍCIA FEDERAL!
Para resolver esta não perdi muito tempo, pensei da seguinte forma: Perceba que há 4 proposições simples ligadas entre elas por conectivos ^ ,v e -> ...“Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”"
P - se o candidato for pós-graduado
Q- souber falar inglês
R- apresentar deficiências em língua portuguesa
W- essas deficiências não serão toleradas
Montemos... (PvQ^R)->W
A questão diz que “O candidato apresenta deficiências em língua portuguesa”(R) é falsa, então a proposição P será verdadeira, independentemente dos valores lógicos das outras proposições simples que a constituem. SIM!!!
Basta testar.
(PvQ^R)->W
1º (F v F ^F)->F
F -> F = V
2º (V v F^F)-> V
F -> V= V
E assim sucessivamente..., pois como percebemos o conectivo que está ligando a proposição R é o ^ e como R é falsa, nunca poderá dar verdade no que consta entre parênteses e consequentemente na condicional nunca dará falso, pois a única possibilidade seria V->F = F
Flávio Batista compartilho do prazer em construir a tabela e fico mais seguro com o resultado.
A ordem é: (A ou B) ^ C --> D Sendo C falsa, a primeira parte da proposição será falsa, haja vista ter um conectivo ''e'' ligando "A ou B" a C. Como a condicional é falsa somente quando a primeira é verdadeira e a segunda é falsa, independentemente dos demais valores lógicos ela será sempre verdadeira. Gab: CERTO
(A ou B) e C -> D
C = F => O E só é verdadeiro se as 2 opções forem V, logo: a primeira parte da equação será sempre F !
Independente dos valores, a resposta final será sempre V:
F -> V = V
F -> F = V
Gabarito: CERTO
p : candidato apresenta deficiência -> p verdadeira
f -> f = v
f ->v = v
Proposição: (p v q ^ r) --> s . ''S'' pode ser tanto F quanto V. Resolvendo a primeira parte (p v q ^ r) NÃO SE CHEGA UM RESULTADO VERDADEIRO. Logo, em qualquer caso, essa proposição é verdadeira , já que não tem como dar Vera Fisher (V-->F)
(A ^B ) → C
F ou V com o F na conjunçao sera sempre F
logo F → F
ou ambos seriam verdadeiros
F → V
Eu acho que são 4 proposições [(PvQ)^R] -> S. O professor resolveu apenas com três proposições, não concordo.
Gabarito: CERTO
Concordo com o Bruno Magalhães! Em minha humilde opinião, temos 4 proposições simples:
A: O Candidato ser pós-graduado;
B: O Candidato saber falar inglês;
C: O Candidato apresentar deficiências em língua portuguesa;
D: Essas deficiências não serem toleradas.
Dessa maneira, a proposição composta P poderá ser representada da seguinte forma: P: (A v B) ^ C --> D
Se, conforme o enunciado aponta, a proposição C for falsa, então:
- o antecedente, representado por (A v B) ^ C, será sempre falso pois, independentemente do valor de A ou B, quando temos uma Conjunção (^), basta um falso para que a proposição composta seja FALSA;
- se o antecende for Falso (como já analisado), como temos uma CONDICIONAL, esta será sempre verdadeira, independentemente do valor do consequente.
Pra mim também são 4 proposições, concordo com a Flavia Jaine.
Pra mim, tb são 4 proprosições
A: O Candidato ser pós-graduado;
B: O Candidato saber falar inglês;
C: O Candidato apresentar deficiências em língua portuguesa;
D: Essas deficiências não serem toleradas
MINHA DÚVIDA:
Pelo que aprendi, resolvemos primeiro a conjunção (E), depois as disjunções.
Nessa caso, o que faz com que a disjunção fique entre parenteses é a vírgula?
(A v B) ^ C --> D
Eu errei a questão, pois pensei sem paranteses.
A v B ^ C --> D
Se fosse desta forma nãp seria verdadeira independentemente das outras. A
ALGUÉM PODE ME RESPONDER POR FAVOR??
Muita gente não está sabendo identificar o que a CESPE considera proposição simples e composta. Se não houver a repetição do sujeito + verbo, não haverá outra proposição, simples assim.
No caso da questão o ou não indica outra proprosição,apenas um mero complemento. Fiz a questão sem nem fazer tabela verdade.
A questão é um simples P ==> Q. ( p entao q)
Sendo P: "Se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa..." e Q: "essas deficiências não serão toleradas"
GABARITO CERTO
SINCERAMENTE QCONCURSO CONTRATE UM PROFESSOR QUE ENTENDA DO ASSUNTO POR FAVOR E QUE FAÇA AS RESOLUÇÕES EM VÍDEO.
OLHEM O QUE ELE DIZ SOBRE ESSA QUESTÃO
Vamos reescrever a proposição P em forma de simbologia:
P: “Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”
A: o candidato for pós-graduado ou souber falar inglês
B: mas apresentar deficiências em língua portuguesa
C: essas deficiências não serão toleradas
Assim, P: (A ^ B) → C
EM OUTRA QUESTÃO QUE É DO MESMO ENUNCIADO ELE SE CONTRADIZ, JÁ FALA QUE SÃO 4 PROPOSIÇÕES.
Separando a proposição P: “Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”, teremos:
A = o candidato for pós-graduado
B = souber falar inglês
C = apresentar deficiências em língua portuguesa
D = essas deficiências não serão toleradas
Sabemos que a quantidade de linhas associada a tabela verdade, respeita a seguinte fórmula, 2n, onde n representa o número de proposições, no nosso caso n = 4, logo: 24 = 16
CERTO
Conjunção ''E'' pode ser representada por sinônimos, que são : ''mas''. ''porém'', ''nem'' (nem= enão) e a própría VÍRGULA. Percebi que alguns concurseiros esqueceram deste conceito para identificar as preposições, bem como causando dúvidas.
Mão na massa!!!
P: “Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”
A: , se o candidato for pós-graduado CONDICIONAL -->
B , souber falar inglês CONDICIONAL -->
C , mas apresentar deficiências em língua portuguesa CONJUNÇÃO ^
D , essas deficiências não serão toleradas CONJUNÇÃO ^
Compreendendo a questão: Se a proposição “O candidato apresenta deficiências em língua portuguesa” for falsa, então a proposição P será verdadeira, independentemente dos valores lógicos das outras proposições simples que a constituem.
“O candidato apresenta deficiências em língua portuguesa”
A ------> B
No exemplo acima temos a união de A ----> B ''condicional'', partindo desse raciocínio, sabemos que, quando o antecessor for F não importa o valor lógico do seu sucessor, a condicional será sempre V. Ou seja, independe do valor da segunda.
''Que Deus esteja sempre com você, mas acima de tudo, que você esteja sempre com Deus. ''
Bons Estudos!!!
P: "Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas."
Legenda:
PG = se o candidato for pós-graduado
SFI = se o candidato souber falar inglês
ADLP = apresentar deficiências em língua portuguesa
DNST = deficiências não serão toleradas
Assim, vamos montar a preposição:
(PG v SFI) ^ ADLP --> DNST
A questão diz para considerar falsa "O candidato apresenta deficiências em língua portuguesa", (ADLP) então fica assim:
[(PG v SFI) ^ ADLP] --> DNST
F
Resolvendo isso, sabemos que essa preposição será verdadeira independente dos demais valores. Isso pq no conectivo "se...então" o resultado só será "falso" se os valores forem " V --> F " o que não é o caso da questão, pq a mesma poderá ser " F --> F" ou " F--> V ", e em qualquer um desses casos, o resultado será sempre " V ".
Comentário do professor ficou estranho.
Se (pós graduado ou fala inglês) e deficiências em Inglês ---> não haverá tolerância.
Como o que vem depois do "E" é falso, a primeira parte da proposição será sempre falsa (já que, para que a proposição "e" seja verdadeira, ambas partes devem ser verdadeiras).
Como a primeira parte da proposição 'SE' será SEMPRE falsa, independentemente do valor lógico da segunda parte, a proposição jamais poderá ser falsa, uma vez que, para tanto, a primeira parte deve ser verdadeira e a segunda falsa.
Cuidado! A forma como o professor do QC respondeu a questão está errada!
Vide o comentário do prof. Chagas: https://www.youtube.com/watch?v=T056Lj_fy_4&feature=youtu.be
NEGAÇÃO DA COMPOSTA ( Jhoni Zini )
https://youtu.be/tCwYy9zDWfc?list=PLzl2Ofs1h1zwZ46IcQ_8Vny6oGYSq9FYt
(PG v I) ^ DP ----> ~DT
F
Logo toda a primeira parte da proposição composta vai ser falsa, visto que o conectivo "e" exige as duas proposições verdadeiras para dar verdadeiro.
F ---> ?
Não é necessário saber qual será o valor lógico, pois o único caso em que a condicional vai dar falso é no Vera Fisher; nesse caso será verdadeiro.
GAB: CERTO
Conforme comentario do Givonilson: https://www.youtube.com/watch?v=T056Lj_fy_4&feature=youtu.be
Questão que em um primeiro momento você fica meio perdido, mas é bem simples. Veja:
Colocando na linguaguem proposicional
(PG v I) ^ P -> ~T
F (Sabendo-se que a proposição ligada ao conectivo ^ ("e"- exigente. só admite V V para ser Verdadeiro) é falsa, não há possibilidade do antecedente ser V para formar a única possibilidade de falsidade da condicional, qual seja V -> F = F )
A grande sacada da questão é saber que existe um ENTÃO antes da última preposição.(essas deficiências não serão toleradas).
A partir daí é so valorar que vai chegar á conclusão F> V. Flamengo na Frente, então é Verdadeiro
Só observar a tabela da condicional (se então)
Quando o antecedente for F, independente dos próximos valores o resultado será V.
Quando o consequente for V, independente dos valores do antecedente o resultado será V.
TABELA VERDADE:
Não entendi, fiz a tabela e P divido em A,B,C,D ficou= [(AvB)e~C]>D, nas linhas 4, 8 e 12 deram Falso. O q o enunciado quer?P ñ ficou verdadeira p qqr valor lógico.
Gabarito:Certo
Principais Regras:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação !!
Dada a proposição P= (AvB) ^ C -> D
A questão afirma que "C" é Falsa, então a Conjunção inteira (AvB) ^ C também é falsa.
Se a primeira parte é Falsa, pela regra da condicional (P->Q) a proposição só pode ser VERDADEIRA.
EX:
V->F = F
V->V = V
F->V = V
F->F = V
Gabarito: CERTO
“Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas"
Podemos simplificá-la assim:
G v i ^ ~P --> ~T
Agora é preciso tentar deixá-la falsa (V -->F), caso não seja possível será Tautologia
Lembrando que a ordem dos valores é na ordem em que aparecerem;
Professor do QC precisa ler os comentários para aprender com os alunos.
Considerando a proposição P: “Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”, julgue os itens seguintes acerca da lógica sentencial.
A tabela verdade associada à proposição P possui mais de 20 linhas
ITEM ERRADO
Nos processos seletivos, se o candidato for pós-graduado OU souber falar inglês, mas (E) apresentar deficiências em língua portuguesa, (então) essas deficiências não serão toleradas”,
A : se o candidato for pós-graduado
B: souber falar inglês
C: apresentar deficiências em língua portuguesa
D: essas deficiências não serão toleradas
[(AvB)^C]->D
Temos 4 proposições, então 2^4 = 16 linhas
Entendo que há a seguinte proposição composta: (p v q ) ^ r -> ~s. São 4 termos e para calcular a quantidade de linhas basta calcular 2 elevado à quantidade de termos que 4. Logo, serão 16 respostas ou linhas. Questão errada.
Para saber a quantidade de linhas, usa-se 2 elevado ao número de proposições ! Na questão são 4 proposições, ou seja, 2 elevado a 4 = 16 !! Mas, dava pra matar a questão mesmo sem saber a quantidade de proposições, pois n existe tabela com 20 linhas !!
(p v q) ^ r > t
2 elevado a 4 = 16 linhas
(A v B)^C-->D
2^4= 16
Numero de linhas = 2ª , sendo "a" o número de proposições simples
Logo, na questão seriam 4 proposições simples, ficando então: Nº de linhas = 2x2x2x2, logo Nº de linhas= 16
L = n ᵗ sendo n nº de valores, ou seja sempre 2 (V ou F) e t nº de termos que a proposição é formada, neste caso são 4.
Logo 2⁴.
4 frases: A: se o candidato for pós-graduado
B: souber falar inglês
C: mas apresentar deficiências em língua portuguesa
D: essas deficiências não serão toleradas
Vamos lá galera! costumo separar o contexto e dar nomes aos bois.
A=Nos processo seletivos.
B=O candidato for pós-graduado.
C=Souber falar inglês mas apresenta deficiências em língua portuguesa.
D=essas deficiências não serão toleradas.
Então temos (4) preposições sendo A,B,C,D, sendo assim multiplicaremos (Pº...fatores..n) resumindo e só elevar o números de preposições e multiplicar por (2)= então 2x2x2x2=16 linhas.....
2 ^ numero de proposições .........como nesse caso tem 4 proposições, seria 2x2x2x2= 16 linhas
A = o candidato for pós-graduado
B = souber falar inglês
C = apresentar deficiências em língua portuguesa
Acho que é suficiente saber que a frase trata-se de uma Sentença Aberta.
ser pós graduado - 1; falar inglês 2; deficiência em port. 3 e deficiência não será tolerada 4 ou seja 4 proposições, então teremos:
2^ ao número de proposições 2x2x2x2= 16.
Pessoal,se voces atentarem para o comentário da questão Q393380,o mesmo professor coloca para essa mesma proposição composta apenas 3 proposições simples.Acredito que sejam 4 proposições mesmo.
Errado.
Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, E apresentar deficiências em língua portuguesa, Então essas deficiências não serão toleradas.
(A v B ^ C) ---> D
2x2x2x2=16
2 elevado ao número de proposições , que no caso é 4, dá 16
2 elevado a quarta = 16
Joao Melo, também percebi que o professor considerou a proposição em uma questão com 3 proposições e em outra com 4...
Comentários:
Basta olhar as preposições e contar os CONECTIVOS. Esses aparecem na questão em forma de vocábulos (se, ou, mas, uma negação), logo teremos 2^4 = 16 linhas, ou seja, menos de 20 linhas.
Gabarito: ERRADO
(A v B ^ C) ---> D
Contamos o número de proposições e elevamos ao quadrado.
4x4=16 linhas
Deus ajuda quem estuda.
Leia a Bíblia.
essa explicação ficou meio controversa, pois na mesma questão anterior ele mesmo relata 3 conectivos. e creio que seja 3 mesmo! por que acho que a negação ta dento do contexto condicional, apenas parte do contexto do condicional, ele não ta negando nenhum conectivo, apenas o resultado da negação de V ou F( mudando o valor como é a função dela), e outro ponto a relatar, a negação ela não é conectivo, vendo isso, na soma 2n é o numero de preposições distintas mais os valores distintos, ou seja P,Q,R. NA TABELA VERDADE, REPITO, NA TABELA VERDADE, como a questão relata, a negação ela não conta na soma das linhas pois ela vem negando o conectivo.
AGORA se o enunciado pedisse à soma das preposições simples ou compostas seria outra coisa, pois iria contar a proposição com a negação a negando-a.
Marquei como não gostei ao comentário do professor e relatei a dúvida: Vejamos se teremos alguma resposta.
Numa questão anterior, tendo a mesma assertiva, "P: “Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”
o professor considerou uma proposição simples e em outra questão com a mesma assertiva, considerou como proposição composta, o que gerou uma grande dúvida, poderiam esclarecer, por favor?
Q393382
A = o candidato for pós-graduado
B = souber falar inglês
C = apresentar deficiências em língua portuguesa
D = essas deficiências não serão toleradas
Q393380
A: o candidato for pós-graduado ou souber falar inglês
B: mas apresentar deficiências em língua portuguesa
C: essas deficiências não serão toleradas
Assim, P: (A ^ B) → C
Separando a proposição P: “Nos processos seletivos, se o candidato for pós-graduado ou souber falar inglês, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”, teremos:
A = o candidato for pós-graduado
B = souber falar inglês
C = apresentar deficiências em língua portuguesa
D = essas deficiências não serão toleradas
Sabemos que a quantidade de linhas associada a tabela verdade, respeita a seguinte fórmula, 2n, onde n representa o número de proposições, no nosso caso n = 4, logo: 24 = 16.
Fonte:Vinicius Werneck (professor QC).
valeu xande pa finalmente aprendi como saber o numero de linhas!!
A = o candidato for pós-graduado
B = souber falar inglês
C = apresentar deficiências em língua portuguesa
D = essas deficiências não serão toleradas
São quatro proposições. 2 elevado a 4 = 16
2^4 (4 proposições simples) = 16 linhas.
Tenho essas e outras questões resolvidas em vídeo. Acesse http://www.tutorraciociniologico.com.br/
4 proposições, então terá 16 linhas.
Transformando em valores lógicos:
P v Q ^ R -> T
*Assim teremos 4 proposições e 16 linhas.
Em questão desse tipo, basta analisarmos a quantidade de proposições citadas e jamais esquecermos que o número de linhas da tabela-verdade sempre será a fatoração do número 2:
2^1= 2
2^2= 4
2^3= 8
2^4= 16
2^5= 32 etc
No entanto, só de sabermos esses valores, de cara já podemos responder como errada a questão, pois não existe tabela-verdade com 20 linhas.
Obs.: Colegas, me corrijam se estiver equivocada.
"Se você pode sonhar, você pode fazer."
Questão mamão com açucar
O NÚMERO DE LINHAS DE UMA TABELA VERDADE, VAI DEPENDER DO NÚMERO DE PROPOSIÇÃO SIMPLES QUE COMPÕE A PROPOSIÇÃO COMPOSTA.
É O CASO DA QUESTÃO....
FONTE : ALFA CONCURSOS
P ou Q e R então S.
16 linhas.
Apenas registrando minha indignação:
Como o mesmo professor, usando o mesmo enunciado (questões Q393380 e Q393382), pode chegar a conclusões diferentes?
Sendo mais específica: na questão Q393380, ele considera que P apresenta 3 proposições simples, enquanto na resolução da questão Q393382, ele considera que o mesmo P apresenta 4 proposições simples.
Minha indignação não está em o professor cometer um erro, até porque todos erram, mas em não ter a responsabilidade de retificar o erro frente aos milhares de alunos que, como eu, consideram suas explicações uma diretriz de seus estudos... :-(
Concordo com a Roberta Oliveira
Sou mais um q concorda com Roberta Oliveira.
Inclusive notifiquei a explicação do professor como NÃO GOSTEI e expliquei o motivo.
Não possui nem possibilidade de ter 20 linhas, de 2^4=16 2^5=32. Neste caso 4 proposições =16 linhas
errado -
(p\/q^r) -> s == 16 linhas
Roberta Oliveira
Gabrito ERRADO. Melhor explicação Danilo Capistrano.
Bons estudos!
JL.
16 linhas
2 elevado ao numero de proporcções.
Cuidado em, é 2 elevado ao número de proposições distintas.
Esse professor do QC tá meio doidinho!
Está se contradizendo na montagem da proposição na Q393382, pois disse que P: (A ^ B) → C
e agora na contagem do numero de linhas ,está dizendo que a premissa tem quatro proposições (A,B,C,D) que dá um numero de linhas igual a 16.
Me ajuda ai né!
Para achar o número de linhas de uma tabela-verdade utilizamos 2^n, em que "n" é o número de proposições simples.
Não é necessário nem ler a questão, 2 elevado a qualquer coisa NUNCA vai dar 20, independente do valor de n.
GAB: ERRADO
(A v B ^ C) --> D, LOGO, SÃO 16 LINHAS
O fino,
Sempre é necessário ler atentamente a questão, pois a questão afirma que a quantidade de linhas seria maior do que 20. Mesmo que 2 elevado a qualquer coisa nucna chegue a 20, poderia ser maior do que 20 e você erraria por não ler direito ;)
GABARITO ERRADO
Só irá ter 16 linhas, segue junto....
Vamos por partes, igual ao Jack Estripador...
O número de linhas da tabela-verdade é dada pela fórmula 2n (Dois elevado a N), onde:
2 --> é minha base (invariável), pois só teremos dois valores V e F
N --> número de proposições
E quantas proposições têm? 4 proposições, veja.
A : se o candidato for pós-graduado
B: souber falar inglês
C: apresentar deficiências em língua portuguesa
D: essas deficiências não serão toleradas
[(AvB)^C]->D
Temos 4 proposições, então 2^4 = 16 linhas
___________________________
O que queremos? Tomar posse.
E quando queremos? É irrelevante.
Flamengo na frente sempre Verdadeira
ESSA MESMO QUE NÃO SOUBESSE CONTAR AS PROPOSIÇÕES, ACERTARIA.
2^4= 16
2^5= 32
PRONTO, GAB= ERRADO
4² = 16, em que o 4 representa o número de proposições e o ² representa o número de valores lógicos, V ou F (só podem ser esses 2).
Se [(A ou B) e C] então D, lembrando que o "mas" equivale ao "e".
A : se o candidato for pós-graduado
B: souber falar inglês
C: apresentar deficiências em língua portuguesa
D: essas deficiências não serão toleradas
2^4 =16
Tem alguma regra para que "Nos processos seletivos" não seja considerada uma proposição?
Nos processos seletivo é apenas um aposto deslocado. Na ordem não deslocada seria
P: “ se o candidato for pós-graduado ou souber falar inglês, nos processos seletivos, mas apresentar deficiências em língua portuguesa, essas deficiências não serão toleradas”
Logo temos 2^4 = 16 < 20
Minha contribuição.
A v B ^ C -> D
2⁴ = 16 linhas
Abraço!!!
Costumo separar as proposições por verbos. Por ex: Nos processos seletivos, se o candidato for pós-graduado (1°), souber falar inglês (2º), mas apresentar deficiências em língua portuguesa (3º), essas deficiências não serão toleradas ( 4º). Logo, 2 x 2x 2x 2= 16 .
(A v B ^ C) ---> D = 4 proposições
2n= 2.2.2.2=16
A tabela verdade terá 16 linhas.
Gabarito:Errado
Principais Regras:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação !!
Dadas duas proposições simples, p e q, uma das leis de De Morgan perpassa a tautologia
[ ~ ( p ∧ q ) ] ↔ [ ( ~ p ) ∨ ( ~ q ) ]
Essa tautologia é logicamente equivalente à expressão.
Essa não tem jeito... vai ter que fazer a tabela verdade.
Resposta: letra A.
p q ¬p ¬q pvq ¬p^¬q ¬(¬p ^ ¬q) [¬(¬p ^ ¬q)] ↔ pvq
V V F F V F V V
V F F V V F V V
F V V F V F V V
F F V V F V F V
alguém sabe resolver de maneira mais fácil?
o Bruno inverteu os operadores lógicos???alguém põe exp!icar
Mto bom, Alisson. Valeu!
Seria difícil pq tem que analisar de um por um o bom é que você começa analisando a "A" e ela está correta rsrs.
[~ (( ~ p ) ∧ ( ~ q )) ] ↔ [ p ∨ q ]
expande o primeiro til
(pvq)<->(pvq)
Tautologia A implica A
Agora o que está alternativa tem haver com o enunciado:
[ ~ ( p ∧ q ) ] ↔ [ ( ~ p ) ∨ ( ~ q ) ]
ele nega as duas ue é a contrapositiva da bicondicional kk nem sabia que existia.
p^q<->p^q
a implica a
p->q^q->p
~q->~p^~p->~q
~q<->~p
~p<->~q
caraca existe mesmo a contra-positiva da bicondicional
Na bicodicional, para que assuma valor verdadeiro, ambas as premissas, antes e depois do conectivo principal, devem assumir, ou valor V, ou valor F, simultaneamente, ou seja, F+F= V; V+V= V
No caso em tela, ambas as premissas assumem valor V:
Para o conectivo (∧): v+v=V
Para o conectivo (∨): v+v=V
Para a bicondicional (↔):V+V=V
Portanto, trata-se de uma proposição lógica verdadeira.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------
Desta forma, das alternativas, a que apresenta valor lógico verdadeiro igual em ambas as premissas é a letra A, veja:
Sendo que:
Para a primeira premissa:
Portanto, para o conectivo (∧):
f+f= F
Para a segunda premissa:
Portanto, para o conectivo (∨) :
f+f= F
Para a bicondicional (↔):
F+F= V
---------------------------------------------------------------------------------------------------------------------------------------------------------
Logo, retomando o que foi dito no início, uma bicondicional pode assumir valor lógico Verdadeiro quando ambas as premissas assumirem, simultaneamente, valores lógicos V ou F.
Primeiro: o enunciado diz que a proposição dada é TAUTOLOGIA;
Segundo: ele quer saber qual das alternativas é equivalência da tautologia dada no enunciado, ou seja, ele quer saber qual das alternativas também é uma tautologia.
RESOLUÇÃO:
Bizu: o candidato deve saber o "uso dos parêntesis em lógica", para assim, eliminar o excesso de parêntesis existentes nas alternativas, para depois verificar se, entre as alternativas, existe alguma proposição tautológica.
Analisando a primeira alternativa "a": [~ (( ~ p ) ∧ ( ~ q )) ] ↔ [ p ∨ q ]
Elimina-se os parêntesis, temos: ( p ∧ q ) ↔ ( p v q )
Agora, verifique se tal proposição é uma tautologia: ( p ∧ q ) ↔ ( p v q ), pois, sabe-se que o conectivo "se somente se" somente é verdadeiro quando ambas as proposições forem todas v, ou todas f:
Primeiro testando as proposições p sendo v, e q sendo v:
( p ∧ q ) ↔ ( p v q )
v v v v
(v) (v)
Segundo testando as proposições p sendo f, e q sendo f:
( p ∧ q ) ↔ ( p v q )
f f f f
(f) (f)
Ambas as formas demonstram ser tautologias, logo gabarito letra A.
Considerando que P seja a proposição “Se os seres humanos soubessem se comportar, haveria menos conflitos entre os povos”, julgue os itens seguintes
Se a proposição “Os seres humanos sabem se comportar” for falsa, então a proposição P será verdadeira, independentemente do valor lógico da proposição “Há menos conflitos entre os povos”.
No conectivo "Se...então" só pode dar falso se as proposições simples forem V F....Caso contrário, sempre será V... Gabarito C
Item CERTO, pois:
“Se os seres humanos soubessem se comportar, (então) haveria menos conflitos entre os povos”
A -> B
A: Se os seres humanos soubessem se comportar (F)
B: (então) haveria menos conflitos entre os povos”
Ora, veja a tabela do se então:
A B A→B
V V V
V F F
F V V
F F V
Portanto, a proposição vai ser verdadeira independente do valor de B, já que A é Falto.
Se... então só é falso quando existe a Vera Fischer, V -> F = F.
Se... Então só é falso quando aparece a Vera Fischer: V, F = F.
p q - p p ---->q - p V q
v v f v v
v f f f f
f v v v v
f f v v v
p ---->q
f v/f
será verdadeiro, independentemente dos valores lógicos de q.
Proposições
V -> F = F
F-> V = V
F -> F = V
V -> V = V
Ou seja, se a primeira for falsa, a segunda poderá ser V ou F, mesmo assim o resultado será V.
Gabarito. Certo.
EQUIVALÊNCIAS DE PROPOSIÇÕES
P -> Q = ~P -> ~Q
P -> Q = ~P v Q
Equivalência de proposição Condicional (se-->então):
Regra do NEYMAR!! (P --> Q)
NEga a 1ª ~P
Mantém a 2ª Q
o Y do Neymar vira o (ou)(v)!! ~P ou Q = ~P v Q
Pois na CONDICIONAL se o antecedente for FALSO INDEPENDENTEMENTE DO VALOR DO CONSEQUENTE A PROPOSIÇÃO COMPOSTA SERÁ VERDADEIRA!!!
Questão repetida.
Resumo:
Se então: P->Q que só é falso se "P = F" & " Q = V"
Ele diz que:
"Os seres humanos sabem se comportar "(P) = FALSO já que a primeira proposição é falso logo podemos concluir que sempre será verdadeira.
Gabarito = Certo
A proposição "Se os seres humanos soubessem se comportar, haveria menos conflitos entre os povos" é uma condicional, se a 1° parte for falsa, pela tabela verdade sabemos que:
F → V = V e F → F = V
Logo, o valor lógico da 2° parte nesse caso não altera o valor lógico da proposição P.
A resposta é: Certo.
A proposição P é uma condicional q → p, que é logicamente equivalente a ~q v p.
Ou seja:
q → p = ~q v p = Os seres humanos não sabem se comportar ou haveria menos conflitos entre os povos".
A resposta é Certo.
É só seguir a tabela-verdade
A. B. A > B
V. V. V
V. F. F
F. V. V
F. F. V
OBS: lembrando que esta tabela funciona para a situação condicional (se A, então B)
Não conseguir entender este gabarito.
Os seres humanos sabem se comportar = F
Os seres humanos não sabem se comportar = V
ENTÃO
Se os seres humanos soubessem se comportar (ou seja, não sabem) = V
Preposição P ficaria assim: V > F ou V > V
Ou seja, gabarito ERRADO.
Alguém pode ajudar???
Thiago Ferreira eu não consegui entender seu raciocínio, mas vou tentar passar o meu entendimento da questão:
O conectivo usado na questão foi o "Se... então...." (O "então" foi substituído por uma vírgula o que também está correto).
Você resolve fácil essa questão se tiver o entendimento da tabela verdade: Se você verificar a tabela verdade notará que uma proposição com o conectivo "Se... então..." só será falsa se a 1º premissa for V e a segunda for F.
E como a questão diz que a 1º premissa " Os seres humanos sabem se comportar" é falsa então independente do valor da segunda premissa "Há menos conflitos entre os povos" ser V ou F essa proposição será verdadeira.
Lembre-se proposição com o conectivo "Se... então..." só tem valor falso se a 1º for V e a 2º for F.
Tentei colar uma tabela verdade aqui mas não deu muito certo hehehe
Mas espero ter ajudado!
Bons estudos!
GABARITO. CERTO.
P Q P->Q
V V V
V F F
F V V
F F V
FALSO SE ANTECEDENTE V E CONSEQUENTE F
Vera Fisher Fantastica
O resto será tudo verdadeiro...
Primeiro uma proposição é sentença declarativa afirmativa (expressão de uma linguagem) da qual tenha sentido afirmar que seja verdadeira ou que seja falsa.
Questão:
Considerando que P seja a proposição “Se os seres humanos soubessem se comportar, haveria menos conflitos entre os povos”, julgue os itens seguintes.
Se a proposição “Os seres humanos sabem se comportar” for falsa, então a proposição P será verdadeira, independentemente do valor lógico da proposição “Há menos conflitos entre os povos”.
Comentário:
Se P afirma que Se os seres humanos soubessem se comportar, haveria menos conflitos entre os povos (V), logo, é uma afirmativa verdadeira.
quando o autor da pergunta diz que "Os seres humanos sabem se comportar, ele está negando a afirmação que o mesmo fez na proposição P
Sabem ou não sabem se comportar | um ou outro.
Então se a proposição "Os seres humanos sabem se comportar" é ao contrário da P que ficaria "Os seres humanos não sabem se comportar, logo, temos uma verdade.
Resposta letra Certa
A →B = P
Dica: causaX efeito.
Condicional (se... então) [implicação]
A condicional é falsa se, e somente se, oprimeiro operando é verdadeiro e o segundo operando é falso.
A
B
A→B
V
V
V
V
F
F
F
V
V
F
F
V
A: “os seres humanos soubessem se comportar”. (A condicional é falsa se, e somente se,o primeiro operando é verdadeiro e o segundo operando é falso)
B: “haveria menos conflitos entre os povos”
Fibra e honra!
Certo.
Em uma vídeo-aula, o professor passou a seguinte dica: Lembre de Vera Fischer, essa mulher não existe! Enfim a proposição "Se...então" será falsa somente quando a primeira for V e a segunda for F. V--->F
POIS NA CONDICIONAL SÓ HAVERÁ UMA SITUAÇÃO EM QUE TEREMOS O VALOR LÓGICO FALSO:
V + F = F
NAS DEMAIS COMBINAÇÕES NA CONDICIONAL TEREMOS O RESULTADO "VERDADEIRO".
V + V = V
F + V = V
F + F = V
; ]
POIS NA CONDICIONAL SÓ HAVERÁ UMA SITUAÇÃO EM QUE TEREMOS O VALOR LÓGICO FALSO:
V + F = F
NAS DEMAIS COMBINAÇÕES NA CONDICIONAL TEREMOS O RESULTADO "VERDADEIRO".
V + V = V
F + V = V
F + F = V
; ]
Não entendi o que a questão queria.
Alguém pode ajudar?
- Inicialmente, iremos considerar proposições simples por letras minúsculas ( q, r, s ....) e proposições compostas por letras maiúsculas ( P, Q. ..)
P: Se os seres humanos soubessem se comportar, haveria menos conflitos entre os povos
q: os seres humanos sabem se comportar
r: há menos conflitos entre povos
P: q ---> r ( relação lógica representada pela condicional).
Vamos agora transcrever o enunciado e TRANSFORMÁ-LO para a "Linguagem lógica" obedecendo a configuração acima.
Os seres humanos sabem se comportar” for falsa, então a proposição P
será verdadeira, independentemente do valor lógico da proposição “Há
menos conflitos entre os povos”.
Se q é falsa, então a proposiçãoP será verdadeira, independentemente do valor lógico da proposição r.
Vamos ver se é verdade?
Construindo a tabela verdade da proposição composta "P"
q r q --->r
V V V
V F F
F V V
F F V
Vamos pensar amigos! Se "q" é falsa, 3º e 4º linha da tabela verdade, podemos com absoluta certeza INDEPENDENTEMENTE do valor lógico de "r" que a proposição resultante, ou seja, a proposição composta P será VERDADEIRA.
- Inicialmente, iremos considerar proposições simples por letras minúsculas ( q, r, s ....) e proposições compostas por letras maiúsculas ( P, Q. ..)
P: Se os seres humanos soubessem se comportar, haveria menos conflitos entre os povos
q: os seres humanos sabem se comportar
r: há menos conflitos entre povos
P: q ---> r ( relação lógica representada pela condicional).
Vamos agora transcrever o enunciado e TRANSFORMÁ-LO para a "Linguagem lógica" obedecendo a configuração acima.
Os seres humanos sabem se comportar” for falsa, então a proposição P será verdadeira, independentemente do valor lógico da proposição “Há menos conflitos entre os povos”.
Se q é falsa, então a proposição P será verdadeira, independentemente do valor lógico da proposição r.
Vamos ver se é verdade?
Construindo a tabela verdade da proposição composta "P"
q r q --->r
V V V
V F F
F V V
F F V
Vamos pensar amigos! Se "q" é falsa, 3º e 4º linha da tabela verdade, podemos com absoluta certeza INDEPENDENTEMENTE do valor lógico de "r" que a proposição resultante, ou seja, a proposição composta P será VERDADEIRA.
Seja a proposição P dada: “Se os seres humanos soubessem se comportar, haveria menos conflitos entre os povos”, logo, P é uma condicional que iremos separar da seguinte maneira:
q: os seres humanos soubessem se comportar
s: haveria menos conflitos entre os povos.
Assim P = q → s.
Se a proposição “Os seres humanos sabem se comportar” for falsa, pela tabela verdade da condicional, não importa o valor lógico de s, a proposição P sempre será verdade.
Resposta: CERTO.
GABARITO: CERTO
Resumindo:
As proposições equivalentes para p → q são:
~ q → ~ p
OU
~ p v qVAMO QUE VAMO, GALERA!!
Gab:Certo.
A condicional P----->Q sempre será verdadeira, exceto numa ocasião: quando a primeira for verdade e a segunda for falsa.
P: Os seres humanos soubessem se comportar
Q: haveria menos conflitos entre os povos
P (v) ----> Q (v)= V
P(f)----->Q (v) = V
P(f)-------->Q (f)= V
P(v)--------->Q(f)= F
Vejamos que nas primeiras três situações todas são verdadeiras. Apenas quando a primeira é verdade e a segunda for falsa é que a proposição será falsa.
Treine com exaustão até a perfeição.
Não é necessário analisar PROPOSIÇÃO PN! Trata-se de uma CONDICIONAL e está AFIRMANDO que a 1ª proposição é FALSA, então voce deve saber que na CONDICIONAL, se a PRIMEIRA for FALSA, sempre será VERDADEIRA!PRONTO. Nada de ANALISAR as proposições! Isso é CONCEITO, TABELA VERDADE NA CABEÇA!
Tabela Verdade da Proposição
P Q P--->Q
V V V
V F F
F V V
F F V
A questão fala da 3ª linha da tabela, então a proposição é verdadeira. CERTO.
Formas de equivalência do "Se...Então":
(P-->Q):
1º. P ^ ~Q
2º. ~P v Q
Eu só queria entender uma coisa:
“Se os seres humanos soubessem se comporta" é P, ok
"Os seres humanos NÃO sabem se comportar" é ~P por que?
Por acaso o soubessem é positivo, eles sabem se comportar?
O Cespe usa o NÃO acima de qualquer lógica, em circunstâncias normais, era presumível que "Soubessem" na verdade tem valor de "Não sabem"
O condicional ( --> ) se...,então. Só é falso quando temos Verá Fisher, ou seja, antecedente verdadeiro e consequente falso.
condicional (se p então q) = só será falsa quando a primeira for verdadeira e a segunda for falsa
(macete: Vasco na frente do Flamengo só pode ser Falso! )
p -->q
VV V
VF F
FV V
FF V
Na condicional
F --> F = V
F ---> V = V
A Comparação que a Fabiane fez me ajudou bastante com a Dúvida. Comparação do VASCO % FLAMENGO foi boa rsrs
p ---> q
só será F se a primeira for V e a segunda for F
para se lembrar (Vasco na frente do Flamengo! FALSO)
; )
Vai Fugir = Foge. outra dica para decorar a tabela verdade condicional.
P --> Q
negação¹ = P ^ ~Q
equivalência¹ = ~Q --> ~P
equivalência² = ~P v Q
A proposição ENTÃO somente será falsa se os conectivos forem respectivamente VF.
Dica : Vera Fischer é muito FALSA.
Adoro ver concorrente bitolado apenas ao VF=F!!! Mostra bem o nível...
Na proposição ele afirma o SE, ENTÃO, portanto se a primeira for F e a segunda é V, logo a resposta é V, INDEPENDENTE, da frase a seguir ser verdadeira ou não.
Na condicional, VF=F, já FV=V.
Outro macete no condicional além do Vera Fisher Falsa ( V F = F) é:
Vou Ficar Fera..... ai se vc quiser completar a frase... Nessa poha! rs
Certo.
F ---> ? = V
Questão simples , basta saber a regra dos conectivos.
Pessoal vamos praticar a humildade nos comentários, isso aqui é uma grande ferramenta de estudos, vários tipos de pessoas e necessidades, uns chegando, outros já em manutenção... Se pudermos agregar, façamos comentários construtivos.
Aos que tem dificuldades ou que estão chegando, indico os vídeos do Renato Oliveira que é do site mesmo, excelente didática.
Bons estudos!
Super útil sua dica!!! Valeu!
basta conhecer a regrinha dos conectivos, aí vai de boa
F Podemos colocar qq valor lógico de acordo com a tabela verdade, ou seja, V ou F.
Se os seres humanos soubessem se comportar, haveria menos conflitos entre os povos. = V
OBS: A questão menciona a possibilidade de usar as duas últimas linhas da tabela verdade para que a proposição seja V.
Tabela Verdade
A B | Y=A->B
V V | V
V F | F
F V | V
F F | V
O valor lógico do condicional só será falsa se a primeira for verdadeira e a segunda falsa. ao contrario sempre será verdadeira.
Só dá falso de V pra F(macete) Jairo Teixeira
bem explicado, Raquel! É isso aí!
Força guerreiros"
~H U => PO
F=>V = V
F=>F= V
Condicional
F-->V = V
F-->F = V
só um detalhe que os colegas aí em baixo não disseram... NÃO RESOLVA A TABELA VERDADE!! Pq até a pessoa entender que a questão se refere apenas às "ultimas duas linhas da tabela" que é um simples "F + F = v, F+ V= V" e que não é pra analisa-la por inteiro , ja era... erra a questão.
Na equivalência da condicional P --> Q, a regra troca pelo OU é: Nega a 1º, mantém a 2º ~ P v Q.
Foco nos estudos :)
O conectivo Se...então só será falso quando a primeira preposição for verdadeira ,e a segunda for falsa. Se não será verdadeira.
Tabela verdade do Se...então:
V ----> V = V
V ----> F = F
F ----> V = V
F ----> F = V
Deus é o nosso refúgio e fortaleza, socorro bem presente na angústia. Salmos 46:1
Leia a Bíblia.
Tabela verdade do Se...então:
V ----> V V
V ----> F F
F ----> V V
F ----> F V
Pode perceber que a primeira sendo falsa, o valor da segunda tanto faz, será verdadeira.
O princípio da sabedoria está em Deus, pois foi através dela que tudo se fez. Inclusive você.
Bons estudos a todos.
Vera Fischer é Falsa
Corretíssimo
Na condicional (Se... então ou "-->") só tem a possibilidade de o resultado ser F (falso), caso o antecessor seja V (verdadeiro)
Logo:
A = F --> V = V
A = F --> F = V
Essa aí é outra pegadinha. O cespe adora misturar as coisas. É só se manter fiel à definição de condicional pessoal. Se P for verdadeira, que no caso será a 2° proposição no exemplo, então não importa qual seja a 1° proposição. Exemplo. A Terra é azul (proposição) é verdadeira, independentemente de A, B C... qualquer proposição ser V ou F. A 2° proposição é independente e nenhuma outra proposição seja V ou F vai mudar isso.
Regra do "SE ENTÃO" para "OU" :
Nega a primeira e mantém a segunda.
Vasco na frente do Flamengo é falso!
V -> F = F
Só lembrar
V ----> F :::: F
Vera Fisher Fudida
A minha duvida ficou na seguinte situação: " se os seres humanos soubessem se comportar" não é uma negação? ou seja que eles não sabem se comportar. estou na dúvida.
SE ,ENTAO P->Q
SE os seres humanos não sabem se comportar, ENTAO haveria menos conflitos entre os povos”
GAB CORRETO
Vejam o vídeo que gravei com a resolução dessa questão no link abaixo:
https://youtu.be/2yI4rC8zreM
Professor Ivan Chagas
Vejam o vídeo que gravei com a resolução dessa questão no link abaixo:
https://youtu.be/VAMd8ebe96g
Professor Ivan Chagas
Eu entendi que se a proposição diz - "Se o seres humanos
soubessem se comportar", (é porque eles não sabem se comportar),
portanto a tornei verdadeira, importando sim no valor da proposição
seguinte, já que V que implica F é F. Quem puder ajudar nesse entendimento agradeço!
Isabela seu erro foi interpretar a proposição ''Se os seres humanos soubessem se comportar'' pelo ponto de vista da língua portuguesa na qual pelo tempo verbal de ''soubessem'' realmente poderia ser feita a sua inferência a respeito do sentido da proposição.Mas essa questão tem que ser analisada pelo ponto de vista da lógica formal,portanto se o enunciado da questão lhe pede para que seja feita a resolução da questão à partir da hipótese da primeira proposição simples ser falsa,esse deverá ser o seu ponto de partida,e partindo desse ponto teremos que : proposições com o operador lógico condicional (se...então) só serão falsas se a primeira proposição simples for Verdadeira e a segunda Falsa (V ---> F),ou como o mnemônico que eu aprendi diz : Só será falsa quando ''Vai à festa'' (V e depois F).
Espero poder ter ajudado.
Engraçado que questão fácil: Chove comentários! rsrsrs
Bazinga!!
A primeira premissa faz referencia de que ela e falsa e seu resultado verdadeiro: F ----> (??)= V
Onde a segunda premissa não interfere no resultado(??), pois esta poderá ser verdadeira como falsa, que mesmo assim manterá Verdadeira. No conectivo Se então so sera Falso se a primeira premissa for verdadeira e a segunda falsa. Exº V--->F = F
PORTANTO
F ----> (??)= V
F ----> (V,F)= V
Condicional: só da F de V pra F.
Quando nos deparamos com uma condicional, temos que lembrar que só V + F é F.
Se a primeira parte da proposição for falsa, o resultado final é verdadeiro.
Condicional:
V + V = V
V + F = F
F + V = V
F + F = V
Boa sorte!
É a negação da negação!
CERTO
No -> (se...então) só dá FALSO de V ->F, então sendo a 1ª proposição falsa independente do valor lógico da 2ª proposição o valor lógico final será VERDADEIRO.
Na condicional, se a primeira foi Falsa, independente do valor da segunda, a proposição sempre sera verdadeira.
V + F = F
no condicional independente de outra proposição V + F = FALSO
Certa
P: x -> y (x e y foram convenientemente escolhidos)
P: F -> y
P: V (qualquer valor na tabela do "Se...Então..." que comece com "F" terá o resultado final sendo "V")
x y x->y
V V V
V F F
F V V
F F V
Definitivamente a expressão "se eu enxergasse" não é igual a "eu enxergo". Uma é a negação da outra. O tempo verbal faz toda a diferença. Vai entender o cespe.
Certa.
A condicional só tem a possibilidade de ser falsa se a primeira for verdadeira.
EQUIVALÊNCIA
P->Q ¬PVQ
P->Q ¬Q->¬P
TOMA !
Que venha assim na prova. Amém!
Aos que se gabam por terem acertado e dizem que a questão foi fácil.. eu lhes pergunto:
Desde quando "sabem" é a mesma coisa que "se soubessem"???
"Se soubessem" passa a ideia de que não sabem, portanto seria o inverso de "sabem", abrindo espaço para que a questão esteja ERRADA!
E mesmo que não passasse ideia de negação, as duas orações têm sentido diferente, o que inviabiliza a resposta..
MAS, para a Cespe e para a maioria, tempos verbais diferentes não geram alteração de sentido...é candidatos...as questões de português aguardam por vcs rsrs..
Tão fácil que errei!! Que raiva!!
concordo com Toni Lee!!! Saber e soubessem passam ideias diferentes! AAAAAh neeeeeeem...
Na proposição se etnaão somente Vera Fischer é falsa.
Questão fácil pega bobos desprevinidos!!
Sobre o comentário do amigo Toni
A diferença não seria sanada ao trazer o verbo haver para o mesmo tempo?
Certa.
A condicional só tem a possibilidade de ser falsa se a primeira for verdadeira.
Na condicional se a anterior for F e a posterior for V ou F a proposição será sempre verdadeira. Certíssimo!!!
P->Q
F->V =V
F->F =V
Vai Fugir? Foge!
CERTO.
Para a proposição condicional ser verdadeira, o antecedente necessariamente terá que ser verdadeiro: V-->F= F
Condicional:
VeraFisheréFALSA
VascoeFlamentosempredáFLAMENGO.
Embora seja vascaíno, rss, na prova tudo é válido.
GAB CERTO
Um maçete legal que me fez gravar:
O marido disse a mulher: SE CHOVER, ENTÃO TE BUSCO.
Não choveu( F), não buscou (F) = esposa não vai brigar (V)
não choveu(F), buscou(V) = esposa não vai brigar (V)
choveu (V), buscou ( V)= eposa não vai brigar (V)
choveu(V), não buscou (F)= VAI TER BRIGA (F)
CERTO
SE os seres humanos sabem se comportar, Então há menos conflitos entre os povos.
F -> V/F indenpendente da segunda parte ser V ou F a proposição será Verdadeira
V->F é a única condição da bicondicional ser Falsa!!!
Aí, galera! Condicional!
Se caso aparecer VERA FISHER (É FALSO)
BASTA APLICAR O SEGUINTE:
SE O VALOR DA PRIMEIRA PROPOSIÇÃO É F
O CONECTIVO É ( SE ENTAO), ENTAO: F se entao F = V
F se entao V = V.
PARA QUALQUER VALOR QUE SE DER A SEGUNDA PROPOSIÇAO O
RESULTADO SERÁ SEMPRE VERDADEIRO.
sim, considerando a proporsição P.
P= A -> B
P = F -> ? V
Poís será falso somente quando houver V -> F.
CERTO - Por que?
Porque, a única possível condição para que o "se ...então", condicional, ser falsa é "Vera Fisher" é falsa, lembram-se? Sendo a proposição composta condicional, NÃO comutativa, ou seja, importa o onde está o valor lógico, qualquer que seja o valor lógico da segunda proposição, será sempre Verdadeiro, porque na questão afirma-se que a primeira é falsa.
Conectivo SE, ENTÃO só ficará falso quando for V --> F
A questão Descreve a seguinte Situação
F >>>>>> F
F >>>>>>V
Qualquer das duas são verdadeiras
Bom dia,
No SE ENTÃO a única possibilidade de termos uma valor FALTO é a primeira proposição (p) ser V e a segunda (q) ser F, como a questão propõe atribuir (p) como F, então INDEPENDENTEMENTE do valor de (q) sempre teremos uma sentença VERDADEIRA;
Bons estudos
115 comentários deu até medo de marcar, simples demais pra ser vdd
Fica a dúvida de /\ ou ->
Ga Certa
Flamengo na frente já é verdade.
Flamengo na frente sempre Verdadeira
Li a questão, vi a quantidade de comentários e imaginei será que essa questão tem pegadinha.... (ou será que ela tem risco remoto de estar totalmente errada).. rsrsrs
EM OUTRAS PALAVRAS ELA PERGUNTOU, SE FOR FALSA A PRIMEIRA, TEM ALGUMA POSSIBILIDADE DE SER FALSA A FRASE TODA?
F -> V = VERDADEIRA
GABARITO= CERTO.
DA MEDO DE MARCAR, MAS ESTA CORRETA.
A proposição "Se os seres humanos soubessem se comportar, haveria menos conflitos entre os povos" é uma condicional, se a 1° parte for falsa, pela tabela verdade sabemos que:
F → V = V e F → F = V
Logo, o valor lógico da 2° parte nesse caso não altera o valor lógico da proposição P.
A resposta é: Certo.
Se os seres humanos soubessem se comportar, haveria menos conflitos entre os povos”
“Os seres humanos sabem se comportar”
Soubessem não significa "que nao sabem"?
é se "sabem" e falso "não sabem" seria verdadeiro, Então dependeria sim do valo da outra preposição.
Fiquei na duvida aqui.
F → V = V
F → F = V
Gaba: C
Só observar a tabela da condicional (se então)
Quando o antecedente for F, independente dos próximos valores o resultado será V.
Quando o consequente for V, independente dos valores do antecedente o resultado será V.
TABELA VERDADE:
Se a proposição [Y] “Os seres humanos sabem se comportar” for falsa, então a proposição P será verdadeira, independentemente do valor lógico da proposição [X] “Há menos conflitos entre os povos”.
Certo, perceba que independente do valor da proposição [X] o resultado da proposição P permanecerá V.
Y -> X
F -> V = V
F -> F = V
Dê o somatório dos itens verdadeiros:
(1) Uma sentença composta é chamada Tautologia quando seu valor lógico for sempre verdade, independentemente dos valores lógicos das sentenças simples que a compõem.
(2) Todas as sentenças contraditórias são equivalentes.
(4) A sentença ~ P ∧ P é uma tautologia.
(8) Existem duas sentenças tautológicas que não são equivalentes.
Gabarito A
Apenas os itens (1) e (2) são corretos.
Thiago Trigo, só uma correção:
Contradição --> a proposição composta não é tautologia, apresenta valor lógico sempre F
;)
Resposta; Letra A
1 E 2 estão corretas.
o certo da tabela verdade é o seguinte:
p ~p p^ ~p
V F F
F V F
São só duas linhas, e não quatro como o colega thiago colocou, pois é uma proposição só, se fossem p e q, por exemplo, seria quatro linhas!!!!
Bons Estudos galera!!! força e fé!!!
De acordo com a teoria sobre tautologias, a opção (1) está correta, pois há certas proposições compostas, chamadas de tautologias, que assumem valores lógicos V em todos os casos possíveis.
Para ser uma sentença contraditória, basta o resultado da mesma ser sempre F na tabela verdade, se outra sentença também for contraditória ambas sejam equivalentes, pois possuem o mesmo resultado final em suas tabelas-verdades, logo a opção (2) está correta.
Para saber se a opção (4) está correta ou não, basta fazer a tabela-verdade, logo:
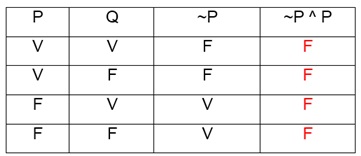
Logo temos uma Contradição, e não uma
tautologia, opção errada.
Duas sentenças tautológicas sempre serão equivalentes, pois possuem o mesmo resultado final em suas tabelas-verdades iguais, logo opção errada.
Assim, temos apenas duas opções corretas, a (1) e (2), somando ambas temos 1 + 2 = 3.
RESPOSTA: (A)
Por quê os comentários dos concurseiros são sempre melhores e claros que os do professor?
Raphael Rocha dos Santos deve ser porque ´´estamos com a mão na massa`` todos os dias estudando.
kkkkkk
e mais difícil do parece
Raphael Santos, também penso da mesma forma, os comentários dos concurseiros são mais claros e de fácil entendimento, acredito que seja por que são gente como a gente, explicam de uma forma simples.
Amigo Marcelo Mendes você tem que fazer tanto com V quanto com F não só de uma maneira mais para ter certeza das duas maneiras!
Tanto com V quanto com F
Questão muito inteligente.
ELE INVERTEU TENTANDO PEGAR O GUEIRO DESPREVINIDO. TAUTOLOGIA NA (4) É P v ~P
Cara, como que uma contradição com 4 linhas na tabela verdade pode ser equivalente a outra contradição com 8 linhas? Alguém me explica isso ai...
ALTERNATIVA A)
Questão comentada pelo Prof. Jhoni Zini no link abaixo a partir do minuto 37:43
https://www.youtube.com/watch?v=Bn3rIpyAnDM&t
SOMANDO TUDO DÁ 15.
ELIMINEI A 4= LOGO TUDO DA 11
A RESPOSTA PODE SER 11, 7 OU 3
NÃO PODE SER 7, POIS SOMANDO AS ALTERNATIVAS DA 11 (PASSA), SOMANDO DUAS DELAS DÁ MAIOR DE 7 OU MENOR DE 7.
A RESPOSTA PODE SER 3 OU 11
SEI QUE A 1 TÁ CERTO.
É A ULTIMA DA ERRADA.
LOGO SÓ RESTA A 3, POIS NÃO OUTRA ALTERNATIVA.
(1) Uma sentença composta é chamada Tautologia quando seu valor lógico for sempre verdade, independentemente dos valores lógicos das sentenças simples que a compõem. (CERTO)
Uma Proprosição Composta sempre terá valor Verdadeiro indepedente quais sejam os valores das proposições que as componham.
(2) Todas as sentenças contraditórias são equivalentes.
Certo. Todas as sentenças contraditórias tem o Valor F como resultado. Elas são o oposto da tautologia. Logo se temos 2 sentenças que são contraditórias implica dizer que elas terão o valor Falso como resultado e para o Lógica de Argumentação serão equivalentes.
(4) A sentença ~ P ∧ P é uma tautologia.
A sentença acima é uma contradição pois seu resultado será sempre falso. Pois o conectivo de adição para ser verdadeiro sempre precisa de 2 verdades.
(8) Existem duas sentenças tautológicas que não são equivalentes.
Se são tautológicas, sempre terão o valor Verdadeiro e sempre serão equivalentes.
Gabarito letra "A".
Um enunciado é uma tautologia quando não puder ser falso, um exemplo é:
GABARITO: E) Está fazendo sol ou não está fazendo sol.
A QUESTÃO SOLICITA O ITEM EM QUE TODOS OS VALORES LÓGICOS DA TABELA VERDADE SEJAM VERDADEIROS
=> UMA TAUTOLOGIA.
Está fazendo sol ou não está fazendo sol
--------------------------------------------------------------
P ¬ P = P v ¬ P
--------------------------------------------------------------
V F = V
F V = V
--------------------------------------------------------------
NA DISJUNÇÃO INCLUSIVA SÓ SERÁ FALSO EM UMA SITUAÇÃO:
OU => F + F = F
; ]
Gabarito. E.
______________________________________________
a)
P ^ Q
V F = F
______________________________________________
b)
P = V/F
______________________________________________
c)
P -> Q
V F = F
______________________________________________
d)
b)
P = ~V/~F
______________________________________________
e)
P v Q
V F = V
______________________________________________
A questão quer que achemos uma tautologia, ou seja, a proposição composta deve ter toda sua valoração "V"erdadeira.
Inicialmente, iremos considerar a proposição simples por letra minúscula ( q) e sua negação por ( ~q)
q: está fazendo sol.
~q = não esta fazendo sol.
Simbora, para análise das assertivas
A) q ^ ~q
q ~q q ^ ~q
V F F
V F F
F V F
F V F
Pelo visto é uma contradição. Vamos seguindo...
B) q = Sabemos que uma proposição é uma declaração, ao qual pode-se atribuir V ou F ( sendo assim é contingência). Seguindo..
C) q ---> ~q
q ~q q ----> ~q
V F F
V F F
F V V
F V V
Também é contingência, vamos seguindo pessoal...
D) ~q = Sabemos que uma proposição é uma declaração, ao qual pode-se atribuir V ou F ( sendo assim é contingência). Seguindo..
E) q v ~q
q ~q q v ~q
V F V
V F V
F V V
F V V
É UMA TAUTOLOGIA!!!!
Questão tranquila.
Edson Marques
OBRIGADO
Resposta letra (E)
P --> ~P = Tautologia
V F = V
F V = V
e) Está fazendo sol ou não está fazendo sol.
pessoal .. como eu sei se julgo possibilidades começando com verdadeiro ou falso? por ex nessa questão
Está fazendo sol ou não está fazendo sol.
V F
F V
eu poderia dizr q ela esta toda correta ou toda falsa => VV ou FF
thiago trigo pq vc ta usando VVFF (na horizontal*) repetindo?
V
V
F
V
LETRA E
Para achar a tautologia utilize a frase clássica de William Shakespeare : Ser ou não ser eis a questão , substituindo :
Está fazendo sol (P) ou (∨) não está fazendo sol (~ P)
CONTINUE ESTUDANDO VAI CHEGAR A SUA VEZ!!
P V ~P (disjunção) - Para o caso, é necessário apenas uma verdade, no caso V ou F = V (tautologia)
Está fazendo sol ou não está fazendo sol (P v ~P)--------------------- (V v F = V)
Não está fazendo sol ou está fazendo sol (~P v P) -------------------- (F v V = V)
Galera o segredo e fazer a simulação das duas maneiras tanto com Verdade quanto com Falso
Letra E . Quando ele diz: Está fazendo sol ou não está fazendo sol, ele está falando a verdade PORQUE não tem como o tempo estar de outra maneira.
Ou está ensolarado ou não está.Espero ter ajudado.
Cuidado marcus, fui massacrada em um grupo de estudos no face ao falar da concorrência.
meu, eu não entendo nada disso nunca. o.O
P v ~Q = F
V v F = V
F v F = F
F v V= V
LOGO É UMA TAUTOLOGIA
PM / SC
AVANTE
SÓ A UMA PREMISSA.
E UMA NEGAÇÃO DELA.
P ~p Pv~P ( NO OU SÓ É FALSO SE TUDO FOR FALSO)
v f V
f v V
SE EU ESTIVER ERRADO ME FALEM, EU ACERTEI ASSIM.
Um enunciado é uma tautologia quando não puder ser falso, um exemplo é:
TAUTOLOGIA = todas as afirmações serem verdadeiras
A- Está fazendo sol e não está fazendo sol.
no conectivo E as proposições não podem ser opostas, por isso essa frase é falsa TIPO: V ^ F = F
B- Está fazendo sol. Aqui só tem uma frase, não da para valorar verdadeiro ou falso
C- Se está fazendo sol, então não está fazendo sol.
NO CONECTIVO SE ENTÃO, UMA FRASE OPOSTA TORNA ELA FALSA SE CONSIDERAR A PRIMEIRA VERDADEIRA E A SEGUNDA FALSA, TIPO: V F= F
D- não está fazendo sol. Aqui só tem uma frase, não da para valorar verdadeiro ou falso
E- Está fazendo sol ou não está fazendo sol.
NO CONECTIVO OU SE AS FRASES FOREM OPOSTA, TORNAM ELAS VERDADEIRAS, TIPO: V v F = V
LETRA E CORRETA
Quando tiver uma afirmação e uma negação da afirmação ligadas pelo conectivo OU sempre será uma tautologia.
Está fazendo sol ou não está fazendo sol.
Afirmação v negação da afirmação = TAUTOLOGIA.
Está fazendo sol ou não está fazendo sol.
Está fazendo sol = p
Não está fazendo sol = ~p
p- --- ~q --p V ~p
V ----- F ------ V
F ----- V -------V (TAUTOLOGIA)
conectivo ou é disjunção inclusiva, pela tabela verdade:
p---- q --p V q
V --- V ----V
V --- F ----V
F --- V ----V
F --- F ---- F
Dentre as alternativas abaixo e considerando o valor lógico das proposições compostas, a única falsa é:
Dicas:
"E" só será V se ambas forem V
"OU" só será F se ambas forem F
"se...então..." só será F se a 1ªV e a 2ªF
"se somente" só será V se ambas forem V ou ambas forem F
b) V e F = Vera Fiche = Falso
Caro Mariston Cleber, isso não é caso de condicional ("verá ficher"). A alternativa b é uma conjunção ("e") que só é v quando os dois são v.
Espero ter ajudado.
Bons estudos.
a) V v F = V
b) V ^ F = F (única falsa)
c) F -> F = V
d) F <-> F = V
Letra b) é a Falsa
Para que a proposição composta formada pelo conectivo "e" introduzindo uma conjunção seja verdadeira, ambas as proposições simples que a compõe devem ser verdadeiras.
(4 + 4 = 8) e (3 + 5=7)
V ^ F = Falso
GABARITO. B.
ESQUEMA
P Q
a) V v F =V
b) V ^ F = F
c) F -> F = V
d) F <-> F = V
GABARITO: B
O E (^) será FALSO quando pelo menos uma proposição for falsa.
ATENÇÃO!!! O "MAS" também representa o conectivo "e",
B) V^F=F
FOCA NELESSSS!!! rsrs
Conjunção: a operação da conjunção liga duas ou mais proposições simples pelo conectivo “e” (^). Observemos o exemplo:
Irei ao cinema e ao clube. Vamos montar a tabela verdade para a proposição composta destacando todas as valorações possíveis.
Conjunção: p^q (p e q)
P Q P ^ Q
V V V
V F F
F V F
F F F
http://www.infoescola.com/matematica/conectivos-logicos/
No exemplo colocado na letra "b" a primeira afirmação é verdadeira, mas a segunda é falsa, por isso, a temos como a opção falsa do exercício.
(4 + 4 = 8) e (3 + 5=7) -> FALSA
Bons estudos e boa sorte!
lembrar que
ou = sempre que for F + F = Falso (o resto é Verdadeiro)
e = sempre que for V + V = Verdadeiro (o resto é Falso)
se..., entao, é condicional = -> sempre que for V + F = Falso (Vai Fugir = Foge), o resto é verdadeiro
se somente se, é bicondicional = <-> sempre que for V+V ou F+F = Verdadeiro (o resto é Falso)
Olá pessoal,
Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/JaRmVQuW6_g
Professor Ivan Chagas
www.gurudamatematica.com.br
B
(4 + 4 = 8) e (3 + 5=7) CONECTIVO E = PARA SER VERDADEIRA TODOS TEM QUE SER VERDADEIROS
PM/SC
AVANTE
GAB= B
TABUADA LÓGICA
"e => tudo V DÁ V
"ou => tudo F DÁ F
"ou... ou => Iguais dá F Diferentes dá V
"se..., então => V COM F DÁ F
"se e somente se => Iguais dá V; Diferentes da F
Questão massa!!!
a) V ou F = V: Na Disjunção só e falso quando todas são falsas.
b) V e F = F: Na Conjunção só é verdade quando todas forem verdade.
c) Se F, Então V = V: Na condicional só é falso quando a 1a Verdadeira e 2a Falsa.
d) F Se, e somente se, F = V: Na Bicondicional só é falso quando os valores forem diferente.
Questão bacana demais! Muito boa
VAMOS ATRIBUIR VALORES AS DEMAIS PROPOSIÇÕES:
A V F
(3 + 4 = 7) ou (25% de 60 = 18)= V
B V F
(4 + 4 = 8) e (3 + 5=7)= F
C F F
Se (2 + 3 = 4), então (1 + 4 = 3)= V
D F F
( 1 + 4 = 4) se, e somente se, (2 + 3 = 6)= V
"E" só será V se ambas forem V
"OU" só será F se ambas forem F
"se...então..." só será F se a 1ªV e a 2ªF
"se somente" só será V se ambas forem V ou ambas forem F
ESPERO TER AJUDADO!
Determine o número de linhas da tabela-verdade da proposição: “Se trabalho e estudo matemática, então canso, mas não desisto ou não estudo matemática”.
Gabarito A!
São 4 enunciados (proposições simples). (trabalho=Q, estudo=R, canso=S e desisto=T)
Nº de linhas= 2 elevado aos enunciados. = 2 elevado a quarta potência = 2x2x2x2=16
LEMBRANDO!!!
Para o cálculo do número de linhas, "negação e afirmação" de uma mesma partícula, conta-se apenas como um átomo. Ou seja, Q e ~Q são equivalentes a, "apenas", uma partículaA proposição acima fica: (p ∧ q) --> r / ~s v q
4 variáveis.
2 sentenças: V e F
o número vai ser sempre elevado a 2
4 elevado a 2 = 16
Se trabalho (1) 4
^
estudo matemática (2) 8
----->
então canso, mas não desisto (3) 12
v
não estudo matemática (4) 16 linhas...
“Se trabalho = p
e estudo matemática = q
então canso = r
mas não desisto = s
ou não estudo matemática = \/ ~q
4 proposições = 2^4 <-> 16
FÓRMULA =2n
P Q
V=V
V=F ======4 LINHAS.
F=V
F=F
EXISTEM 4 CONECTIVOS NA QUESTÃO .
PARA CADA CONECTIVO USAREMOS 4 LINHAS PARA FORMAR A TABELA VERDADE.
1 SE E ENTÃO = 4 LINHAS
2 CONJUNÇÃO = 4 LINHAS
3 DISJUNÇÃO INCLUSIVA= 4 LINHAS
4 NEGAÇÃO =4 LINHAS
4+4+4+4 = 16.
(((TOTAL 16 LINHAS))).
A proposição “Se trabalho e estudo matemática, então canso, mas não desisto ou não estudo matemática” possui 4 proposições simples e distintas.
Daí, o número de linhas da tabela verdade será 2^4 = 16 linhas.
São 4 enunciados (proposições simples). (trabalho=Q, estudo=R, canso=S e desisto=T)
e a que seria a 5º não entra na contagem porque é a negação de uma já existente = (NÃO estudo matemática)
Nº de linhas= 2 elevado aos enunciados. = 2 elevado a quarta potência = 2x2x2x2=16
Se você achar que tem 5 ou 3 proposições, nenhum resultado fecha porque o número de linhas da tabela verdade é o número de proposições elevado a 2
P ^2
4^2 = 16
2^n (==> n = 1)trabalho, 2)matemática, 3)canso, 4)desisto) ==> 2^4 = 16.
São 4 conectivos
portanto deve multiplicar: 2x2x2x2= 16 linhas
Resposta correta:Letra A
Questão excelente para treinar o número de linhas da tabela-verdade.
Para responder a questão, além de calma é preciso analisar a proposição:
“Se trabalho e estudo matemática, então canso, mas não desisto ou não estudo matemática”.
Vamos separar:
A: trabalho
B: estudo matemática
C: canso
D: não desisto
NÃO ESTUDO MATEMÁTICA É UMA NEGAÇÃO DE ALGO EXPOSTO ANTERIORMENTE, NESTE SENTIDO, NÃO HÁ NECESSIDADE DE INCLUIR NA DESCRIÇÃO.
2^4:16
2021: um ano de vitória.
GABARITO: A
“Se trabalho e estudo matemática, então canso, mas não desisto ou não estudo matemática”.
Percebemos que temos 4 proposições
Como saber o número de linhas da tabela-verdade = 2^n
2^4 = 2 . 2 . 2 . 2 = 16 linhas.
Adriano disse: Beto mente.
Beto disse: Cadu mente.
Cadu disse: Adriano e Beto mentem.
Para não haver contradição lógica nas três afirmações, das três pessoas, diz a verdade apenas
GENTE POR FAVOR NÃO CONSEGUI RESOLVER ESSE ALGUEM SABE?..PORQUE SE FOR CONSIDERAR QUE BETO FALA VERDADE ENTAO PELA AFIRMAÇÃO DE CADU SE ADRIANO MENTE ENTAO CADU TA FALANDO A VERDADE NO CASO DO ADRIANO E MENTINDO NO CASO DO BETO
Vou tentar explicar de maneira prática
Como não há contradição, não faremos aquele jogo da contradição (às premissas que se contrapõem dá-se o valor V ou F de maneira que uma recebas o V e a outra receba o F). VAMOS AO QUE interessa.
Silvana, deve-se fazer teste com cada uma das AFIRMAÇÕES:
Se dermos o valor V para o ADRIANO, perceba que haverá invalidade de ideias, visto que, se BETO MENTE e o proprio diz que CADU MENTE (perceba que o BETO MENTE), então o CADU FALARÁ A VERDADE, ocorre um CHOQUE pq o CADU fala a verdade, mas diz que o ADRIANO mente (na situação é considerado V).
Para não me estender no assunto, BASTA QUE VOCÊ ATRIBUA UM "VERDADEIRO" a cada um por vez para testar.
LETRA B
Considerando que Beto fala a verdade, então Cadu Mente. Se Cadu Mente, não é verdade que Adriano e Beto mentem, pois Beto fala a verdade. Assim como não é verdade quando Adriano diz que Beto mente, pois Beto fala a verdade.
Se Beto diz a verdade -> C mente
C diz que A e B mentem -> portanto A e B falam a verdade
A diz que = B mente logo já temos uma contradição lógica aí.
Não tem como ser esse o gabarito.
Resolvi dessa forma:
1 - Adriano disse que Beto mente. (ok, vamos considerar verdadeira);
2 - Beto disse: Cadu mente (considerando o que já sabemos da frase anterior - que Beto mente - então Beto está mentindo e Cadu NÃO mente);
3 - Cadu disse: Adriano e Beto mentem (ok, já sabemos que Beto mente! Mas e Adriano?! Ora, se Adriano mente então a frase 1 é Falsa - é como descobrir um novo segredo e voltar a solucionar o caso);
Volta pra frase 1 então pra "corrigir"...
1 - Se Adriano mente, logo, Beto NÃO mente nada!;
2 - Então a frase 2 é correta e diz que Cadu mente;
3 - Se Cadu mente e disse que Adriano e Beto mentem, isso é falso. Beto não mente e Adriano pode até mentir (como já descobrimos antes que mente), mas mesmo assim a frase de Cadu continuará sendo mentirosa, pois inclui Beto.
Eu não sei qual é a forma matemática de resolver isso, mas gostaria de saber.
considerando V Adriano: Beto mente (ok, beto vai falar uma mentira)
F Beto: Cadu mente( ok, já sei que ele ta mentindo, então Cadu fala a verdade)
F Cadu: Adriano e Beto mentem (Ora! para um "e" ser falso, uma das duas premissas tem que ser falsa e a outra verdadeira, assim como para ser verdade, as duas terão que ser verdadeiras. Se Beto ai diz que Cadu mente, e isso é verdade, enão ele nao ta falando nenhuma mentira e sim uma verdade, como pode falar uma verdade se atribuimos um F a ele?
Considerando F Adriano: Beto mente ( isso é mentira, já que é falso então beto fala a verdade)
V Beto: Cadu mente ( o que ele diz é verdadeiro que cadu mente.)
F Cadu: Adriano e Beto mentem( para que essa proposição seja falsa basta que uma delas seja falsa. Adriano mente? (V) isso é verdade "E" Beto mente? (F) beto fala a verdade = então V e F = F... A proposição de fato é F como consideramos. Beto fala a verdade Letra B.
So pra testar a ultima proposição como V:
Considerando F Adriano: Beto mente (ok, isso é mentira, já que é falso então beto fala a verdade)
F Beto: Cadu mente ( ok, já sei que ele ta mentindo, então Cadu fala a verdade)
V Cadu: Adriano e Beto mentem( Se isso é verdade, choca com o que dissemos acima que Adriano mente e Beto mente) Então só pra testar mesmo. Mas já haviamos descoberto que o V em Beto foi o que deu mais certo na alternativa
Se Beto diz que Cadu mente, e Cadu diz que Beto mente, eles estão se contradizendo, então um deles diz a verdade e o outro mente.Se sabemos que um deles diz a verdade e apenas um diz a verdade, podemos descartar Adriano e afirmar que ele mente...se Adriano mente, quando afirma que Beto é mentiroso, podemos concluir que Beto é quem diz a Verdade.
O comentário de Renato Bocx foi objetivo e direto. Deu para entender!!
Suposição 1: Cadu diz a verdade e Adriano e Beto mentem.
Cadu: Adriano e Beto são mentirosos (V)
Adriano: Beto é mentiroso (F) --> ou seja, Beto diz a verdade. Já deu erro! Só um pode dizer a verdade, Beto deveria ser mentiroso.
Beto: Cadu é mentiroso
Cadu não pode ter dito a verdade. Suposição 2: Cadu mentiu.
Cadu: Adriano e Beto são mentirosos (F) --> Isso significa que um deles diz a verdade, já que o problema não permite que os dois digam.
Adriano: Beto é mentiroso (em vez de chutar, é melhor olhar para a afirmação de Beto e ver se faz sentido).
Beto: Cadu é mentiroso (V) Opa... Cadu é mentiroso mesmo, de acordo com esta segunda hipótese. Beto diz a verdade.
gabarito: letra B
Resolução de contradições:
1) Assumir que uma pessoa está falando a Verdade Universal (VU).
2) a partir dessa Verdade Universal, continuar a linha de pensamento até voltar para a pessoa que falou a VU. Se tivermos VU + V, está OK.
Primeiro caso: Adriano fala a VU
A-B = VU
B-C = ?
C-AB = ?
essa VU diz que: B está mentindo.
Se B está mentindo quando diz que "C mente", então C está falando a verdade:
A-B = VU
B-C = M
C-AB = V
agora precisamos voltar para a nossa VU a partir da última premissa C.
C disse que A e B mentem:
A-B = VU + M
B-C = M + M
C-AB = V
opa, deu VU+M. Isso ta em contradição. Errado. Vamos tentar a VU para a segunda pessoa:
A-B = ?
B-C = VU
C-AB = ?
B fala que C mente:
A-B = ?
B-C = VU
C-AB = M
C fala que A e B mentem, mas ja sabemos que isso eh falso. Então A e B falam a verdade:
A-B = V
B-C = VU + V
C-AB = M
Certo! VU + V fica OK. Então só a segunda pessoa (Beto) fala a verdade.
Gabarito: B
Para Cadu mentir, há três possibilidades:
V e F
F e V
F e F
Adriano: (Beto mente) F
Beto: (Cadu mente) V
Cadu: (Adriano mente)V e (Beto Mente) F
Não consegui entender como chegar a resolução dessa questão, uma vez que, Se a frase mentirosa de Adriano, faz a do Beto ser verdade, como a mentira de Cadu pode ser ignorada? pq ele diz que Adriano e Beto mentem, isso sendo mentira, não tornaria a fala de Adriano verdadeira também?
Se 1 fala a verdade, então 2 mentem. É só focar na contradição da verdade. (1V,2M)
Opção 1
(VERDADE) Adriano : Beto mente. "VALE"
(MENTE) Beto : Cadu não mente. "parou, Contradiz Cadu ,pois ele mente"
(MENTE) Cadu : Adriano Beto mentem.
Opção 2
(MENTE) Adriano : Beto não mente. "vale" -> realmente beto fala a verdade.
(VERDADE) Beto : Cadu mente. "vale" -> sim, cadu é mentiroso.
(MENTE) Cadu : Adriano ou Beto não mentem. "vale" -> sim, Beto não mente.
Opção 3
(MENTE) Adriano : Beto não mente. "parou, Contradiz Beto pois ele mente"
(MENTE) Beto : Cadu mente.
(VERDADE) Cadu : Adriano e Beto mentem.
Conclui-se que Beto que fala a verdade.
Essa é só pros fortes HAHAHA
Dica: Em RLM temos que esquecer o senso comum, logo negação de E é OU.
EXPLICAÇÃO MUITO SUPERFICIAL DESSE PROFESSOR
C - A mente, pois eu minto e B mente também pois eu falo a verdade! (o que???)
A - C fala a verdade, B mente (afirmando que o fumado do C fala a verdade??)
B - C mente ( A vá!!)
ADRIANO DISSE: Beto mente V F F
BETO DISSE: Cadu Mente F V F
CADU DISSE: Adriano e Beto Mentem F F V
*Façam todas as possibilidades.
Na primeira possibilidade-> Se Adriano diz a verdade, logo BETO e CADU estão mentindo= Adriano também mente (errada)
Na segunda possibilidade-> Se Beto diz a verdade, logo CADU mente, então Adriano está mentindo e BETO diz a verdade (correta)
Na terceira possibilidade-> Se Cadu diz a verdade, logo ADRIANO e BETO mentem, e ADRIANO diz apenas que Beto mente, então pela fala de Cadu, entende-se que ele mesmo está mentindo e BETO diz a verdade.
Se Adriano mente, então Cadu não mente quando diz que Adriano mente. Não? Help!
Para resolvermos este tipo de questão, devemos fazer três testes, os quais podemos considerar como VERDADEIRO um de cada vez.
Primeiro vou dizer que Adriano disse a verdade e testar com as demais afirmações. Depois com Beto e por último Cadu.
Obs. Posso começar por qualquer um dos 3. Se der sorte já mata a questão de cara...
Vamos lá...
Vamos dizer que BETO disse a verdade, ok?
Se Beto disse a verdade, então Adriano mente. Pois Adriano diz que Beto mente, e como já sabemos, Beto diz a verdade.
Beto diz a VERDADE e Adriano MENTE, beleza, mas...e o CADU?
Cadu diz que Beto e Adriano mentem...OPA!!!!! já está mentindo, pois BETO diz a VERDADE e somente o ADRIANO MENTE.
Adriano mente
Beto diz a verdade
Cadu mente
Essa daí puxei no fundo do baú do psicológico kkkk...duas horas pra acertar! Só lembro que quando vi uma vez o professor fazendo uma parecida, ele ia testando até ver se a conclusão batia! Não sei explicar como faz essa não kkkkk
Cara, fui assistir a aula do professor complicou mais ainda meu raciocínio. kkk esse professor é péssimo!
Os irmãos Alan, Bruno, Caio e Danilo, estavam sentados à mesa para tomar o café da manhã, e eis que um deles derrubou leite na toalha. A mãe deles procurou saber quem derramou o leite na toalha, ao que Alan logo se prontificou a responder que não o fez. Bruno disse que foi Caio e Danilo disse que foi Bruno. Caio, por sua vez, disse que Danilo está mentindo. Sabendo que apenas um dos irmãos não diz a verdade, é correto afirmar que quem derrubou o leite na toalha da mesa foi:
alguém sabe o porquê?
Alan= não fui EU
Bruno= foi caio
Caio= danilo mentiu
Danilo= foi bruno.
Devemos achar a contradição, que esta entre caio e danilo. Como só um esta mentindo então só pode ser danilo o mentiroso, logo caio derrubou o leite.
Tentarei explicar:
Nesse tipo de questão devemos resolver pelo método da tentativa, ou seja, consiste em deduzir que um deles está mentindo e os outros três falam a verdade, para isso faremos uma tabelinha e chamarei H1(hipótese 1) H2(hipótese 2) H3(hipótese 3) H4(hipótese 4).
H1 H2 H3 H4
ALAN F V V V
BRUNO V F V V
DANILO V V F V
CAIO V V V F
hipótese 1 = nessa hipótese vamos considerar que Alan está mentindo e os demais dizendo a verdade, nessa situação quando Alan diz "não fui eu" é mentira portanto concluímos que foi ele, mas percebemos em seguida que Bruno ao dizer "foi Caio" pela tabela que fizemos está dizendo a verdade então Caio também derramou o leite e como SOMENTE um o fez essa hipótese gera inconsistência.
hipótese 2 = nessa hipótese quem agora está mentindo é Bruno. Quando Alan diz "não fui eu" ela está falando a verdade portanto concluímos que não foi ele, em seguida Bruno diz "foi Caio" sendo essa afirmação falsa deduz que NÃO foi Caio, logo Danilo disse "foi Bruno" e como ele fala a verdade conclui-se que foi o Bruno, mas Caio diz que o Danilo está mentindo e como na tabela os dois dizem a verdade não sabemos em quem confiar portanto gera inconsistência.
hipótese 3 = nessa hipótese quem está mentindo é o Danilo, vamos lá: Alan diz "não fui eu" como ele fala a verdade então NÃO foi ele. Bruno diz "foi Caio" como ele fala a verdade então concluímos que foi Caio. Danilo diz "foi Bruno" como ele está mentindo NÃO foi o Bruno e por último Caio diz "Danilo está mentindo" e de fato Danilo menti de acordo com a tabela, ou seja Caio derrubou o leite e Danilo é o mentiroso. Gera consistência!
hipótese 4 = nessa hipótese quem está mentindo é o Caio. Quando Alan diz "não fui eu" ele fala a verdade então não foi ele. Bruno diz "foi caio" como ele fala a verdade então foi Caio. Danilo diz "foi Bruno" e como também fala a verdade deduzimos que Bruno também derrubou o leite, portanto gera inconsistência tendo em vista que somente um derramou.
Deus é pai!!!!
GAB: C!
X: Alan, disse que não foi ele e ninguém discordou.
Z: Caio foi acusado por Bruno e não discordou.
T: Danilo acusou Bruno, mas Caio o defendeu dizendo que Danilo está mentindo.
Caio pronunciou-se para defender outro irmão ,e não se defendeu quando foi acusado. Logo o mais suspeito é o Caio.
a questão diz: SOMENTE UM NÃO DIZ A VERDADE OU SEJA 1 ESTÁ MENTINDO
ALAN -> diz que não foi ele (v)
Bruno -> disse que foi CAIO (V)
Caio -> disse que DANILO está mentindo (v)
Danilio -> disse que foi bruno (F) pq foi CAIO
Se mudar os valores de qualquer um não fecha
Conforme a teoria da lógica proposicional, a proposição ~ P Λ P é:
~p ^ q é sempre uma contradição
Lembre-se da propriedade comutativa da conjunção
~p ^ q = q ^ ~p
Letra c)
Acrescentando
p v ~p É sempre tautologia , também admite-se a comutatividade
Eu acho mais fácil assim:
Afirmou, colocou "ou" (V) e negou = tautologia
Afirmou, colocou "e" (^) e negou = contradição
Bons estudos
Tautologia é uma proposição composta que SEMPRE é verdadeira (na tabela-verdade), independentemente dos valores das proposições.
Se P fosse V a negação de P seria F.
Se P fosse F a negação de P seria V.
Como é ~P ^ P não pode ser tautologia, porque na conjunção para dar V as duas proposições devem ser V
Contradição - mesma lógica, só que ela é SEMPRE falsa.
P ~P ~P^ P
V F F
F V F
então é contradição. (letra C)
ps. contingência é quando apresenta pelo menos uma vez os valores V e F.
Neyma é Falso => nega o primeiro e mantém o segundo, contradição!
Maus aí Neymar ;D
Como podemos verificar na tabela abaixo:
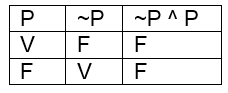
Temos uma contradição, pois é uma proposição cujo valor lógico é sempre falso.
Resposta : C
Lembrando os conceitos:
Tautologia: ocorre quando proposições compostas apresentam
tabela-verdade sempre com valores lógicos verdadeiros, independentemente
dos valores lógicos das proposições simples que as compõem.
Contradição: ocorre quando proposições compostas apresentam
tabela-verdade sempre com valores lógicos falsos, independentemente dos
valores lógicos das proposições simples que a compõem.
Contingência: ocorre quando não houver tautologia e nem
contradição, ou seja, quando na tabela-verdade houver ocorrências verdadeiras
e falsas.
BIZU do professor Renato Oliveira aqui do Qconcurso:
1) Quando a primeira proposição for uma AFIRMAÇÃO e a segunda proposição for uma NEGAÇÃO (vice-versa) e elas forem ligadas pelo operador E
logo tem-se uma CONTRADIÇÃO.
2) Quando a primeira proposição for uma AFIRMAÇÃO e a segunda proposição for uma NEGAÇÃO (vice-versa) e elas forem ligadas pelo operador OU logo tem-se uma TAUTOLOGIA.
A OU não A - Tautologia
A E não A - Contradição
Afirmo OU nego -----> tautologia lembre que OU é "tOUtologia"
Afirmo E nego ---> está se contradizendo é uma contradição
Comentário dessa questão no Youtube.
Questões Comentadas Professor Ivan Chagas (do Canal Guru da Matemática)
0869 - ESAF - INTRODUÇÃO A LÓGICA PROPOSICIONAL
https://www.youtube.com/watch?v=r8CsKhtku4Y
Veja que a conjunção “~P e P” é uma contradição, pois esta proposição é falsa tanto quando P é V como quando P é F.
Resposta: C
Assinale qual das proposições das opções a seguir é uma tautologia.
Questão simples.
Tautologia --> Quando uma proposição qualquer, for sempre "V"erdade, independentemente dos valores lógico das proposições que a compõe.
p ^ q --> q
p q p^q p^ q ---> q
V V V V
V F F V
F V F V
F F F V
Letra b)
TAUTOLOGIA = Toda "V";
CONTRADIÇÃO = Toda "F";
CONTINGÊNCIA = Não é toda "V", nem toda "F".
A letra a é contingência e a letra b é tautologia.
RESPOSTA LETRA B
Não entendi... Para mim, as alternativas "b" e "c" são verdadeiras. Na letra "c", a bicondicional não fica com as duas partes iguais? Não entendi foi nada...rs
Resolução completa da questão no link abaixo:
https://www.youtube.com/watch?v=Qk3g67AsxkE
Comentário dessa questão no Youtube.
Questões Comentadas Professor Ivan Chagas (do Canal Guru da Matemática)
0867 - ESAF - TAUTOLOGIA
https://www.youtube.com/watch?v=zpQCBuTYvoA
p q p^q (p^q)->q
V F F V
F V F V
LETRA B
Para ser uma tautologia, não pode haver uma situação onde a proposição resulta em valores lógicos falsos. Vejamos:
a) 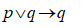
Não é tautologia, pois quando p é V e q é F temos V→F, que é FALSO.
b) 
É uma tautologia. Construa a tabela-verdade desta proposição para confirmar. Você verá algo assim:
c) 
Não é tautologia, pois quando p é F e q é V temos F<==>V, que é FALSO.
d) 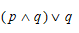
Não é tautologia, pois quando p e q são ambas F, ficamos com FvF, que é FALSO.
e) 
Não é tautologia, pois quando p é V q é F temos V⇔F, que é FALSO.
Resposta: B
Gabarito: B
Principais Regras:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
O segredo dessa questão estava na precedência dos conectivos lógicos:
1º - realizar as operações de negação;
2º - realizar as operações de conjunção;
3º - realizar as operações de disjunção;
4º - realizar as operações de condicional.
Sucesso e grande abraço!
Dadas quaisquer proposições p e q, a proposição composta (p ∧ q) ∨ (∼p ∧ ∼q) é uma tautologia.
(p ∧ q) ? (~p ∧ ~q)
(p ∧ q) -> (~p ∧ ~q) *** Não é tautologia***
Fazendo a tabela verdade, o resultado é: V F F V ou seja, não é tautologia.
Prezados colegas, resolvi da seguinte maneira, porém gostaria do comentário de vocês para saber se realizei a questão de maneira correta:
Parti do princípio básico de matemática, primeiro resolvo o que está entre parênteses e depois os demais.
Sendo assim, o resultado da primeira preposição será:
primeira preposição
p e q - na conjunção as duas afirmativas têm que ser verdadeiras para ser válida. logo, é Verdade
segunda preposição
não p e não q - na conjunção as duas afirmativas têm que ser verdadeiras para ser válida a sentença, logo é Falsa
Agora temos: V DISJUNÇÃO F
Nesse caso, a disjunção só não será válida se o resultado for (FAFÁ DE BELÉM) F e F. Como encontramos V e F, a disjunção será verdadeira.
Sendo assim, é uma tautologia.
Questão tranquila.
''ERRADO''
É uma CONTINGÊNCIA.
Contingência ;)
SÉRIA, SO A INVERSÃO " ^ " PARA " V " SIMPLES.
Galera, macete para saber quando temos tautologia sem precisar de tabela verdade:
PROPOSIÇÃO v NEGAÇÃO DA PROPOSIÇÃO (disjunção)
PROPOSIÇÃO v NEGAÇÃO DA PROPOSIÇÃO (disjunção exclusiva)
PROPOSIÇÃO -> EQUIVALÊNCIA DA PROPOSIÇÃO (condicional)
PROPOSIÇÃO < - > EQUIVALÊNCIA DA PROPOSIÇÃO (bicondicional)
Nesses casos SEMPRE teremos tautologia.
Alguém pode me ajudar? Eu entendi o resultado da tabela VFFV, mas olhando essa proposição vi, pelo jeito, equivocadamente, que se tratava de um caso trivial de tautologia, por ex, quando temos "P v ~P" ou ainda "(P ^ Q) v ~(P ^ Q)". Neste último caso, não seria O caso da questão? Agora não entendi nada.
Pessoal, quem tiver dúvida sobre a maneira de resolver essa questão, pode me pedir por e-mail.
NÃO CONSIGO COLOCAR A TABELA AQUI. :(
Email: renata20_mello@hotmail.com
P.S. A tabela que faço é simples e fácil de entender.
Na minha resolução deu
P ^ Q = (~p ∧ ~q) =
V V V F F F
F F F V V V
V F V F V V
F V V V F V
resultado:
(P ^ Q) v (~P ^ ~Q) =======
v f f
f v f
v v v
v v v
É UMA CONTINGÊNCIA!
RESULTADO DA TABELA
V
F
F
V
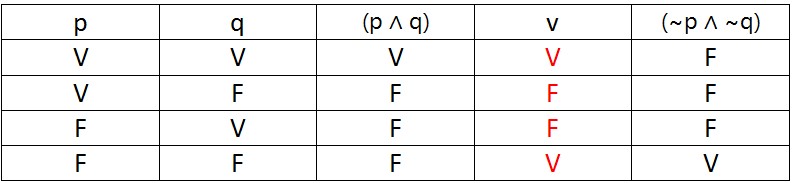
galera , vejo muitos comentários ae, e não sei se estão certo.. resolvi assim como o Eduardo Orem.. é uma tautologia, pois a disjunção não tem como ser falsa.
Uma dica: Parem de ficar procurando BIZU sobre RLM, pois isso só vai complicar vocês cada vez mais. RLM é uma matéria tranquila quando se aprende de maneira simples e correta.
Indico o Prof.Josimar Padilha, é excelente !!
Força guerreiros!!
Primeiro você deve negar se de certo nao é tautologia, se não der, então é
P Q ¬P ¬Q P^Q ¬P^¬Q (P^Q) V(¬P^¬Q)
V_____V _____F_____F______V________F____________V
V_____F______F_____V______F________F____________F
F_____V______V_____F______F________F____________F
F_____F______V_____V______F________V____________V
O NEGOCIO CHATO PARA FAZER TABELA AQUI É UMA BICODICIONAL RSRS ou uma contigência ^^
é uma contigência.
Gente quando penso que guardei a tabela verdade eu vejo questoes assim e me ferro, eu aprendir que na tabela da conjunção (^) só é verdade quando tudo for verdade eu estou vendo comentários aqui colocando verdade quando um dos conectivos for falso ou verdadeiro, isso procede? errei a questao porque fiz como aprendi de acordo com a tabela verdade da conjunçao, Por favor algum professor grave explicaçao
P Q P ^ Q v ~P ^ ~Q
V V V V F F
V F F V F V
F V F V V F
F F F V V V
Agora minha dúvida na tabela da disjunção inclusiva (v) "OU" somente será falsa quando da tudo falso, se eu estou comparando a tabela do P^Q usando conectivo OU
entre ~P ^ ~ Q EU TENHO QUE CONSIDERAR A TABELA do (v) "OU" , então alguém me explica porque não deu o resultado acima? NESTE RESULTADO é Considerado uma tautologia
Resultado: VFFV
É só olhar e vê se são equivalentes,caso não sejam nunca será tautologia.
Pau no Burro.
Sendo p, q e r proposições quaisquer, na tabela-verdade da proposição composta (p ∧q)∨ (~p ∧ r) ∨ (~q ∧ ~r) existem exatamente três linhas nas quais p é falsa, e essa proposição composta é verdadeira.
Certo.
Vou tentar uma tabela verdade, a resposta está em negrito.
p q r ~p ~q ~r (p ^ q) (~p ^ r) (~q ^ ~r) [(p^q) v (~p^r) v (~q^~r)]
__________________________________________________________
v v v f f f v f f v
v v f f f v v f f v
v f v f v f f f f f
v f f f v v f f v v
f v v v f f f v f v
f v f v f v f f f f
f f v v v f f v f v
f f f v v v f f v v
Minha Tabela ficou certinha! Só não tô conseguindo interpretar a resposta!
Acredito que minha tabela esteja certa, com somente duas linhas falsa.
Cara, minha tabela só dá 2 linhas falsas... Alguém socorre?
Fiquem com DEUS!
A questão pede as linha em que P é falsa mas a proposição final seja verdadeira.Temos quatro possibilidades para P falso, mas apenas em três delas a proposição final é verdadeira, como na tabela do Gleber.....
Minha tabela ficou igual a do colega abaixo, mas marquei errado. Não entendi nadica de nada do que a questão queria na verdade rsrsrsrsrsrs.....
Vou tentar colocar uma tabela aqui
P Q R P ^ Q ~P^R ~P^~R (P^Q) V (~P^R) V (~P^~R)
v v v v f f v
v v f v f f v
v f v f f f f
v f f f f f f
f v v f v f v
f v f f f v v
f f v f v f v
f f f f f v v
Eu não sei se eu entendi errado essa questão, mais me parece que ela quer saber se existem exatamente três linhas nas quais P é falsa, e essa proposição composta é verdadeira.
Confesso que não estou conseguindo ver essa questão como CERTA.
Alguém poder ajudar?
Eu também não consegui interpretar esta questão. Minha tabela verdade ficou igual a do Clayton. Não entendi como a resposta pode estar certa, se só há duas linhas em que o resultado dá "F" e no final para que a questão composta seja verdadeira, eu entendo que todas as linhas deverão ser "V".
Questão mal formula, três linha, onde? na vertical, horizontal, diagonal. O primeiro comentário que achou as três linhas não esta somente em P, portanto incorreto.
"três linhas nas quais p é falsa E essa proposição composta é verdadeira".( isso já é uma proposição!!! em que as duas tem que ser verdade, pois tem conectivo E)
Sim existe quatro F em P, porém somente 3 que tenha como a proposição composta como verdadeira.
Ao desenrolar da tabela vai ficar assim:
p (p^q) v (~p^r) v (~q^~r)
v v
v v
v f
v v
f v
f f (essa linha não conta pois os dois são falsos)
f v
f v
então existe exatamente três linhas nas quais p é falsa E essa proposição composta é verdadeira. =D
Resposta C
CESPE , ou vc entende a questao ou vc erra.
poxa, fiz a tabela no meu caderno e deu 4 de v e 4 alternativas com f, professores, ninguém está achando a resposta correta desta questão, ajudem-nos
gente no final o meu deu assim:
v
v
f
v
f
v
f
v 3 f , seria a resposta?
fiz a tabela, deu tudo certo mais não soube interpretar a questão :(
Não entendi nada...
Ajudaaa
Questão muito confusa. Fazer a tabela verdade é fácil. O difícil é interpretar a questão.
Também tive dúvidas na interpretação da questão. Mas acredito que está correta a explicação do Pedro Reis.
Demorei para interpretar. Acho que fica mais fácil assim: Existem 3 linhas nas quais P é falso e a prop composta. é V (ao mesmo tempo). É só visualizar a tabela, não precisa resolver mais nada. Não deveria ter a vírgula depois de "falsa".
Oli Luiz Fernando!
Onde sua tabela está dando duas falsas ? Pois se for no inicio já da tabela P na qual é proposição, está incorreto. Lembre-se não são 4 linhas, mas sim 8, então necessariamente tem que ter 4 F e 4 V nas proposição P,Q e R. É só elevar 2 ao cubo ( três proposições). Se fosse somente P e Q, seria 2 ao quadrado , SENDO 4 linhas.
Qualquer dúvida, me mande mensagem!
Cai também...
Infelizmente, é mais falta de atenção e paciência do que erro de anunciado.
Ele diz "p é falsa". Ele diz "p" e não q, nem r, nem (p ∧ q) ∨ (~p ∧ r) ∨ (~q ∧ ~r).
Aí, depois, finaliza... "e essa PROPOSIÇÃO COMPOSTA é verdadeira". Agora sim ele está falando do resultado da tabela-verdade. Sniff! Sniff!
Seria uma questão bacana se esse enunciado não fosse tão confuso, depois de ler várias vezes a questão e o comentário do Pedro Reis consegui compreender que "parece" que a questão quer que haja 3 linhas em que a proposição P apresente valores F e simultaneamente a linha que mostra o resultado da tabela verdade da proposição composta tenha 3 V, ou seja, comparando a proposição P com o resultado da tabela, encontraremos 3 linhas em que a ordem do valores serão F e V. Afff, dificil até de explicar.
A explicação do Marcelo Mendes é a correta!!
A questão diz que existem exatamente 3 linhas em que "P" é F, "e" apenas nessas mesmas 3 linhas, a última coluna da tabela, que expressa a proposição composta, será V.
É uma questão de interpretação do enunciado.
A questão não é difícil e e´muito boa, pois faz pensar e nivela por cima.
Força guerreiros!!
Gabarito: CERTO
É uma questão de interpretação do enunciado.
Devem construir a Tabela-Verdade e analisar se a afirmativa está correta.
Existem exatamente três linhas nas quais " P " é FALSA, e essa proposição composta é verdadeira (na última coluna da tabela, que expressa a proposição composta é VERDADEIRA). Repare aqui...
P Q R P ^ Q ~P^R ~P^~R (P^Q) V (~P^R) V (~P^~R)
v v v v f f v
v v f v f f v
v f v f f f f
v f f f f v v
F v v f v f V
f v f f f f f
F f v f v f V
F f f f f v V
Forte abraço. Bons Estudos! :)
o QUE tá confundindo é neguinho colocando negrito onde não precisa
O negrito tem que estar na coluna P (enunciado pede) e na coluna final da proposição composta (enunciado pede)
P [(p^q) v (~p^r) v (~q^~r)]
V V
V V
V F
V V
F V
F F
F V
F V
Lembrando o que diz o enunciado:
"existem exatamente três linhas nas quais p é falsa, e essa proposição composta é verdadeira."
Questão com o Português errado. Vejamos se estivesse redigido ASSIM:
Sendo p, q e r proposições quaisquer, na tabela-verdade da proposição composta (p ∧q)∨ (~p ∧ r) ∨ (~q ∧ ~r) existem exatamente três linhas nas quais p é falsa, e essaS proposiçÕES compostaS SÃO verdadeiras.
Julgue os próximos itens, considerando os conectivos lógicos usuais ¬, ∧, ∨, →, ↔ e que P, Q e R representam proposições lógicas simples.
trata-se de uma tautologia, pois, independente dos valores atribuídos a P ou Q, teremos sempre uma tabela com os valores verdadeiros.
Pessoal! tem que ficar atento na hierarquia de resolução
1 - ()
2 - []
3 - {}
Símbolos da negação (símbolo ~ e ¬)
Podemos fazer atribuindo qualquer valor para P e Q e a resposta sempre será Verdadeira, ou seja, uma tautologia.1º Vou escolher P-Verdade e Q-Verdade
[(¬P)∨Q]↔{¬[P∧(¬Q)]}
[(F)vV] ↔ {¬[V∧(F)]}
[V] ↔ {¬[F]}
V↔V
V
Para mostrar que será sempre Verdadeira
Agora vou atribuir para P- F e Q-F
[(¬P)∨Q]↔{¬[P∧(¬Q)]}
[(V)vF]↔{¬[F∧(V)]}
[V]↔{¬[F]}
V↔V
V
* Qualquer equivoco me mande uma mensagem.
Essas questoes tao despencando !
So coloca Falso para todos e se no final der VERDADEIRO é TAUTO.
OBS, so serve para proposição que tem mais de um conectivo
certo
[(¬P)∨Q]↔{¬[P∧(¬Q)]}
Resolve a negação da segunda parte: Nega o P, o conectivo e o Q, ficando assim [(¬P)∨Q]↔[(¬P)∨Q].
Verificamos que as proposições são iguais. Logo, se ambas forem F ou V serão tautologias, porque para que um bicondicional seja verdadeiro, é necessário que ambas possuem o mesmo valor lógico.
A questão é : A proposição [(¬P)∨Q]↔{¬[P∧(¬Q)]} é uma tautologia ?
Primeiro:
1- ~P v Q é equivalente a P → Q
2 - P ^ ~Q é equivalente a ~( P → Q)
Segundo:
1 [(¬P)∨Q]↔{¬[P∧(¬Q)]}
2 (~P v Q) ↔ ~ ( P ^ ~Q) - é a mesma coisa do enunciado, só simplificado para facilitar o entendimento.
3 (P → Q) ↔ ~( ~( P → Q) ) - Substituímos pelas equivalências e deixamos o que não poderia ser substituído, no caso a negação.
4 (P → Q) ↔ ( P → Q) - Lembrando que duas negações equivalem a uma afirmação - ~ + ~ = afirmação
5 - O "P → Q" dos dois lados são IGUAIS , nesse caso se um for verdadeiro o outro também será verdadeiro ou se um lado for falso o outro só pode ser falso também.
F ↔ F = V Tabela verdade da bicondicional
V ↔ V = V
É uma tautologia, pois independente dos valores será sempre verdadeiro
RESPOSTA: CERTO
coloque tudo F sim, não faça tabela.. dá tudo certo, pode confiar
Pessoal,
Tenho bastante dificuldade em raciocínio lógico, e eu realmente não consegui entender a questão, vocês ate explicam direito mas quando colocam os símbolos fica esse quadrado no meio, teria como vcs repetirem a explicação? Obrigada!
Entendi dessa forma: não precisa mexer na 2ª preposição, você só tem que se preocupar com a 1ª. Como sabemos para negar uma disjunção é preciso negar tudo e trocar o conectivo V por ^, então teremos [P^(¬Q)]. Ou seja, é igual a 2ª parte , logo é uma tautologia.
Dica do Professor Josimar Padilha:
Quando a questão pede tautologia a partir de uma bicondicional <->, tente igualar essas proposiçõs. Se conseguir, será tautologia, pois na bicondicional, valores iguais(sentenças iguais) é V, ou seja, TAUTOLOGIA.
Essa de valorar tudo com F não funciona. Pois para ser uma tautologia a sentença tem que ser verdadeira atribuindo os dois valores lógicos.
[(¬P)∨Q]↔{¬[P∧(¬Q)]}
P = F
Q = F
R = F
_______________
[ (¬P) ∨ Q ] ↔ { ¬[ P ∧ ( ¬Q ) ]}
[ (V) ∨ F ] ↔ { ¬[ F ∧ ( V ) ]}
[ V ↔ ¬ F ]
[ V ↔ V ] ---------------------TAUTOLOGIA
Segue a explicação!!
https://www.youtube.com/watch?v=xOXoc0Hd_4w
Se colocar todos falsos ou todos verdade, serão ambas tautologia
Gab CERTO.
TAUTOLOGIA = TODOS OS VALORES DA TABELA SÃO VERDADEIROS.
Nessa questão temos uma BICONDICIONAL, ou seja, se ambos os lados forem iguais, é VERDADEIRO.
Agora vamos para a questão:
Perceba que na segunda parte {¬[P∧(¬Q)]} toda a proposição está sendo negada, então vamos negá-la ...
Qual a negação do "e"? É o "ou" negando as duas proposições, então vamos fazer isso ...
¬P v Q (Neguei o P ficou ¬P, mudei o conectivo para o "ou", e neguei o ¬Q ficou Q.
Ficou IGUAL a primeira proposição, ou seja, são iguais, então, SEMPRE VERDADEIRO.
Espero que tenha ajudado alguém, qualquer erro me avisem.
Tautologia Clássica
{(~PvQ)} <-> { ~(P ^ ~Q)}
~P v Q <-> ~ P v Q
P Q__~P Q____~PvQ
V V___F V______V
V F___F F______F
F V___V V______V
F F___V F__ ___V
P Q __~P Q_____~PvQ_______________________~PvQ <-> ~PvQ
V V ___F V________V _____ ___________________V_________ V _____ V
V F___ F F ________F______ ___________________F_________ F______ V
F V___V V________V____________________________ V_________ V______V
F F___V F________V____________________________ V__________V______V
PARA SER UMA BICONDICIONAL AS PREPOSIÇÕES SIMPLES DEVEM TER VALORES LÓGICOS IGUAIS
LOGO É UMA TAUTOLOGIA
só é porq tem aquela negção discreta kk
Gente, alguém me ajuda, fiz a tabela verdade e nao conseguir achar..
Minha contribuição.
PQ [(¬P)∨Q]↔{¬[P∧(¬Q)]}
VV...........V.....<->......V = V
VF...........F......<->......F = V
FV...........V.....<->......V = V
FF...........V.....<->......V = V
Abraço!!!
Somente usar a lei de de Morgan, nega tudo e compara!!!
@glaucia, um erro bem comum é esquecer de negar no final conforme a questão está pedindo, ou resolver na ordem errada dos conectivos. Veja se não foi isso.
Não sei vocês, mas não confio resolver essas questões sem ser na tabela verdade. Perco um tempo a mais, mas compenso em Direito. 2 proposições é fácil fazer a tabela e vai te fazer ter certeza.
Se durante a prova tiver sem tempo e não quiser deixar em branco, marca como verdadeiro esse tipo de questão. 90% das questões do cespe que cobra tautologia e o conectivo é SE SOMENTE SE a resposta é verdadeira.
Note-se, porém, que o '¬' está fora dos '[ ]', ou seja, tudo que está dentro dos colchetes deve ser NEGADO.
Veja-se:
[(¬P)∨Q]↔{¬[P∧(¬Q)]}
Fica assim:
ñP ou Q ↔ ñP ou Q
Bicondicional com os 2 lados iguais = TAUTOLOGIA = frase sempre verdadeira.
Para testarmos se uma proposição é uma tautologia basta tentarmos fazer com que ela fique falsa, se não conseguirmos, ela será SIM uma tautologia.
No caso do conectivo ↔ (BICONDICIONAL), a proposição será verdadeira quando ambos os lados assumirem valores lógicos IGUAIS (VV ou FF).
Diante dessa constatação, se ao olharmos para a proposição BICONDICIONAL já conseguirmos ver que ambos os lados são iguais, tal proposição será SEMPRE VERDADEIRA, uma TAUTOLOGIA, portanto.
Espero ter ajudado.
Gabarito: Certo
Principais Regras:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
Não há necessidade de "testar" os valores.
Fórmula:
[(¬P)∨Q]↔{¬[P∧(¬Q)]}
Transformação (a negação da segunda parte está negando tudo o que vem depois):
¬ P v Q ↔ ¬ P v Q ----- ou seja, a mesma coisa!
Ou será as duas Falsas ou Verdadeiras, como a tabuada lógica da Bicondicional é "iguais é verdadeiro" só pode ser tautologia.
Quando a questão trouxer Bicondicional tente transformar as equações antes de testar os valores.
Outro jeito de resolver é perceber que a afirmação de que [(¬P)∨Q]↔{¬[P∧(¬Q)]} é tautologia nada mais é do que afirmar que (¬P)∨Q é equivalente a ¬[P∧(¬Q)], o que por sua vez é a mesma coisa de dizer que (¬P)∨Q é a negação de P∧(¬Q).
Estou acertando várias questões sem entender direito o assunto :(
Se tiver ↔ e perguntarem se é tautologia, olhe se as proposições são equivalentes (geralmente são). Se forem equivalentes = TAUTOLOGIA.
Minha contribuição.
Tautologia: VVVV
Contradição: FFFF
Contingência: VFVF
Abraço!!!
Quando o cespe pede esse tipo de questão, vc tem que sacar que é pra resolver com o mínimo de esforço possível.
[(¬P)∨Q]↔{¬[P∧(¬Q)]}
[P->Q] <-> ~ [ ~ (P->Q)] -negação da negação-
P->Q <-> P->Q
Considere a seguinte função booleana:
F = (~P).(~Q) + (~P).Q + P.(~Q )
Qual é a Tabela verdade que corresponde a essa função?
Letra C.
F = ((~P) v (~Q)) ^ ((~P) v Q) ^ (P v (~Q ))
Substitua o ponto pela disjunção e o sinal de mais pela conjunção, para ficar mais fácil sentencie com parênteses.
Faça a tabela verdade normalmente.
O número 1 equivale a falso e o zero equivale à verdade.
Matheus Andradae, resolve a sentença com as dicas da Juli Li.
Por fim, verifica qual é a coluna F que corresponde a conclusão da sentença: (~P).(~Q) + (~P).Q + P.(~Q ) => F F F V = 1 1 1 0
Letra C
Questão mal formulada. Quando se trata de booleano, 0 é falso e 1 é verdadeiro. Acho que no caso caberia recurso.
Pessoal, resolvi usando os operadores, tendo como base os valores de P e Q das tabelas das alternativas.
Depois de fazer as negações e resoluções multipliquei normalmente como está pedindo ( . ) e somei normalmente ( + ) como está pedindo a formula. Não é uma coisa complexa, afinal você só estará trabalhando com 0 e 1. Parece dificil mas é simples
Entendi da seguinte forma: reparem que todos os "P" e "Q" de todas as tabelas estão na mesma ordem.Então as negações invertem 0 para 1 e 1 para 0. Depois resolvi as multiplicações e depois somei. F= 1 + 0 + 0 = (1) / 0+1+0= (1) / 0+0+1= (1) / 0+0+0+ = (0)
Os valores entre parênteses são a resposta.Espero ter ajudado.
Pessoal para ajudar, é interessante estudar sobre os principios da Algebra Boolena. Abaixo 2 principios dessa teoria:
1. (A.B) + (A.B') = A
2. A + A'.B = A + B
A partir deste entendimento seguiremos os seguintes passos:
Passo 1: Aplica os principios da Álgebra Booleana na proposição F
F = (~P).(~Q) + (~P).Q + P.(~Q ) (Aplicar o principio nº 1 indicado acima)
=> F = ~ P + P.(~Q ) (Aplicar o principio nº 2 indicado acima)
=> F = ~ P + ~ Q (Observar que ~P e ~Q só podem assumir valor de Verdade, pois estão ligados pela conjunção "e")
Passo 2: Aplicando a tabela verdade considerando P = 0 (mentira) e Q = 0 (mentira) / ~P = 1(verdade) e ~Q = 1 (verdade)
# Temos que ~ P + ~ Q = ~ P ^ ~ Q <=> ~ (P v Q), logo:
P Q ~ (P v Q)
1 1 0
0 1 1
1 0 1
0 0 1
LETRA C
só consegui acerta essa parada quando descobrir que o PONTO é dijunção...
A cespe não aborda deste modo as alternativas.
LOGO o ponto é dijunção e o + conjunção
É o tipo de questão que assusta pelo jeitão dela, mas no fundo não é díficil.
não entendi
Agradeço pela explicação de Juli LI!
c)
+ representa OU (disjunção)
. represent AND (conjunção). Faz sentido se considerardmos que estamos trabalhando com n° binários (1 & 0).
1 + 1 = 1
1 + 0 = 1
0 + 1 = 1
0 + 0 = 0
Para conjunção é só considerar que qualquer valor vezes 0 = 0. Só é 1 quando for 1 * 1.
Pega os dados da tabela e substitua na equação normalmente, só que, quando for 1, a negação será 0 (e vice-versa).
O ponto é multiplicação e "+" é soma, faça como se fosse uma equação mesmo.
FONTE:
https://pt.wikipedia.org/wiki/%C3%81lgebra_booleana
operações binárias ∨ (também denotado por + é geralmente chamado de "ou")
e ∧ (também denotado por ∗ ou por . , é geralmente chamado de "e"
F= 0
v= 1
O professor Ivan chagas tbm havia comentado que + é uma disjunçao inclusiva "ou"
https://www.youtube.com/watch?v=ngqK_mtcaNo
questao Q548771 no qc
Ano: 2015
Banca: IBFC
Órgão: SAEB-BA
porém o professor Vinícius Werneck diz que + equivale a uma conjunçao.
Gostaria que os professores de matematica entrassem em consenso. Pois pra mim nao ficou claro, mas fiz a questao baseada pela fonte wikipedia
baseado nessas informaçoes nao concordo com o gabarito.
Só segui Juli Li:
F = ((~P) v (~Q)) ^ ((~P) v Q)) ^ ((P v (~Q ))
P/Q /~P /~Q /(~P) v (~Q) /(~P) v Q) /P v (~Q ) / ((~P)v(~Q))^((~P) v Q)) / ((~P) v (~Q)) ^((~P) v Q)) ^ ((P v (~Q ))
V V F F F V V F F
V F F V V F V F F
F V V F V V F V F
F F V V V V V V V
RESPOSTA:
0 0 1
0 1 1
1 0 1
1 1 0
A formatação retira os espaços que eu coloquei para frisar as colunas (coloquei as barras para ajudar).
Pessoal, vejam a explicação da professora, muito boa.
Fiz certo mas errei no final pois: comecei a tabela fazendo os primeiros valores como V, daí no final ficou trocado. Se tivesse me atentado nas alternativas antes de começar, teria já feito no modelo e acertado. o meu resultado deu contrário pois se tratava de uma pegadinha, pelo menos foi o que eu achei.
Dica: olhar as alternativas antes e começar a fazer a questão de acordo com o modelo de resposta que estão disponibilizando.
Nem acredito que acertei! A repetição leva a perfeição, mesmo que no caminho, haja erros...
(C)
Acertei depois de um bom tempo matutando nessa questão
Assinale a alternativa que contém a classificação correta para a proposição “Ao lançar-se uma moeda para cima, a face coroa cairá virada para cima ou não cairá virada para cima''
TAUTOLOGIA = resultado lógico é tudo V
- afirmação OU negação da afirmação(vice-versa) = TAUTOLOGIAPrezados colegas ,
P -> Q v ~ R .
Ao meu ver seria passivel de anulaçao,
Devido que seria uma CONTINGÊNCIA .
Explicado de forma simples por Joseph
P Q P v ~P
V F V
F V V
Tudo verdadeira então é uma Tautologia.
Bizuu
P V ~P = Tautologia
Afirmação OU negação da afirmação..
comentários excelentes...
A --> (B v ~B)
A -->
V
V
F
F
(B v
V
F
V
F
~B)
F
V
F
V
Resolvendo-se primeiro o que está entre parenteses, temos:
V
V
V
V
Agora, resolvendo-se a proposição A com esse resultado obtido das proposições entre parenteses, temos:
V
V
V
V
Certo. Tautologia.
P~P PV~P
VF V
FV V
“Ao lançar-se uma moeda para cima (P), a face coroa cairá virada para cima (Q) ou não cairá virada para cima (~Q)''
P = Ao lançar-se uma moeda para cima
Q = A face coroa cairá virada para cima
~Q = A face coroa não cairá virada para cima
P → (Q v ~Q)
P Q ~Q (Q v ~Q) P → (Q v ~Q)
V V F V V
V F V V V
F V F V V
F F V V V
Alguém sabe me esclarecer melhor e explicar todas as opções? eu agradeço
Quando todos os resultados possíveis de uma proposição composta forem verdadeiros, estamos diante de uma tautologia. Para isso, precisamos "desenhar" a tabela verdade e verificar todas as possibilidades. Na questão apresentada, todas as possibilidades de resultado são verdadeiras.
A tabela-verdade Se... Então (->) só admite resultado falso quando a segunda proposição é falsa e a primeira é verdadeira. A segunda proposição Q v ~Q será sempre verdadeira. Logo, todas as opções serão sempre verdadeiras.
Se todos os resultados forem falsos, teremos uma contradição.
Se os resultados forem falsos e verdadeiros, não importando a proporção entre eles, aí teremos uma contingência.
Pessoal, se montarmos a tabela-verdade não vai ser tudo verdadeiro, não. No resultado teremos V-V-V-V-F-F-V-V. Então, será uma contingência, porque para se montar essa tabela, como sabemos a quantidade de linhas? Devemos ver quantas proposições simples existem na questão. E, nesse caso, são três. Então é 2³=8.
O que estou achando é que a funcab desprezou a 1ª proposição e só considerou as outras duas. Se for assim, realmente temos uma tautologia, porque na disjunção inclusiva, se uma é verdadeira basta para que toda a proposição seja verdade.
Contradição
É toda proposição composta cujo resultado é todo falso.
Exemplo: Marcos Antônio é flamenguista e Marcos Antônio não é flamenguista.
BIZU
AFIRMAÇÃO e NEGAÇÃO DA AFIRMAÇÃO (VICE-VERSA) ⇒ CONTRADIÇÃO
Contingência
São proposições cujo os resultados não são todos verdadeiro nem todos falsos.
Exemplo: Renato é vascaíno ou Marcos Antônio é flamenguista.
Essa é simples:
Só há 2 proposições
P = Ao lançar-se uma moeda para cima a face coroa cairá virada para CIMA.
~P = Ao lançar-se uma moeda para cima a face coroa cairá virada para BAIXO.
TABELA VERDADE
_______________________________
P ~P P V ~P
V F V
V F V
F V V
F V V
_______________________________
Ou seja, é uma tautologia, pois no OU (V) só será falso se ambas forem falsas, o que não ocorreu.
Uma proposição e a sua negação ligadas pelo conectivo OU -> sempre será uma Tautologia.
Gabarito: B
Se tivesse princípio da identidade, juro que teria marcado. hehe
Se tivesse princípio da identidade, juro que teria marcado. hehe
Grande professor do Qconcursos, RENATO OLIVEIRA, muito obrigado mestre!
Considerando que, P, Q e R são proposições conhecidas, julgue os próximos itens.
A proposição [(P ∧ Q) → R] ∨ R é uma tautologia, ou seja, essa proposição é sempre verdadeira independentemente dos valores lógicos de P, Q e R.
Se na linha 2, caso vc fizer a tabela verdade , se o valor for V não podemos considerar a proposição como uma tautologia.
Errado
Errado
...
V F V V V V V V
Eu encontrei uma tautologia, alguem poeria mandar a tabela verdade para mim.
P Q R P^Q (P^Q) -> R [(P^Q) -> R] V R
V V V V V V
V V F V F F
V F V F V V
V F F F V V
F V V F V V
F V F F V V
F F V F V V
F F F F V V
Gabarito: ERRADO.
Não é uma tautologia, mas sim uma contingência.
P Q R P^Q (P^Q) -> R [(P^Q) -> R] v R
V V V V V V
V V F V F F
V F V F V V
V F F F V V
F V V F V V
F V F F V V
F F V F V V
F F F F V V
também substituí tudo por F e deu uma tautologia, estava tão feliz por descobrir este macete pratico, mas agora estou desconfiada. Lamentável.
gabarito:errado
para aqueles como eu que atribuem o valor "F" vimos que para algumas questões não funciona.
eu percebi que para questões curtas [(P ∧ Q) → R] ∨ R como essa não funcionava a tecnica, porem em questões gigantes
sempre deu certo.
então questões curtas façam a tabela!
É, também estava super feliz com as técnicas , mas pelo visto para garantir o ponto na prova ,
o melhor é fazermos a tabela verdade.. e torcer pra não aparecer questões demasiadamente longas..
mas não vamos desanimar , vamos focar em fazer essa tabela cada dia mais rápido!
assim poupamos tempo na hora da prova ;)
Para a Cespe todo "macete" tem sua exceção.
Quando falar "é sempre tautologia" e for de três proposições, pode fazer a tabela verdade que é mais confiável.
Esqueçam esse "macete" da F, as vezes é preciso perder tempo pra ganhar uma questão.
P Q R P^Q (P^Q) -> R [(P^Q) -> R] v R
V V V V V V
V V F V F F
V F V F V V
V F F F V V
F V V F V V
F V F F V V
F F V F V V
F F F F V V
P@#&@ porque não manda logo 5 proposições, ja que é pra %$##@# logo o candidato.
Gabarito : ERRADO
Pra economizar tempo: se perguntar se é uma Tautologia, basta atribuir o valor Falso como resposta. Se for possível o resultado dar Falso é porque a sentença NÃO pode ser uma tautologia.
[P ^ Q -> R ] V R
1ª parte Falso 2ª parte
Como observamos, trata-se de uma Disjunção. Para que uma disjunção seja falsa, só existe uma possibilidade: AMBOS os termos devem ser FALSOS, ou seja, a 1ª parte toda deve ser FALSA e a 2ª parte toda deve ser FALSA.
Agora analisando cada parte:
1ª Parte: trata-se de uma CONDICIONAL. Como ela deve ser falsa, só existe UMA possibilidade. Seu primeiro termo (P^Q) ser VERDADEIRO e o segundo termo (R) ser FALSO.
Sabendo disso, agora precisamos analisar a expressão P ^ Q. Para que P^Q seja verdadeira, somente se ambos termos sejam verdadeiros.
Dessa forma já sabemos que P é Verdadeiro, Q é verdadeiro e R é falso
2ª Parte: é o termo R, que já sabemos ser Falso.
Assim, observamos que essa sentença pode ter um valor lógico FALSO. Se existe essa possibilidade, é porque NÃO pode ser uma tautologia, que somente admite valor verdadeiro.
Parece ser complicado e demorado, mas não é. Que basta conhecer os conceitos básicos de cada sinal que da pra fazer muito mais rápido do que escrevendo a tabela da verdade.
Pessoal a moral é vc fazer a proposição ser falsa, entao é so atribuir o valor de F para o R e vai dar Vera fisher
[(P ∧ Q) → R] ∨ R ´
P VERDADEIRO COM P VERDADEIRO =VERDADEIRO
VERDADEIRO → FALSO= FALSO
R FALSO ∨ R FALSO = TUDO F DA F ENTÃO NÃO É TAUTOLOGIA
É recomendável e seguro fazer a tabela verdade. Existem questões que atribuindo F para todas as letras não dá certo.
Basta treinar a tabela e conhecer as regras dos conectivos. A maioria das questões não necessita preencher toda a tabela, a questão já é resolvida na segunda ou terceira linha.
GAB. ERRADO
Não entreguem a vaga de vocês ao método de atribuir valor F às proposições, procurem treinar a confecção da tabela-verdade para ganharem agilidade!
Pessoal é simples, basta atribuir os valores lógicos somente ao "R", pois no conectivo "ou" basta um dos lados ser verdadeiro, que toda a proposição será verdadeira, e se atribuirmos o valor de falso ao "R', independente do restante da questão será falso.
(....) v V= verdadeiro
(....)v F= falso
Logo, não é Tautologia
Gente, a lógica desse truque não é atribuir f à todas as proposições não.A lógica é tentar negá-la.Como vc falseia uma condicional? atribua valor falso ao R e Verdadeiro à conjunção que veio antes.Daí o todo será falso, depois faça disjunção ser falsa também, se vc conseguir tonar a proposição reduzida falsa, não é tautologia.
(p^q).....>R) v R
(V+V.....>F) v R
(F)v F
F
A galera entendeu mal essa coisa do F. Não é para atribuir F em todas as proposições.
DICA: Quando estiver resolvendo questões assim pedindo Tautologia, busque provar que é falsa. Se pedir Contradição, busque a verdade.
Por exemplo: temos [(P ∧ Q) → R] ∨ R
vemos que (P ∧ Q) → R formam uma condicional, daí eu pergunto pra mim mesmo. "O que faço para tornar uma condicional falsa?"
Que seja V se entao F = F. Viu só, eu não atribui falso a todo mundo. Então vai ficar assim:
(P ∧ Q) → R
V V F = F
Resolvendo Tudo, fica:
[(P ∧ Q) → R] ∨ R
V V F F = F
Logo a proposição [(P ∧ Q) → R] ∨ R não é uma Tautologia.
MANTENHA-SE FIRME! SEU NOME NO DOU.
Conseguir fazer esta tabela em três minutos...as vezes é melhor ir pelo caminho mais seguro, para ganhar uma questão na prova.
A proposição é falsa quando R = F:
[(P ∧ Q) → R] ∨ R
(V ^ V → F) v F
F v F
F
Nem precisa da tabela verdade pessoal. Como ele diz que será sempre verdadeira(tautologia) é só testar com falso dos dois lados (pois as preposições estão unidas por uma disjunção(OU) e será falsa quando os dois lados forem falsos). Voce ve que ira depender dos valores de P e Q para a proposição acima ser verdadeira. Dificilmente a Cespe vai querer que o candidato monte uma tabela verdade na hora da prova.
Errada
Resposta: V F V V V V V V
P Q R P^Q (P^Q) -> R [(P^Q) -> R] v R
V V V V V V
V V F V F F
V F V F V V
V F F F V V
F V V F V V
F V F F V V
F F V F V V
F F F F V V
Errado!!
https://www.youtube.com/watch?v=8irXP1JjgIQ&t=7s - A MELHOR EXPLICAÇÃO SOBRE TAUTOLOGIA QUE JÁ TIVE. VALE A PENA.
Acabei de descobrir que o " F " é um macete que nem sempre dá certo...
Esse macete é furada! Tive a mesma surpresa, amigo.
ERRADO
[(P ∧ Q) → R] ∨ R = F
V ∧ V = = F
V → F = = F
F ∨ F = F
se deu certo então não é uma tautologia
essa macete de atribuir f em todas só da certo quando for proposição bicondicional. PS: pelo menos todas q eu fiz de bicondicional deu certo.
só uma malandragem de agilidade, se vc vir que dentro da condicional tudo é diferente, é óbvio que tem como ser falso ou verdadeiro, basta olhar o resto pra ver se muda.
Essa nem precisa fazer tabela nem macete, o cespe afirmou que seria (sempre verdadeira),ou seja, uma tautologia, independentemente dos valores lógicos, é claro que isso não procede, pois se vc mudar um valor pra falso, não será mais tautologia.
Gab ERRADO.
Se no " OU ", só é F se todas forem F, e o candidato definir o R como verdadeiro, já invalida a questão.
Errado, façam a tabela verdade, no final dará 9 V e 1 F ou seja, trata-se de uma contingência. Tautologia é quando no final da tabela todos os valores são " V "
Errado.
A quantidade de linhas de uma tabela-verdade se relaciona com a quantidade de proposições.
[ (P ∧ Q) → R ] ∨ R [
(V e V ) → F ] ou F
[ V → F ] ou F
F ou F : F
Questão comentada pelo Prof. Márcio Flávio
[(P^Q) -> R] v R
[(F^F) -> F] v F
[V -> F] v F
F v F = F
Se deu falso não é caso de tautologia!
Resolvemos questões que pedem para Tautologia da seguinte forma: buscamos provar que é falsa. Se pedir Contradição, busque a verdade.
Temos [(P ∧ Q) → R] ∨ R
Vimos que (P ∧ Q) → R formam uma condicional, logo, eu me pergunto: "O que faço para tornar uma condicional falsa?"
Vera Fischer é Falsa, ou seja, que seja V então F = F.
Então, vai ficar desse modo:
(P ∧ Q) → R
V V F = F
Resolvendo Tudo, fica:
[(P ∧ Q) → R] ∨ R
V V F F = F
Logo, percebe-se que tentamos provar que era falsa e conseguimos. Se eu consigo provar que é falsa, então não pode ser Tautologia como afirma a questão. Se eu não tivesse conseguido prova que essa proposição é falsa, então realmente seria Tautologia. Logo, a proposição [(P ∧ Q) → R] ∨ R não é uma Tautologia e está errada.
eu figuei na quela mais fui marca e certa mais no casa e a verdadeira e errada pq eu pensava que todas que fosse v era verdadeira tambem tinha muito calculo ai agente terme na basi
essa forma de logicas para palavra que com funde muitos as pessoas quando fala en calculo ai ja ven uma resposta certa
Fazendo a tabela verdade é possível verificar que, não se trata de uma tautologia:
P Q R P/\Q (P/\Q)->R (P/\Q)->R \/ R
V
F
V
V
V
V
V
V
Explicando de forma simples: Se P ou Q for verdadeiro e R for falso, a Proposição se torna FALSA! Pois a condicional ficará falsa, consequentemente, a Dijunção tbm ficará FALSA.
Questões como essa nem sempre é uma boa fazer a tabela da verdade, pois pode ser que você perca muito tempo. Tente atribuir valores lógicos nas proposições para que ela fique FALSA quando a questão afirmar que seja uma tautologia, caso seja possível atribuir valores sem nenhum tipo de absurdo para que a proposição fique FALSA, então quer dizer que a proposição realmente não é uma tautologia.
Se aparecer um V então F será falsa( vera fischer) . Tautologia implica em ser verdadeira qualquer que seja o valor logico das proposições.
GABARITO ERRADO
Tabela verdade funciona, mas é bem mais demorado. Prefiro usar um método simples, rápido e seguro: atribuir valor FALSO à proposição. Se conseguir através dos outros valores tornar a proposição FALSA, não será tautologia.
Minha contribuição.
Tautologia = VVVV (sempre verdadeiro)
Contradição = FFFF (sempre falso)
Contingência = VFVV (Há um misto de V e F)
Abraço!!!
A dica é:
Para ser tautologia, os elementos da 'esquerda' tem que ser os mesmos da 'direita'. Se não tiver, então pode descartar ser tautologia.
Exemplo:
P e Q ou R -> P e Q e R. (não sei se é tautologia)
Mas se aparecer
P e Q ou R -> P ou Q com certeza não é tautologia pois precisa ter o R para poder testar.
Resolvi sem tabela-verdade.
Tente julgar a alternativa como F, se der, o gabarito será "Errado".
Por exemplo, atribua F para todas as proposições abaixo e veja se dará uma tautologia:
[(P ∧ Q) → R] ∨ R = Falso.
Comece atribuindo F ao R e tente induzir as outras proposições ao famoso "Vera Fisher". Se você conseguir, é sinal de que não é uma tautologia.
Conseguiu?
GAB: E.
ERRADO
Consegui deixar falsa, então está longe de ser uma tautologia.
Vamos considerar o seguinte:
P:V
Q: V
R: F
[(P ^ Q) -> R] v R
[(V ^ V) -> F] v F
[V -> F] v F
F OU F: F
2021: um ano de vitória.
Gabarito: Errado.
A questão fala em adotar valores lógicos independentes de que sejam V ou F. Devemos nos ater a última proposição, na qual o conectivo é uma disjunção inclusiva (v): [(P^Q) -->R] v R. Se adotarmos que R seja F e que P e Q seja V, ao final teremos valor F: [(P(V) ^ Q (V)) --> R (F)] v R (F). Resolvendo os parênteses teremos um valor V (V ^ V = V). Resolvendo os colchetes teremos um valor F [ V --> F = F], logo o valor F (fora dos colchetes) com a disjunção OU (v) seguida de R, este sendo F teremos F v F = F. Não sendo, portanto, uma tautologia.
Resolver pela tabela verdade é mais seguro, porém se vierem mais de 3 proposições é melhor resolver provando que é falso.
------------------------------------------------------------------ATENÇÃO------------------------------------------------------------------------
ESSA QUESTÃO PROVA QUE O MACETE QUE ALGUNS ANDAM FALANDO POR AÍ NÃO FUNCIONA: COLOCAR TUDO "F".
Gabarito: Errado
Principais Regras:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
Bizu!
tente tornar a proposição "F", se for possível não será Tautologia !
[(P ^ Q) ---> R] v R = F só será F no conectivo ----> (se então) se for Vera Fischer (V ---> F) !
....................... v ... = F aqui vc identifica como é possível ficar F levando em conta o conectivo !
F v F = F no conectivo v (ou) será possível quando P for F e Q for F !
F o resultado foi F então não se trata de uma Tautologia ! Dica do grande Professor Jhony Zini. Abraço!!
Não perdi tempo tentando resolver a questão. Não tem preposições iguais, logo não pode ser uma tautologia.
Maria está escrevendo uma mensagem a ser enviada por e-mail. Um dos trechos da mensagem traz a seguinte proposição: “Beatriz comprou um carro novo ou não é verdade que Beatriz comprou um carro novo e não fez a viagem de férias”.
A partir dos seus conhecimentos, pode-se afirmar que a única alternativa correta é:
O caso é de tautologia, não importa o valor lógico das proposições, a expressão será verdadeira. Isso acontece pois:
B v ~(B ^ V) .: B v (~B v ~V)
Numa disjunção, basta que uma das afirmativas seja verdadeira para que a expressão inteira o seja.
Espero ter ajudado.
Bons estudos!
quebrei a cabeça e não consegui entender... fiz a tabela e não cheguei a tautologia. Alguém pode ajudar?
Eu montei a expressão da seguinte maneira:
B v (~B ^ ~V)
Se alguém puder me explicar o motivo pelo qual está errado minha montagem, agradeço! =D
Larissa, a sua segunda expressão está equivocada.
O certo seria: P v (~Q ^ ~R).
Eu também montei a tabela verdade e não cheguei a tautologia.
Boa tarde Senhores!
Luciano a expressão da Larissa está correta visto que devemos interpretar da seguinte forma: "Não é verdade que Beatriz..."
Não é verdade que = ~
Dessa forma teremos: B v ~ (B ^ ~V)
Ao negar: (B ^ ~V), trocam-se os sinais e inverte o sinal, teremos então: (~B v V).
Luiz e Tatiane, espero ter contribuído para o entendimento de vocês.
Bons estudos!
Ainda não consegui entender :( alguém me ajuda por favor!
Essas bancas de prova de prefeitura, só uma força maior pra suportar isso.
Tentar contribuir o ensino do colega abaixo:
Bom preste atenção na montagem da proposição composta.
"Beatriz comprou um carro novo" = P;
"ou"= V
"não é verdade que" = ~ (preste atenção o erro pode está aqui neste entendimento. Essa negação, nega toda a próxima conjunção)
"Beatriz comprou um carro novo e não fez a viagem de férias"= (P^~Q) (considere Q= viajou e ~Q= não viajou.
Respire... Montemos agora com as informações acima:
P v ~(P^~Q) (Observe que temos uma negação da conjunção P^~Q)
resolvendo a negação temos: P v (~P v Q)
Jogue isso na tabela para confirmar uma tautologia.
Espere ter ajudado...
P = Beatriz comprou um carro novo
~P = não é verdade que Beatriz comprou um carro novo
~Q = não fez a viagem de férias
Montando a proposição acima :
P v ( ~P ^~Q)
V v (F ^ F)
F v (V ^ V)
Resolvendo
V v ( F ) = V
V v ( V ) = V TAUTOLOGIA
Minha dificuldade é saber onde colocar os parênteses.
Consegui acertar a questão, pois utilizei a ideia do OU (disjunção), mas gostaria de saber fazer o cálculo.
Obrigada, Salmir Oliveira, muito obrigada! Eu não tinha negado toda a proposição, já ia me enforcar, mas você me salvou.
A NEGAÇÃO DA CONJUNÇÃO É A DISJUNÇÃO COM O P E Q NEGATIVO:
P = BEATRIZ COMPROU UM CARRO NOVO
~P = NÃO É VERDADE QUE BEATRIZ COMPROU UM CARRO NOVO
~Q = NÃO FEZ A VIAGEM DE FÉRIAS
P v ( ~ P v ~ Q )
V V F F F
V V F V V
F V V V F
F V V V V
A NEGAÇÃO DA CONJUNÇÃO É A DISJUNÇÃO TROCANDO O P ^ Q POR ~P v ~Q, LOGO O RESULTADO DARÁ UMA TAUTOLOGIA.
VAMOS RESOLVER
PRIMEIRO
P Q
V F
F F
V V
F V
RESULTADO DE P e ~Q
V V V
F V F
V F F
V F F
NEGATIVA DE P e ~Q
F
V
V
V
RESULTADO DE P V (P e ~Q)
V F V
F V V
V V V
F V V
RESULTADO FINAL >>>> TAUTOLOGIA
desculpe o tamanho tentei fazer do modo mais simples possivel
Pontos pra Salmir Oliveira. Valeu mesmo!
ajudou bastante a explicação de Salmir Oliveira
Cade a explicação em video? Se ler adiantasse nao estaria nessa ferramenta
Não gostei do comentário escrito do professor, além de ficar muito desorganizado o entendimento não é o mesmo se realizado em
vídeo.
Também prefiro que os comentários do professor seja em vídeo, pois fica mais claro pra entender .
Por favor, explicação em vídeo!!!!
P Q ~P (~PvQ); Logo: P v (~PvQ)
V V F V V
V F F F V
F V V V V
F F V V V
P: Beatriz comprou um carro novo
Q: Beatriz fez a viagem de férias
~PvQ: negação de P^~Q
Galera, um bizuzinho para identificar tautologia só com uma piscada:
Afirmação ou negação da afirmação (vice-versa)
Afirmação negação da afirmação
“Beatriz comprou um carro novo ou não é verdade que Beatriz comprou um carro novo e não fez a viagem de férias”
Gabarito: Alternativa A
“Beatriz comprou um carro novo ou não é verdade que Beatriz comprou um carro novo e não fez a viagem de férias”.
Beatriz comprou um carro novo ( B ); não é verdade que Beatriz comprou um carro novo ( ~B) não fez a viagem de férias (~N ).
B ~N ~B N B ^ ~N ~(B ^ ~N) B v ~(B ^ ~N)
V V F F V F V
V F F V F V V
F V V F F V V
F F V V F V V
Como todos os valores da proposição final são verdadeiros, trata-se de uma tautologia.
Larissa Nascimento, eu acredito que a proposição é montada desta maneira porque para o correto preenchimento de uma tabela verdade, devemos seguir algumas regras e uma delas é que devemos fazer primeiro as conjunções, em seguida as disjunções, depois os condicionais e por último os bicondicionais. Acho que é por isso.
Bons estudos a todos.
Comprou um carro = P
Viajou = Q
Vamos resolver por partes. Primeiro vamos ver como fica a parte (beatriz comprou um carro novo e não viajou). Eu sei que ela quer a negação, mas podemos começar apenas pela analise da proposição, depois a gente nega (principalmente quem não conhece equivalência e negação). Vamos lá:
P Q (~Q - inverte o Q) P ^ (~Q)
v v f f
v f v v
f v f f
f f v f
Temos o seguinte para a primeira tabela: f v f f. Como a questão quer o "não é verdade", temos que negar esse resultado, para isso invertemos os valores, vai ficar assim: v f v v.
P Q (~Q - inverte o Q) ~( P ^ (~Q))
v v f v
v f v f
f v f v
f f v v
Agora devemos fazer o P (comprou o carro) OU o resultado acima (negação do comprou carro e não viajou)
P Q (~Q - inverte o Q) ~( P ^ (~Q)) P V ~( P ^ (~Q))
v v f v v
v f v f v
f v f v v
f f v v v
A tabuada do OU é tudo F dá F; ou seja se tiver um v em qualquer coluna o resultado vai ser V.
Questãozinha que parece que é simples mas dá um trabalhinho, porque você trabalha mais do que pensa. Com as duas possibilidades, precisa-se encontrar 4 resultados diferentes.
Essa questão foi realizada pela FUNDATEC EM 2012 e deu o que falar, mas não resta dúvida que é uma TAUTOLOGIA. Ela precisa de um pouco de atenção.
Gente,
A proposição se monta da seguinte forma: p v ~(p^q). Nesse sentido, qualquer valor que você atribua as premissas o resultado será sempre verdadeiro (tautologia).
Obs: o que confunde na questão é montar do seguinte modo: p v (~p^q)
Espero ter ajudado.
A representação da proposição composta fica assim: P v ~ (P ^ Q)
A partir dae basta fazer a tabela verdade e descobrir que o valor lógico é uma Tautologia.
Considere as afirmações abaixo.
I.O número de linhas de uma tabela-verdade é sempre um número par.
II. A proposição " ( 10 < √ 10 ) ↔ ( 8 - 3 = 6 )" é falsa.
III. Se p e q são proposições, então a proposição “(p → q) ∨ ( ~ q)” é uma tautologia.
É verdade o que se afirma APENAS em
não entende por que a III está incorreta.
A III não está incorreta, a questão pediu as afirmações verdadeiras, portanto, a I é verdadeira pq o número de linhas de uma tabela verdade é sempre par e a proposição da III é verdadeira pq é uma Tautologia (resultado td verdadeiro).
Alternativa E correta
Item I, CERTO, pois para determinar o número de linhas de uma tabela verdade usamos a formula 2 , e esta formula gerará sempre um número par.
Item II, ERRADO, pois FF gera uma frase verdadeira
Item III, CERTO. É SÓ FAZER A TABELA, QUE DÁ TUDO VERDADE!
FONTE: http://www.cursoaprovacao.com.br/investidor/arquivos_antigos/Prova%20comentada%20do%20ICMS%20SP%202006%20(rac,%20inf,%20e%20est).pdf
Penso que o item II esteja incorreto por não ser uma proposição o seguinte termo: (8 - 3 - 6). Como posso falar se isso é verdadeiro ou falso?
P>>Q= VFVV
~Q= FVFV
III - quando tem o OU = VF, FV, VF, VV= VVVV tautologia, são todas verdadeiras.
A III está correta é uma tautologia. a primeira parte resulta em FVVV e a segunda VFFV. Ao fazer a análise com OU (v) todas são V.
Tautologia: Quando todos os resultados finais da tabela verdade resultam em V;
Contradição: Quando todos os resultados finais da tabela verdade resultam em F;
Contigência: Quando temos tanto V como F nos resultados finais da tabela verdade.
1)CERTA todo mundo sabe disso.. O numero de linhas da tabela verdade é sempre par.. pois 2^n, pode ser sempre 2 elevado ao quadrado ou ao cubo, enfim... O resultado sempre dará um numero PAR.
2) ERRADA ,está errada pois a regra do ↔ (se somente se) sempre será VERDADEIRA EX: (v + v= v) (F+F=V), e a questão coloca um ↔ e diz q é falsa, matou a questão como errada! não precisa nem fazer cálculo.
3) CERTA, dá uma Tautologia= todos os resultados são verdadeiros.
vejamos:
p q (p → q) v (ou) ( ~ q)
V V V F = v
V F F V = v
F V V F = v
F F V V = v
Antonio Lino , a III não está incorreta .
sera que alguem pode me ajudar na II pois nao a vejo como proposição. tipo nao consigo julgar 8-3-6 o que tem 8-3-6? tipo eles deveriam dizer se e se soment se 8-3-6 igual ou menor a alguma coisa. penso eu. se eu estiver errada, alguem pode explicar melhor?
Pessoal,
Na afirmação II contém um pequeno erro.
Resolvi a mesma questão em materiais e quando a vi aqui pesquisei para averiguar.
O fato é que em vez de (8 - 3 - 6) seria (8 - 3 = 6).
Não vai alterar o gabarito visto que continua sendo falsa mas já serve para tirar qualquer dúvida.
I - Número de linhas é potência de 2 , portanto par.
II- F<--> F <==> V
III- ( P-->Q ) v ¬Q P--> ( Q v ¬ Q ) P --> V <==> V ;Tautologia
Ahh!! Considerando que houve um erro de digitação e que deveria ser (8 - 3 = 6), como alguns colegas falaram, passa a fazer sentido que seja F!!
I - CERTO
FÓRMULA: 2^n
_________________________________
II - ERRADO
√10 = número entre 3 (√9) e 4 (√16)
(10 < √10) ↔ (8 - 3 = 6)
(____F____) ↔ (____F___)
VERDADEIRO
_________________________________
III - CERTO
(p → q) v (~q)
V____V____F
V____F____V
F____V____F
F____F____V
(p → q) v (~q)
___V_______F
___F_______V
___V_______F
___V_______V
(p → q) v (~q)
________V_____
________V_____
________V_____
________V_____
TAUTOLOGIA
AFIRMAÇAO I ( VERDADEIRA ) - Os números de linhas de uma tabela verdade sempre vai ser par , pois ela se dá pela multiplicação do numeral 2 . sendo 2 n , n o numero de preposições. sendo que sempre o resultado irá ser um numeral par. Ex: 2²= 4 ou 2³=8
AFIRMAÇÃO II ( FALSA ) - RAIZ QUADRADA DE 10 É MENOR QUE 10 E NÃO MAIOR QUE 10. Afirmação falsa ( 10 > raiz de 10 ) que seria a afirmação verdadeira . neste caso F <-> F= V
sendo <-> iguais da Verdadeiro e diferentes da falsa .
AFIRMAÇÃO III ( VERDADEIRA ) = (V v F = V ), (F v V = V ), (V v F = V ), (V v V = V ) É UMA TAUTOLOGIA
Reposta correta letra ( E )
A única diferença da LC e da LO é o quórum (aquela de maioria absoluta) e que a LC trata sobre matérias que estão previstas pela Constituição Federal e a LO pode tratar sobre qualquer matéria que não seja reservada a LC ou outra espécie normativa.
LC não regula matérias mais relevantes, ela regula o que o constituinte determinou. (Por exemplo, o orçamento público é uma matéria relevante, e é regulada por lei ordinária).
Seja a sentença ~{[ (p → q) ∨ r] ↔ [q → (~p ∨ r)] }.
Se considerarmos que p é falsa, então é verdade que
sendo p falsa:
(p->q) = F-> V = V ou F->F = V Logo o valor da expressão (p->q) ,independente do valor de q, sempre vai ser sempre V.
(~p-> v r) = V v V = V ou V v F = V logo o valor da expressão (~p v r), independente do valor r, sempre vai ser sempre V.
{(p->q) v r } sabendo que o valor da expressão (p->q) sempre será V, independente do valor de r, a expressão vai ser tbm sempre V.
{q->(~p-> v r)} sabendo que o valor da expressão(~p-> v r) sempre será V, independente do valor de q, a expressão vai ser tbm sempre V.
[(p->q) v r } <->{q->(~p-> v r)] = logo V <-> V = V
~[{(p->q) v r } <->{q->(~p-> v r)}] = com a negação fica F.Gostaria que alguém me explicasse o porquê de a letra "b" também não estar correta.
Grato!
Olá Andrade!
Essa questão foi anulada por essa confusão com a letra B.
beleza a d está certa...mas no vejo motivos para a b está errada. A não ser que a frase da "b" "essa sentença", esteja se referindo a qualquer valor de p (v ou f), ou seja sentença toda. Mas isso seria uma incoerência com o próprio enunciado.
A princípio a questão não foi anulada, pois pesquisei e não encontrei essa anulação. No site fcc não existe mais o histórico dessa informação e nos demais sites a questão não está como anulada.
Ai não sei...Fica a dúvida.
Fazendo o teste para P = v, Q = f, R = f (1 das 4 possibilidades) a sentença será V, negando o item b.
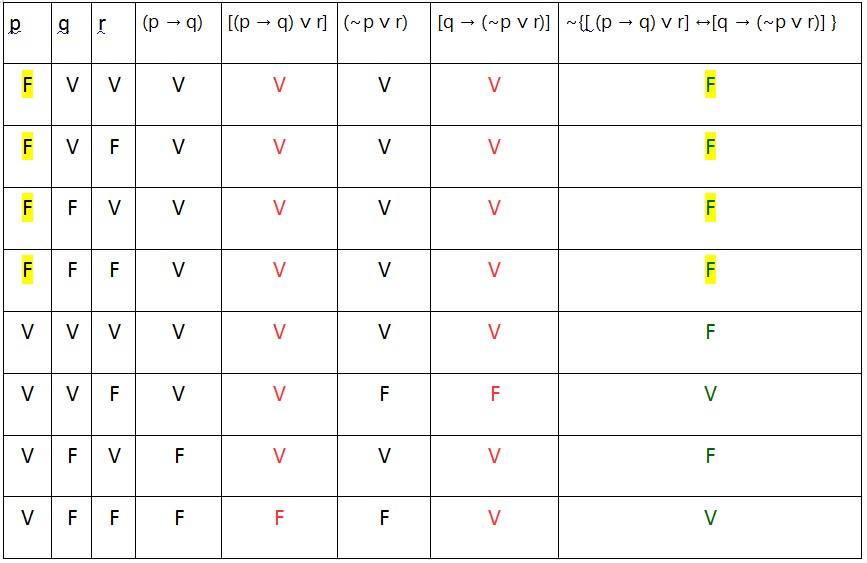
preciso da ajuda de um professor nessa
Questão complexa, porém percebi que há duas alternativas que se equivalem de acordo com a reposta da tabela verdade,
C e D , ou seja, há dois valores, verdadeiros e falsos, pois tautologia não é e eu tenho p FALSO - FALSO e P falso = verdadeiro no resultado final.
tenso
Eu também cheguei neste resultado VICTOR VITORIANO, até me tocar do sinal de negação (~) antes da proposição inteira... com este sinal tudo se inverteu, e a resposta passou a ser a letra D. Espero ter ajudado
Força! Sempre!!!
"Essa questão foi anulada, muito provavelmente pela confusão de resposta com a letra B. Analisando friamente, concordo com anulação, porque foi dito no enunciado que era falsa. Partindo dessa premissa, pode-se afirmar que o valor lógico da sentença é sempre F. Mas cuidado! Em prova de concurso, marque sempre a mais certa! Neste caso, a mais certa é a letra D."
FONTE: Prof. Felipe Lessa - Estratégia.
quero varias dessa!
Pessoal, olhei no site da FCC e no arquivo no qual constam as atribuições de questões e alterações de gabarito, não há menção à essa questão. Logo, a questão não foi anulada e o gabarito NÃO foi alterado; a resposta é mesmo letra d) nas linhas da Tabela-Verdade em que p é F, a sentença é F.
Eu consegui fazer a tabela verdade e comprovar que a letra d está certa, mas também não entendo por que a letra b não é correta.
Essa questão foi anulada sim!
Gabarito comentado pelo Profº Vítor Menezes:
Letra A: a sentença não é tautologia. Vimos que seu valor lógico é F. Uma tautologia apresenta apenas valores lógicos V.
Letra B: de fato. dado que p é falso, a proposição assume sempre o valor lógico F, independente do valor lógico de "q" e "V". Alternativa correta.
Letra C: como vimos acima, quando p é falso, a proposição composta é falsa. Alternativa errada.
Letra D: de fato, quando p é falso, a proposição composta é falsa. Alternativa correta.
Letra E: Se levarmos a redação da questão ao pé da letra, a alternativa estaria correta. Ela apenas afirma que não foram informados os valores lógicos de q e r. Isso realmente não foi informado.
Aparentemente, a alternativa quer dizer que, para concluirmos qualquer coisa sobre a proposição composta, seria necessário conhecer o valor lógico de q e r. Isto está errado. Vimos que, dado que p é falso, a proposição composta é falsa, independente dos valores lógicos de q e r.
Há mais de uma alternativa correta. A questão foi anulada.
Se P e Q forem V e R for F então a sentença é V. A letra B está errada.
Vitor paulo, o enunciado diz claramente que p é falsa.
Na verdade a alternativa (e) também é verdadeira, porque o valor de q e de r não foram informados..
Como podem elaborar uma questão tão imbecil? Se a questão afirma um valor, por que colocar de novo como hipótese nas respostas?
Vejam o comentário da Kelly Lobão.
Pessoal,
Fiz com a tabela da verdade, acertei, mas alguém tem uma maneira mais fácil de fazer? (afinal de contas se cai uma dessas na prova e eu for montar a tabela perderei muito tempo)
Peço a gentileza que coloquem de maneira bem clara, pois estudo RL a pouco tempo e não tenho muita habilidade!
VICTOR VITORIANO, caí na mesma cilada que você. Esqueci completamente o sinal de negação.
Olhando apenas para a sentença:
P -> Q é verdadeira, pois P é falsa e uma condicional para ser falsa tem que ser P verdade e Q falsa.
P -> Q v R verdadeira, pois na disjunção basta que uma seja verdade para a sentença ser verdadeira.
~P v R verdadeira e nesse caso P é verdade, mesmo caso de disjunção acima.
Q -> (~P v R) verdade, condicional só é falsa se a segunda proposição for falsa.
Se tudo é verdade, então a bicondiconal <-> é verdadeira.
MAS, no começo aparece ~ que nega tudo, então a sentença será falsa. Dando choque entre B e D.
Observe que, se p for F, podemos afirmar que a condicional pq é V. Com isto, a disjunção
certamente é V. Por outro lado, ~p será V. Com isso, a disjunção
certamente é V, de modo que a condicional
também é V.
Pelo que vimos acima, a bicondicional é V pois ela tem os valores lógicos
. E a negação desta bicondicional, isto é,
, é Falsa.
Isto nos permite afirmar que, quando p é F, a sentença é F. Temos isto na letra A.
Resposta: D
Considerando as seguintes proposições,
p: A união de conjuntos é comutativa e a diferença de conjuntos é associativa.
q: 2 + 3 = 6 ou 3 . 2 = 6.
r: A capital de Alagoas é Maceió ou o Brasil é uma ilha.
os valores lógicos de p, q e r são, respectivamente
gab E
p: A união de conjuntos é comutativa e a diferença de conjuntos é associativa.
comutativa, a ordem não altera o resultado
associativa, não sei explicar, mais é falso
E tudo V dá V, como tems VF, será FALSO
q: 2 + 3 = 6 ou 3 . 2 = 6.
"OU , tudo F da F" , como temos um FV será VERDADE
r: A capital de Alagoas é Maceió ou o Brasil é uma ilha.
"OU , tudo F da F" , como temos um VF será VERDADE
A propriedade associativa dá ideia de soma, por isso a diferença de conjuntos não é associativa.
A propriedade associativa diz respeito à possibilidade de se mudar a sequência da operação sem que isso altere o resultado. Ex.: (2.3).5 = 2.(3.5). Dessa forma, é falso que a diferença de conjuntos seja associativa, uma vez que (A - B) - C não é o mesmo que A - (B - C).
RESPOSTA E
Comutativa: A U B = B U A
Associativa: (A U B) U C = A U (B U C)
#sefaz.al2019 #ufal2019
p: A união de conjuntos é comutativa e a diferença de conjuntos é associativa.
p: V ^ F = F
A conjunção (^/e) para que seja Verdadeira, todas as preposições têm que ser Verdadeiras.
q: 2 + 3 = 6 ou 3 . 2 = 6.
q: F v V = V
A disjunção (v/ou) para ser verdadeira, basta que uma das preposições seja verdadeira.
r: A capital de Alagoas é Maceió ou o Brasil é uma ilha.
r: V v F = V
A disjunção (v/ou) para ser verdadeira, basta que uma das preposições seja verdadeira.
GABARITO: E
Em relação aos argumentos seguintes,
I. p → q, ~q | ______ p
II. p → q, q → r | ______ r
III. p ∨ q, q | _____ p
temos que
Não entendi bulhufas, alguém conseguiu e pode explicar?
Eu substituo os sinais por frases, na minha cabeça fica mais fácil de analisar.
Segue:
I. p -> q (Imagino, se Juiz (p) -> então advogado (q)).
~q Ele não é advogado
p Então ele é juiz.
Resposta: Ele não é juiz, argumento inválido, já que para ser juiz, ele teria que ser advogado antes.
II. P -> Q (Se juiz, então advogado)
q ->r (Se advogado, então passou na OAB)
r (Então passou na OAB).
Argumento inválido, nada garante que ele passou na OAB, não podemos concluir nada de r.
III. P ou Q (Ou nasceu em Alagoas ou em Pernambuco)
Q Nasceu em PE
Então é inválido, porque ele conclui P, que na nossa frase é nasceu em Alagoas, e já concluímos que ele não nasceu nesse estado.
Pra mim funciona assim.
Nesse tipo de questão a melhor coisa a se fazer é desenhar tabela verdade de todas as premissas e analisar as linhas onde elas são verdade se a conclusão for verdade em todas o argumento é válido se houver pelo menos uma falsa ele é inválido.
Ex .III
P v Q | Q | P
V V V
V F V
V V F * conclusão falsa argumento inválido
F F F
que merda significa isso: | ------
Isto '| ------ ' significa algo do tipo Conclusão.
Referencia: Raciocínio Lógico- Bruno Villar
GABARITO: A
fiz tabela verdade e bateu.
Para a questão , foi adotada a seguinte notação: v significando disjunção; ʌ significando conjunção; ¬ significando negação, V significando verdadeiro e F significando falso, “p" significando um exemplo de proposição e “q" significando um exemplo de proposição.
Assinale a alternativa que apresenta, correta e respectivamente, os valores de verdade faltantes nas células 1, 2 e 3 da tabela-verdade mostrada a seguir.
p q ¬p ¬q
V V 1 3
V F F V
F V 2 F
F F V V
Alternativa A
Se a coluna P é V, V, F,F sua negação será F, F, V, V
Se a coluna Q é V, F, V, F sua negação será F, V, F, V
Resposta: 1 -F 2- V 3-F
questão mamão..
observem: tudo nessa questão depende do modificador ¬ (não), se a proposição P é verdadeira, ¬P será falsa.. ou vice versa
a mesma coisa acontece com o Q.. sendo assim na tabela dar pra saber quais sao sua posiçoes e valores..
Gurdurinha.
Realmente a questão é fácil, mas se não prestar atenção na sequência que o examinador pede o candidato erra.
F, V e F -> Gabarito [A]
de onde saiu que o 2 é V?
Dayana, observe somente a linha em que está o nº 2. Se naquela linha p é F, então ¬p(2) é V.
p q ¬p ¬q
V V F F
V F F V
F V V F
F F V V
FVF - GAB A
Quebrei a cabeça pra entender que a questão era muito fácil! Achei que estava faltando algum dado.Confesso que fiquei chocada!
Os caras fazem uma questão TODA bagunçada para parecer difícil... "Malandramente"...
Putz ... não consegui nem entender para tentar responder.... :(
questãozinha safada
Questão super fácil, esta pedindo para negar a coluna.
P ~P Q ~Q
V F V F
V F F V
F V V F
F V F V
LETRA - A
A pegadinha está que na sequêcia em que vc analisa a questão, os números são: 1,3,2, e depois ela pede a sequência 1,2,3.
Questão simples, porém quase que eu erro rsrs
P ~P Q ~Q
V F V F
V F F V
F V V F
F V F V
letra a
A questão tentou ser sacana colocando o 3 ao lado do 1.
kkkk
Se caísse só dessas eu estaria feliz
Isso nunca mais vai cair....
OBS: respectivamente.
kkkk! É sério que caiu uma questão dessa? A pessoa que elaborou essa questão estava com muito sono.. hahaha!
GAB: A de Abelha
p q ¬p ¬q
V V F F
V F F V
F V V F
F F V V
F, V, F
Pode ter certeza,mesmo uma questão desse modo que é considerada muito fácil até mesmo pelo filtro do qc,quebra uns 50% de candidatos que não estudaram nada.
tava tão na cara que fiquei com medo de marcar a A.
a questão é simples, ele apenas pede para NEGAR o valor lógico de P e de Q. onde está F fica V e onde está V fica F
cuidado com o "respectivamente" ele te derruba, caso não o considere.
Fiz o calculo certinho mas não me atentei a ordem 1,2 e 3, errar aqui pra acertar na prova!
esse tipo de questão são as mais fácil.. haaaa se todas fossem assimm.
Respectivamente é a chave.
São as mais ¨fácil¨...
Não consegui ver por que a segunda opção foi V
Se as questões fossem todas assim, estava bom demais :)
Se as questões fossem todas assim, estava bom demais :)
muito fácil, porém buga a mente. KKKKKKKKKKKKKK
Para a questão , foi adotada a seguinte notação: v significando disjunção; ʌ significando conjunção; ¬ significando negação, V significando verdadeiro e F significando falso, “p" significando um exemplo de proposição e “q" significando um exemplo de proposição.
Considerando a tabela-verdade apresentada, assinale a alternativa correta.
p ¬ p p v ¬p
V F V
F V V
Letra B
Tautologia - apenas resultados V.
Contradição é uma proposição cujo valor lógico é sempre falso.
Tautologia é uma proposição cujo valor lógico é sempre verdadeiroContingência = Quando uma proposição não é tautológica nem contraválida, a chamamos de contingência ou proposição contingente ou proposição indeterminada.
Tautologia: a tabela verdade é totalmente verdadeira (V).
Contradição: a tabela verdade é totalmente falsa (F).
Contingência: a tabela verdade traz resultados V e F.
Por isso, resposta é a letra "b" (V e V).
Uma proposição composta formada por duas ou mais proposições p, q, r, ... será dita uma tautologia se ela for sempre verdadeira, independentemente dos valores lógicos das proposições p, q, r, ... que a compõem.
Contingência: verdadeiro ou falso.
Contradição: sempre falso.
GABARITO -> [B]
Questão de graça!
tao facil, que dá até medo kk
Tautologia: a tabela verdade é totalmente verdadeira (V).
Contradição: a tabela verdade é totalmente falsa (F).
Contingência: a tabela verdade traz resultados V e F.
Alternativa B
Tautologia: V V V V V V
Contradição: F F F F F
Contingência: V F V F V F
Tautologia: a tabela verdade é totalmente verdadeira (V).
Contradição: a tabela verdade é totalmente falsa (F).
Contingência: a tabela verdade traz, alternadamente, resultados V e F.
P V ~ P
V V F
F V F
O "V" (disjunção, OU) só é falso quando as duas forem falsas.
Tautologia é quando dá todos verdadeiros.
Gabarito: A
P v ~P será sempre um Taulogia.
P ^ ~P será sempre uma contradição.
Continue, continue... Não Desista!!!
Como a questão não pediu para "calcular" e sim para analisar a tabela, eu marcaria a questão B - Tautologia
Considerando a tabela-verdade apresentada, assinale a alternativa correta.
ele até facilitou já fazendo a tabela verdade, sendo assim é um tautologia, pois só deu V
CONTRADIÇÃO
P e ~P
TAUTOLOGIA
P ou ~p
CONTINGÊNCIA
São proposições cujo os resultados não são todos verdadeiro nem todos falsos.
Exemplo: Renato é vascaíno ou Marcos Antônio é flamenguista.
https://youtu.be/Aw_ztKtjl80 se vcs assistirem esse vídeo todo, a questão vai se tornar, extramamente, fácil. Nem acredito que entendi.
O que significa "implicação" na Lógica?
Seria o mesmo que implicação material/condicional/se... então/→
?????
Qual o erro da Letra D?
Lembro que para determinar se uma proposição é tautológica, contraditória e contingente a proposição precisa ser composta, ou seja, precisa de duas ou mais proposições simples, na questão traz apenas uma simples, mas é utilizada a mesma simples duas vezes para que seja valorada (P v ~P), nesse caso, mesmo que seja apenas uma simples, ela foi usada não de maneira isolada e sim para atribuir um valor lógico, se fosse apenas ~P, ai sim seria apenas uma simples, porque é apenas uma negação de uma proposição simples.
EXEMPLO CLASSICO DE TAUTOLOGIA.
P v ~P
V ou F = V
F ou V = V
Eu acertei, mas vi uma galera falando que não é pra calcular, só analisar a tabela, mas eu calculei e deu certo kkkk
Fiz assim:
p ¬ p
V F V
F V V
p v ¬p
V V V
F V V
Eu espelhei a tabela do P ~P e calculei usando o conectivo OU. Como o OU basta uma verdadeira pra ser verdadeiro, os resultados foram todos verdadeiro, ou seja, uma tautologia.
Eu não sei se fiz certo kkk
Em caso de erros, mandem msg :)
continue a nadar
Para a questão , foi adotada a seguinte notação: v significando disjunção; — significando conjunção; ¬ significando negação, V significando verdadeiro e F significando falso, “p” significando um exemplo de proposição e “q” significando um exemplo de proposição.
Considerando a tabela-verdade apresentada, assinale a alternativa correta
p ¬p ¬(¬p)
V F V
F V F
Letra C
As proposições p e ¬(¬p) são equivalentes, uma vez que os valores de p são iguais aos valores de ~(~p).
Achei que fosse tautologia, pois as duas são V: p e ~(~p)
tautológica, contingente e contraditórias são para proposições compostas, o que não é o caso da questão, trata-se de proposição simples na questão
Jean - São proposições SIMPLES P e ~P, ou seja, ~P não gera outra proposição apenas nega a primeira. Tautologia, Contradição e Contingência são para PROPOSIÇÕES COMPOSTAS! Tbm errei por falta de atenção. Espero ter sido clara.
Eu também errei com a malícia da questão.
Quando a questão coloca " p e ~(~p) " ela está falando da proposição simples p e da proposição simples ~(~p). Aqui, nós temos o conectivo "e" no sentido do português mesmo.
Então, temos que são equivalentes, pois se p for V, a negação de ~p também será V.
Se p for F, a negação de ~p também será F.
Se a questão tivesse colocado " p ^ ~(~p) " aí teríamos uma proposição composta, com o "e" no símbolo da lógica ( ^ ).
Diz-se que uma proposição P(p,q,r..) é logicamente equivalente ou equivalente a uma proposição Q(p,r,s..) se as tabelas-verdade dessas duas proposições são IDÊNTICAS.
p ¬p ¬(¬p)
V F V
F V F
GABARITO -> [C]
A questão traz uma malícia, mas é só lembrarmos da troca de sinais de matemática.
- - = + (menos com menos= mais) ou seja, P é a mesma coisa que ~(~P).
Avante !
2 É PAR
3 É ÍMPAR
NÃO+NÃO = SIM
NÃO+NÃO+NÃO = NÃO
Melhor explicação a do Alexandre:
"Diz-se que uma proposição P(p,q,r..) é logicamente equivalente ou equivalente a uma proposição Q(p,r,s..) se as tabelas-verdade dessas duas proposições são IDÊNTICAS."
Não poderia ser a letra a), visto que dependendo do valor lógico assumido por "p" o resultado poderia ser V ou F?
Simples, nenhum momento pediu para calcular nada, somente olhar as tabelas e dizer que são identicas.
a questão é bem simlples 99% interpretação 1% conhecer as regras .
simples!!!
p e ~(~p) são equivalentes
Eu errei porque não tinha entendido o comando da questão.
Depois de analisar com mais atenção, a questão quer que compare a coluna do P com a coluna do ~ (~P). Ou seja, tem que ignorar a coluna (tabela verdade do ~P.
Assim, por apresentarem a mesma tabela verdade, com os elementos nas mesmas posições em uma e na outra, as proposições P e ~(~P) são equivalentes.
Para a questão , foi adotada a seguinte notação: v significando disjunção; — significando conjunção; ¬ significando negação, V significando verdadeiro e F significando falso, “p” significando um exemplo de proposição e “q” significando um exemplo de proposição.
-----
As alternativas não referem o "e" como uma conjunção, e sim em sentido comum. Se não, a conjunção seria representada pelo travessão, conforme o comando da questão.
Fiquei na duvida entre a A e a C, mas lembro que para determinar se uma proposição é tautológica, contraditória e contingente a proposição precisa ser composta, ou seja, precisa de duas ou mais proposições simples, na questão traz apenas uma simples, poderia ser utilizada a mesma simples duas vezes, ai sim seria uma composta, mas como usou de maneira isolada é simples.
Como diz o Circo Gomes: "Veja bem!" Para termos uma TAUTOLOGIA todas as premissas devem ser Verdade
Já a CONTIGENCIA deve ter uma Verdade e uma Falsa
E a CONTRADIÇÃO deve ser todas Falsas
TAUTOLOGIA: VV
CONTIGENCIA: VF
CONTRADIÇÃO: FF
E a equivalência é quando eu tenho um ou dois valores, do quais têm o mesmo conteúdo lógico, por exemplo:
EX.1: P-->Q = (~Q-->~P)
EX.2: P-->Q = (~P v Q)
EX.3: P v Q = (~P-->Q)
#DEUS_ABENÇOE!!!!
Não precisa nem fazer tabela-verdade
p ¬(¬p)
V = V
F = F
BASTAVA OLHAR A COMPOSIÇÃO DELAS E VER QUE AMBAS TEM A MESMA TABELA-VERDADE.
PORTANTO, SÃO EQUIVALENTES.
GABARITO C
TENDI NADA
Gabarito: C
negação de uma negação = afirmação. Logo, a proposição ~(~p) é equivalente à proposição p
galera é so reparar na tabela verdade as proposições p e ¬(¬p) possuem os mesmos valores, logo são equivalentes
eu pensei da forma matemática -(-x) = +x
Não consta a alternativa correta! A sequência seria VFVV.
CONECTIVO SE ENTAO a única proposição falsa seria V com F igual F. O restante fica verdadeiro na tabela.
Hugo Duarte a alternativa correta realmente é a letra "b" como já foi dissertado pelo o Wellington...
disjunção conjunção condicional
P Q P ∨ Q P∧Q [P∨Q]-->[P∧Q]
V V V V V
F V V F F
V F V F F
F F F F V
Concordo com Wellington Beltrão.
Resposta B) VFFV
Não consta a alternativa correta! A sequência seria VFVV.
CONECTIVO SE ENTAO a única proposição falsa seria V com F igual F. O restante fica verdadeiro na tabela.
letra "B" correta a tabela do maik, a tabela quem tem que construir somos nós...
disjunção conjunção condicional
P Q P ∨ Q P∧Q [P∨Q]-->[P∧Q]
V V V V V
F V V F F
V F V F F
F F F F V
tem que comparar a coluna PVQ e P∧Q, o que resulta na ultima coluna
Obs:
Tautologia: tabela verdade toda verdadeira
Contradição: tabela verdade toda falsa
Contingência: tabela verdade verdadeira e falsa
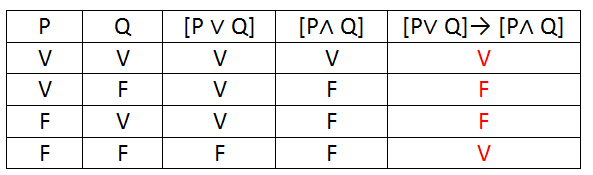
Para ajudar, existe um vídeo https://www.youtube.com/watch?v=tyLgDVuMt1I, muito didático, com dicas de memorização.
nossa que questão ingrata, toma muito tempo.
Nataxa Bobato, Essa questão não demorar mais que um minuto para fazer. Só saber que: Conjunção tudo V = V e na Disjunção tudo F=F e na Condicional V COM F = F
p^q V F F F
pvq V V V F
p->q V com F da F(só eh falso quando vai fugir)
Gabarito b. VFFV
Vou tentar responder da maneira mais facil
[ P v Q ] esse ( v ) virado para cima significa ( ou ) então aonde tiver V vai dar sempre V na tabela verdade : PRÓXIMO >>>>>>> [P∧Q] esse ( ∧ ) Virado para baixo significa ( E ) , quer dizer que so vai
P Q [ P v Q ] dar VERDADEIRA quando for V V = V o restante tudo F
V V = V P Q [P∧Q] V F = V V V = V
F V = V V F = F
F F = F F V = F
F F = F
SENDO ASSIM : [P∨Q]-->[P∧Q] , Agora que achou o resultado vai fazer o ( SE, ENTÃO ) ---> SO VAI DAR FALSO QUANDO TIVER V F = F O RESTO VERDADEIRO
[P∨Q] --> [P∧Q]
V V = V RESPOSTA LETRA ( B )
V F = F
V F = F
F F = V
Demorei uns 5min só pra entender a questão kkkkk, mas acertei letra B (:
Na tabela do Se...então... é só lembrar que a única proposição falsa é a: V - F = F >>> Vera Fisher é Fantástica. As demais são verdadeiras.
Obrigada pela explicação em vídeo, Prof. Chagas!
Errei de besteira, estava interpretando de outra maneiro e nunca iria acertar.
Se notarmos o resultado :V F F V é igual o resultado da ''bi condicional'' ,logo podemos dizer que: "os valores lógicos da ''condicional'' da (conjunção ===> disjunção) são mesmo valores da ''bi condicional''!!!!! VALE APENA APRECIAR DESSE MODO EM CASO DE FUTURAS QUESTÕES!
Se e então ----> V era F icher = F
Gratidão prof Ivan Chagas
Considerando que P e Q sejam proposições simples e que os
significados dos símbolos “P ∧ Q = P e Q", “P→Q = se P,
então Q" e “P↔Q = P se e somente se Q", a partir da tabela
abaixo, é possível construir a tabela-verdade da proposição
P↔Q.
P Q P→Q Q→P P↔Q
V V
V F
F V
F F
Dessa forma, assinale a alternativa que apresenta os elementos da coluna correspondente à proposição P↔Q, na ordem em que aparecem, de cima para baixo.
No bicondicional as proposições simples têm que ser iguais para a sentença ser verdadeira: V <-> V= V; F <-> F= V. Caso contrário a proposição será falsa.
d) VFFV
Em bicondicional, sera F se fro V<->F // F<->V. outra combinação sera V
Caraca, um rodeio desse para pedir uma coisa simples.
Qualquer dúvida sobre a tabela, acredito que será sanada com esse vídeo. Funcionou comigo.
https://youtu.be/Aw_ztKtjl80
estava montando errado, por isso a importância de resolver questões. separe o primeiro par que é v v e coloque um ao lado do outro como está aí, em seguida embaixo coloque o segundo par e assim sucessivamente de par em par. errei por colocar os primeiros 4 do lado dos últimos 4.espero ter ajudado
A QUESTÃO SÓ FALTOU CONTAR A HISTÓRIA DO BRASIL PARA DIZER QUEM É O ATUAL PRESIDENTE.
Marque C,se a proposição é verdadeira; E,se a proposição é falsa.
Dadas quais que proposições p e q,a proposição composta (p∧q) ∨(~ p ∧ ~q) é uma tautologia.
GABARITO ERRADO
Técnica do professor Josimar Padilha: "Quando a questão quiser uma Tautologia, que tem valor lógico (V), negue, tente provar que é falso.
(p ∧ q) ∨ (~ p ∧ ~q) = F
V ∧ F=F F ∧ V=F
--------- ------------
F ∨ F = F
Provei que é falso quaisquer que sejam os valores de p ou q.
MANTENHA-SE FIRME! BONS ESTUDOS.
isso é uma contradição...
resultado final dá tudo "F"
Resposta errada
É uma contingência VFFV
Confesso que não entendi muito bem a solução dos colegas. Consigo resolver assim:
(p ^ q) = V e V = Verdadeiro
V (ou)
(~p ^ ~q)= F e F = Falso
V ou F = Falso
Contigência (VFFV)
Montar tabela verdade:
_________________________________RESULTADO
P------ Q ~P----~Q (P^Q) (~P ^~Q) (P~Q)V(~P^~Q)
V-------V__F------F____V______F__________V
V-------F__F------V____F______F__________F
F-------V__V------F____F______F__________F
F-------F__V------V____F______V__________V
Para a tautologia ser verdadeira é necessário o resultado ser Verdadeiro. Seria verdadeiro se o resultado fosse V,V,V,V.
nas minhas contas deu contradição, f f
Marque C,se a proposição é verdadeira; E,se a proposição é falsa.
A proposição ~[(p ∨ ~q)∨ ~(p ∧q)]é uma contradição,quais quer que seja mas proposições peq.
CERTA
TAUTOLOGIA = todos os valores verdadeiros
CONTRADIÇÃO = todos os valores falsos
CONTINGÊNCIA = valores mistos.
Uma dica para além da tabeça da verdade: como são apenas duas proposições (P e Q) teremos 4 possibilidades:
P = V e Q=V
P=V e Q=F
P=F e Q=V e
ambas F.
Basta substituir e ver se TODAS as vezes dá falso (contradição). Se a questão pedisse tautologia, bastaria substituir e em todas as vezes teria que dar verdadeiro.
Este tipo de resposta vale também quando forem 3 proposições (P,Q,R), porém as opções seriam 9 (salvo engano meu) e daria mais trabalho, em tese. Em tese, porque as vezes na segunda ou terceira tentativa voce já que não é tautologia (a resposta dá FALSA) ou contradição (a reposta dá verdadeira).
Se p e q são proposições lógicas, então uma expressão lógica que é equivalente à expressão p → (~ q) é a expressão
Questão direta sobre equivalência lógica. Usando a representação geral P → Q ⇔ ~Q → ~P.
Portanto: p → (~ q) ⇔ q → (~ p)
p → (~ q) é equivalente a q → (~ p), pois estas proposições possuem a mesma tabela-verdade.
Dada uma proposição lógica p, é uma contradição a expressão lógica dada por
Gabarito: E
Uma contradição é uma composição de premissas nas quais todos os resultados dão falso.
p ^ (~p) equivale a dizer 'faço e não faço algo', que resultará sempre em conclusão falsa.
As outras alternativas:
a) Se a primeira premissa for falsa, teremos como resultado verdadeiro, independente da condição da segunda (condicional).
b) Idem ao a.
c) Em bicondicional, quando duas premissas possuem condições iguais (ambas verdadeiras ou ambas falsas), a conclusão será verdadeira.
d) O (~p) pode assumir valor verdadeiro, o que invalidaria a contradição.
Contingencia - F ou V
Contradição - F
Tautolofia - V
^ : e
~: negacao
p ^ (~p), significa que estou afirmando p e, depois, negando p. Ora, se afirmo algo e logo em seguido nego, estou me CONTRADIZENDO (p e não-p)
ALTERNATIVA E)
Considere a afirmativa “Todo gerente de projeto é programador".
Considere os predicados G(x) e P(x), que representam, respectivamente, que x é gerente de projeto e que x é programador.
Uma representação coerente da afirmativa acima em lógica de primeira ordem é
E) GENTE QUE CONFUSÃO CESGRANRIO. Eles querem medir a visão do candidato? Volta negando.
Representar G(x) → P(x) é o mesmo que dizer “Todo gerente de projeto é programador".
Contudo não há nas alternativas essa representação lógica, é necessário, portanto, achar a sua equivalência lógica.
G(x) → P(x) ⇔ ¬P(x) → ¬G(x). Portanto, letra "e".
Esse assunto é complicado de entender, mas essa proposição é elementar.
• Considere que (x) representa uma "pessoa".
• Considere que G é "gerente de projeto".
• Considere que P é "programador".
Logo, trocando por miúdos, a sentença implica em: "Se essa pessoa (x) for gerente de projeto (G), então (-->) ela será programadora (P)".
Como não há nas alternativas uma que represente diretamente a inferência, você precisa lembrar das regras de negação, da equivalência lógica dessa proposição: "nega-se tudo e inverte-se tudo, mantendo o conectivo.
G(x) --> P(x) = - P(x) --> - G(x)
Um provérbio chinês diz que:
P1: Se o seu problema não tem solução, então não é preciso se preocupar com ele, pois nada que você fizer o resolverá.
P2: Se o seu problema tem solução, então não é preciso se preocupar com ele, pois ele logo se resolverá.
O número de linhas da tabela verdade correspondente à proposição P2 do texto apresentado é igual a
Ainda não entendi!!
Se são 3 proposições na frase P2. Então qual é outro conectivo (além da Condicional é claro)?
São dois condicionais, Rodrigo. "Pois" retorna a causa de uma consequência anterior no texto. Algo como P -> (Q -> R)
O número de linhas da tabela-verdade de uma proposição composta qualquer é encontrado a partir da fórmula 2n, onde ‘n’ representa o número de proposições simples que existem nessa sentença.
Como a proposição composta P é formada por três proposições simples, então ela possui 8 linhas. Veja:
2n = 23 = 8
Assim, o item correto é a letra B.
Sou professor de Matemática e RLM e posto vídeos todos os dias em meu instagram com dicas e bizus dessas disciplinas. Quem quiser conferir, segue lá:
Instagram: @profjuliocesarsantos
Tenho essas e outras questões resolvidas em vídeo. Acesse http://www.tutorraciociniologico.com.br/
A fórmula para saber a quantidade de linhas de uma tabela-verdade é:
2 elevado a N
*sendo N: o número de preposições simples
Na questão: 2³= 8
Pois é sinônimo do conectivo Se...,então
"Se o seu problema tem solução, então não é preciso se preocupar com ele, pois ele logo se resolverá."
P->(Q->R)
Se o seu problema tem solução, ele logo se resolverá pois não é preciso se preocupar com ele.
Mas ainda acho que cabe recurso, porque sentença aberta não é proposição.
"Ele logo se resolverá".
Gab B
São três proposições dentro de 1 premissa.
2³ = 8
Pelas explicações eu entendi o seguinte:
Há uma condicional dentro de outra.
Proposições:
A: o seu problema tem solução
B: não é preciso se preocupar com o seu problema
C: o seu problema logo se resolverá.
O problema é como organizar isso em uma estrutura. Como a proposição B está deslocada no período, ela pode ir para o final do período. As palavras "pois" e "então" significam mesma coisa (consequência). Portanto podemos usar só a palavra então:
A -> (C -> B) = Se o seu problema tem solução, então o seu problema logo se resolverá. Se o seu problema logo se resolverá, então não é preciso se preocupar com o seu problema.
A proposição C é condição necessária para A e, ao mesmo tempo, condição suficiente para B.
Por fim,
O número de valorações possíveis é 2 (verdadeiro, falso) e o número de proposições é 3 (A,B,C). Logo, o número total de linhas é 2^3 = 8.
Abraços.
Ednildo Santos
A terceira parte é uma informação, como as duas primeiras partes.
P2 É A PREPOSIÇÃO COMPOSTA.
Nela existem 3 informações:
1- "Se o seu problema tem solução"
2- "ele logo se resolverá"
3- "pois não é preciso se preocupar com ele"
Fórmula da Tabela Verdade : 2³ = 8
Espero ter ajudado.
Minha contribuição.
Número de linhas de uma tabela verdade = 2 elevado ao número de proposições.
Sendo assim: 2³ = 2 . 2 . 2 = 8
Abraço!!!
O QC! eu pago pra resolver questões "COMENTADAS" ok?.
GOTE-DF
Para achar o número de linhas é só usar a formula 2^n.
Multiplica O RESULTADO por 2, PARA cada proposição (Linha)
UMA Proposição (1 linha) 2x1 = 2
DUAS Proposições (2 linhas) 2x2 = 4
TRÊS Proposições (3 linhas) 2x3 = 8
QUATRO Proposições (4 linhas) 2x4 = 16
CINCO Proposições (5 linhas)2x5 = 32
NÃO DESISTA !!!!
Se o seu problema tem solução, então não é preciso se preocupar com ele, pois ele logo se resolverá.
2x2x2 = 8.
É possível distinguir as preposições conforme a quantidade de verbos.
Se tiver errado meu raciocínio, me avisem por mensagem. Obrigada!
O número de linhas da tabela-verdade de uma proposição composta qualquer, é encontrado a partir da fórmula 2n, onde ‘n’ representa o número de proposições simples que existem nessa sentença.
Como a proposição composta P é formada por três proposições simples, então ela possui 8 linhas.
2n= 23= 8
O "POIS" DA ÚLTIMA PROPOSIÇÃO É UM SINÔNIMO DO SE...ENTÃO.
LOGO, CONTA COMO UMA PROPOSIÇÃO.
São 3 proposições.
P2:
1: Se o seu problema tem solução
2: então não é preciso se preocupar com ele
3: pois ele logo se resolverá
Fórmula: 2^n, sendo n o número de proposições 2*2*2 = 8
Julgue o item que se segue , a respeito de estruturas lógicas.
A expressão “Uma revisão dos pisos salariais dos professores assegurará a revolução na educação básica a que a sociedade aspira, pois qualquer reforma para melhorar a qualidade do ensino deverá passar pela valorização do educador” pode ser representada pela sentença lógica P→Q, em que P e Q sejam proposições convenientemente escolhidas.
Questão : CERTA
“Uma revisão dos pisos salariais dos professores assegurará a revolução na educação básica a que a sociedade aspira, pois qualquer reforma para melhorar a qualidade do ensino deverá passar pela valorização do educador”
O Pois é uma condicional igual ao o Se...então.
E se na frase você tirar o "pois" e colocar o "se..então" a frase continua com o mesmo sentido. Vejam
“Se uma revisão dos pisos salariais dos professores assegurará a revolução na educação básica a que a sociedade aspira, então qualquer reforma para melhorar a qualidade do ensino deverá passar pela valorização do educador”
Por isso a frase pode ser representada pela sentença lógica P→Q.
Corrigam-me se estiver errada!
Força!!!
Será composta , mas temos que observar que tem que inverter para ser o SE..., Então como a colega mencionou - Se (antecedente) qualquer reforma para melhorar a qualidade do ensino deverá passar pela valorização do educador então (consequente)uma revisão dos pisos salarias dos professores assegurará a revolução na educação básica a que a sociedade aspira.
Pois= Se.então
POIS é o condicional invertido
CERTO
Conjunções que equivalem ao Se...então: pois, quando, porque, sempre que, logo, portanto, da mesma forma.
CERTO Se (antecedente) qualquer reforma para melhorar a qualidade do ensino deverá passar pela valorização do educador então (consequente) uma revisão dos pisos salarias dos professores assegurará a revolução na educação básica a que a sociedade aspira.
Fica ligado, se você vir o Pois e o Desde de que é condicional.
Sinônimos do SE... ENTÃO
Quando...,...
Como ...,... (no começo)
Sempre que...,...
Consequentemente
...Logo...
Pois/Porque
Vejam como as questões se repetem no CESPE:
A proposição “A escola não prepara com eficácia o jovem para a vida, pois o ensino profissionalizante não faz parte do currículo da grande maioria dos centros de ensino” estaria corretamente representada por P -> Q, em que P e Q fossem proposições lógicas convenientemente escolhidas. ( Certo )
--
Uma breve reflexão minha sobre a atividade docente:
“Uma revisão dos pisos salariais dos professores assegurará a revolução na educação básica a que a sociedade aspira, pois qualquer reforma para melhorar a qualidade do ensino deverá passar pela valorização do educador”
Frase linda, mas na época meus professores de escola pública não iam dar aula nem precisavam bater ponto. Depois que veio este controle de presença, a maior parte da classe do magistério reagiu negativamente por perderam os "adiantamentos" de horários ( jogar duas ou três turmas dentro de uma sala para sair mais cedo ) e não poderem mais estourar o limite de faltas permitidas. São poucos os professores que realmente estão ali para querer tocar o aluno e são esses poucos que realmente tenho orgulho de chamar de mestre. Sinceramente, se um professor fosse uma classe burguesa, faria como as atuais elites do Estado: colocar o dinheiro no bolso e ir embora.
Portanto, mesmo reconhecendo as dificuldades da carreira do magistério ( como em qualquer outra carreira tem suas dificuldades ), não vejo os professores sempre como vítimas.
"Cara, a briga de verdade é saber quem é que fica na sombra" - Meu querido professor de Filosofia do 1ª ano.
CONDICIONAL --->
Todo; Como; Se; Caso; Quando; A não ser que; Contanto que; Salvo se; Sem que; Dado que; Desde que; A menos que.
BICONDICIONAL <--->
Assim como
CONJUNÇÃO ^
Mas; Contudo.
(Peguei nas aulas do professor Jhony Zini)
Vanessa Santos, você está equivocada. Quando aparece esse "pois", invertemos as proposições para colocar na condicional.
Eu interpretei como se p e q fossem respectivamente as proposições citadas, dessa forma pensei que teria que inverter a ordem e acabei errando a questão. Pelo fato de se dizer convenientemente escolhidas, "P→Q" já está com a ordem invertida, então ? sendo "p" a segunda proposição e "q" a primeira?
Uma situação que aprendi com o Prof Lustosa, é "Tenta transformar para as nomenclaturas que conhecemos".
Eu achei bem compreensivo colocar se ... então, e ficou fácil de identificar.
SÓ BASTA SABER ISSO:
POIS = SE ENTÃO
GABARITO= CERTO
AVANTE
!!!!
Se qualquer reforma para melhorar a qualidade do ensino deve passar pela valorização do educador, então uma revisão dos pisos salariais dos professores assegura a revolução na educação básica a que a sociedade aspira.
Minha contribuição.
Método Telles
Alberto é advogado, pois Bruno não é arquiteto
= Se Bruno não é arquiteto, então Aberto é advogado.
Abraço!!!
CONDICIONAL: -->
DECORE ESTA SEQUÊNCIA.
"SEMPRE QUANDO COMO POIS..."
CONDICIONAL: -->
DECORE ESTA SEQUÊNCIA.
"SEMPRE QUANDO COMO POIS..."
Lembrem-se que o que vem antes do "pois" é o consequente!
NA VERDADE a consequência vem ates do" pois". Logo seria SE qualquer reforma para melhorar a qualidade do ensino deverá passar pela valorização do educador ENTÃO uma revisão dos pisos salariais dos professores assegurará a revolução na educação básica a que a sociedade aspira
lembrando que ´pois, porquanto, porque, sempre que, logo, portanto= POR CAUSA" são conjunções que indicam uma CAUSA
pode ser representada pela sentença lógica P→Q, em que P e Q sejam proposições convenientemente escolhidas. Exato posso jogar P como uma setença JÁ INVERTIDA!
certo
pois = se
Questão
Uma revisão dos pisos salariais dos professores assegurará a revolução na educação básica a que a sociedade aspira, pois qualquer reforma para melhorar a qualidade do ensino deverá passar pela valorização do educador” pode ser representada pela sentença lógica P→Q, em que P e Q sejam proposições convenientemente escolhidas.
BIZU:
Se qualquer reforma para melhorar a qualidade do ensino deverá passar pela valorização do educado, então uma revisão dos pisos salariais dos professores assegurará a revolução na educação básica a que a sociedade aspira.
Gabarito correto. ✅
Julgue o item que se segue , a respeito de estruturas lógicas.
A proposição “A estabilidade econômica é dever do Estado e consequência do controle rígido da inflação” pode ser representada pela sentença lógica P→Q, em que P e Q sejam proposições simples convenientemente escolhidas.
“A estabilidade econômica é dever do Estado ^ A estabilidade econômica é consequência do controle rígido da inflação”
P ^ Q
Esta é uma proposição simples.
É uma proposição simple. O "e" não é cnectivo lógico.
Só tem um verbo.
ATENÇÃO COM A PALAVRA CONSEQUÊNCIA!
Quando a palavra consequência aparecer na frase observe se há uma relação de causa/efeito e se houver será proposição composta. Além disso, se há entre a palavra "consequência" dois verbos (de preferência no infinitivo) será uma proposição composta, se não houver, é simples.
Ex.: Passar (v. no infinitivo) é uma consequência de estudar (v. no infinitivo) = prop. composta
Ex.: A educação é (apenas um verbo) uma consequência de um país sério = prop. simples
A estabilidade econômica é (um verbo) dever do Estado e consequência (não há verbo após a palavra consequência) do controle rígido da inflação = proposição SIMPLES.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Em casos como esse se deve observar se há verbo no INFINITIVO antes e depois do termo "e consequência", não havendo, não há proprosição composta.
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
“A estabilidade econômica é dever do Estado e consequência do controle rígido da inflação” pode ser representada pela sentença lógica P→Q, em que P e Q sejam proposições simples convenientemente escolhidas. Errado!!! Não é proposição, pois exprime ordem. CUIDADO com a palavra DEVER
ERRADO
Olha só caindo em 2018
Ano: 2018 Banca: CESPE Órgão: ABIN Prova: Oficial Técnico de Inteligência - Conhecimentos Gerais
Julgue o item a seguir, a respeito de lógica proposicional.
A proposição “A vigilância dos cidadãos exercida pelo Estado é consequência da radicalização da sociedade civil em suas posições políticas.” pode ser corretamente representada pela expressão lógica P→Q, em que P e Q são proposições simples escolhidas adequadamente.
ERRADO
“A estabilidade econômica é dever do Estado e consequência do controle rígido da inflação”
TEMOS UM VERBO E O CONECTIVO "E". TEREMOS UMA PROPOSIÇÃO SIMPLES. O "E" NÃO IMPLICA NA EXISTÊNCIA DE OUTRO VERBO IMPLÍCITO.
MUITOS PODEM LER DA SEGUINTE FORMA:
“A estabilidade econômica é dever do Estado e É consequência do controle rígido da inflação”
OCORRE QUE NÃO HÁ VERBO IMPLÍCITO QUANDO TEMOS UM SUPOSTO CONECTIVO "E".
ATENÇÃO:
CASO FOSSE:
“A estabilidade econômica é dever do Estado OU consequência do controle rígido da inflação”
TERÍAMOS UMA PROPOSIÇÃO COMPOSTA.
O VERBO APÓS O "OU" ESTARIA IMPLÍCITO.
"COMO VOCÊ SABE DISSO?", VOCÊS PERGUNTAM.
EU RESPONDO: RESPONDENDO AS QUESTÕES.
RESUMO:
1 VERBO + E(^) = SIMPLES
1 VERBO + OU (V) = COMPOSTA.
vocês são @chatos . comentários enormes.... sejam objetivos !
a questão e considerada como preposição simples então não tem como ser representada por P→Q,
Errada ---> Esse condicional não existe.
Todas as questões que respondi até hj da banca CEBRASPE nunca o É consequência configurou uma condicional.
❌Gabarito Errado.
Veja que na primeira parte tem verbo, sentido, então é proposição: A estabilidade econômica é dever do Estado.
Na segunda parte depois da palavra consequência não existe verbo então não tem como ser uma segunda proposição mas sim continuação da primeira: A estabilidade econômica é consequência do controle rígido da inflação”
Então chegando em uma conclusão é uma única proposição, ou seja, é simples.
Bons estudos!✌
A proposição “A estabilidade econômica é dever do Estado e consequência do controle rígido da inflação” pode ser representada pela sentença lógica P→Q, em que P e Q sejam proposições simples convenientemente escolhidas.
A proposição “A estabilidade econômica é dever do Estado e consequência do controle rígido da inflação” pode ser representada pela sentença lógica P, em que P é uma proposição simples.
Proposição simples: Não pode ser quebrada em duas partes, sem que uma independe da outra para fazer sentido.
Separou as duas partes, uma parte faz sentido, e a outra não, é proposição simples.
Separou as duas, cada uma apresenta algum sentido, sem depender da outra parte, é proposição composta.
Agora vem o bizú: Você observou mais de um conectivo, separou as partes, e uma das partes ainda continua sem sentido completo, significa que eles são apenas conjunções, e não conectivos lógicos.
“O conectivo lógico te levará a uma sentença conclusiva, em cada parte separada”. Ex: Ana e Cláudia fizeram um bolo (esse “e”, é um “e” de adição, não permite separar os nomes e manter algum sentido isolado)
Outro exemplo: Ana e Cláudia fizeram um bolo e Marcos pudim. (a-Ana e Cláudia fizeram um bolo; b- Marcos fez um pudim). Na proposição, somente o segundo “e” é conectivo).
abs.
P Q R S
V V V
V V F
V F V
V F F
F V V
F V F
F F V
F F F
Com base na tabela apresentada acima, referente ao início da construção da tabela-verdade da proposição S, composta de P, Q e R, que são proposições lógicas simples, julgue o item a seguir.
Se S = Q↔(P ∨R), a coluna correspondente à proposição S, depois de preenchida a tabela-verdade, mostrará, de cima para baixo e nesta mesma ordem, os seguintes elementos: V, F, F, F, V, V, F, V.
Q: V V F F V V F F
P v Q: V V V V V F V V
S: V V F F V F F V
S = Q ↔️ (P v R)
1* teste : conectivo v
VV = V
VF = V
VV = V
VF = V
FV = V
FF= F
FV = V
FF = F
2* teste: conectivo ↔️
Q ↔️ resultado
VV =V
VV= V
FV = F
FV = F
VV = V
VF= F
FV = F
FF = V
GABARITO: ERRADO
SEQUENCIA: VVFFVFFV
errou ja na 2° linha: se p \/ r == V && q == V, logo (p\/q) <->q == V<->V == V
P Q R (P ∨R) Q↔(P ∨R)
V V V v v
V V F v v
V F V v f
V F F v f
F V V v v
F V F v f
F F V f f
F F F f v
Errado
PREFIRO QUESTOES DE TABELA VERDADE DESSA FORMA
É MAIS PRATICO E DINÃMICO
VVFFVFFV
O RUIM É O TEMPO QUE GASTA PARA FAZER.
Erro na segunda coluna.
Ordem correta: V V F F V F F V
No se somente se, só é verdade se forem iguais.
F <---> F = V
V <---> V = V
Minha contribuição.
P Q R... (Q).....(P v R)........... Q <-> (P v R)
V V V......V............V.....................V
V V F......V............V.....................V
V F V......F............V.....................F
V F F......F............V.....................F
F V V......V...........V.....................V
F V F......V...........F.....................F
F F V......F...........V.....................F
F F F......F...........F.....................V
Abraço!!!
Gabarito:Errado
Principais Regras:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação !!
seriam 16 linhas e não 8.
P Q R S
V V V
V V F
V F V
V F F
F V V
F V F
F F V
F F F
Com base na tabela apresentada acima, referente ao início da construção da tabela-verdade da proposição S, composta de P, Q e R, que são proposições lógicas simples, julgue o item a seguir.
Se S = (P→Q)∧(P→R), a coluna correspondente à proposição S, na tabela acima, conterá, de cima para baixo e na ordem em que aparecem, os seguintes elementos: V, F, F, F, V, V, V, V.
(P --> Q): V V F F V V V V
(P --> R): V F V F V V V V
S: V F F F V V V V
Resposta Certa. Construir a tabela-verdade e correr pro abraço.
quadrado é considero como se então?
O quadrado é Se então ---->
Correta.
P Q R P--->Q P--->R (P--->Q) ^ (P--->R)
V V V V V V
V V F V F F
V F V F V F
V F F F F F
F V V V V V
F V F V V V
F F V V V V
F F F V V V
Terminando a tabela-verdade proposta no enunciado, temos:
Logo, de acordo com a coluna em vermelho, a resposta é: Certo
| P | Q | R | P --> Q | P --> R | (P-->Q) ^ (P-->R) |
| V | V | V | V | V | V |
| V | V | F | V | F | F |
| V | F | V | F | V | F |
| V | F | F | F | F | F |
| F | V | V | V | V | V |
| F | V | F | V | V | V |
| F | F | V | V | V | V |
| F | F | F | V | V | V |
Correta.
P Q R P--->Q P--->R (P--->Q) ^ (P--->R)
V V V V V V
V V F V F F
V F V F V F
V F F F F F
F V V V V V
F V F V V V
F F V V V V
F F F V V V
SDDS DE QUANDO VOCE ERA ASSIM CESPE SUA LINDA, VOLTA PRA NÓS!
Esses tipos de questões Tabela-Verdade não estão caindo mais em concursos. A Cespe já sabe que o concurseiro pós-moderno domina Tabela-Verdade. Hehehe!
Minha contribuição.
P Q R (P -> Q)(P -> R) (P -> Q) ^ (P -> R)
V V V......V............V.....................V
V V F......V............F.....................F
V F V......F............V.....................F
V F F......F............F.....................F
F V V......V...........V.....................V
F V F......V...........V.....................V
F F V......V...........V.....................V
F F F......V...........V.....................V
Abraço!!!
Gabarito:Certo
Principais Regras:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação !!
Acabou tabelas da verdade.. Infelizmente! Não sei como em concursos pequenos ainda não colocaram até física quântica!
Cespe já foi do bem.
Quando o governo e as leis vigentes são incapazes de administrar os conflitos existentes entre as classes dominantes e as chamadas forças populares, ou de impedir o aumento do espaço político dessas forças, as classes dominantes apelam para golpes de Estado.
Considere as seguintes proposições:
P: O governo é incapaz de administrar os conflitos existentes entre as classes dominantes e as forças populares.
Q: As leis vigentes são incapazes de administrar os conflitos existentes entre as classes dominantes e as chamadas forças populares.
R: O governo é incapaz de impedir o aumento do espaço político das forças populares.
S: As leis vigentes são incapazes de impedir o aumento do espaço político das forças populares.
T: As classes dominantes apelam para golpes de Estado.
O número de linhas da tabela-verdade correspondente à proposição
do texto inicial é igual a
Como são 5 proposições, logo 2^5=32
questão maldooosaaa!
vamos separar as orações, cada uma com seu verbo:
P) O governo é incapaz de administrar os conflitos existentes entre as classes dominantes e as chamadas forças populares.
Q) As leis vigentes são incapazes de administrar os conflitos existentes entre as classes dominantes e as chamadas forças populares.
R) O governo é incapaz de impedir o aumento do espaço politico das forças populares.
S) As leis vigentes são incapazes de impedir o aumento do espaço politico das forças populares.
T) As classes dominantes apelam para golpes de Estado.
***Como são 5 proposições, logo 2^5=32
Gab: b
Na maior parte das questões, Cespe adota sujeito composto como proposição simples. Sacanagem essa aí.
nessa a cespe considerou sujeito composto como proposição composta, o que geralmente é proposiçao simples
Essa questão é ridícula!!!!
Isso é fruto de uma total desconsideração com o estudante!!!
Essa questão não tá certa!!!
Não é assim que funciona...qualquer estudante de filosofia e raciocínio lógico matemático sabe que há apenas 3 proposições simples na composição dessa proposição composta.
Examinador que não conhece a própria matéria da qual elabora as questões...
Ai fica complicado!!!
Quem afirma que essa questão tem gabarito correto desconhece a matéria!!!
Questão fila da p***, ela pediu para analisarmos de acordo com a proposição mostrada, vejam o enunciado: "O número de linhas da tabela-verdade correspondente à proposição do texto inicial é igual a", em momento algum fez referência as proposições fragmentadas que usou na questão anterior.
Não consegui visualizar !
Também não consegui visualizar!!
Pessoal, achei essa questão da CESPE com sujeito composto, nessa ela considerou como preposição simples.
Q448529- Cespe 2013
Com relação às proposições lógicas, julgue o próximo item.
A frase “O perdão e a generosidade são provas de um coração amoroso” estará corretamente representada na forma P∧Q, em que P e Q sejam proposições lógicas convenientemente escolhidas.
Resposta: Errado.
A frase “O perdão e a generosidade são provas de um coração amoroso” não é uma conjunção, é apenas uma proposição simples, pois exerce um único raciocínio, expressa uma única ideia.
Administrar, impedir e apelar.
3 verbos apenas.
Eu vou voltar pra roça!!!!!!
Não consigo enxergar 5 proposições, que questão doida!!
clodoaldo pascoal e Duda rp ----- citaram o "tchan" da questão!
:)
uma questão dessas eu deixaria em branco. Gente, isso nao pode mais acontecer!!! Os professores dessa banca ficam mudando de entedimento a cada questão, prejudicando o estudante e afrontando os próprios estudiosos de Raciocínio Lógico !! PALHAÇADA!!! Já tá na hora de ter uma lei para concursos!!!
Calma galera, nessa questão nós temos três sujeitos (governo, leis e classes dominantes). Na primeira parte do enunciado, temos dois suj (governo e leis), cada um com duas proposições. E na segunda parte temos uma proposição simples, com apenas um sujeito (classes dominantes) e um verbo (apelam).
Com isso temos: Suj governo: AvB
Suj leis: CvD (é o mesmo texto, porém são proposições diferentes, pois os sujeitos são diferentes)
Suj classes sociais: proposiçao E
- Ao todo temos 5 proposições, que nos dão 32 linhas na tabela verdade.
"Portugues, a mãe das matérias". Abraços!
Gente, se a prova deu as 5 proposições já separadas como apontou o colega Clodoaldo e Qconcurso não colocou aqui, realmente fica difícil acertar, pois em outras questões realmente o CESPE considera sujeito composto como preposição simples.
Vou apontar isso para eles
Interpretação sempre! Na hora da questão esquece a pressa, leia pausadamente.
Quando o governo[1prep.] e as leis[2prep.] vigentes são incapazes de ADMINITSRAR os conflitos existentes entre as classes dominantes e as chamadas forças populares, oooooouuuu (esse mesmo governo[3prep] e as leis vigentes[4prep.]) são incapazes de IMPEDIR o aumento do espaço político dessas forças, as classes dominantes [5prep.] apelam para golpes de Estado.
5 PREPOSIÇÕES DE FATO.
O governo e as leis vigentes são incapazes de ADMINISTRAR, OU o governo e as leis vigentes são incapazes de IMPEDIR. (SÓ AQUI JÁ CONSTA 4 + 1 (as classes dominantes apelam para golpes de Estado) = 5^2 =32)
Paciência e fé!!
#força
Se levarmos em consideração as questões anteriores que estabelecem, excepcionalmente, 5 premissas, tudo bem. Contudo, se for pra considerar a regra geral, gabarito incorreto sem dúvida. Mais uma daquelas questões que só a banca Cespe sabe fazer.
Quando o governo(1) e as leis vigentes(2) são incapazes de administrar os conflitos existentes entre as classes dominantes e (os conflitos existentes entre) as chamadas forças populares(3), ou de impedir o aumento do espaço político dessas forças(4), as classes dominantes apelam para golpes de Estado(5)
A Larissa Freire esta certa. O CESPE colocou as 5 preposições separadas na prova. O QConcursos foi muito sacana ao modificar a questão .
Complementando o comentário da colega Larissa Freire, de 02 de Fevereiro de 2017, às 00h49...
O que ela afirma está correto. A questão na prova está em outra formatação que se diferencia deste modelo no Qconcursos. Quem quiser pode verificar no link (prova no site PCI) a seguir, questão número 34.
https://arquivo.pciconcursos.com.br/provas/18774007/7c559cb5c8be/conhec_basicos_nivel_medio.pdf
Bom estudo
O gabarito dessa questão é a letra A, ou então paro de estudar, já que só consegui identificar 3 proposições aí. Abraço! valeu! VOU EMBORA DO BRASIL, PORQUE ATÉ PRA SER HONESTO AQUI TÁ DIFÍCIL.
Errei a questão... mas analisando bem... bem mesmo... consegui encontrar as 5 proposições:
QUANDO o governo E as leis vigentes são incapazes de administrar os conflitos existentes entre as classes dominantes e as chamadas forças populares, OU de (governo E as leis vigentes) impedir o aumento do espaço político dessas forças, as classes dominantes apelam para golpes de Estado.
Ficaria assim:
(P ^ Q) v (R ^ S) -> T = 5 proposições
2n(5) = 2.2.2.2.2 = 32
Obs.: o n é expoente (potencia de 5). Não consegui colocar o expoente...srrsrs
Se estiver incorreto, corrijam-me.
Bons estudos!
Já fiz várias questões e NUNCA vi uma questão dessas.
Cada sujeito uma proposição? A invencionice dessa banca não tem limites.
A questão deu as 5 preposições vamos somar as 5 né, mesma coisa é se a questão dá uma tabela verdade toda desconexa da realidade você tem que usar a tabela que a questão deu e não a sua que criou
SE o governo E se as leis vigentes são incapazes de administrar os conflitos existentes entre as classes dominantes e as chamadas forças populares, OU se (governo E se as leis vigentes) impedem o aumento do espaço político dessas forças, então as classes dominantes apelam para golpes de Estado.
questão subjetiva , não há certezas...
SE o governo E se as leis vigentes são incapazes de administrar os conflitos existentes entre as classes dominantes e as chamadas forças populares, OU se (governo E se as leis vigentes) impedem o aumento do espaço político dessas forças, então as classes dominantes apelam para golpes de Estado.
questão subjetiva , não há certezas...
Não precisa procurar nada já estava tudo separada logo abaixo.
Bom, respondi assim:
Proposições: P; Q; R; S e T
Usei a formula para encontrar a quantidade de linhas, assim como pedo o enunciado : "O número de linhas da tabela-verdade correspondente à proposição do texto inicial é igual a:".
2 elevado ao número de proposições, neste caso, 5.
5
2 = 32 (2*2*2*2*2)
Portanto, gabarito letra B, 32 linhas.
Essa questão é muito simples.
Se estiver errada, avisem, por favor.
A questão é que não é sujeito composto galera. Vejam que há proposições separadas.
Questão sinistra pra nível médio essa aí... Fiquei mais perdido que bêbado procurando caminho de casa ..
Não estou entendo por que as pessoas estão fazendo tanto alarde nessa questão. Analisando as proposições P,Q,R,S,T verás que tem 5 proposições. E a fórmula que todo mundo sabe para achar o número de linhas é: 2 elevado a N. No caso: 2x2x2x2x2=32.
O sacada do cespe nessa questão pra gente errar é fazer o candidato contar as preposições da frase inicial e não as que ELA separou.
VENCEREMOS
O número de linhas da tabela verdade é 2 elevado a n.
n= é o total de proposições.
2 elevado a 5 = 2x2x2x2x2 = 32
O que confunde é a repetição
GOTE-DF
Para achar o número de linhas é só usar a formula 2^n.
Multiplica O RESULTADO por 2, PARA cada proposição (Linha)
UMA Proposição (1 linha) 2x1 = 2
DUAS Proposições (2 linhas) 2x2 = 4
TRÊS Proposições (3 linhas) 2x3 = 8
QUATRO Proposições (4 linhas) 2x4 = 16
CINCO Proposições (5 linhas)2x5 = 32
NÃO DESISTA!!!
Creio que muitos perderam essa questão pelo tamanho do texto.
A sacada do Cespe nessa questão foi pegar o preguiçoso que não lê todas as informações, é perfeitamente visível a separação das proposições dentro do enunciado.
São 5 letras: P Q R S T, ou seja 2x2x2x2x2=32
Basta somente contar quantas letras tem e multiplicar n=2*
Como são 5 letras, ficará, N= 2X2X2X2X2= 32
Essa nem o Cebraspe acertava kkk
LETRA B
2 ELEVADO A 5= 2.2.2.2.2= 32 LINHAS.
A vitória está reservada para aqueles que estão dispostos a pagar o preço.
Desafio seria se a banca não tivesse separado as proposições.
Considere que as proposições lógicas simples sejam representadas por letras maiúsculas P, Q, R etc. A partir de proposições dadas, podem-se construir novas proposições mediante o uso dos símbolos lógicos ∧ e ∨, que significam, respectivamente, “e” e “ou”, ou por meio do emprego dos símbolos lógicos → e ↔, chamados, respectivamente, de condicional e bicondicional.
A proposição “As fontes de energia fósseis estão, pouco a pouco, sendo substituídas por fontes de energia menos poluentes, como a energia elétrica, a eólica e a solar — as fontes de energia limpa” pode ser representada simbolicamente por
Aos não assinantes:
Letra D
É uma proposição simples.
Resolução Material Estratégia:
Note que não temos NENHUM conectivo lógico. Na verdade estamos diante de uma proposição simples (“P”), embora a frase seja longa. Alternativa D.
''As fontes de energia fósseis estão, pouco a pouco, sendo substituídas por fontes de energia menos poluentes, como a energia elétrica, a eólica e a solar — as fontes de energia limpa”
Encurtando a frase:
As fontes de energia fósseis estão sendo substituídas por fontes de energia limpa. É uma proposição simples.
ou... ''estão sendo substituídas por fontes como energia elétrica, eólica e a solar.'' continua proposição simples
gabarito: letra D
proposição simples (“P”) D. Idéia única!!
Levei um tempinho para perceber que era uma locução verbal por conta da interferência do “pouco a pouco”
“As fontes de energia fósseis estão, pouco a pouco, sendo substituídas por fontes de energia menos poluentes, como a energia elétrica, a eólica e a solar — as fontes de energia limpa”
Nem todo E significa conectivo de conjunção. É necessário apresentar outra ideia.
“As fontes de energia fósseis estão, pouco a pouco, sendo substituídas por fontes de energia menos poluentes, como a energia elétrica, a eólica e a solar — as fontes de energia limpa”
Aqui entra também o português. O travessão é a especificação de cada uma então reescrevendo:
“As fontes de energia fósseis estão sendo substituídas por fontes de energia limpa"
Sem conectivo = proposição simples
A questão é tão simples que faz a gente errar.
"As fontes de energia fósseis estão, pouco a pouco, sendo substituídas por fontes de energia menos poluentes, como a energia elétrica, a eólica e a solar — as fontes de energia limpa"
Podemos ler esta frase da seguinte maneira:
As fontes de energia fósseis estão, pouco a pouco a pouco, sendo substituídas por fontes de energia menos poluentes, como por exemplo a energia elétrica, a eólica e a solar, que são fontes de energia limpa
Não há conectivos (o e seria conectivo se houvesse um verbo depois dele, como não há, ele é apenas um termo aditivo)
Encheram de informações com o intuito de confundir e encontrar os candidatos que entendem o que realmente é uma proposição!
“As fontes de energia fósseis estão, pouco a pouco, sendo substituídas por fontes de energia menos poluentes, como a energia elétrica, a eólica e a solar — as fontes de energia limpa”
RESUMINDO:
Energias limpas(elétrica,eólica,solar) substituíram lentamente as fósseis.
Resolvi a questão analisando como Proposição simples = P já q ñ da para quebrar em mais de uma.
CERTA.
Considere que as proposições lógicas simples sejam representadas por letras maiúsculas P, Q, R etc. A partir de proposições dadas, podem-se construir novas proposições mediante o uso dos símbolos lógicos ∧ e ∨, que significam, respectivamente, “e” e “ou”, ou por meio do emprego dos símbolos lógicos → e ↔, chamados, respectivamente, de condicional e bicondicional.
A representação simbólica correta da proposição “O homem é semelhante à mulher assim como o rato é semelhante ao elefante” é
Aos não assinantes:
Letra A
Bicondicional. Mas não consegui enxergar isso, pra ser sincero.
A semelhança homem-mulher ocorre simultaneamente com a semelhança rato-elefante, ou nenhuma das duas ocorre. Isto é, temos uma BICONDICIONAL, que é apresentada na alternativa A.
ASSIM COMO = Bicondicional < - >
duas proposições, temos a bicondicional
p<=>q
Tem de observar o aparecimento do assim como, caracterizando a bicondicional <=> . Bons estudos
Também creio que "assim como" seja um conectivo semanticamente mais próximo da conjunção. Todavia, cabe-nos deixar o senso crítico de lado ao responder questões da Cespe.
Quando houver conjunção comparativa cespe a considera como "se e somente se" embora dê impressão que possa parecer uma "conjunção" em termos de RLM...
A representação simbólica correta da proposição “O homem é semelhante à mulher assim como o rato é semelhante ao elefante” é
Esse fiquei na dúvida, entre a e c. Entendi o assim como como um aditivo(e)! “O homem é semelhante à mulher e o rato é semelhante ao elefante
GABA LETRA A DE AMOR.
Então, questão interessante, feita para aqueles que estudam duas matérias que, fiquem pasmos, andam juntas: português e RL, pois, pelo menos para o Cespe conseguimos resolver utilizando as conjunções, mas essa questão também dá para resolver utilizando-se a interpretação, vejam bem:
"O homem é semelhante à mulher assim como o rato é semelhante ao elefante"
Transformemos a frase:
O homem é semelhante à mulher, se e somente se, o rato for semelhante ao elefante.
É uma questão cabulosa, mas com um pouco de RACIOCÍNIO dá pra resolver. Qualquer dúvida ou sugestão estou por aqui.
A bicondição SE, E SOMENTE SE pode ser substituida por ... É EQUIVALENTE ...
Assim, podemos escrever a frase da seguinte forma:
O homem ser semelhante a mulher É EQUIVALENTE ao rato ser semelhante ao elefante.
Em português, "assim como" é conjunção comparativa. Porém, não podemos misturar conceitos, a prova de que não funciona está aí.
só vejo sendo a opção 'A' se for ironia...
Minha contribuição.
RLM
Se e somente se / <-> / Bicondicional
“O homem é semelhante à mulher assim como o rato é semelhante ao elefante”
“O homem é semelhante à mulher se e somente se o rato é semelhante ao elefante”
Conclusão: O homem é diferente da mulher, visto que um rato é diferente de um elefante.
Abraço!!!
EITA não sabia dessa marquei a C kkkk
Vivendo e aprendendo. Ta anotado
Vacilo
ALTERNATIVA A)
Formas alternativas de se representar o condicional "se e somente se"
Ex.: p<->q: "Pedro vai ao parque assim como Maria vai ao cinema."
Ex.: p<->q: "Pedro vai ao parque se e só se Maria vai ao cinema."
Ex.: p<->q: "Se Pedro vai ao parque, então Maria vai ao cinema e se Maria vai ao cinema, então Pedro vai ao
parque."
Ex.: p<->q: "Pedro vai ao parque somente se Maria vai ao cinema e Maria vai ao cinema somente se Pedro vai
ao parque."
Fonte: Estratégia Concursos
O homem é semelhante à mulher assim como o rato é semelhante ao elefante.
Se o homem é semelhante á mulher, então o rato é semelhante ao elefante.[
Se o rato é semelhante ao elefante, o homem é semelhante à mulher.
Visualizei assim.
A tabela a seguir apresenta as três primeiras colunas da tabela-verdade de uma proposição S construída a partir das proposições P, Q e R.
P Q R
V V V
F V V
V F V
F F V
V V F
F V F
V F F
F F F
Com base na tabela, assinale a opção que apresenta a sequência correta dos elementos constituintes da coluna da tabela-verdade correspondente à proposição lógica S: R ↔ (P∧Q).
No enunciado diz P,Q,R,porém,na tabela verdade mostrada na questão,os valores P,Q,R não estão na mesma ordem e sim R,Q,P,justamente para cofundir o candidato.
(P ∧ Q) tem como valores : V F F F V F F F
R ↔ (P ∧ Q) tem como valores: V F F F F V V V
GAB: LETRA D
d)
p q r (p^q) r<->(p^q)
v v v v v
f v v f f
v f v f f
f f v f f
v v f f
f v f f v
v f f f v
f f f f v
em se somente se, é V se os 2 valores forem iguais.
e, AND (^) so sera V se ambos forem V
P Q R P^Q S S = PROPOSIÇÃO COMPOSTA R ↔ (P∧Q)
V V V V V ^ = CONJUNÇÃO, ONDE VALOR LÓGICO SERÁ VERDADE, SE AMBAS (P,Q) FOREM VERDADE.
F V V F F ↔ = BICONDICIONAL, ONDE VALOR LÓGICO SERÁ VERDADE, SE AMBAS (R, P^Q) TIVEREM O MESMO
V F V F F VALOR LÓGICO.
F F V F F
V V F V F
F V F F V
V F F F V
F F F F V RESPOSTA LETRA D
Obrigada pelas explicações! Sem querer confundir ninguém... Achei o enunciado confuso, uma vez que fala que a tabela dada representa as três primeiras COLUNAS, mas a resposta a organiza em LINHAS.
Se fossem dadas as 3 primeiras COLUNAS, como são 3 proposições simples e distintas, minha tabela teria 8 linhas e ficaria estruturada assim:
(1ª COLUNA) VVVFVVVF (2ªCOLUNA) VFFVVVFF (3ª COLUNA) VFVFFFFF
P Q R
V V V
V F F
V F V
F V F
V V F
V V F
V F F
F F F
Não consigo deduzir, a partir do enunciado, que os 3 primeiros valores são linhas, depois mais 3 linhas, etc. :-(
Resolvendo a terceira linha, já dá pra dá para achar a resposta.
CUIDADO com a ordem na tabela!
Se V somente se V
se F somente se F
DICA: comece pela linha 2,3,6,7 que os resultados são diferentes nas alternativas
A tabela a seguir apresenta as três primeiras colunas da tabela-verdade de uma proposição S construída a partir das proposições P, Q e R.
P Q R
V V V
F V V
V F V
F F V
V V F
F V F
V F F
F F F
Ainda com base na tabela, assinale a opção que apresenta a sequência correta dos elementos constituintes da coluna da tabela- verdade correspondente à proposição lógica S: (P → Q)∨(P → R).
Aos não assinantes:
Letra A
A princípio pode parecer trabalhosa, mas pense assim: a disjunção ( "v") só é Falsa se os dois argumentos forem falsos, logo, com F v F; para que as condicionais, que servem como argumento na questão, sejam também Falsas, é preciso o Antecedente ser Verdadeiro e o Consequente ser Falso, logo, V -> F; Observando a tabela verdade, dá pra ver que só a penúltima linha tem este caractere e dá pra "matar" logo a questão.
"Toeval bestaat niet" Nada é por acaso. Vamos nessa!
Não entendi. Alguém poderia detalhar essa questão?
Elaine a questão trata de uma preposição lógica S: (P → Q) ∨ (P → R) e que deve ser resolvida a partir da tabela que esta previamente montada.
As vezes os alunos não atentam para a tabela montada e acabam montando a sua própria tabela, mas em ordem diferente. Isso não seria problema se a questão pedisse tautologia, contradição e contingência - Mas, neste caso em que o resultado tem ordem definida... aí sim precisamos seguir a montagem da questão.
PQR P->Q P->R (P->Q) V (P->R)
VVV V V V
FVV V V V
VFV F V V
FFV V V V
VVF V F V
FVF V V V
VFF F F F
FFF V V V
Alternativa correta letra A
Espero ter ajudado!
Montei a tabela verdade , deu certo! Alternativa "A": V / V / V / V / V / V / F / V.
1º Resolva o que está entre parênteses
Tem que seguir a montagem da questão!
Regra do "se então" → : Só é FALSO se 1º for V e o 2º for F
Regra do "ou" v : Só é FALSO se ambas F
(P → Q) ∨ (P → R)
V | V |V V V | V |V
F | V |V V F | V |V
V | F |F V V | V |V
F | V |F V F | V |V
V | V |V V V| F |F
F | V |V V F | V |F
V | F |F F V | F |F
F | V |F V F | V |F
GABARITO: A
a)
para p->q (se p entao q), so é F quando for V->F
para (p->q) \/ (p->r) so sera F se ambos forem F.
dica: responder primeiro a 1º linha e a última linha, ver o resultado e ir eliminando.
P Q R (P → Q)∨(P → R)
V V V v ∨ v = v
F V V v ∨ v = v
V F V f ∨ v = v
F F V v ∨ v = v
V V F v ∨ f = v
F V F v ∨ v = v
V F F f ∨ f = f
F F F v ∨ v = v
Minha contribuição.
P Q R (P → Q)∨(P → R)
V V V-------- V v V = V
F V V--------- V v V = V
V F V--------- F v V = V
F F V--------- V v V = V
V V F--------- V v F = V
F V F--------- V v V = V
V F F--------- F v F = F
F F F--------- V v V = V
Abraço!!!
Gabarito:A
Principais Regras:
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação !!
Gabarito A
I) Você verifica qual a possibilidade de S ser Falso
(P → Q)∨(P → R) = F
Note que OU é falso quando ambos os lados são falsos.
(P → Q)∨(P → R) = F
___F_______F
II) Então agora você faz cada parênteses e cada um tem que dá Falso.
(P → Q) = F
Aqui é o caso de Vera Fisher
(P → Q) = F
V___ F
Como encontrei o valor de P, é só substituir no outro parênteses.
(P → R) = F
V
Aqui é o caso de Vera Fisher
(P → R) = F
V___ F
III) Mostrando os resultados encontrados em S
(P → Q)∨(P → R) = F
V___ F___ V ___F
Note que quando tiver P = V; Q = F e R = F é a única opção de S ser falso.
Porque OU só será falso se ambos os lados forem falsos.
Então por isso é o item é V / V / V / V / V / V / F / V
___ = é só espaço, então você pode ignorar
As proposições podem ser escritas por meio de linguagem simbólica. A seguir são dados os símbolos (conectivos) e seus respectivos significados:
símbolo significado
~ não
∨ ou
∧ e
→ implicação
↔ dupla implicação
Considere as duas proposições a seguir:
p: Luiz Antônio é comerciante
q: Leda é esteticista
A proposição composta ~(~p ∨ q), em linguagem corrente, é:
Gabarito letra A
Errei a questão por não entender de cara que ela pede a negação (~p ∨ q) simbolizada pelo (~) antes do parenteses.
1° passo: a proposição composta (~p ∨ q) é uma disjunção, simbolizado pela (V)
2° passo: A negação da disjunção é o seguinte:
1) Negaremos a primeira preposição, nesse caso P. Mas percebam que ela já está negativa ~P, então a sua negação é a afirmação dela.
Ex de ~P: Luiz Antônio não é comerciante. A sua negação será a afirmação que Luiz Antônio é comerciante
2) Negaremos a segunda proposição. nesse caso Q
Ex: Leda é esteticista. Sua negação será Leda não é esteticista.
3) Sempre que uma questão nos der uma proposição disjuntiva, a sua negação será uma preposição conjuntiva (trocar OU pelo E).
Nesse caso a negação de (~p ∨ q) será (P ∧ ~Q)
Que é justamente a letra A
Luiz Antônio é comerciante e Leda não é esteticista.
Com relação à fórmula ∀y(P(x) ∧ ∃x(P(y) ∨ Q(x))) da lógica dos predicados, onde x e y são variáveis e P e Q são predicados unários, pode-se afirmar que
A questão deveria ser anulada pois o "para todo" só é usado com "se então".
Seja I uma função de valoração na lógica proposicional e a fórmula α= (P→ Q), onde P e Q são símbolos proposicionais. É possível afirmar que
A questão diz: α= (P→ Q)
Sendo assim a letra E está correta, pois para que I(α)=F será necessário que P seja verdadeira e Q falsa.
(P→ Q) = V → F = F
Sendo assim:
I( (¬P ∨ Q) → (P ∨ Q) )
(F V F) → (F V F)
F → F = V
_____________
Gabarito letra E