-
O custo médio será dado por CT/Y.
Como r = 1 e w = 2, podemos encontrar o valor de K e L. Isto porque o orçamento total é de 4, mas a firma gasta 50% do seu capital com cada insumo. Assim, a firma gastará 2 com K e 2 com L.
Como r = 1, a firma usa duas quantidades de capital, K (pois r.K = 1.2 = 2). Como w = 2, a firma usa uma quantidade de trabalho, L (pois w.L = 2.1 = 2).
Assim, como K = 2 e L = 1, temos:
CT = r.K + w.L
CT = 1.2 + 2.1 = 4
e
Y = L^0,5K^0,5
Y = 1^0,5.2^0,5
Y = 1.2^0,5 = 2
Se Cme = CT/Y. Então:
Cme = 4/2^0,5
Portanto, já podemos perceber que Cme não será igual a 4.
https://www.direcaoconcursos.com.br/artigos/gabarit-extraoficial-economia-para-tcdf/
-
Fala pessoal! Professor Jetro Coutinho na área, para comentar esta questão sobre Teoria dos Custos.
O custo médio é dado por CT/Y. Então, precisamos encontrar o valor de CT e o de Y para conseguirmos calcular o custo médio.
A banca nos disse que o custo do capital (r) é igual a 1 e que o custo do trabalho (w) é igual a 2. Como r = 1 e w = 2, podemos encontrar o valor de K e L.
A função de produção é y = k0,5L0,5. Repare que a soma dos expoentes de K e L é igual a 1. Assim, a firma gastará 50% do seu capital com capital e 50% com trabalho. Isso porque 0,5/1 = 0,5 = 50%.
Assim, o orçamento total é de 4 (dado do enunciado), mas a firma gasta 50% do seu capital com cada insumo. Assim, do total de 4, a firma gastará 2 com K e 2 com L.Como r = 1, a firma usa duas quantidades de capital, K (pois r.K = 1.2 = 2). Como w = 2, a firma usa uma quantidade de trabalho, L (pois w.L = 2.1 = 2).
Assim, como K = 2 e L = 1, podemos substituir estes dados na fórmula de custo total. Teremos:
CT = r.K + w.L
CT = 1.2 + 2.1 = 4
e
Y = L0,5K0,5
Y = 10,5.20,5
Y = 1.20,5 = 20,5
Se Cme = CT/Y. Então:
Cme = 4/20,5
Portanto, já podemos perceber que Cme não será igual a 4.
Uma outra forma de resolver a questão é pelo método de Lagrange. Neste método, montaremos uma equação com três variáveis e derivaremos essa equação em relação a cada variável.
O método de Lagrange será formado assim:
G = wL + rK - u(K0,5L0,5 - Y)
Agora, vamos substituir os valores, sendo que w = 2 e r = 1.
G = 2L + rK - u(K0,5L0,5 - Y)
A partir daí, derivaremos três vezes: em relação a L (dG/dL), em relação a K (dG/dK) e em relação ao u (dG/du). Essas derivações nos permitirão achar a relação entre K e L. Depois disso, é só substituir essa relação na função de produção, para encontrar o valor de K ou de L.
O cálculo completo está na figura abaixo:
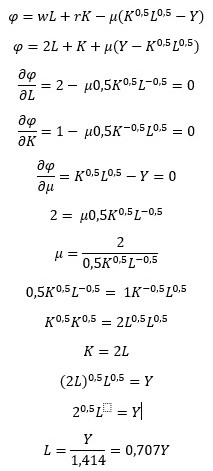
Assim, Y = 20,5.L
Para calcularmos o Cme, fazemos CT/Y
Assim: Cme = r.K + w.L/20,5.L
Cme = 2L + K/ 20,5.L
Como K = 2L (dado do Lagrange):
Cme = 2L + 2L/20,5.L
Cme = 4L/20,5.L
Cortando o "L" com o "L"
Cme = 4/20,5
Ou seja, repare que tanto pelo primeiro método quanto por Lagrange, chegamos ao mesmo resultado: Cme = 4/20,5
E já sabemos, então, que o Custo Médio não é igual a 4 o que torna o gabarito errado!
Surpreendentemente, a banca deu o gabarito como certo. Mesmo após os recursos, a banca manteve o gabarito como certo.
E aí, vem a surpresa. na justificativa para a manutenção do gabarito, a banca errou a conta. SIm, o Cespe errou a conta.
O examinador montou o método de Lagrange da seguinte forma:
G=4L+K+?(Y-K^0,5.L0,5)
Ou seja, o examinador considerou que o custo do trabalho é igual a 4 (w = 4). O negócio é que o próprio enunciado diz que w = 2.
Se você fizer w = 4, de fato, o Cme será igual a 4. Mas o dado do enunciado é que w = 2.
Não sei o que houve com o examinador nesta questão, mas, apesar do gabarito, a questão está mesmo errada.
Gabarito da Banca: CERTO.
Gabarito do Professor: ERRADO.
-
Não sou de reclamar de questões, mas a justificativa para a manutenção desse gabarito como "certo" é uma grande vergonha...... sinceramente viu Cebraspe.
O examinador usou o método de Lagrange para minimizar o custo, assim como o prof. Jetro demonstrou. PORÉM, o examinador utilizou w = 4 sendo que o enunciado fala explicitamente que w = 2
-
Justificativa cespe - claramente o examinador trocou o w=2 por w=4 e pelo jeito nem olham os pedidos de alteração de gabarito
Por construção teórica, no longo-prazo, os insumos capital e trabalho são variáveis.
Sendo assim, escrevendo-se o problema de minimização de custo da firma, tem-se: G=4L+K+?(Y-K^0,5 L^0,5 )
Condições de primeira ordem:?G/?L=4-?0,5K^0,5 L^(-0,5)=0?G/?K=1-?0,5K^(-0,5) L^0,5=0.
Resolvendo-se o problema acima, encontra-se: K=4l. Por sua vez: K=2yL=0,5y.
Sendo assim, a função custo total será tal que:
CT=wL+rK=4*0,5y+1*2y=4yO.
Custo total médio de longo-prazo será:
CTmédio=CT/y=4y/y=4.
O custo marginal é igual a derivada da função custo com respeito ao produto CMg=?CT/?y=4
-
Uma coisa que tem acontecido com frequência é o examinador adaptar questões de concursos anteriores. Perceba q provavelmente ele utilizou a questão da ABIN de 2018 (valor de w=4) para gerar essa do TCDF.
CEBRASPE (CESPE) - Oficial de Inteligência/Área 2/2018
A função produção de uma firma é descrita por Y = K1/2 L1/2, em que Y é produto, L é a quantidade de trabalho e K é o estoque de capital. Sabendo que, nessa firma, o salário é w = 4 e a remuneração do capital é r = 1, julgue o item seguinte.
- Se K = 2, então o custo total médio de longo prazo será igual a 2.