-
Agora vamos ver alguns exemplos um pouco mais complexos:
 |x - 5|
|x - 5|
Para obtermos o valor do |x - 5| precisamos identificar quando x - 5 ≤ 0 e quando x - 5 ≥ 0.
Ora, se x - 5 ≥ 0 então:
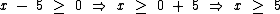
Logo para x ≥ 5 temos x - 5 ≥ 0, portanto segundo a definição do módulo temos:
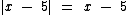
Já para x ≤ 5 temos x - 5 ≤ 0, de onde concluímos que:
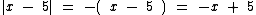
-
a) {x ? R | x ? 3}
Em funcao modular, fazemos o calculo 2x, 1 com -, e outra com +.
|x-2|::
(x-1)*(x-2)>=2
x²-3x>=2
Bascara::
x'= 2
x''= 1
|x+2|::
(x+1)*(x+2)>=2
x²+x-2>=0
Bascara::
x'= 3
x''=0
O unico valores deste quatro que obedece à inequacao é 3 porque substuindo x por 3 no modulus temos como resposta >=2.
-
É só pensar que qualquer valor dentro do módulo é +, então basta analisar o sinal da função x-1= 2
logo, x=3 então x>= a 3
-
x^logx = x. a formatação da questão engana, pois da pra assumir que o xlogx eh apenas x
-
Essa é a famosa questão que substituir é a melhor solução.
A
{x ∈ R | x ≥ 3} RESPOSTA
B
{x ∈ R | x ≤ 0 ou x ≥ 3}, se for numero negativo o f(X) vai ficar negativo porque lembre-se \x-2\ sempre vai dar positivo e o (x-1) dará negativo e positivo com negativo é negativo.
C
{x ∈ R | 1 ≤ x ≤ 2} o 1 e o 2 vão dar 0 e portanto menor que 2, logo também é falsa
D
{x ∈ R | x ≥ 2} o 1 e o 2 vão dar 0 e portanto menor que 2, logo também é falsa
E
{x ∈ R | x ≤ 1} se for numero negativo o f(X) vai ficar negativo porque lembre-se \x-2\ sempre vai dar positivo e o (x-1) dará negativo e positivo com negativo é negativo.