-
Período da manhã
48%.( 75) = 0,48.(75) = 36 mulheres
75 - 36 = 39 homens
Período da tarde
x = 3x + 36
7
7x = 3x + 252
4x = 252
x= 63
Do total de pessoas no período da tarde subtraio o número de mulheres que permanece o mesmo, tanto pela manhã quanto a tarde
63 - 36 = 27 homens
Homens pela manhã - Homens à tarde = 39 - 27 = 12 homens ausentes
-
Para melhor esclarecimento: _ na parte da tarde, a quantidade de homens é igual 3/7 do total de pessoas presentes naquele período e, não a quantidade de pessoas matriculadas. Por isso a necessidade de se calcular o X.
-
Total de funcionário: 75
Período da manhã:
48% mulheres = 36
52% homens = 39
Período da tarde:
3/7 do total de participantes são homens, logo 4/7 são mulheres que participaram em mesmo número do período da manhã.
como 4/7 = 36 e 36/4= 9 1/7 = 9 então 9x3 = 27 logo 3/7 = 27
reposta se dos 39 homens que deveriam estar presentes no período da tarde apenas 27 estavam, conclui-se que faltaram 12.
39 - 27 = 12
-
48% de 75=36 mulheres, logo 39 homens, se 3/7 são homens, logicamente 4/7 são mulheres. E se 4/7=36, eu posso dizer que cada 1/7 é 9. Prosseguindo, se 3/7 são homens e cada 1/7=9, 9x3=27. Daí é só pegar o total que é 39 e diminuir dos 27 que encontro 12.
-
Total: 75
75 * 0,48 = 36 (Mulheres)
7/7 - 3/7 = 4/7 (Mulheres) = 0,57
Logo
0,57 ---- 36
0,43 ----- x
x = 27
39 - 27 = 12
Muito Fácil
-
A questão não afirma que todos os homens estavam presentes no período da manhã, então eu não podeira calcular os 48% à partir de todos os 75 funcionários pois alguns dos homens poderiam ter participado apenas do turno da tarde.
Como não vejo como a questão poderia ser respondida sem considerar que todos os homens estavam presentes no período da manhã, considerei isso mas, acho que caberia anulação da questão.
-
Leia direito o enunciado, a questão fala que 75 funcionários participaram do seminário e desses, 48% eram mulheres...
Logo, da para entender que os outros 52% eram homens! O número só vai ser alterado no período da tarde.
A questão não colocou que o restante eram homens pq ja fica claro isso qdo diz a quantidade de mulheres presentes.
-
A base da porcentagem é 100
100% - 48% = 52%
Para encontrar a porcentagem aplique a fórmula: P = C * I / 100
Onde:
P = porcentagem
C = capital
I = taxa
P = C * I / 100
P = 75 * 52 / 100
P = 3900 / 100
P = 39
O total de homens é 39
O total de mulheres é 75 - 39 = 36
Quando o numerador é igual ao denominador temos uma fração aparente, ou seja ela representa o inteiro 7 / 7 = 1
7 / 7 - 3 / 7 = 4 / 7
As mulheres não faltaram.
36 mulheres corresponde a 4 / 7 do total que compareceram à tarde
Arme uma regra de três.
4 / 7 corresponde a 36
3 / 7 corresponderá a "x"
Para facilitar a operação aplique a técnica do cancelamento, Elimine 7 de 4 / 7 e 7 de 3 / 7, ficará:
4 corresponde a 36
3 corresponderá a "x"
3 * 36 / 4
108 / 4
27
À tarde compareceram 27 homens.
39 - 27 = 12
Faltaram 12 homens.
Resposta: 12 - letra e
Resolvendo pela regra de três:
100% corresponde a 75
48% corresponderá a "x"
48 * 75 / 100
3600 / 100
36
Total de mulheres 36
Total de homens 75 - 36 = 39
Quando o numerador é igual ao denominador temos uma fração aparente, ou seja, ela representa o inteiro 7 / 7 = 1
7 / 7 - 3 / 7 = 4 / 7
Como as mulheres não faltaram, 36 representa 4 / 7 do total que estavam reunidos à tarde.
O denominador de uma fração indica em quantas partes foram divididas o inteiro e o numerador quantas dessas partes foram consideradas.
Faça o inverso.
36 : 4 = 9, portanto, 1 / 7 corresponde a 9
Fração dos homens 3 / 7
9 * 3 = 27
Homens que faltaram:
39 - 27 = 12
Faltaram 12 homens.
Resposta: 12 - letra e
Ou resolva assim:
75 * 0,48 = 36
Total de mulheres: 36
Total de homens: 75 – 36 = 39
7 / 7 – 3 / 7 = 4 / 7
4 / 7 corresponde a 36, logo 1 / 7 = 36 / 4 = 9
Compareceram 3 / 7 dos homens, portanto, 9 * 3 = 27
Faltaram:
39 – 27 = 12
Resposta: faltaram 12 homens, letra e
-
De acordo
com o enunciado, tem-se:
total de
funcionários: 75
manhã:
48% do sexo
feminino: 0,48 x 75 = 36 mulheres
sexo
masculino: 75 – 36 = 39 homens
tarde:
total de funcionários
à tarde: t
homens:
3t/7
mulheres:
4t/7 = 36 mulheres
Assim,
4t = 7x36
4t = 252
t = 63
funcionários
homens:
3t/7 = (3 x 63)/7 = 27 homens
Finalmente,
a diferença é:
39 – 27 =
12 homens
Resposta E.
-
Período Manha: Feminino: 48% então 52% é masculino.
Período Tarde: Se masculino é 3/7 então feminino será 4/7
Considerando que Todas as mulheres participaram do início ao fim do seminário, teremos uma regra de três:
4/7 - 36
3/7 - X
4x/7 = (3*36)/7 - Simplifica o 7 ficando:
4x = 3*36 - Simplifica o 4 com o 36, para facilitar
x = 3*9 = 27 homens.
Logo o total de homens que faltaram a tarde será:
H = 39-27=12
Resposta E
-
75 (H e M)
48% de 75 = 36M
75 - 36 = 39H
3/7 -- H
4/7 -- 36
4/7H = 36 x 3/7
4H = 36 x 3
H = 9 x 3
H = 27
39H - 27H = 12H
-
Muito obrigada, Paulo Roberto achei seu comentário ótimo, mais fácil de aprender.
-
O enunciado ficou um pouco confuso ou me falta QI para melhor raciocinar.
Alguém além de mim pensou que o seminário teria sido dividido em duas turmas, uma pela manhã e outra à tarde? rs
-
Aqui, o total de funcionários é 75, e o percentual de mulheres no período da manhã era 48%. Portanto, a quantidade de mulheres (quantia de interesse) pode ser calculada lembrando que:
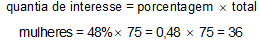
Se haviam 36 mulheres no total de 75 funcionários, o restante eram homens:
75 – 36 = 39 homens
Assim, pela manhã haviam 39 homens presentes, que representavam 52% (100% - 48%) do total de funcionários.
Com a saída de H homens à tarde, os homens passaram a ser 3/7 do total. Os homens que restaram eram 39 – H, e as mulheres que restaram eram 36. Assim:

Portanto, o número de homens que se ausentaram no período da tarde é H = 12.
Resposta: E
-
Mulheres: 75 x 0,48 = 36
Homens: 75 - 36 = 39
Manhã: 36 + 39
Tarde: 36 + (39 - H) ------> Total de participantes na ocasião.
A quantidade destes (39 - H) passou a ser igual a 3/7 do total de participantes na ocasião. Então temos:
(39 - H) = [36 + (39 + H)] x 3/7
7(39 - H) = 3[36 + (39 + H)]
273 - 7H = 3[75 +H]
7H - 3H = 273 - 225
4H = 48
H = 48/4
H = 12