SóProvas

ID
5383
Banca
CESGRANRIO
Órgão
Petrobras
Ano
2006
Provas
Disciplina
Raciocínio Lógico
Assuntos

Sabendo que cada anagrama da palavra PIRACICABA é uma ordenação das letras P,I,R,A,C,I,C,A,B,A, quantos são os anagramas da palavra PIRACICABA que não possuem duas letras A juntas?

Alternativas
Comentários

  • Todas as possibilidades de anagrama de PIRACICABA:
    10 letras com 2 I, 3 A e 2 C:

    P 10,(2,3,2) = 10!/(2!3!2!) = 151200

    Agora com as letras AAA juntas
    AAAPIRCICB
    Consideramos o bloco AAA como se fosse 1 só
    (AAA)PIRCICB
    P 8,(2,2)= 8!/(2!2!) = 10080

    O Bloco AA como se fosse 1 só
    (AA)APIRCICB
    P 9,(2,2) = 9!/(2!2!) = 90720

    Descontando do bloco AA o AAA
    Total: 151200 - 90720 + 10080 = 70560
  • olá, continuo sem entender.

    por que não descontamos apenas o bloco AA?

    digo desta forma:

    (AA)APIRCICB
    P 9,(2,2) = 9!/(2!2!) = 90720

    Total: 151200 - 90720

    thiagotrile@yahoo.com.br
  • .Possibilidades de anagrama de PIRACICABA:10 letras: 2 C, 2 I e 3 A.1° -> P 10,(2,2,3) = 10!/(2!2!3!) = 151200.Possibilidades com as duas vogais juntas (AA):2° -> 2!(AA)x 8! = 80640Resultado: 151200 - 80640 = 70560
  • Explicando o raciocínio da Louise.Possibilidades de anagrama de PIRACICABA: 10 letras: 2 C, 2 I e 3 A.1° -> P 10,(2,2,3) = 10!/(2!2!3!) = 151200Fatorial de 10 daria todas as possibilidades, mas divide-se pela multiplicação do fatorial das letras repetidas para excluir os anagramas idênticos, por exemplo:PiRACICABA == PIRACiCABA, invertendo-se as posições das letras I's, o mesmo anagrama será formado, desta forma ter-se-á dois grupos de anagramas idênticos, com as posições invertidas dos I's mas que representam os mesmos anagramas.2 letras I -> 2! -> Indica que serão 2 grupos de anagramas idênticos.2 letras C -> 2! -> Indica que serão 2 grupos de anagramas idênticos.3 letras A -> 3! -> Indica que serão 6 grupos de anagramas idênticos.Desta forma deve-se dividir o total do fatorial de 10 por 24 grupos de anagramas idênticos.-------------------------------------------------------------------------Possibilidades com as duas vogais juntas (AA):2° -> 2!(AA)x 8! = 80640Juntando-se duas letras A's, restão 8 letras para combinar e como as letras A's podem mudar de posição, por exemplo: AaPIRCBICA == aAPIRCBICA. Deste modo, serão 2 grupos repetidos de fatorial de 8.Resultado: 151200 - 80640 = 70560
  • O PH (EuVouPassar) explicou a questão de uma forma muito didática no YouTube. Acesse o link abaixo para assistir à explicação.

    http://www.youtube.com/watch?v=SwbOUJTx6as


    A explicação publicada diretamente no site dele pode ser vista a seguir.


    FALOU EM ANAGRAMA, FALOU EM PERMUTAÇÃO!

    Nesse caso, como tem letras repetidas, é permutação com repetição.

    Mas, o que é isso?

    Quando temos uma palavra com letras repetidas, e se fala em anagrama, precisamos calcular o total de anagramas (utilizando permutação), porém, por ter letras iguais, teremos anagramas repetidos. Assim, precisamos dividir o total de anagramas pela permutação da quantidade das letras repetidas.

    Na palavra PIRACICABA, as letras C, I (2 vezes) e A (3 vezes) estão repetidas. Então, para calcularmos o total de anagramas, temos:

    Anagrama = 10! (todas as letras de PIRACICABA) / 2! (letra C) . 2! (letra I) . 3! (letra A) = 151200

    Desse total, devemos retirar aqueles que tem duas letras A juntas. Façamos assim:

    Passa uma 'liga' nos dois A. Agora, teríamos 9 letras (contam os dois A como 1 só) = 9! / 2! (letra C) . 2! (letra I) = 90720



    Porém, dentro desse grupo, temos 3 A juntos. Teremos que tirá-los. 'Liga' nos 3 A = 8! / 2! (letra C) . 2! (letra I) = 10080

    Total = 151200 - 90720 + 10080 = 70560


    Resposta: Letra E.

    Fonte: http://beijonopapaienamamae.blogspot.com/2010/01/dia-02-de-janeiro-questao-02.html
  • Quem ficou na dúvida olhe o link do nosso amigo Vinicius.

    Abraços!!!
  • galera surgiu uma duvida: se eu tiro das combinacoes AA (2 A´s juntos) as combinacoes AAA (3 A´s juntos), isso quer dizer que a questao quer que exclua apenas com dois A´s juntos?? Então 3 A´s juntos não seríam excluídos?? Ao meu ver a questão deveria colocar "exclusivamente com dois A´s juntos".
    Passível de recurso.

  • Notemos que a palavra PIRACICABA possui 10 letras, mas com apenas 6 letras distintas, pois a  letra I ocorre 2 vezes, a letra A 3 vezes e a letra C 2 vezes, assim:

    Temos uma permutação com repetição,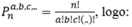 



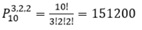
    Vamos agora considerar as 3 letras A’s como uma só:

                                                                          

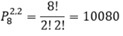
    E por último, consideremos as 2 letras A’s como uma  só:

                                                                          


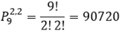
    Assim: 151200 + 90720 – 10080 = 70560

    Letra E.


  • O real motivo de retirar o grupo de três A's juntos (AAA) NÃO é porque a questão considerou que devem haver exclusivamente dois A's, mas sim porque é necessário eliminar repetições.

    Por exemplo, o anagrama AA87654321 e o anagrama 8AA7654321 podem gerar resultados idênticos, se a letra da posição 8 for um A.

    Para eliminar essa repetição, deve-se calcular quantas vezes ela ocorre. É uma repetição para cada vez que os três A's estão juntos, então temos que descontar os diversos anagramas com AAA.

    A conta fica melhor organizada assim:

    Número Total de Anagramas = 10!/(3!2!2!) = 151.200

    Grupo com dois A's juntos (com possível repetição do terceiro A) = 9.8!/(2!2!) = 90.720 --> como pode haver repetição, este número está exagerado!

    Anagramas com AAA = 8.7!/(2!2!) = 10.080 --> este valor será descontado do grupo acima para retirar as repetições.

    Portanto, o número total de anagramas sem dois A's unidos é:

    151.200 - (90.720 - 10.080) = 70.560