-
O texto do enunciado possui um erro de grafia e será corrigido em breve. Entretanto se olharmos na prova original:
(PVQ) ^ ~P -> (P^Q)v~Q
Tabela verdade de "Se, então" (->) só é falsa em: V -> F
Tabela verdade de "e" (^) será falsa se uma das variáveis também for falsa.
Tabela verdade de "ou" (v) será falsa somente quando as duas variáveis forem falsas.
Desta forma, se olharmos apenas para (P^Q)v~Q veremos que para ser falso dependerá diretamente de que Q seja VERDADE.
Resposta = ERRADO
-
A questão nos dá P: F
R = (PvQ)^(~P) --> (P^Q)v(~Q) ,
(PvQ)^(~P) --> (P^Q)v(~Q):F somente se (PvQ)^(~P):V e (PvQ)v(~Q):F
(PvQ)^(~P):V quando PvQ:V e somente quando Q:V essa preposição será verdadeira!
Se Q fosse falso, ficaria assim: (PvQ)^(~P) = (VvF)^V = V^V = V
Item errado
Boa Sorte!
-
Resolvi assim:
se o conectivo da primeira parte da proposição R é o "e", para que essa primeira parte seja VERDADE é preciso ser "verdade e verdade", se P tem valor lógico verdadeiro, o ~P tem que ser obrigatoriamente falso, o que torna falsa a primeira parte da proposição composta R.
se for falsa a primeira parte de uma proposição composta cujo conectivo é o "se... então", NUNCA ELA PODERÁ SER FALSA, será sempre verdadeira.
bons estudos a todos....
-
Amigos e colegas,
eu estou encontrando uma grande dificuldade de estudar lógica.
Alguém tem algum macete?
Não consigo inserir as alterações das afirmações nos exercícios.
Eu agradeço
bons estudos a todos
-
A quertão está errada!
Fiz assim:
R: ( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )
Se P é F e Q é V então R será F
( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )
FvV ^ V -> F^V v F
V ^ V -> F v F
V -> F
F
Se P é F e Q é F então R será V
( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )
F v F ^ V -> F^F v V
F ^ V -> F v V
F -> V
V
Conclui-se que vai depender do valor lógico de Q. Então R vai ser V ou F de acordo com o valor de Q. E não sempre Falso como afirma a questão.
Bons estudos a todos!!
-
R será sempre V.
-
Retificando o comentário do colega "alucard", nem sempre o valor será V, pois, como diz o enunciado, independente de Q ser V ou F, quando V, o resultado será F, contradizendo assim a generalização do prezado.
-
Usei a boa e velha tabela verdade:
| ~P | ~Q | P∨Q | P ∧ Q | ( P∨Q ) ∧ ( ~ P ) | ( P ∧ Q ) ∨ ( ~ Q ) | ( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q ) |
| F | F | V | V | F | V | V |
| F | V | V | F | F | V | V |
| V | F | V | F | V | F | F |
| V | V | F | F | F | V | V |
-
Colega Bruno Arcari,
Eu também tenho dificuldades em estudar lógica e o único "macete" que encontrei foi estudar muito esta matéria.
Fiz curso isolado, assisti todas as aulas do site euvoupassar (Prof. Tiago Pacífico) e resolvo muitas questões em pelo menos 1 dia da semana.
Força de vontade, determinação e fé em Deus chegaremos lá.
-
Fiz exatamente como a colega Michelle Canto.
Resolvi a questão com VALOR DE Q(FALSO) E Q(VERDADEIRO) preservando o P que foi dado como falso no enunciado da questão!
Fiz desta forma para economizar tempo, que é muito precioso nas nossas provas.
Admiro os colegas que conseguem inferir com segurança, apenas pelos conectivos. Ainda não cheguei neste nível.
-
Não sei se fiz certo, porém acertei a questão. Caso eu tenha feito errado, por favor me corrijam.
Só temos duas opções para o Q: V e F
opção 1: colocando o q com V e permanecendo o P como F, conforme o enunciado:(F v V) ^ V -> (F ^V) v F =
V ^V -> F v F=
V -> F= F ( na condicional a unica combinação que dá Falso é VF)
Opção 2: colocando o q com F e permanecendo o P como F, conforme o enunciado:
(F v F) ^V -> (F v F) v V=
F ^ V -> F v V=
F -> V= V ( na condicional quando a primeira for F, independente do valor lógico da segunda, a proposição será Verdadeira.)
Sendo assim, os resultados, nas duas opções são distintos, tornando a questão errada.
-
GABARITO: ERRADO
Senhores, não precisamos complicar o que se pode fazer de maneira simples, matei a questão com menos de um minuto sem sequer pegar a caneta! Leia...
Primeiramente, se você está com dificuldade nessa matéria, não tem mistério: DECORE a tabela-verdade. "Mas a matéria de lógica eu não preciso entender?" Sim e Não, pra essa parte da matéria, se você não tiver decorado a tabela, pode até achar respostas, mas vai levar um tempo que na hora da prova você não terá, portanto, DECORE:
http://1.bp.blogspot.com/_ivjE3SCM2dY/TC63urmmpdI/AAAAAAAAC0A/_bMuIccc0zg/s1600/Quest%C3%A3o+166-1.JPG
RESOLUÇÃO:
( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )
Diz a questão: P = "F", Q pode ser "V" ou "F", mas o resultado será sempre "F"
Observe que numa CONDICIONAL, se V → F = F mas se (independente de ser V ou F) → V = V será verdadeiro sempre
Portanto, basta que a "segunda parte" ( P ∧ Q ) ∨ ( ~ Q ) tenha a mera POSSIBILIDADE de ser VERDADEIRA
Conforme já estabelecido pela questão: P = "F"
Consideremos que Q pode ser "V" ou "F", podemos escolher. Vamos atribuir um valor "F": Q = "F"
( P ∧ Q ) v ( ~ Q )
( F ∧ F ) v ( ~ F )
F v V = V
Logo, temos que: (independente de ser V ou F) → V = V repare que o resultado, nesse caso, vai ser SEMPRE verdadeiro, contrariando a questão, que afirmou não haver essa possibilidade e, consequentemente, o item está errado.
Talvez pareça complicado, mas com o tempo a gente pega o jeito da coisa!
A dificuldade é para todos, fé, foco e persistência! Forte abraço
-
Analisando a questão,
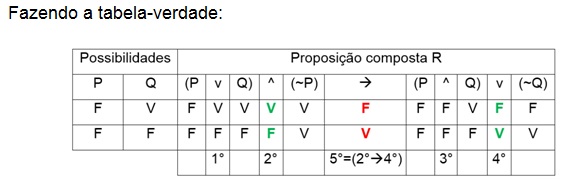
RESPOSTA: ERRADO
-
Senhores, sei que cada um tem uma maneira de estudar, contudo numa questão simples como esta utilizem a tabela verdade é o método mais seguro, meu resultado após a resolução deu VVFV, então nem sempre dará "F" como afirma a questão, como também nem sempre dará "V", pois temos uma contingência.
"Estude, pois a consequência lógica deste estudo será tua aprovação".
-
Sem tabela, só precisam ser feitos duas verificações para constatar o valor da conclusão. Sabe-se que o valor de P é falso, então:
1ª hipótese: Q (V):
[(PvQ) ^(¬P)]-->[(P^Q)v(¬Q)]
[(f v v)^(v)] -->[(f^v)v(f)]
[v^v] -->[fvf]
v--->f FALSA
2ª hipótese: Q (F)
[(PvQ) ^(¬P)]-->[(P^Q)v(¬Q)]
[(f v f)^(v)] -->[(f^f)v(f)]
[f^v] -->[fvf]
f--->v VERDADEIRA
Portanto, se o Q for Verdadeiro, R será falso. Gabarito ERRADO
-
( P v Q ) ^ ( ~P ) ----> ( P ^ Q ) v ( ~Q )
F V F
____________
F
Vou parar por aqui, já é o suficiente para resolver a questão, neste caso, independentemente de qualquer valor adicional,a preposição será verdadeira, pois na tabela verdade da condicional(----> ) só será F quando a primeira preposição for V e a segunda F.
-
Errado.
Simplifique, doí menos.:-P
Tá vendo o sinal da condicional? Pois é, sabemos que na condicional só é FALSO quando V ---> F.
Suponhamos que P: ( P∨Q ) ∧ ( ~ P )
e que Q: ( P ∧ Q ) ∨ ( ~ Q )
Logo, P-->Q = ?
F --> F= V ou F ---> V= V
-
Gabarito: ERRADO.
Isso mesmo, Juliana. Também pensei dessa forma.
Na condicional sabemos que só é FALSO quando a primeira proposição tem valor lógico verdadeiro e a segunda falso.
Então, se P é falso, independentemente do valor lógico de Q a proposição já pode ser considerada verdadeira, observem:
R= P ---> Q = F ---> V= V
R= P---> Q = F --->F= V
Qualquer coisa, ficarei grato se mandarem uma mensagem!
Bons estudos! Feliz ano novo!!
-
Atribuindo valor V para Q, temos:
(F v V) ^ (~F) → (F ^ V) v (~V)
V ^ V → F v F
V→F = F
Atribuindo valor F para Q, temos:
(F v F) ^ (~F) → (F ^ F) v (~F)
F ^ V → F v V
F→V = V
Gab: ERRADO
-
( P∨Q ) ∧ ( ~ P ) → ( P ∧ Q ) ∨ ( ~ Q )
Substituindo P=F
(FvQ)^(V)->(F^Q)v(~Q)
Retirando os elementos neutros...
Q->~Q
fazendo uma mini tabela
V F F
F V V
Gabarito: Errado
-
GAB. ERRADO
Se "Q" for FALSO, então "R" será VERDADEIRO.
TORNANDO A QUESTÃO ERRADA!
-
GAB E
O ou é o de boas, e só admite uma falsidade (F v F: F)
-
Errado, pois dependendo do valor lógico (V/F) atribuído ao '' Q '', a proposição R poderá ser verdadeira ou falsa.
-
Minha humilde contribuição. Conseguimos matar a questão,rapidamente, pegando apenas a 1a parte
a 2a parte vou chamar de = ?
(P v Q) ^ (~Q) -> (P^Q) v (~Q)
F v F ^ V
F ^ V
F
F-> ? = V
Logo, Gabarito E. A questão erra ao dizer independentemente.
O Q sendo F, R será Verdadeiro!!
Fé na Vitória!!!