-
casos possíveis: 420
casos favoráveis do 1o jovem:210
1o-caso possível/caso favoravel = 210/420= 1/2
casos possíveis: 420
casos favoráveis do 2o jovem:140
2o-caso possível/caso favorável = 140/420= 1/3
1o caso x 2o caso = 1/2 * 1/3 = 1/6
ou seja, nem é inferior nme superior, é igual a 1/6.
item errado
-
420 detentos ---> 210 roubo
----> 140 homicidio
----> +140 outros crimes
= 490
total de det. - 420
roubos/homicidios = 70
a questao pergunta:
a probabilidade de 2 detentos terem sido condenados por Rouvo (210) OU (+) Homicidio (140)
assim:
2 + 2 = 10 = 1
210 140 70 7
-
Iiii, calculei diferente, vejam se a minha linha de raciocinio esta correta.
Roubo 210
Homicidio 140
detentos 420
Probab roubo = 210/420 = 0,5 ou 50%
Probab homicidio =140/420 = 0.33 ou 33%
Prob. roubo x prob homici. = 0.5 x 0.33 = 0.165 ou 16,5%
sabemos q 1/6 = 0.166666 ou 16.6% Que é superior aos nossos 16.5%
dando como questao ERRADA.
ABRACO!!!
-
eu fiz: (1/2)*(1/2) + (1/3)*(1/3)
Não seria a probabilidade de ambos serem por roubo ou ambos por homicídio?
-
Nossa, cada um postou uma resposta diferente e eu também achei outra possibilidade. Antes disso: Gustavo, a sua fórmula não é possível , pois o resultado é de 13/36, o que deixaria a resposta certa.
Fiz assim:
Eu considerei apenas quem condenado por roubo ou homicídio , portanto eu excluí quem era condenado pelos dois em conjunto: 70 presos.
a) 210 condenado por roubo - 70 que cometeram os dois crimes = 140
140/420 = 1/3 . porém , preciso escolher dois dentre os 140 em um universo de 420. > 1/3 *1/3 = 1/9
B) 140 condenado por homicidio - 70 que cometeram os dosi crimes = 70
70/420 = 1/6 . porém , preciso escolher dois dentre os 70 em um universo de 420. > 1/6*1/6 = 1/36
Como a escolha era entre 2 condenados por roubo ou 2 condenados por homicído , temos de somar as probabilidades:
1/9 + 1/36 = 5/36 , que simprlificando é menor que 1/6 ( 6/36 )
Ou será que viajei !!
-
Na questão anterior calculamos que o número de presos por homicidio e roubo foi = 70.
Então subtraimos 210-70= 140 ( número de pessoas presas só por roubo)
Logo temos que dividindo 140/420= 1/3 ( probalidade de se achar apenas 1 pessoa no meio da multidão de presos)
Mesma conta faremos com os homicidas: 140-70 = 70
Portanto 70/420 = 1/6 ( probablidade de se achar 1 homicida na multidão)
Como a questão quer 2 presos então multiplicamos. 1/3*1/3 + 1/6*1/6 = 5/36 = 13,8%
Logo temos que é menor que 1/6 = 16,6%
-
vamos representar a distribuição dos presos, sabendo que alguns estavam presos por roubo e homicídio:
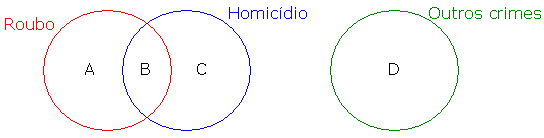
Sabemos ainda que:
O presídio continha 420 detentos
A + B + C + D = 420 (equação 1)
140 foram condenados por outros crimes
D = 140 (equação 2)
210 foram condenados por roubo
A + B = 210 (equação 3)
140 foram condenados por homicídio
B + C = 140 (equação 4)
Substituindo os valores de D e de A + B das equações 2 e 3 na equação 1, temos:
A + B + C + D = 420
210 + C + 140 = 420
C = 420 – 210 – 140
C = 70
Substituindo o valor de C na equação 4, temos:
B + C = 140
B + 70 = 140
B = 140 – 70
B = 70
Substituindo o valor de B na equação 3, temos:
A + B = 210
A + 70 = 210
A = 210 – 70
A = 140
Assim, temos:
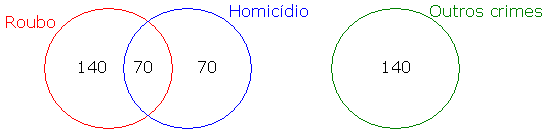
Fonte: http://raciociniologico.50webs.com/PCCE2012/PCCE2012.html#Questão 13
-
Utilizando o diagrama já construído anteriormente:

A interpretação do enunciado leva a resultados distintos. O que eu acredito que seja a intenção do Cespe é que os dois detentos devem ter sido condenados apenas por roubo, ou os dois detentos devem ter sido condenados apenas por homicídio. Aqueles detentos condenados por roubo e por homicídio não interessam nesse cálculo. Porém, acredito que cabe recurso, pois se escolhermos um detento condenado por roubo e homicídio e outro condenado por apenas por roubo, teremos escolhido dois detentos condenados por roubo.
Para os dois detentos condenados apenas por roubo:
P(1º apenas roubo) = (Casos Favoráveis)/(Casos Possíveis) = (140)/(420) = 2/6
P(2º apenas roubo) = (Casos Favoráveis)/(Casos Possíveis) = (140-1)/(420-1) = 139/419
Ptotal(apenas roubo) = P(1º) x P(2º) = (2/6) x (139/419) = (1/6) x (278/419)
Para os dois detentos condenados apenas por homicídio:
P(1º apenas homicídio) = (Casos Favoráveis)/(Casos Possíveis) = (70)/(420) = 1/6
P(2º apenas homicídio) = (Casos Favoráveis)/(Casos Possíveis) = (70-1)/(420-1) = 69/419
Ptotal(apenas homicídio) = P(1º) x P(2º) = (1/6) x (69/419)
Pfinal = Ptotal(apenas roubo) + Ptotal(apenas homicídio)
Pfinal = (1/6) x (278/419) + (1/6) x (69/419)
Pfinal = (1/6) x [(278/419) + (69/419)]
Pfinal = (1/6) x (347/419)
Como 347/419 é menor do que 1, podemos concluir que Pfinal é menor do que 1/6.
Item errado.Fonte: http://raciociniologico.50webs.com/PCCE2012/PCCE2012.html#Questão 13
-
Olha que simples.
210/420 + (ou) 140/420 = 1/6
-
Penso igual ao colega Gustavo Lima e acredito ser este o raciocínio correto. Se observarmos bem a questão, é dito 'condenado por roubo' somente. Não há qualquer ressalva sobre ser condenado APENAS por roubo ou homicídio. Assim, acredito ser este o raciocínio correto. Se a CESPE fez uma questão mal formulada ou interpretou errado o próprio texto, isso não é da conta dos examinados (pelo menos eu penso assim). Como o gabarito adotou a questão como ERRADA, acho totalmente passível de recurso.
algm sabe se foi anulada?
-
O raciocínio de Gustavo Lima está correto. Ainda que como ressaltou o wanderlei não concorde com o gabarito. Aqui não devemos torcer atropelando o enunciado até que se chege a resposta que a banca adimitiu.
Não se Lê em nenhum lugar ROUBO SOMENTE ou HOMICIDIO SOMENTE, portanto a resposta certa seria sim
(1\2)*(1\2)+(1\3)*(1\3)
Bons estudos
-
Concordo com os dois pontos de vista. Apesar de ter feito a questão como o Gustavo por ter compreendido que em nenhum momento ele fala SOMENTE ROUBO ou homicídio.
Realmente, esse tipo de questão é lamentável, o cara esquece de formular um enunciado correto e depois não quer anular para não perder dinheiro.
-
questão realmente mal formulada, mas atenção para a resolução do Digo, pois é exatamente assim que se resolve este tipo de questão. A forma simplificada como alguns resolveram deu certo aqui, mas pode não dar certo em outras. Quando se trabalha com dois eventos simultâneos deve-se desconsiderar o elemento sorteado no 1º evento para calcular o 2º. Apesar de a questão não informar se houve ou não reposição de elementos, enfim, mais uma questão estilo CESPE que faz uma bagunça em td aquilo q vc acredita q já aprendeu...
-
Pessoal, posso estar errado, mas seguindo o raciocínio que o Diogo postou, segundo link de resolução de outro site, concordo com o raciocínio, mas não com alguns resultados obtidos por lá.
A parte que calcula a interseção está correta, 70 é o número de detentos que foram presos por ambos os crimes.
Mas eu não concordo com o resultado do calculo da probabilidade de ambos para Roubo, abaixo meu calculo:
P1ºRoubo = 140/420 = 14/42 = 7/21 = 1/3
P2ºRoubo = 139/419 , aqui há um detalhe, essa fração é irredutível.
PAmbosRoubo = 1/3 * 139/419 = 139/1257 , que também é uma fração irredutível.
P1ºHomicidio = 70/420 = 7/42 = 1/6
P2ºHomicidio = 69/419 , outra fração irredutível.
PAmbosHomicidio = 1/6 * 69/419 = 69/2514 , outra fração irredutível.
Vamos chamar PAmbosRoubo de A e PAmbosHomicidio de B.
PA ou PB = 139/1257 + 69/2514 = 347/2514 , outra fração irredutível.
Na minha opinião, essa questão é NADA A VER, tanto a resolução como o resultado proposto por ela, mas é aquela história, se eu estiver errado, alguem me corrija por favor !!!
-
Esta questão deveria ter sido anulada por não colocar elementos suficientes, o problema é o seguinte:
para se calcular a probabilidade de um OU temos: P(A) + P(B) - (P(A e B))
Para simplificar, arredondando os cálculos temos:
P(A) Probabilidade dos dois serem condenados por roubo (e não SOMENTE por roubo)
210/420 * 210/420 (o correto seria 209/439 o que não tem relevância tendo em vista e mínima diferença)
que resulta em 1/2 * 1/2 = 1/4
P(B) Probabilidade dos dois serem condenados por homicídio (e não SOMENTE homicídio)
140/420 * 140/420 (mais uma vez o correto seria 139/419, diferença irrelevante)
que resulta em 1/3 * 1/3 = 1/9
P(A) E P(B) probabilidade de os dois serem condenados por roubo E homicídio
70/420 * 70/420 (irritantemente mais uma vez o correto seria 69/419)
que resulta em 1/6 * 1/6 = 1/36
Nesta situação teríamos 1/4 + 1/9 - 1/36 = (9 + 4 - 1)/36 = 12/36 = 1/3 logo resultado correto pois 1/3 > 1/6 (gabarito CERTO)
PORÉM para entender o resultado do gabarito há de se considerar
para P(A) e P(B), os SOMENTE por roubo e os SOMENTE por homicídio respectivamente
o que resultará ao final da bagunça 1/9 sendo portanto menor que 1/6 tornando a assertiva errada
da mesma forma a questão de conjuntos para se chegar a estas parciais "necessárias" também está errada pois poderia haver condenados por outros crimes e roubo OU por outros crimes e homicídio pois o próprio cespe já considerou tal situação, mas entendendo que não há condenados nessa situação as parciais são essas usadas na resolução.
obs: para os mais desconfiados e donos da razão acabei de assistir à resolução do prof Weber Campos desta questão, professor que está há anos ministrando aulas sobre questões do cespe
-
1º caso: Roubo e Roubo (210/420) * (209/420) = 1/4 Obs.: (209/420 = 1/2) valor irrelevante
2º caso: Homicídio e Homicídio (140/420) * (139/420) = 1/9 Obs.: (139/420 = 1/3) valor irrelevante
1º(roubo) ou 2º(homicídio) = 1/4 + 1/9 = 1/3
Correta (1/3 é maior que 1/6)
-
Questão ultra mal elaborada...
1. Probabilidade de que ambos tenham sido condenados por roubo:
210/420 * 209/419 ≅ 1/2 * 1/2 = 1/4
2. Probabilidade de que ambos tenham sido condenados por homicídio:
140/420 *139/419 ≅ 1/3 * 1/3 = 1/9
3. Probabilidade de que ambos tenham sido condenados por roubo OU (+) ambos por homicídio:
1/4 + 1/9 = 13/36 > 1/6
Como postado por diversos colegas, é lamentável que o CESPE não usa do Raciocínio para elaborar suas questões...
É óbvio para quem sabe o mínimo da matéria que quem foi condenado por Roubo E Homícidio entraria no cálculo de probabilidade dos dois eventos e não como alguns colegas, aceitando o resultado da banca, retiraram do cálculo a intersecção. Se algum examinador conseguir me provar que não é dessa forma, usando de Raciocínio Lógico, daí sim posso pensar em mudar de opinião.
Para quem tiver interesse, o raciocínio do examinador foi:
1. Probabilidade de que ambos tenham sido condenados por roubo (desconsidera a intersecção):
140/420 * 139/419 ≅ 1/3 * 1/3 = 1/9
2.Probabilidade de que ambos tenham sido condenados por homicídio (desconsidera a intersecção):
70/420 * 69/419 ≅ 1/6 * 1/6 = 1/36
3.Probabilidade de que ambos tenham sido condenados por roubo OU (+) ambos por homicídio:
1/9 + 1/36 = 4/36 + 1/36 = 5/36
Logo 5/36 < 1/6 (1/6 = 6/36)
-
Gente, uma dúvida:
"E" soma
"OU" multiplica
Ou seria o contrário?
;)
-
Olá Camylle;
É o contrário, ok?
E: Multiplica-se
OU: Soma-se
-
pessoal o espaço amostral é 420 correto, mas o numero de elementos não seria 280 entãi ficaria 280/420 que simplificando ficaria 2/3 para o primeiro preso.
aguém pode comentar?
-
EU PENSEI O SEGUINTE
APENAS POR ROUBO TEMOS 140/420=1/3
APENAS POR HOMICIDIO TEMOS 70/420= 1/6
ROUBO E HOMICIDIO TEMOS 70/420= 1/6
resolvendo por probabilidade temos
P(AUB)= P(A) + P(B) - p(AeB)
P(AUB)= 1/3 + 1/6 -1/6= 1/3 ( probabilidade de cada um)
AMBOS TEREMOS 1/3*1/3=1/9 QUE É MENOR QUE 1/6
-
R(210)+H(140)+O(140) = 490
Como só temos 420 detentos temos 70 detentos condenados por roubo e homicídio.
Observação:
e=*
ou=+
Logo:
R=210-70=140
H=140-70=70
R&H=70
O=140
Selecionando ao acaso 2 detentos a probabilidade de que ambos tenham sido condenados por roubo:
140/420*139/419 = 0,3333*0,3317=0,1105=11,06%
OU=+
Selecionando ao acaso 2 detentos a probabilidade de que ambos tenham sido condenados por homicídio:
70/420*69/419 = 0,1666*0,1646=0,2744=2,74%
0,1105+0,2744=0,1380=13,80% < 16,67% (1/6)
Resposta:ERRADA. A probabilidade será de 13,80%, inferior a 1/6 (16,67%)
-
roubo=140
homicidio=70
total de presos=420
probabilidade por roubo=140/420=1/3
probabilidade por homicidio=70/420=1/6
2por roubo+2por homicidio<1/6
1,3*1,3+1/6*1/6<1/6
1/9+1/36<1/6
logo falso
-
P= 140/420 x 139/419 = 1/3 x 139/419
P= 70/420 x 69/419 = 1/6 x 69/419
Soma das probabilidades : 1/3 ( 139/419 + 1/2 x 69/419) > 1/3 x 1/2
Gabarito E
-
tão simples explicar e o pessoal faz uma complicação!!!
TOTAL = 420
ROUBO = 210
HOMICÍDIO = 140
probabilidade de ocorrer roubo = (210/420) = 1/2
probabilidade de ocorrer homicídio = (140/420) = 1/3
se falar em "ou" = "soma"
se falar em "e" = "multiplica"
___________________________________________________________________
vamos a leitura:
probabilidade de ambos serem de roubo
1/2 "e" 1/2 = (1/2*1/2) = 1/4
___________________________________________________________________
probabilidade de ambos serem de homicídio
1/3 "e" 1/3 = (1/3*1/3) = 1/9
ou 1 ou outro ; ou roubo ou homicídio; ou 1/4 ou="+" 1/9
1/4 + 1/9 >>>>>>>>>>>>>>1/6
13/36 >>>>>>6/36
-
[(140.139)+(70.69)+(70.69)]/(420.419) = 0,1655 < 1,6666 ou 1/6
-
Sobre a polêmica de considerar ou não a interseção, em outra prova, o CESPE já considerou a interseção em questão muito parecida...
ver questão 26 em: http://www.cespe.unb.br/concursos/DPF_13_ADMINISTRATIVO/arquivos/DPF14_009_01.pdf
-
-
Selecionando-se ao acaso dois detentos desse presídio, a probabilidade de que ambos tenham sido condenados por roubo ou (então você soma) ambos por homicídio será superior a 1⁄6 .
1- 210 (roubo) + 140 (homicídios) = 350
2- Agora dividimos oq temos pelo que queremos (espaço amostral)
Probabilidade 1 Detento = 350/420 = 0,83
Probabilidade 2 Detento = 349/419 = 0,83
3- Por último SOMAMOS os resultados 0,83 + 0,83 = 1,66 que é diferente 1/6 (1/6 é 0,16)
-
Dentre todos os comentários, o do Alexandre, foi o melhor, e mais simples
contudo, o comentário da professora, está excelenteeee!!!!!!!!!
o QC deveria sempre pôr comentários de lógica em vídeo. Fica show.
-
Gostei do comentário de Pedro Muga.
A menos que eu esteja enganado por estar vindo duma fase muito cansativa de concurso e este é meu primeiro simulado sem está normal ainda:
Na minha opinião, deveria ser Probabilidade de Roubo + Probabilidade de Homicídio - Probabilidade de Interseção de Roubo+Homicídio. Vou representar assim: P(R) + P(H) - P(R ∩ H) Mas se vocês observarem, basta calcular P(R), pois as duas últimas se anulam porque são o mesmo número >>> P(H) - P(R ∩ H) = 0
Pode observar que Homicídio e "Roubo + Homicídio" são 70 detentos em cada grupo. Por isso se anula.
Então pra ganhar tempo na questão, bastaria resolver P(R).
Pessoal, deixem de criticar quem fez um comentário mais detalhado. Principalmente na área de exatas quanto mais comentário melhor, principalmente os mais detalhados para aqueles que estão começando ou que ficaram muito enganchados no problema. Até porque exatas tem uma linguagem não verbal e se for só uma única maneira de explicação fica inviável de entender na maioria das vezes.
-
Errata no comentário do colega Pedro Mugo, embora não altere o raciocínio da questão nem resposta final:
ele confundiu e digitou errado em
0,1666*0,1646=0,2744
Na verdade é 0,0274
Embora ele tenha escrito certo no formato % : 2,74%
-
Considera sim a interseção! Vi no comentário do professor.
-
GABARITO ERRADO
-questão lazarenta....contaiada boa de errar na hora da prova.
O pulo do gato é prestar a atenção no enunciado na parte que diz " Verificou-se, também, que alguns estavam presos por roubo e
homicídio " para não errar na hora de montar o diagrama de Venn.
N= 420
- roubo(210) + homicidio(140) + outros(140) = 490 - 420 = 70
roubo = 210 - 70 = 140
homicidio = 140- 70 = 70
outros = 140 (não subtrai pq o enunciado disse que apenas nos crimes de roubo e homicidio há detentos que cometeram ambos os crimes)
Calculo da probabilidade (quero/ tenho)
P de roubo = 140 / 420 => 1/3
P de homicidio = 70 / 420 => 1/6
- probabilidade de que ambos tenham sido condenados por roubo ou ambos por homicídio será :.
P de roubo = 1/3 x 1/3 => 1/9
P de homicidio = 1/6 x 1/6 => 1/36
(lembrando que na matemática E= multiplica ; OU = soma)
1/9 + 1/36 = 5/36
5/36 < 1/6
-
Total: 420
Condenados por roubo: 210
Condenados por homicídio: 140
Outros crimes: 140
420
l----------------------------------------------------------------------------------------------------l
l Roubo Homicídio l
l l----------------------l--------------l---------------------------------l l
l l 140 l 70 l 70 l l
l l----------------------l-------------l---------------------------------l l
l 140 (outros crimes) l
l-----------------------------------------------------------------------------------------------------l
P(selecionar dois e ambos sejam condenados por roubo OU selecionar dois e ambos condenados por homicídio) =
P(ambos só roubo OU ambos só homicídio OU ambos roubo E homicídio(interseção) ) =
140/420 * 139/419 + 70/420 * 69/419 + 70/420 * 69/419 =
0,333*0,333 + 0,1666 * 0,1666 + 0,1666 * 0,1666 =
0,11 + 0,028 + 0,028 = 0,166 = 1/6
É exatamente 1/6
ERRADO
-
Colega rebimboca da parafuseta está correto...
-
Faltou a palavra "somente" no enunciado da questão.
-
O número total de combinações de 2 dos 420 detentos é:

-
Passo 1
Pegue os 420 detentos e retire os 140, pois a questão quer saber a respeito dos crimes de Roubo e Homicídio. (420 - 140 = 280 (Esses praticaram apenas um ou ambos)
Passo 2: Somar 210 (Homicídios) + 140 (Roubo) = 350 (Está no enunciado)
Passo 3: 350 + 140 (Outros Crimes) = 490 ( Sabemos que 70 praticaram ambos os crimes, SÃO 420 DETENTOS, DIFERENÇA DE 70) Vamos ao Diagrama de Ven Galera:
Passo 4: Pegue os 210 e diminui 70 diferença do passo 3 ( Se faz necessário, pois dos 210, teremos o resultado de 140 presos que apenas roubou)
Passo 5: Pegue os 140 e diminui 70 diferença do passo 3 ( Se faz necessário, pois dos 140 que mataram, 70 teremos o resultado de presos que apenas praticou homicídio )
Resultado Final
140 Apenas Roubo
70 Apenas Homicídio
70 Ambos
140 Outros = 420
Pegue 420 e divide por 6= 70 Então o de roubo é sim superior a 1/6, pois encontramos o número 140, já os 70 por homicídio não é superior, são exatamente 1/6
Abs
-
Questão de certo e errado com mais erro que acerto, realmente é "muito" fácil igual professora falou no comentário no vídeo que ela fez. Fácil entender do enunciado que as 70 pessoas que cometeram mais de 1 crime, cometeram especificamente roubo e homicídio (e não roubo e outros, ou ainda homicídio e outros). Mais fácil ainda é adivinhar que quando a assertiva fala em "tenham sido condenados por roubo ou tenham sido condenados por homicídio", de fato a questão está querendo dizer "tenham sido condenados SOMENTE por roubo ou tenham sido condenados SOMENTE por homicídio", interpretação essa, que faz mudar o gabarito da questão. Realmente é mto fácil viu professora, é a gente que tem problema de aprendizado e não consegue fazer mesmo!! É cada uma q só por Deus!! (obs. se não quiserem perder tempo procurando um comentário mais completo, o único comentário realmente bom que vi até agora foi o do Murilo).
-
Pessoal, alguém poderia me explicar porque não se considera a interseção? Não consegui identificar no texto algo que indicasse que queriam somente ou outro
-
ERRADO, POIS É EXATAMENTE P= 1/6
Total: 420 presos
Roubo = 210
Homicídio = 140
Outros crimes = 140
interseção Roubo- Homicídio = 70
P = 70/420
SIMLIFICANDO ------ P= 7/42
P= 7/6x7
P= 1/6
-
se estiver com pressa... vai direto para o comentário do Rebimboca da parafuseta
Gratidão Senhor pelo presente.
-
Probabilidade de acertar sem saber a matéria = 50%
Probabilidade de acertar SABENDO a matéria = 0%
-
1 Probabilidade Roubo
140/420 x 139/419 = +- 1/9
2 Probabilidade Homicídio
70/420 x 69/419 = +- 1/36
------------------------------------------------
1/9 + 1/36 = 5/36
------------------------------------------------
5/36 < 6/36
GABARITO ERRADO
-
Resolução em vídeo:
https://www.youtube.com/watch?v=FstwrJw9q0E&ab_channel=HelderMonteiro
-
Transformem em fração e sejam felizes. 1/2 foi condenado por um crime e 1/3 por outro
-
O meu raciocínio foi o seguinte:
210/420 x 209/419 = 0,24
140/420 x 139/419 = 0,11
0,24 OU 0,11 = 0,24 + 0,11 = 0,35
0,35/2 = 0,17
0,35 eu dividi por 2, afinal é um ou outro.
1/6 (é o questão sugere) = 0,16
Se a questão diz que há detentos presos pelos dois crimes, logo no meu cálculo de 0,17 eles estão no meio. Mas eu não quero eles, então se eu tira-los, deixa de ser 0,17 e passa a ser menor que 0,16.
Gab: Errado
Espero que ajude!
-
Observem essa outra questão do cespe:
Caso se selecionem, ao acaso, duas pessoas, entre as 210 da amostra, a probabilidade de que ambas tenham procurado a unidade do DETRAN para solucionar pendências relacionadas à documentação de veículos ou que a tenham procurado para resolver problemas relacionados a multas será superior a 1/6.
Ela também utilizou o raciocínio de que se tratavam dos dos fatos separados. Esse é o entendimento da banca. Vamos anotar e seguir pra próxima.
-
57 DISLIKES NO VIDEO DA PROFESSORA, NÃO ENTENDI. A EXPLICAÇÃO DELA FOI PERFEITA.
-
140+140-70/420 = 210/420 = 0,5 -> 5/100 -> Simplifique tudo por 5 -> 1/20 menor que 1/6.
QUESTÃO ERRADA!
-
Resultado absurdo.
No enunciado o CESPE considera o fato de um condenado por roubo ser condenado por homicídio, e apenas cita "condenado por roubo". Porém na resolução, o CESPE exige que se tenha um entendimento diferente, ou seja, Considerar o crime isoladamente.
Lamentável...
-
1º - Temos 2 amostras. Xroubo e Xhomicidio.
2º - Separando corretamente temos que: R = 210; H = 140, O = 140. Sendo assim temos que : R = 70 (Apenas roubo 140 - 70 = 70), H = 140 (Apenas Homicídio 210 - 70 = 140), pois (210 - 140 = 70 (roubo e homicídio, interseção do evento A|B).
3º - P = N / TOTAL .
4º - 2 Agentes de roubo (apenas) ou homicídio (apenas).
5º- Roubo => P = 70 / 420 = 0.166... (Agente 1) X P = 69 / 419 = 0.164... (Agente 2).
P (1) . P (2) = 0.166 x 0.164 = 0.0272 (aproximadamente).
6º - Homicídio => P = 140 / 420 = 0.333... (Agente 1) X P = 139 / 419 = 0.331... (Agente 2).
P (1) . p (2) = 0.333 x 0.331 = 0.110 (aproximadamente).
7º - Quando falar no enunciado a palavra (OU = Soma) e quando falar (E = Mutiplicar) os resultados das probabilidades.
Sendo assim, ficará: P (Roubo) + P (Homicídio) = 0.0272 + 0.110 = 0.1372 (aproximadamente)
0.1372 x 100% = 13,72 < (1/6 = 0.166.. (16.6%))
-
Não sou de brigar com a banca, mas esse tipo de interpretação é um ilícito com o candidato. A Cebraspe vai contra sua própria doutrina interpretativa, incrível.....
-
O problema não é tanto saber fazer,mas o tempo que ira perder em um concurso.
-
primeiro, vc tem que descobrir quem é SÓ ROUBO e quem é SÓ HOMICÍDIO, pra depois fazer os cálculos, soluções apresentadas como simples e rápidas, embora acerte o gabarito, não são corretas. Muito cuidado, porque pode levar o ponto, mas talvez não terá tanta sorte em outras questões....e não estudamos para depender da sorte, não é?
A solução da Thamara Coutinho está correta.
-
210/420 + 140/419 (melhor arredondar para 140/420)= 1/2+1/3= 1/6, porém, como há a diferença do 420 para o 419, do arredondamento, deduz-se que será menor que 1/6. Formula pratica de fazer.