-
Sabendo-se que o conjunto X é dado por:
X = {x ∈ R ¦ x2 – 9 = 0 ou 2x – 1 = 9}
Temos o seguinte conjunto solução para o Conjunto X:
X2 - 9 = 0 --> x = - 3 ou x = 3 (estes são os valores que, ao atribuirmos a x, irão satisfazer a condição da expressão " X2 - 9 = 0" ), pois (-3)2 = 9 e (3)2 = 9 "OU " 2x - 1 = 9 --> o único valor que x poderá assumir para que a expressão seja válida é x =5 pois (2 * 5) -1 = 9 (obs: o sinal * denota mutiplicação)
Portanto, o conjunto solução X = { -3; 3; 5 }.
Analisando o segundo conjunto Y temos:
Y = {y ∈ R ¦2y + 1 = 0 e 2y2 – y – 1 = 0},
2y + 1 = 0 --> o valor de y será: y = - 1/2 = y = 0,5) " E " (as duas condições simultaneamente) 2y2 – y – 1 = 0 --> Basta encontrarmos as raízes desta equação do 2º grau. Isso pode ser feito utilizando as relações de girrard:
Dada uma equação do 2º grau ax2+bx+c=0, é possível relacionarmos as sua raízes (x1 e x2) em função dos seus coeficientes da seguinte forma:
x1 * x2 = (c/a)
x1 + x2= -(b/a)
Na equação em questão temos: a = 2; b = -1 e c = -1
portanto, y1 * y2 = -1/2 e y1 + y2 = 1/2 (lembrando que a variável em questão é y, mas poderia ser outra letra.)
Assim, as raízes da equação 2y2 – y – 1 = 0 são: y1 = 1 e y2 = -1/2
Assim, o conjunto solução Y = {-1/2}, obs: o valor y=1 não entra no conjunto solução, pois na definição do conjunto Y, temos o conectivo "e" que indica que as duas condições devem ocorrer simultaneamente, portanto, o único valor que satisfaz às duas expressões é y = -1/2.
Entre as opções, a que melhor expressa o resultado é :
X = { -3; 3; 5 } U Y = {-0,5}
c) X ∪ Y = {-3; -0,5; 3; 5}.
Gabarito, letra C.
Obrigado.
-
Nossa, realmente eu não tinha prestado atenção ao conectivo "E" no conjunto Y hehe. Muito obrigado por esclarecer, Eduardo!
-
Gente, me ajuda que eu não entendi uma coisa:
X 2 - 9 = 0
X 2 = 9
x = raiz quadrada de nove = 3
E por que o resultado é -3 ????
-
Respondendo a pergunta de Laura Fonseca:
A raiz quadrada de 9 pode ser 3 ou -3, pois ambos o números quando elevados ao quadrado tem 9 como resultado.
O número negativo quando elevado ao um expoente par, possui como resultado um número positivo e quando elevado a um expoente ímpar, resulta em um número negativo.
-
Ainda não entendi porque o 1 não entrou no conjunto solução do Y :(
-
Erick, o conjunto Y não admite o 1 pq ele não satisfaz a 1ª equação 2y+1=0.
o y tem que atender a 1ª e a 2ª equação (esse "e" aparece no enunciado do conjunto: Y = {y ∈ R ¦2y + 1 = 0 e 2y2 – y – 1 = 0})
-
Olá
Não entendi o resulta =5 gostaria de sua ajuda.
-
gilmara silva santos, está com dúvida em qual parte?
-
gente desculpa a ignorancia mas n entendi a ultima parte, a equação 2y2-y-1=0
-
Assim, as raízes da equação 2y2 – y – 1 = 0 são: y1 = 1 e y2 = -1/2
Eu não entendi porque y1 = 1 sendo que o produto e soma da equação é respectivamente -1/2 e 1/2.
-
de onde saiu esse -0 ?
-
Irei apresentar minha solução ao problema, uma vez que pode esclarecer àqueles que não conseguiram visualizar a resposta com clareza conforme a explicação do colega abaixo.
A questão desenvolver-se-á em três passos:
1) Resolução dos conjuntos individuais
2) Análise do comando da questão
3) Averiguação das respostas finais.
1) Resolução dos conjuntos iniciais.
Começando por X.
X = {x ∈ R ¦ x2 – 9 = 0 ou 2x – 1 = 9}
Legenda: V= Raíz
x²-9=0
x²=9
x=V9
x= + - 3 ( Irão me perguntar, por quê + -3 adelmo? Respondo: Quanto é -3 x -3 ? Quanto é 3 x 3? Percebo que ambos os números confirmam um mesmo resultado, que é 9)
2x-1=9
2x=10
x=5
Logo, as respostas em X são 3,-3 e 5. Perceba que o conectivo ou representa UNIDO, união. Todas as respostas são válidas.
Partindo para Y:
Y = {y ∈ R ¦2y + 1 = 0 e 2y2 – y – 1 = 0},
2y+1= 0
2y= -1
y= -1/2
2y2 – y – 1 = 0
Agora, trata-se da resolução de uma Equação do Segundo Grau. Para resolvê-la, utilizarei de dois artifícios: 1) A fórmula de Delta 2) O método de Bhaskara
Delta = B² - 4. a . c
1-4.2.-1 = Delta
Delta = 9
Bhaskara: (-b +- VDelta) /2a = R
-(-1) + - V9 / 4 = R
R = 1
R'= -1/2
Como o conjunto traz o conectivo E, apenas os resultados iguais serão válidos. Logo, apenas -1/2 valerá como resposta.
Agora, partiremos a análise das assertivas. Percebemos que nosso resultado é X U Y = { 3, -0,5 , 3 , 5 }
Logo, a acertiva correta é a Letra C
Questão suada, porém possível!
Bons estudos.
Adelmo Ribeiro
-
Thiago, o "-0,5" o "-1/2"
Apenas um está em decimal e o outro em forma de fração. Portanto -0,5 = -1/2
-
Para sabermos os elementos de cada conjunto, vamos resolver as equações dentro e cada um.
Para o conjunto x temos duas equações, resolvendo ambas abaixo:
x2 - 9 = 0 → x2 = 9 → x = ±3
2x - 1 = 9 → x = 5
Logo X = (-3; 3; 5)
Vamos agora encontrar os elementos do conjunto Y
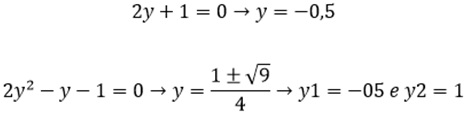
Assim, Y = (-0,5). Obs, o número 1 não entra, pois o conectivo E, exclui o mesmo. Assim fazendo X U Y obtemos(-3; -0,5; 3; 5 ).
Letra C
-
Bati na trave!!! Quaaase!! Marquei a A, pois não prestei atenção no conectivo E :(
Vivendo e aprendendo.
-
pegadinha no conectivo. essa questão vai eliminar MUITO candidato desatento.
-
se jogarmos y=1 na equação y²-y-1=0, fica ok, pois 2-1-1=0, é verdade. Mas se jogarmos y=1 na equação 2y+1=0, teremos: 2+1=0, o que não é verdade...portanto y=1 não satisfaz a condição imposta pelo conectivo E.
-
Cai igual um pato.
-
Vejamos cada conjunto:
X = {x Є R │ x – 9 = 0 ou 2x – 1 = 9}
Podemos ler esta expressão assim: o conjunto X é formado por todos os números “x” pertencentes ao conjunto dos números Reais, desde que eles obedeçam as expressões x – 9 = 0 ou 2x – 1 = 9.
Resolvendo as duas equações:
x – 9 = 0
x = 9
x = 3 ou x = -3
2x – 1 = 9
2x = 10
x = 5
Portanto X = {-3, 3, 5}.
Y = {y Є R │2y + 1 = 0 e 2y – y – 1 = 0}
Resolvendo as duas equações:
2y + 1 = 0
2y = -1
y = -1/2
2y – y – 1 = 0

y = 1 ou y = -1/2
Observe que no conjunto Y temos um “e” entre as duas equações. Ou seja, só devemos considerar os valores y que resolvem uma E TAMBÉM a outra equação. Neste caso, apenas o y = -1/2 resolve as duas equações (no conjunto X tínhamos um “ou” entre as equações, e foi por isso que consideramos todas as soluções das duas equações). Por isso,
Y = {-1/2}
Logo, nosso gabarito é:
X U Y = {-3; -0,5; 3; 5}
Resposta: C
-
https://www.tecconcursos.com.br/questoes/81407
-
primeira vez na vida que vejo '0' com sinal kkk