-
Para obter a variância da amostra:
1º Obter a média da amostra: 
= (2+3+1+4+5+3) / 6 = 3
2º Obter a variância da amostra: 
= [(2-3)² + (3-3)² + (1-3)² + (4-3)² + (5-3)² + (3-3)²] / 6-1
=10 / 5 = 2
-
A colega Sheila fez um excelente trabalho.
A média da amostra é aritmética (existem tb média harmônica, ponderada, mediana etc) (2+3+1+4+5+3)/6= 18/6= 3
Variãncia= A média aritmética é subtraída por cada membro, elevado a ² e dividido pelo n° de componentes -1.
(2-3)^2+(3-3)^2+(1-3)^2+(4-3)^2+(5-3)^2+(3-3)^2/6-1=
1+0+4+1+4+0/5==10/5=2
-
Basta usar a equação da variância para um rol, lembrando que é amostra (divide-se tudo por n - 1 e não por n!!!!).
(1 / 5) x ( 64 - ( 18 ^ 2 / 6) ) = 2
Resposta: Letra B.
-
Esta
questão requer que o candidato demonstre conceitos fundamentais sobre
estatística básica.
Inicialmente, a média aritmética
(
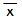
) é a razão entre a soma de todos os
valores observados e o número total de observações. Assim:
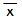 = ( 2 + 3 + 1 + 4 + 5 + 3) / 6 =
18/6 = 3
= ( 2 + 3 + 1 + 4 + 5 + 3) / 6 =
18/6 = 3
Finalmente, calcula-se a
variância (s²), que é uma medida de dispersão que mede o quanto cada elemento
de uma distribuição se desviou de um valor central.
s²
= (2-3)² + (3-3)² + (1-3)² + (4-3)² + (5-3)² + (3-3)² / (6 -1)
s²
= 1 + 0 + 4 + 1 + 4 + 0 /5
s²
= 10/5 = 2
Resposta
B
-
Rol : 2, 3, 1, 4, 5, 3 = 1, 2, 3, 3, 4, 5. (n = 6 elementos)
Memória de cálculo:
∑Xi ² = 1² + 2² + 3² + 3² + 4²+ 5² = 64
(∑Xi) ² = 1+2+3+3+4+5 = 18 ---> (18)² = 324
Aplicando a fórmula desenvolvida da Variância:
1/n * [ ∑Xi ² - ( ∑Xi )² ] ( Se o enunciado falar de amostra, primeira parte da fórmula subtrai - 1)
(1/n-1) * [ ∑Xi ² - ( ∑Xi )²/n ]
1/6-1 * [ 64 - 324/6 ]
1/5 * 60/6 (simplifica 60/6 = 10 e divide 10/5) = 2
= 2
-
Uma forma de calcular a variância populacional é:

Assim,

Resposta: B
-
A variância é a média aritmética dos quadrados dos desvios.
• Para calcular a variância, devemos:
− 1º passo (MÉDIA): tirar a média de todos os números;
− 2º passo (TIRAR A DIFERENÇA): subtrair o valor da média, de cada número da lista;
− 3º passo (QUADRADOS): elevar ao quadrado cada valor obtido da subtração; e
− 4º passo (MÉDIA DOS QUADRADOS): calcular a média dos valores elevados ao quadrado e dividi-los por n-1, se
amostral, ou só por n, se for populacional, onde n é a quantidade de elementos.