-

Atentar para a parte achurada em azul. Pois podemos ter essa possibilidade, porém, não podemos ter essa afirmação. No entanto, podemos afimar a parte vermelha com certeza, e a parte amarelada no mínimo (ou teremos essa parte em amarelo mais a azul, podemos ter essas possibilidades). Com certeza temos professores que não são políticos, e essa certeza, se dá pela parte que está em vermelo!
até mais!
;)
-
Alguns políticos são ricos e nenhum professor é rico, então pode-se afirmar, com certeza, que da classe de políticos, alguns não são professores, pois os professores não são ricos.
Bons estudos!
-
Peço licença Diego para usar seu gráfico, fantástico diga-se de passagem.
Acertei a questão.Mas dizer nas as afirmativas que: (b) Alguns professores são políticos; e (c) Alguns políticos são professores, não são a mesma 'coisa"?
Essa coisa, não seria o campo de inseção azul de professores, pois nenhum são ricos, e políticos?

-
Mazzia, as letras b) e c) são a mesma coisa, sim. Dizer que alguns professores são políticos é o mesmo que dizer que alguns políticos são professores.
Mas é como o próprio Diêgo Lima disse: “Atentar para a parte achurada em azul. Pois podemos ter essa possibilidade, porém, não podemos ter essa afirmação. No entanto, podemos afirmar a parte vermelha com certeza...”
A parte em azul (do diagrama feito pelo Diêgo) representa as alternativas b) e c), porém são possibilidades e não uma certeza. Mas a letra d) - alguns políticos não são professores - é uma afirmação certa.
Força e fé nos estudos!
-
Na minha opinião estaria correta 2 opções de entendimento
1-Alguns professores não são políticos
2-Alguns políticos não são professores.
Avante!!!
-
LETRA D - "Alguns políticos não são professores"
Nenhum professor é rico - Logo o conjunto dos PROFESSORES e dos RICOS não tem nenhum elemento em comum (não há intersecção)
Alguns políticos são ricos - O conjunto dos POLÍTICOS e dos RICOS têm alguns elementos em comum. Esse elementos em comum não poderão ser PROFESSORES, pois nenhum professor é rico, assim os POLÍTICOS que são RICOS, não serão professores, portanto:
ALGUNS POLÍTICOS (os ricos) NÃO SÃO PROFESSORES
Fred, na sua opção 1, o conjunto de professores pode estar contido no conjunto de políticos sim, só não irá ter elementos em comum com o conjunto dos ricos, limitando-se aos "políticos não ricos"... Portanto poderia: "Todos os professores são políticos" (sendo que não poderia ser incluído dentro do conjunto dos professores os políticos ricos)
-
Bom dia!
Para o entendimento da questão é muito interessante a construção dos diagramas, mas daria p resolver mais rapidamente só olhando as respostas. Vejamos: a letra "b" é a mesma coisa que a letra"c" (logo se anulam, pois se não teríamos duas respostas corretas) e a letra"a" é a mesma coisa que a letra "e". Dessa forma, resta somente a letra d. Já observei duas vezes isso acontecendo nas provas da ESAF.
Bons estudos!
-
Nenhum professor é rico.
Alguns políticos são ricos.
O que relaciona as duas premissas acima é a palavra RICO
portanto RICO e POBRE são nossos conjuntos, e os elementos dos conjuntos são PROFESSOR E POLITICO;
Montemos os conjuntos:
Rico: {políticos}
Pobre: {políticos; professores}
*Veja que a sacada da questão não está na intersecção dos conjuntos, mas na compreensão de que os elementos do conjunto são profissões, logo atreladas a pessoas.
Portanto podemos expandir os conjuntos:
Rico: {políticos}
Pobre: {políticos; professores; políticos/professores}
a) Nenhum professor é político.
Pobre: {políticos; professores; políticos/professores} - ERRADO, pois pode haver políticos/professores
b) Alguns professores são políticos.
Pobre: {polìticos; professores; políticos/professores} - CERTO, mas não tem como ter certeza, pois a suposição políticos/professores pode não existir;
c) Alguns políticos são professores.
Pobre: {políticos; professores; políticos/professores} - CERTO, mas não tem como ter certeza, pois a suposição políticos/professores pode não existir;
d) Alguns políticos não são professores.
Rico: {políticos} - CERTO.
e) Nenhum político é professor.
Pobre: {políticos; professores; políticos/professores} - ERRADO, pois pode haver políticos/professores
-
Essa questão pode ser resolvida de duas maneiras.
A primeira é por exclusão das alternativas
A = E
B = C
Então só nos resta a alternativa D.
A segunda maneira é pelo Diagrama de Venn. No entanto, discordo do diagrama apresentado e comentado pelo colegas.
-
Sobre as Alternativa B e C, entendi da seguinte forma:
B-) Alguns Professores são politicos; (por mais que alguns politicos não sejam ricos, nada obriga que alguns Professores sejam Politicos)
C-) Alguns Politicos são Professores: (por mais que os Professores não sejam Ricos, nada obriga que alguns Politicos sejam Professores)
Agora:
D) Alguns Politicos não são Professores: (Podemos afirmar com certeza; pois alguns politicos que são Ricos, com certeza não vão ser Professores)
-
Gente! eu achei essa questão absurda! alguém me ajuda. como pode haver apenas 1 certa?
vamos a minha dúvida como b e c são falsas? se nenhum professor é rico, porém alguns políticos sao ricos. então a B não está correta ao afimar que ALGUNS PROFESSORES SÃO POLITICOS???? e a mesma coisa em relação a letra C ???
-
Em uma cidade as seguintes premissas são verdadeiras: Nenhum professor é rico. Alguns políticos são ricos. Então, pode-se afirmar que:
Traduzindo: Professor é pobre e ALGUNS políticos são ricos. (aqui eu troquei para pobre, mas nem sempre dá p/ fazer isso) Se ALGUNS (NÃO TODOS) políticos são ricos ALGUNS são pobres então entre os políticos pobres PODE ou Não ter algum que além de político é professor, PODE = suposição e suposição está só na imaginação _ Já dá para tirar a A, B, C, E _ Porém é certo que ALGUNS políticos (Todos os ricos) NÃO são professores, está escrito no enunciado que NENHUM professor é RICO, não está na imaginação! Letra D
-
GENTEEM O PRÓPRIO POLÍTICO QUE É RICO, NÃO SERÁ PROFESSOR, JÁ QUE NENHUM PROFESSOR É RICO...
GABARITO ''D''
-
usei a técnica do professor renato, se você observar a letra A anula a E e a B anula a C
-
As alternativas se anulam. Só sobra uma.
-
Para quem gosta de resolver por diagramas, fica bem simples. Partindo do que diz a questão: Nenhum professor é rico. Alguns políticos são ricos...
Você desenha o conjunto dos ricos, pegando parte dele, o dos políticos. Agora o dos professores pode ocorrer dois casos: pegando parte do conjunto dos políticos OU fora de todos os conjuntos (ricos e políticos). Isso já resolve a questão. Pois ao analisar o diagrama feito, só pode concluir que: alguns políticos não são professores. Estejam os professores em qualquer uma das formas que apresentei acima.
Gabarito D
-
NENHUM E ALGUM, resolvo assim:
Nenhum professor é rico.
Alguns políticos são ricos.
1º Cortamos as partes de que repetem: (é rico/são ricos),
Nenhum professor (é rico)
Alguns políticos (são ricos).
2º: Entre nenhum e algum, prevalece o algum
Nenhum professor
Alguns políticos
3: e acrescenta-se um NÂO:
a frase fica: algum politico NAO é professor
-
Dica que aprendi:
-a gente desenha o que o texto diz!
-mas temos que supor uma possibilidade que não está escrita no comando!
-a questão nao me proibiu de pensar que pode haver um político que seja professor, então eu imagino que PODE existir!
-
Se nenhum professor é rico, então tem político (alguns que fazem intersecção com o grupo dos ricos) que não são professores.
GABARITO D
-
Alguns políticos não são professores. Porq esses políticos são ricos, e não há professor rico.
-
Vamos utilizar os conjuntos dos “professores”, dos “políticos” e dos “ricos”. Temos, a princípio,
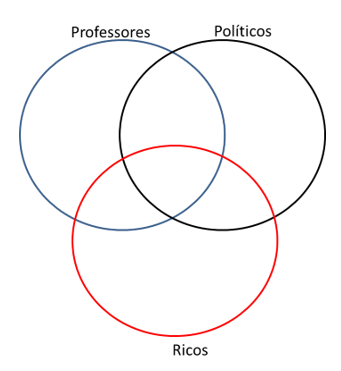
Como nenhum professor é rico, esses dois conjuntos não tem intersecção (região em comum). E como alguns políticos são ricos, esses dois conjuntos tem intersecção. Corrigindo nosso diagrama, ficamos com a figura abaixo:
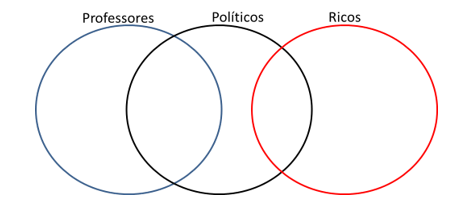
Analisando as opções de resposta:
a) Nenhum professor é político. → ERRADO. Pode haver elementos na intersecção entre esses dois conjuntos.
b) Alguns professores são políticos. → ERRADO. Embora possa haver elementos nessa intersecção, não podemos garantir que eles de fato existem. Pode ser que nenhum professor seja político.
c) Alguns políticos são professores. → ERRADO, pelos mesmos motivos do item anterior.
d) Alguns políticos não são professores. → CORRETO. Os políticos que também fazem parte do conjunto dos ricos certamente NÃO são professores.
e) Nenhum político é professor. → ERRADO, pelos mesmos motivos da alternativa A.
Resposta: D