-
Fiz assim...
------->Números divisíveis po 3 = (3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99)
_______________________________________________________________________________________________________--
------->Números divisíveis po 8 = (8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96)
Logo, P(3)=33/100 e P(8)=12/100
JOGADA: Como a questão interpela o OU, é soma beleza? Agora é só somar 33/100 e 12/100? Não! Pois temos as possibilidades de números (no sorteio) que são divisíveis por 8 e 3 ao mesmo tempo. São eles: (24, 48, 72 e 96)=4 números em 100. Logo a resposta será:
P(3)+P(8)-P(3)eP(8)=(33/100)+(12/100)-(4/100)=41/100 ou 41% (letra A)
até mais!
;)
-
Muito bom... Parabéns, Diêgo Lima!
Você - ou outro colega - sabe dizer se há uma fórmula para encontrar, neste caso, quantos números são divisíveis por 3 ou por 8, numa lista 1 a 100?
Para não ter que fazer no braço, pois a banca pode trazer "numa lista de 1 a 1000" e na prova cada minuto é imporante!
Obrigado!
-
Olá Breno Setuba, você pode usar progressão aritmética:
an = a1 + (n - 1).r
onde:
an = último termo;
a1 = primeiro termo;
n = número de termos;
r = razão
Então para achar a quantidade de termo divisivel(dividir e deixar resto zero) por 3 entre 1 e 100, você precisa saber desses qual é o primeiro termo divisivel por 3, que é lógico que é o próprio 3, pois 1 e 2 sem chance né. Precisa saber também o último termo divisível por 3, vamos lá com calma utilizando a eliminação, 100 fora, 99 ok(macete, para um número ser divisível por 3, a soma dos seus algarismos tem que dar um número divisível por 3. 99---->9 + 9 = 18-------->18:3 = 6).
Com base nessas informações podemos utilizar a fórmula da PA, para acharmos o números divisível por 3, entre 1 e 100.
an = 99 a1 = 3 n = ? (o que queremos achar) r = 3 ( a razão é o próprio n°, pois de 3 em 3 sempre haverá um n° divisível por 3)
an = a1 + (n - 1).r 99 = 3 + (n - 1).3 99 = 3 + 3.n - 3 99 = 3.n n = 99/3 n= 33
Agora amigão utilizamos o mesmo raciocínio para encontrar os números divisível por 8 entre 1 e 100. Encontraremos:
an 96 a1 = 8 n = ? r = 8
an = a1 + (n - 1).r 96 = 8 + (n - 1).8 96 = 8 + 8.n - 8 96 = 8.n n = 96/8 n =12
Breno, com isso vemos que de 1 até 100, temos 33 n° divisível por 3 e 12 n° divisível por 8, mas como bem frisou nosso amigo Diêgo Lima, entre esses n° há os que são comuns, ou seja, ao mesmo tempo divisível por 3 e 8, portanto não podemos contá-los duas vezes, Ok?
Espero ter ajudado.
Grande abraço.
-
LETRA A - 41%
+ Divisíveis por 3: 100 / 3 = 33 (despreza-se o resto, pois este não é divisível)
+ Divisíveis por 8: 100 / 8 = 12 (despreza-se o resto, pois este não é divisível)
Porém nessa sequência há números que se repetem, que são divisíveis tanto por 3 quanto por 8, que corresponde ao M.M.C. (Mínimo Múltiplo Comum) de 3 e 8 = 24, portanto devemos subtrair esses números que se repetem:
- Divisíveis por 24: 100 / 24 = 4 (despreza-se o resto, pois este não é divisível)
Portanto tem-se que 33 + 12 - 4 = 41 números de 1 a 100 são divisíveis por 3 e 8:
41/100 = 41%
-
PUTZ!! resolução ninja do Dani!!.. Que é isso cara.. nem sabia desse macete!!
-
Neste caso basta utilizar a formula de união de probabilidades. O conjunto A possui 33 possibilidades de múltiplos de 3; o conjunto b tem 12. E a intersecção (∩) entre os dois conjuntos possuem 4, que são: 24, 48, 72 e 96.
P(aUb)=P(a)+P(b)-P(a∩b)
P(aUb)= 33/100 + 12/100 - 4/100
P(aUb)=41/100
P(aUb)= 41%
-
Primeiramente definimos nosso espaço amostral:
100 chances
Queremos:
P(A) OU P(B) = P(A) + P(B) - P ( A ^ B)
P(A) = Ser divisível por 3
Por progressão aritmética de razão 3, definimos quantos números são.
An = A1 + ( N - 1) . R
99 = 3 + ( n -1) . 3
99 = 3 +3n -3
3n =99
n =33
Então P(A) = 33 chances em 100 = 33/100
P(B) = Ser divisível por 8
Analogamente
96= 8 + (n-1) . 8
88 = 8n -8
96 =8n
n= 12
Então P(B) = 12/100
P( A ^ B) = Ser divisível por 3 e 8 ao mesmo tempo
MMC = 24
24,48, 72,96 = 4 chances
P ( A ^ B) = 4/100
Então
P( A ou B) = 33 + 12- 4 / 100 = 41%
-
Divisível por 3 => 100/3 =33
Divisível por 8 => 100/8 = 12 (aproximadamente)
Divisível por 24 => 100/24 = 4
33 + 12 = 45 - 4 = 41
-
Eu tava tentando ENTENDER o porque desse 24. E nego só dando fórmula, maneiras etc. A unica explicação foi a da Dani mesmo. Entendi porque deve se subtrair por 24. Nem os comentários nem o professor do Qconcursos explicam. ai vc fica na dúvida se sempre tem que fazer isso e em quais situaçôes.
-
De 1 a 100 temos um total de 100 números.
O primeiro número divisível por 3 é o próprio 3. A partir daí, basta irmos somando 3 unidades para obter os demais números divisíveis por 3, até chegar no 99, que é o último. O total de múltiplos de 3 que temos de 3 a 99 é:
Divisíveis por 3 = 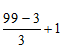
Divisíveis por 3 = 33
Veja que eu somei 1 unidade na conta acima para contabilizar as duas extremidades. Quando fazemos simplesmente (99 – 3) / 3, estamos contando apenas um dos extremos (o 99 ou o 3).
O primeiro número divisível por 8 é o próprio 8. A partir daí, basta irmos somando 8 unidades para obter os demais números divisíveis por 8, até chegar no 96, que é o último. O total de múltiplos de 8 que temos de 8 a 96 é:
Divisíveis por 8 = 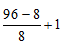
Divisíveis por 8 = 12
Somando os números divisíveis por 3 com os divisíveis por 8, temos 33 + 12 = 45 possibilidades. Ocorre que ao fazer isto estamos somando duas vezes os números que são divisíveis por ambos (3 e 8). Portanto, precisamos subtrai-los uma vez.
Os números divisíveis simultaneamente por 3 e por 8 são os números divisíveis por 24, que é o mínimo múltiplo comum entre eles. Portanto, temos os números 24, 48, 72 e 96, totalizando 4 números. Subtraindo-os, ficamos com:
45 – 4 = 41 possibilidades
Assim, dos 100 números possíveis, 41 são divisíveis por 3 ou por 8 (ou por ambos). A chance de escolher um deles é:
P = 41 / 100 = 41%
Resposta: A
Obs.: repare que você gastaria poucos minutos para resolver esta questão manualmente, simplesmente listando os números de 1 a 100 que são divisíveis por 3 ou por 8. Às vezes é mais rápido partir para a solução “braçal” do que ficar bolando alguma solução “inteligente”.
-
Consegui fazer usando a UNIÃO DAS PROBABILIDADES:
P(A U B) = P(A) + P(B) – P(A ∩ B).
P( DIV/3 U DIV/8 )= P( DIV/3 ) + P( DIV/8) - P( DIV/3 ∩ DIV/8 )
100/3 + 100/8 - MMC( 3, 8)
33 + 12 - 100/24
45 - 4
41
OBS:
P( DIV/3 ∩ DIV/8 )=
P(DIV/3) X P(DIV/8)
3 X 8
24
Não sei. Só sei que foi assim!!!