-
Questão trata-se de uma combinação.Cn,s = n!/s!*(n-s)!Chamaremos H4,1 a combinação em que aparecerá um homem.Chamaremos H4,2 a combinação em que aparecerão dois homens.Chamaremos M6,1 a combinação em que aparecerá uma mulher.Chamaremos M6,2 a combinação em que aparecerão duas mulheres.Fica assim:H4,1 * M6,2 = 60H4,2 * M6,1 = 36Logo 60 + 36 = 96Alternativa correta: "C"
-
Para que tenhamos pelo menos um homem e pelo menos uma mulher na equipes, só pode ser:1) 2 homens e 1 mulher => C4,2 . 6 = 6 . 6 = 362) 2 mulheres e 1 homem => C6,2 . 4 = 15 . 4 = 60Opções (pelo menos um homem e pelo menos uma mulher) = 36 + 60 = 96
-
O TOTAL de grupos formados (sem considerar a necessidade de ter 1 homem e 1 mulher) é: C10,3 = 120.Se preciso ter 1 homem e 1 mulher no grupo, NÃO posso formar grupos com 3 mulheres nem grupos com 3 homens.Então, vejamos quantos grupos poderíamos formar com exatamente 3 mulheres (a) e com exatamente 3 homens (b).a) C6,3 = 20b) C4,3 = 4Para saber, então, quantos grupos podemos formar com pelo menos 1 homem e 1 mulher, é só subtrairmos (a) e (b) do total: 120-20-4 = 96.
-
Possibilidade A : 1 homem 2 mulheres
Homem = C41= 4! = 4
1!3!
Mulher = C62= 6! = 15
2!4!
Possibilidade B : 2 homens 1 mulher
Homem = C42= 4! = 6
2!2!
Mulher = C61= 6! = 6
1!5!
4 multiplicado por 15 =60 +36=96
-
Eu uso praticamente sempre o mesmo modelo para resolver essas questões:
PRIMEIRO: Saber se é Arranjo ou Combinação
SEGUNDO: Caucular as possibilidades sem as restrições que o problema coloca.
TERCEIRO: Subtrair Todas possibilidades pelas restrições:
__
PRIMEIRO: M-M-H OU H-H-M OU H-M-H OU M-H-M A ordem NÃO importa, então CombinaÇÃO.
SEGUNDO: C10,3= 120
TERCEIRO: não podemos ter apenas mulheres, nem apenas homens
Todas mulheres C6,3= 20
Todos Homens C4,3= 4
TERCEIRO:
120 - 20 - 4 = 96
Letra C
-
Questão simples. Basta raciocinar que o grupo pode ser de: dois homens e uma mulher ou duas mulheres e um homem. Tendo isso em mente é só formar as combinações.
1 homem e 2 mulheres:
C(4,1)*C(6,2) = 4*15=60
2 homens e 1mulher:
C(4,2)*C(6,1) = 6*6=36
Agora é só somar as duas possibilidades e chega-se ao resultado.
36+60=96
-
Questão básica. Boa para revisar a essência da combinação com equipes.
Dado da questão: Pelo menos 1 mulher e 1 homem na equipe de 3 funcionários. Teremos aí, então, 1H e 1M estáticos.
Hipóteses: reparem que nas duas hipóteses abaixo estaremos respeitando o que a questão pede que é ter PELO MENOS 1H e 1M.
I) 1H e 2M
II) 2H e 1M
Feito isso, basta pegar o número de homens que temos disponíveis e o número de mulheres e combiná-los com as hipóteses, portanto:
I) C4,1 (4H disponíveis para 1H da hipótese) = 4
C6,2 (6M disponíveis para 2M da hipótese) = 15
Multiplica-se: 15x4 = 60
II) C4,2 (4H disponíveis para 2H da hipótese) = 6
C6,1 (6M disponíveis para 1M da hipótese) = 6
Multiplica-se: 6x6 = 36
Feito a combinação das hipóteses com os disponíveis, somam-se os resultados: 60+36 = 96 Gab. C
-
Prezados,
Sejamos páticos:
Quando a questão menciona a seguinte passagem "havendo na equipe pelo menos um homem", isso significa dizer que a equipe não pode ser formada SOMENTE por mulheres. Igualmente, quando a questão menciona "(...)e pelo menos uma mulher", significa dizer que não pode existir uma equipe formada SOMENTE por homens.
Em resumo:
i) Pelo menos 1 homem = Já não pode ser equipe de mulheres apenas (C4,3)
ii) Pelo menos 1 mulher = Já não pode ser equipe de homens apenas (C6,3)
------------------------------------------------------------------------------------------------------
Logo, as maneiras de combinarmos seria pegar TODAS as combinações possíveis e excluir apenas os casos citados nos itens (i) e (ii).
C10,3 - C4,3 - C6,3 = 120 - 4 - 20 = 96//
Gab.: Alternativa "c"
-
Apenas duas possibilidades para as equipes: Um homem e duas mulheres, ou uma mulher e dois homens.
4 x 6 x 8 / 2* (*combinações repetidas) = 96
-
Se a equipe tem 3 pessoas, precisa ter pelo menos 1 homem e 1 mulher, temos 2 possíveis grupos: 2 homens e 1 mulher, ou 2 mulheres e 1 homem. Vejamos quantas possibilidades temos para cada tipo de grupo.
2 homens e 1 mulher:
Para escolher 2 homens em um total de 4 disponíveis, basta calcular a combinação de 4, 2 a 2:
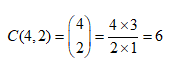
E para escolher 1 mulher em um total de 6, temos 6 possibilidades, como você pode comprovar abaixo:

Pelo princípio fundamental da contagem, temos 6 x 6 = 36 formas de agrupar 2 homens e 1 mulher.
2 mulheres e 1 homem:
Para escolher 2 mulheres em um total de 6 disponíveis, basta calcular a combinação de 6, 2 a 2:

E para escolher 1 homem em um total de 4, temos 4 possibilidades, como você pode comprovar abaixo:

Pelo princípio fundamental da contagem, temos 15 x 4 = 60 formas de agrupar 2 mulheres e 1 homem.
Assim, ao todo temos 36 + 60 = 96 equipes distintas com 3 funcionários, respeitando as condições do enunciado.
Resposta: C