-
| x | y | x^y | x v y | x=>y | ~x | ~y | ~x v ~y | y=>(x=>y) | (~x v ~y) ^ (y=>(x=>y) | x ^ ~x |
| v | v | v | v | v | f | f | v | v | v | f |
| v | f | f | v | f | f | v | v | v | v | f |
| f | v | f | v | v | v | f | v | v | v | f |
| f | f | f | f | v | v | v | v | v | v | f |
resolvendo a tabela verdade, resolve-se a questão!
bem trabalhosa...
-
Questãozinha chata!
-
Se vc se contradiz, vc é e não é algo ao mesmo tempo, então não há como haver uma contradição sem uma negação.
São contradições: A então não A; A e não A.
-
Para mim a letra "E' também está correta
Neste exemplo:
(A ^ B) u (A u ~A) é uma tautologia e só possui os conectivos de disjunção e conjunção
-
Letra C de Com certeza vocÊ terá que estudar muito, nessa eles pegaram mais pesado...
-
E) Existem tautologias que só possuem os conectivos de disjunção e conjunção: (v) e (^)
(A ^ B) v (¬A)v(¬B)
![]()
![]()
-
Nesse caso a banca considerou a negação como conectivo e deixou isso bem claro na questão .
É o tipo de questão que deve ser lida algumas vezes , então é melhor deixar para o final da prova .
-
Renato...e se tivermos X, Y e Z?
-
A LETRA "E" NÃO ESTA CORRETA POIS A BANCA CONSIDEROU O MODIFICADOR LÓGICO COMO CONECTIVO.
-
Depois de errar e refletir, percebi o que o examinador quis dizer... Na verdade, de que forma ele quis confundir o candidato: Citou que uma tautologia pode ser composta apenas pelos conectivos, sendo que, sem elementos, não há tautologia!!!! Elementos são o "cerne" da proposição
-
COMENTÁRIO:
Para resolver essa questão, desenha-se
a tabela verdade e aplica-se um contra exemplo a cada
alternativa, até encontrarmos a verdadeira, assim:
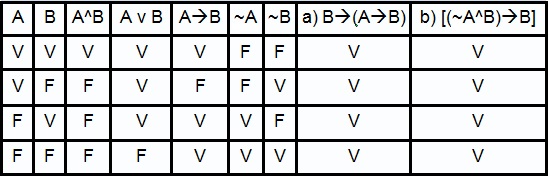
a)
Alternativa falsa, pois encontramos um contra exemplo que contradiz a
afirmação.
b)
Alternativa falsa, pois encontramos um contra exemplo que contradiz a
afirmação.
c) Alternativa correta, pois pela definição, Contradição
é toda proposição cujo valor lógico não é tautológico. Singelamente, é possível
afirmar que a contradição consiste na afirmação e negação simultâneas de uma
mesma coisa, na mesma decisão.
Letra C.
-
Tipo de questão que deve-se prestar atenção no enunciado.
Letra E, está errada pois o examinador deixou claro que negação tbm deve ser considerado conectivo.
Sendo assim, não existem Tautologias sem negação. Letra C !
-
c) Não existem contradições sem que ocorra o conectivo de negação.
Descordo pois (P <-> Q) <-> (P v Q)
Não tem negação e é contradição
Não é?
-
EXEMPLOS QUE SE ELIMINA, DE PRIMEIRA, A LETRA E:
Pv(~P)
P->P
P<->P
Pv(~P)
TODOS ESSES EXEMPLOS GERAM UMA TAUTOLOGIA
FÉ EM DEUS E BONS ESTUDOS!
-
c) Alternativa correta, pois pela definição, Contradição
é toda proposição cujo valor lógico não é tautológico. Singelamente, é possível
afirmar que a contradição consiste na afirmação e negação simultâneas de uma
mesma coisa, na mesma decisão.
-
Como se resolve isso no papel? Tem que inventar as formulas ate achar alguma que elimine a alternativa? kkkk
-
CONSIDERE = VUNESP solicitou SOMENTE (E, OU e SE...ENTÃO) para está questão especificamente.
==================================================================================================
os operadores lógicos : (se...e somente se) e o (ou exclusivo) não foram considerados,pela VUNESP, nesta questão conoforme enunciado. " Considerando os conectivos usuais de negação, disjunção (inclusiva), conjunção e implicação (material)"
==================================================================================================
Montando a seguinte tabela:
============================================================================================================
P Q E OU SE... ENTÃO
V V V V V
V F F V F
F V F V V
F F F F V
Logo,
c) Não existem contradições..........sem que.......ocorra o conectivo de negação.
não existe falso..................sem que.......ocorra uma falsidade.
apenas a linha V V que sempre teve como resultado V
-
Pessoal, não é válida a proposição composta (p<->q)^(p v q), pois o enunciado disse:
"Considerando os conectivos usuais de negação, disjunção (INCLUSIVA), conjunção e implicação (material), assinale a alternativa correta."
-
(p q) ^ (p v q)
P Q (p<---> q) (p v q) (p<--> q) ^ (p v q)
V V V F F
V F F V F
F V F V F
F F V F F
Ícki Φ ,você não esta usando uma disjunção inclusiva ( V ) conforme o enunciado pede e sim uma disjunção EXCLUSIVA ( v ).
Nosso colega Gaio Quaresma está correto.
-
Sacanagem pedirem 50% de aproveitamento em cada matéria no concurso da policia civl SP/2018. Principamente em raciocinio lógico, uma vez que tal disciplina não se mostra essencial para a carreira policial, bem como não avalia a inteligência do candidato.
-
A) Não existem tautologias só com o conectivo de implicação.
Realmente, existem tautologias com outros conectivos tbm.
#interpretação
Pode dar essa ideia tbm né , o "só"? Ou to enganada...
-
Vejamos cada alternativa:
a) Não existem tautologias só com o conectivo de implicação.
ERRADO. A condicional p-->p é uma tautologia.
b) Não existem tautologias com o conectivo de conjunção.
ERRADO. A proposição abaixo tem o conectivo conjunção, e é uma tautologia: (p e p) --> p.
c) Não existem contradições sem que ocorra o conectivo de negação.
CORRETO. Repare que sempre que escrevemos uma contradição, ela contém a negação: “p e ~p”, “p se e somente se ~p” etc. Alguns autores entendem que existem contradições sem a negação, como: “sou gordo e sou magro”. Em tese essa é uma contradição sem o uso da negação. Mas repare que é possível interpretar que ser magro é a negação de ser gordo (se só existirem essas duas classificações), de modo que “sou magro” na verdade significa “não sou gordo”, ou seja, essa frase seria “sou gordo e não sou gordo”, contendo, ainda que implicitamente, o conectivo de negação.
d) Não existem contradições com apenas uma letra sentencial (considerando que ela pode ser utilizada mais de uma vez).
ERRADO. A frase “p e ~p” é uma contradição com apenas uma letra sentencial.
e) Existem tautologias que só possuem os conectivos de disjunção e conjunção.
ERRADO. Observe que tautologias usando a disjunção e/ou a conjunção, como “p ou ~p” e “(p e p) --> p”, sempre usam também outro conectivo.
Resposta: C
-
Não existem contradições sem que ocorra o conectivo de negação ????
Dá para fazer a contradição de uma proposição utilizando o conectivo (ou...ou) também.
Exemplo: OU P OU P= FALSO
Disjunção exclusiva só será verdadeira se forem diferentes.
-
reparem no enunciado ! ele nao menciona disjunção exclusiva.
-
Eu não entendi a explicação de porque a E está errada. Alguém tem um exemplo com frases?
-
Lembrem-se de que P v ~ P é sempre TAUTOLOGIA.
-
Alguém poderia me explicar a D e a E ? pq estão erradas ?
-
GAB: C
Não existe contradições sem que ocorra o conectivo de negação.
Isso se dá porque, ao analisarmos os conectivos considerados pela questão (ou; e; se... então), não existe situação em que, para que ocorra uma contradição, não haja pelomenos uma preposição negativa.
Para o conectivo "ou" ter valor negativo deve-se ter as duas preposições negativas;
Para o conectivo "e" deve-se ter pelo menos uma das preposições negativas;
Para o conectivo "e... então" deve-se ter o consequente negativo.
-
https://www.youtube.com/watch?v=ilUE1jPP0V4&t=1903s MIN 24:05
-
Gabarito: C
-
Por menos questões assim kkkkkk
-
que negócio é esse tautologia? chato mesmo!
-
Aprendi que: "Está claro e está escuro" é uma contradição e não possui conectivo de negação, ou seja, não entendi essa matéria ainda.
-
solução compacta:
A: errada, por conta de "p --> p"
B: errada, por conta de "~(p e ~p)"
C: correta, propriedade da negação
D: errada, por conta de "p e ~p"
E: errada, mesmo motivo da letra C.