-
Item certo!
É caso de combinação, pois a ordem dos agentes não faz diferença na formação das equipes. A equipe formada por A, B e C é a mesma da formada por B, C e A.
Cn,p = n! / p! x (n - p)!
C12,3 = 12! / 3! x (12 - 3)! = 12x11x10x9! / (3x2x1) x 9! = 12x11x10 / 6 = 220.
-
Quantidade de maneiras de se formar 4 equipes de 3 agentes: idem resposta da questão Q307256
-
Uma maneira mais rápida de se resolver:
Como essa combinação não depende de ordem, podemos fazer o seguinte:
12 x 11 x 10 (Mas, como a ordem não importa, temos que dividir)
Como são 3 agentes por equipe:
12/3 x 11/2 x 10/1 = 220
-
Gente, não tá havendo uma confusão aí não?
No meu entendimento a resposta seria 220, caso fosse para criar uma única equipe contendo 3 agentes partindo-se de um grupo de 12 agentes, mas não foi isso que eu entendi. A questão diz que a unidade policial com 12 agentes ... se cada equipe formada por 3 agentes...a quantidade de maneiras diferentes de se formar essas equipes...
Entendi que todos os 12 agentes seríam utilizados em alguma equipe de 3 pessoas. Serão 4 equipes de 3 agentes cada uma. Isso, de fato, remete à Q307256.
C(12,3) * C(9,3) * C(6,3) * C(3,3) = 369.600
A resposta no final das contas não é alterada, mas pode ser diferente para uma outra questão.
-
Concordo com o RWerneck. O pessoal tá colocando a resposta para apenas uma única equipe.
-
Galera, também concordo com o RWerneck.
Bons estudos a todos.
-
tambem... não entendi essa questão naõ...
bons estudos kkkk
-
Pessoal, não tem problema nenhum na questão e muito menos nas resoluções dada pelos colegas.
A banca só colocou "equipes" no final porque no contexo estava da mesma forma...fora isso é uma simples questão de Análise Combinatória. Onde "equipes" e "equipe", concluiriamos que a questão está CERTA do mesmo jeito!!!rs
-
C 12, 3= 220
-
A análise combinatória pode-se dar de duas formas: Combinação: É quando a ordem dos elementos do grupo não importa. Por exemplo, quero montar um grupo de 3 pessoas, que se chamam Maria, Pedro e Paula. Nesse caso, a ordem não importa, serão as mesmas pessoas dentro do mesmo grupo, só conseguiria realizar de uma única forma. Arranjo: A ordem do grupo é importante. Normalmente cai nas questões falando sobre competições, escolha de pessoas para colocação de cargos etc. Exemplo: Campeonato de futebol entre 3 times, onde o Flamengo é o 1º colocado, Botafogo em 2º e o Vasco em 3º. Nota-se que a posição dos times é importante, se o Botafogo ficasse em 1º, já seria uma combinação diferente. Questões de arranjo, não dividimos pelo fatorial, apenas multiplicamos as possibilidades. Precisamos entender também o que é fatorial? Vamos lá: Permutação: É a ideia de que objetos distintos podem ser arranjados em inúmeras ordens diferentes. Aparece em questões normalmente como: Arrumar, anagrama e não lembra a ordem. Ex: Fatorial 5! = 5.4.3.2.1= 120 3! = 3.2.1= 6 Voltando para questão, o caso é de análise combinatório por combinação, teremos que formar os 4 grupos e dividir por seu fatorial: Grupo 1= 12.11.10 / 3! = 220 (Lembrando que 3! é igual a 6) OBS: De cara já matáriamos a questão, pois desde o primeiro grupo o resultado já seria superior a 200, não seria necessário continuar até o final para responder a questão, mas vamos continuar para melhor entendimento. Grupo 2= 9.8.7 / 3! = 84 ( Como a 12º, a 11º, a 10º, já foram colocadas da orgarinazão de grupos anterior, partimos para as proximas que são a 9º, 7º e 8º) Grupo 3= 6.5.4 / 3! = 20 Grupo 4= 3.2.1 / 3! =1 Agora multiplicamos todos os resultados, para termos todas as possibilidades de combinação: 220.84.20.1 = 369.600. Não desanimem!! A questão é simples, os calculos podem ser simplificados, com prática, vocês poderão resolver questões desse tipo com agilidade e sem maiores dificuldades! Beijão!
-
eu resolvi com C12,3 = 220 , mas realmente fiquei pensando em equipeS.
Mas, oque contece é que a Cespe n tem o costume de colocar um valor tão afastado do valor resposta.
Se a questão afirmasse que o resultado seria menor que 250, por exemplo, acho q quase todos nós erraríamos. pq no meu entendimento a questão quis saber C12,3 * C9,3 * C6,3 * C3,3 , como alguns colegas ja mostraram nos comentários acima.
Alfartanos, força!
-
Galera, vou tentar contribuir:
temos 4 equipes, portanto devemos fazer o cálculo para todas elas. O procedimento é o seguinte:
1° equipe: temos 12 agentes para 3 vagas : 12!/3!9! = 110
Temos a primeira equipe!!, porém ainda falta as outras, só que agora temos apenas 9 agentes já que 3 estão na primeira equipe
2° equipe: 9 agentes para 3 vagas: 9!/3!6! = 84
agora nos resta apenas 6 agentes para 3 vagas
3° equipe: 6!/3!3!= 20
Já podemos parar por aqui, pois a questão afirma que há mais de 200 maneiras para se formar as equipes, e podemos provar isso só com as 3 primeiras equipes ( 110 + 84 + 20 = 214)
na última equipe temos 3 agentes para 3 vagas, portanto há uma possibilidade, totalizando assim: 215 formas de montar as equipes
-
Como se diz lá na terrinha, uma coisa é uma coisa, outra coisa é outra coisa.
A matemática já foi muito bem esclarecida pelos colegas.
Essa questão se refere à escolha da primeira equipe, contando com a quantidade de agentes total, apenas.
Para entender melhor o contraste, imagine que fossem 3 equipes nação da Q307256 situa ao invés de 4: O total de combinações de agentes nas 3 equipes possíveis seria C(12,3)xC(9,3)xC(6,3).
-
resolvi da seguinte forma: combinação de 12 três a tres. só fazer o fatorial de 12até o número de vezes que a questão está pedido, ou seja, tres grupos. sendo assim, 12 fatorial:12*11*10:1320. esse valor deve ser dividido pelo número de grupos, pois como se trata de pessoas, a ordem do grupo não irá fazer diferença entre os grupos. ex: A,B,C é a mesma coisa de CAB. nesse sentido, faz-se necessário dividir o resultado pelo fatorial da quantidade de grupos, pois só assim evitará que o mesmo grupo seja contado tres vezes. resposta: 1320/ fatorial de 3: 1320/3*2: 1320/6: 220. conforme gabarito. a questão está correta. há.... ja estava esquecendo, vale passar o bizú. toda vez que for combincAO, deve fazer divisAO para que ocorra uma correcAO. bizú: tudo com ÃO. abraço e sucesso.
-
Na verdade e combinação de uma equipe só, pois, filosofando, a unidade policial poderia querer formar apenas duas equipes. E a plena verdade
-
Como a ordem não importa, podemos resolver por
combinação simples, assim:
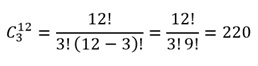
Logo, a quantidade de maneiras diferentes de se
formar essas equipes será superior a 200.
RESPOSTA: CERTO
-
Se a primeira combinação das equipes em 3 agentes, já sugere 220 formas, não há que se calcular mais nada, uma vez que já atingiram a possibilidade mínima do gabarito...Ora, C12,3 = 220 maneiras diferentes de formar equipes de três agentes cada.
-
GABARITO: CERTO
Para formar uma equipe o agente não pode ser repetido e a ordem de escolha desse agente não faz diferença na composição da equipe, logo a conta é de combinação e fica: Cn,p = n! / p! x (n - p)!
C12,3 = 12! / 3!x9! = 12x11x10 / 3x2x1 = 1320 / 6 = 220 equipes.
Prof. Daniel Lustosa - Alfacon
-
C12,3 12 !
-----------------------------------------------
3! (12-3)
12!
---------------------------------------------------
3! 9!
12,11,10,
-------------------------------------------------
3,2,1 12/3 = 4 10 /2 = 5 4X5= 20 20X11 = 220
EXISTEM 220 POSSIBILIDADES
-
Pessoal, acredito estar pedindo a questão as maneiras distintas de se formar CADA EQUIPE, logo seria cada equipe isoladamente. O que traz como resposta 220 possibilidades. Além disso, a banca CESPE, normalmente, oferece alternativas bem próximas do resultado real da questão.
DICA: Se seu resultado for muito diferente do que a questão oferece como alternativa, provavelmente, sua resposta está errada.
Uma opinião pessoal. Abraço e bons estudos!!
-
Galera, também concordo com o RWerneck.
Bons estudos a todos.
-
Pessoal combinaçao simples gente , nao fiquem lokiando do nada so faz assim
C 12,3 pronto ....vc desenvolve de boa o resultado da 220. O pessoal esta viajando , a questao é bem clara no que ela pede , a partir de 12 agentes quantas equipes voce pode formar ..... é so isso gente nao enrolem demais
-
Ao contrário de alguns colegas, como em todas as questões da CESPE, essa merece um pouco de atenção e interpretação, vejamos o que se pede:
C!12,3, logo, pode-se usar o seguinte caminho, que no momento da prova poderá ajudar:
12x11x10 / 3x2x1 = 1.320 / 6 = 220
-
12 11 10 / 3 2
4x11x5 = 220
-
Foi dito:'' maneiras diferentes de se formar essas equipes'', ou seja, 3 agentes em cada equipe das 4.
369600.
-
C= 12*11*10 = 1320 / 6 = 220
gabarito = correto
-
Gab C
C12/3 = 12 x 11 x 10= simplificando = 4 x 11 x 5 = 220
3 x 2 x1
-
Bom pessoal, espero poder contribuir no tocante a parte de ''equipeS''[PLURAL, EQUIPESSSSS]
Podemos observar que no próprio texto que temos uma equipe para cada atividade: SINALIZAÇÃO; EXCESSO DE VELOCIDADE; ULTRAPASSAGENS; e CONDUÇÃO DE VEÍCULO (4 equipes).
Então o que poderíamos fazer é calcular as combinações para cada uma delas:
1a: C(12,3)
2a: C(9,3)
3a: C(6,3)
4a: C(3,3)
Resultando em [C12,3 * C9,3 * C6,3 * C3,3] => 369.600
Podendo ser usado na outra questão. Creio que faltou um pouco mais de clareza, mas vida que segue. A resposta seria Certa mesmo.
-
a partir dos 12 agentes da unidade,Se cada equipe for formada por 3 agentes, então, a quantidade de maneiras diferentes de se formar essas equipes será superior a 200. leiam assim
-
C12,3 = 12X11X10/3X2X1
= 2X11X10(SIMPLIFICANDO)
=220
220>200
-
Acredito que a questão queria os dados de apenas uma equipe, resultando sim em 220, como afirmado comentário do professor e de outros colegas.
Isso ficou mais claro quando olhei a próxima questão dessa mesma prova que pedia:
"Existem 12!/(3!)^4 maneiras de se montar quatro equipes, cada uma delas com 3 agentes."
Isso sim resultaria no cálculo:
C12,3 x C9,3 x C6,3 x C3,3
12!/(3! . 9!) x 9!/(3! . 6!) x 6!/(3! . 3!) x 3!/(3! . 0!)
Simplificando (observe a simplificação pelas cores) ficamos com (apenas a parte em preto):
12!/(3!) x 1 /(3!) x 1/(3!) x 1/(3! . 0!)
Como 0!=1 e ainda agrupando os dados ficamos com:
12!/(3!)^4
Lembrando que a potência 4 é o número de vezes que o 3! aparece no cálculo.
Espero ter ajudado!
-
Depois de olhar esse comentários, fiquei foi com medo. Dica rapaziada: escrevam '' análise combinatória '', ali no campo de busca, e assistam às aulas. Tudo ficará mais fácil. Até de entender como o pessoal está postando loucura aqui (pelo menos a maioria).
-
C 12,3 = 220
-
SERIA UMA COMBINAÇÃO ,
C³12= 12.11.10= 220
---------3.2.1-----
GAB: CERTO
-
Combinação Simples
C=(12,3)=(12x11x10)=1320
3x2x1
1320/6=220
Certa
-
Resolvo essa questão aqui nesse vídeo
https://youtu.be/FxJVNsE36wQ
Ou procure por "Professor em Casa - Felipe Cardoso" no YouTube =D
-
Combinação; função igual.
C12,3: 12.11.10/3.2.1......cortando os números fica 11.5.4= 220
-
Depois d ler os comentários, percebi que a questão dá margem parta duas interpretações: que uma equipe irá orientar para tudo aquilo ou que várias equipes podem ficar responsáveis por cada orientação.
-
GAB: CERTO!
220 possibilidades, feita utilizando a combinação simples!
#CARREIRASPOLICIAIS
-
CERTO.
COMBINAÇÃO SIMPLES.
C12,3 = 220 possibilidades
-
CERTO.
Combinação (C) de 12 e 3.
Resolvendo...
C 12,3 = (12 x 11 x 10) = 1320 | (3 x 2 x 1) = 6
1320 / 6 = 220.