-
Fiz assim: multipliquei o resultado das combinações de mulheres (CM) com o resultado da combinação de homens (CH): CM x CH
A CM é composta por 3 combinações multiplicadas (cada uma representa uma equipe). Na primeira equipe, temos C(15,5), calculada por 15! / (5!10!); na segunda, tem-se C(10,5) = 10! / (5!5!) = 10! / (5!)2; na terceira, C(5,5) = 1.
A CH, da mesma forma, é dada pela multiplicação de 3 combinações, onde os homens ocupam as vagas restantes em cada equipe, ou seja, 15, 10 e 10 vagas. Assim, tem-se: C(35,15) = 35! / (15!20!); C(20,10) = 20! / (10!10!) = 20! / (10!)2; e C(10,10) = 1.
Fazendo CM x CH, temos:
15! / (5!10!) x 10! / (5!)2 x 35! / (15!20!) x 20! / (10!)2 = 35! / [(10!)2 x (5!)3].
Ou seja, sobrou um 5! ali...
Alguém...?
Abraços.
-
Também cheguei na mesma resposta dos colegas acima. Fica sobrando um 5!
-
Que mistério! o mesmo aqui... vou tentar tirar a dúvida com um prof. e posto aqui
-
Também fiquei com um 5! sobrando e acabei errando a questão.
-
Ué! compartilho da dúvida dos colegas! sigo sem saber o pq não da resposta ser (35!) / (10!)2 x (5!)3. Quem puder ajudar, seja bem vindo.
-
Olhando no site da Cespe, ta como certa mesmo, questão 60 da referida prova, ou a gente da comendo bola, ou ninguém entrou com um recurso bom HAUHUA.
Sem querer ser reptitivo, mas aqui também sobrou o 5! ...
Vou refazer essas contas aqui.
-
Fiz assim e acertei de primeira, galera. O pensamento é similar a outra questão da mesma prova. A resolução só muda um pouco pois existem outras variáveis de contorno.
Primeiro, vamos tirar a equipe do PA:
C(35,15) * C(15,5) - Temos um espaço amostral de 35 homens e iremos selecionar 15 deles. Similarmente, temos 15 mulheres e iremos selecionar 5.
Iremos multiplicar isto pelo cálculo para o AM:
C(20,10) * C(10,5) - Temos agora um espaço restante de 20 homens e precisamos selecionar 10 deles. E para as mulheres, restam 10 e iremos selecionar 5.
E para RO:
C(10,10) * C(5,5) - Pensamento similar. E no caso, este produto dá 1.
Multiplicando a parada toda, temos:
[35! / (20! * 15!)] * [15! / (10! * 5!)] * [20! / (10! * 10!)] * [10! / (5! * 5!)] = 35! / [ (10!)^2 * (5!)^2]
Confiram ai, corta numerador com denominador e dá a resposta correta.
-
Colega Leonardo Coelho, resolvi a questão como sugeriu, mas, ainda assim, resultou um 5 a mais.
Alguém conseguiu obter a resposta?
Obrigada pela explicação, foi boa!
-
Ola a todos!
Fiz o calculo porem no meu faltaram 10!
rsssss vou explicar o meu raciocinio.
São pedidas 3 equipes.
Equipe Pará com 20 pessoas.
Equipe Amazonas 15 pessoas.
Equipe Rondônia 15 pessoas.
Sendo que como condição temos que ter 5 mulheres em cada equipe. Irei expressar os sexos com H --> homem e M --> mulher.
Calculo da equipe Pará:
C15,5(M) x C35,15(H)
15! / 5! 10! x 35! / 10! 20!
Calculo da equipe Amazonas:
C10,5 (M) x C 20,10 (H)
10! / 5! 5! x 20! / 10! 10!
Calculo da equipe Rondônia: (notem q sobraram somente 5 mulheres e 10 homens para compor a ultima equipe. sendo assim como o numero de pessoas é igual ao numero de vagas adotei permutação)
P 5! (M) P10! (H)
Multiplicando todas equipes teremos:
(10!/5! 10!)x(35!/15!20!)x(10!/5!5!)x(20!/10!10!) x 5! x 10!
Simplificando a equação teremos:
35! / (5!)2 10!
No meu caso faltou um 10!
-
Q questão encapetada é essa? se alguém souber de anulação ou resolução que tenha dado o resultaado, favor informar. O meu também sobrou um 5!....
-
Opa! Perdão galera, eu prometi tirar a dúvida e postar aqui...
Pedi para o meu professor, o Antônio Geraldo resolver e ele encontrou o mesmo resultado que nós encontramos.
Será que não foi um erro na transcrição do item??
-
Mais uma questão vergonha do CESPE :( .. como que não anularam isso? .. (sobrou um 5! aqui também)
-
A transcrição da questão está OK, já conferi.. e aqui sobrou um 5! tb..
-
Desconsiderando as mulheres, já que elas somam 15 e necessariamente cada equipe vai ter 5 mulheres, vamos fazer a combinação apenas com os homens e multiplicar pela permutação das mulheres (5! para cada equipe).
Uma equipe tem 20 vagas, tendo necessariamente 5 vagas pra mulheres e, consequentemente, 15 vagas pra homens:
C35,15 → 35 homens para 15 vagas
Como 15 vagas já foram preenchidas por homens (sobram 20 homens), a próxima equipe, que terá 15 pessoas, conterá 5 mulheres e 10 homens:
C20,10 → 20 homens para 10 vagas
Como 10 vagas já foram preenchidas por homens (sobram 10 homens), a próxima equipe, que terá 15 pessoas, conterá 5 mulheres, e 10 homens:
C10,10 → 10 homens para 10 vagas

Eu vi que na resolução de vocês sobrou um 5!, mas nos meus cálculos sobrou um 15! também...
Muito estranho esse gabarito...
-
Será que não vai aparecer um fí de Deus pra nos dizer de onde ta aparecendo esse 5!? ou onde foi que o ezaminador do CESPE enfiou esse bendito 5!? Já refiz essa questão trocentas vezes e só da
35!
--------------------------------------------
(10!) x (10!) x (5!) x (5!) x (5!)
-
O professor Brunno Lima do EVP corrigiu essa prova e afirmou ser IMPOSSíVEL essa questão estar certa.
-
Esse CESPE abusa mesmo, erra feio e nem para corrigir a resposta. Não é a primeira e nem vai ser a última vez que eles vão fazer isso. ABSURDO!
-
oO Sobrou um 5! aqui tb.
Prof. Bruno Lima do EVP resolveu a questão e a reposta dele foi a mesma: 35!/ 5!³ 10!²
-
Poxa, sobrou um 5! perdido aí, no meio do negócio... Errada a questão...
-
Realmente, ficou sobrando um 5!
-
Temos um total de 15 mulheres e 35 homens e deve-se garantir exatamente 5 mulheres em cada equipe de acordo com o enunciado.
Logo, as equipes enviadas para os estados do Pará, Amazonas e Rondônia (descontando as 5 mulheres), terão um total de 15, 10 e 10 homens respectivamente. Assim, começando pelo estado do Pará:
20 fiscais no total (15 homens e 5 mulheres). Escolhendo 15 homens e 5 mulheres dentre o grupo de 35 homens e 15 mulheres, aplicaremos uma combinação simples (pois não importa a ordem dos fiscais na equipe), lembrando que teremos que separa o conjunto das mulheres do conjunto dos homens:
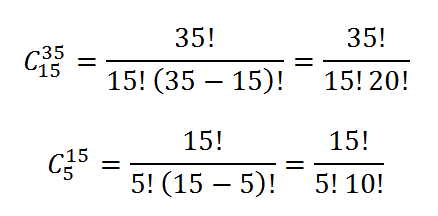
Multiplicando os resultados acima (pois devemos ter homens E mulheres no grupo):
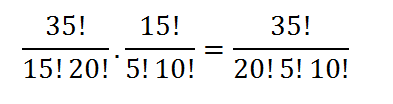
Seguindo o mesmo raciocínio para a seleção nos outros estados:
Amazonas: 15 fiscais (10 homens e 5 mulheres), num total restante de 20 homens e 10 mulheres:
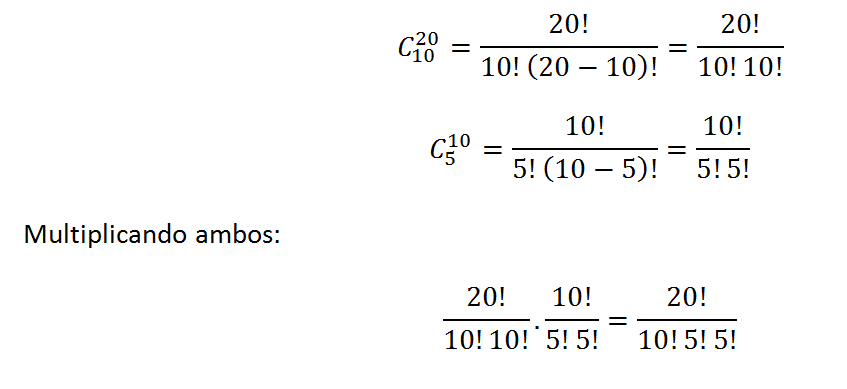
E no último estado de Rondônia, formada com 10 homens e 5 mulheres restantes, teremos apenas 1 maneira de montar essa equipe. Assim:
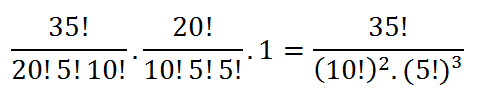
O que difere da banca, logo o resultado correto seria ERRADO e não CERTO como aponta a banca.
Gabarito da Banca: Certo
Gabarito do Professor: Errado.
-
Equipe A C15,5 . 35,15
Equipe B 10,5 . 20,10
Equipe C 5,5 . 10,10
-
cespe não anulou... e manteve como certa... afff
-
Simples. Quem "acerta" essa questão fez errado.
-
Cespe não alterou o gabarito, pessoal. Só isso. Realmente sobra 5! ali no denominador, portanto o item é ERRADO. Mas, a banca deu o gabarito como certo. Não sei se teve recurso na época desse concurso, mas como a banca manteve o gabarito, imagino que se teve foi indeferido e não apresentaram uma justificativa plausível. Infelizmente, algumas questões de concursos anteriores da banca sofrem disso.
Bons estudos.
-
E depois de vários anos, o professor Carlos Henrique resolveu e deu errada também. Sobrou um 5!
-
Galera, no material que adquiri a questão está errada... Resolvendo ficaria 5! ao cubo, como comentado pelos colegas.
-
Se você errou, então acertou. Fique tranquilo
-
Grupo Pará = C15,5 x C35,15
Grupo Amazonas = C10,5 x C20,10
Grupo Rondônia = C5,5 x C10,10
Após jogar na fórmula da combinação, você vai cortar tudo aquilo que é semelhante (o corte é entre o denominador e o numerador). Ao final, sobrarão 35! / (5!)^3 x (10!)^2
questão FLAGRANTEMENTE ERRADA! pois faltou mais um 5! no denominador
-
https://www.youtube.com/watch?v=7O2xNWIFpbs
-
Apesar dos apesares do gabarito. Foi uma questão legal de se desenvolver.
-
PARA QUEM NÃO SABE:
ESSA DAQUI É A SEGUNDA MAIOR FRAUDE QUE JÁ OCORREU NOS MUNDOS CONCURSOS!
"qual a primeira?"
não conto.