-
M=20, F=40, Q=30, MeF=10, MeQ=5, QeF=15
MouFouQ = M + F + Q - MeF - MeQ - QeF +MeFeQ
MouFouQ = 75 - 10 = 65
65 = 20 + 40 + 30 - 10 - 5 - 15 + MeFeQ
MeFeQ = 5
SóMeQ = MeQ - MeFeQ
SóMeQ = 5 - 5 = 0
Letra A
até mais!
;)
-
Se alguém conseguiu fazer usando o diagrama de Venn, poderia demonstrar? Obrigada!
-
Faltou a questão por a informação de quantos alunos gostam das 3 disciplinas, pois sem ela não da pra fazer a questão.... No meu caso eu chutei como 5 e após todas as interseções vi que "5" era exatamente o número de alunos que gostam das 3 matérias e só sabendo este número que você terá meios pra solucionar a questão.... Brigado ;)
-
Pessoal,
Segue a resolução passo a passo no link abaixo. Espero que ajude!!!
http://imageshack.com/a/img713/636/4yjx.jpg
Bons estudos!
-
Gente, li os comentários acompanhada consigo fazer essa questão, mas quando tento outras parecidas complica tudo, os 5-5, alguém pode me ajudar?
-
Bem sacana essa questão, pois ela não afirma que existem alunos que gostam de 3 matérias ao mesmo tempo, no entanto, ela também não afirma que NÃO existem alunos que gostam de três matérias simultaneamente.
-
O enunciado não cita que existem alunos que
gostam das 3 disciplinas, mas também não faz menção alguma dizendo que não
existem, logo, iremos assumir que existem. Fazendo o diagrama de Venn Abaixo:
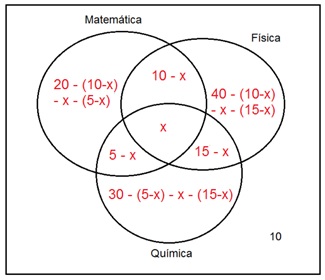
Assim
temos:
M
= 20 – (10 - x) – x – (5 - x) = 20 – 10 + x – x – 5 + x = x + 5
F = 40 – (10 - x) – x – (15 - x)
= 40 - 10 + x – x - 15 + x = x + 15
Q = 30 – (5 - x) – x – (15 - x) =
30 - 5 + x - x - 15 + x = x = x + 10
Somando tudo e igualando ao total de
alunos menos os que não gostam de nenhuma disciplina, ou seja, 75 – 10 = 65:
(M)
+ (F) +(Q) + (M + F) + (M + Q) + (F + Q) + (M + F + Q) = 65
=
(x + 5) + (x + 15) + (x + 10) + (5 – x) + (15 – x) + (10 – x) + x = 65
x +
60 = 65
x =
65 – 60
x =
5
Logo a quantidade de alunos que gostam somente de
Matemática e Química é (5 – x) = (5 – 5) = 0.
RESPOSTA: (A)
-
Não é necessário saber a interseção dos três: chame de x.
Assim, o número de alunos que gostam somente de química e matemática fica 5-x;
O número de alunos que gostam somente de química e física fica 15-x;
O número de alunos que gostam somente de matemática e física fica 10-x;
Os que gostam somente de matemática são m = 20-(10-x)-(5-x)-x => m=x+5
Os que gostam somente de física são f = 40-(10-x)-(15-x)-x => f=x+15
Os que gostam somente de química são q = 30-(5-x)-(15-x)-x => q=x+10
Coloque tudo isso num diagrama de venn e ponha o número 10 do lado de fora, i.e., os que não gostam de nenhuma das matérias. Somando todos os elementos, teremos 75, que é o total de alunos. Assim:
x+(5-x)+(15-x)+(10-x)+(x+5)+(x+15)+(x+10)+10 = 75
x=5
Os que gostam somente de matemática e química são (x-5). Portanto, x-5 = 5-5 = 0.
Gabarito A
-
Aos que tentaram explicar, me desculpe, mas ainda não entendi pq a resposta é zero, se pelo diagrama que eu fiz, deu que somente matemática são 5 e somente quimica são 10.
-
Daniela Matos, a questão não pergunta quantos gostam somente de matemática e somente de química. Ela pergunta quantos gostam somente de matemática e química, ou seja, pede a interseção dessas duas matérias.
-
Resposta A
----------------------------------------------------
A- Qual o número de alunos que gostam somente de matemática? 8 alunos
B- Qual o número de alunos que gostam somente de física e química? 18 física 13 química
C- Qual o número de alunos que gostam de pelo ao menos uma das três disciplinas? 63 alunos
D- Qual o número de alunos que não gostam de nenhuma das disciplinas citadas? 12 alunos
Importante "...pois ela não afirma que existem alunos que gostam de 3 matérias ao mesmo tempo" WagnerdosSantos
https://goo.gl/Mp99dT
#sefazal
-
Essa aí e difícil de mais
-
Não consigo entender a diferença entre "somente matemática e química" e "matemática e química"
Porque SóMeQ = MeQ - MeFeQ?