-
Prezados, o drama é o seguinte:
50 vagas para 48 carros, 48 carros estacionam a vontade (1º carro tem 48 possibilidades de vaga, 2º tem 47 possibilidades de vaga até o 48º carro ter 1 possibilidade de vaga, totalizando 48! possibilidades para todos) e sobram 2 vagas dentre as 50 iniciais (que podem ser quaisquer dentre elas, por isso temos que fazer a combinação de 50 escolhe 2, para pegar o total de vezes que podemos encontrar 2 vagas vazias entre 50 vagas), com isso ficamos com
C50,2 x 48! = 1225 x 48!
A questão diz que temos mais de 1000 x 48!, como 1225 > 1000, pode marcar correto sem medo!
-
Entendi que, a posição onde o carro esta estacionado importa, neste caso a ordem importa (Arranjo). O "posição da vaga" também importa, posso contá-la como um carro estacionado, neste caso tenho 50 vagas para 50 status (carro nº y ou vaga), então temos:
A50,50 = 50!
A50,50 = 50 x 49 x 48!
A50,50 = 2450 x 48!
-
Prezado Diego,
Você deve desprezar o fato de que qualquer arranjo
com as duas vagas não preenchidas (sem carro) são iguais para uma
permutação exclusiva entre elas.
Para compreendermos, vamos
considerar 4 vagas para apenas 2 carros, sendo um carro representado
pela letra A, o outro pela letra B e a vaga não preenchida representada
pelo número 0. Dessa forma, teríamos os seguintes arranjos:
01. AB00
02. A0B0
03. A00B
04. BA00
05. B0A0
06. B00A
07. 0AB0
08. 0A0B
09. 0B0A
10. 0BA0
11. 00AB
12. 00BA
Se o seu pensamento fosse correto, teríamos na verdade 24 arranjos, ou seja, a permutação de 4 elementos:
4! = 4 x 3 x 2 x 1 = 24
Ora, então por que tivemos apenas 12 arranjos possíveis na discriminação dos arranjos possíveis, acima?
Porque
quando temos elementos idênticos em um conjunto, temos de desprezar a
permutação entre eles pois essa permutação não gera um arranjo diferente.
Se ainda não tiver ficado claro, vamos analisar o primeiro arranjo
demonstrado acima.
Se invertemos os dois primeiro elementos do
arranjo AB00, teremos o arranjo BA00, um arranjo diferente, mas o mesmo
não ocorre se invertermos os dois últimos elementos (ambos os elementos
são o zero).
Uma forma de descartar as permutações que não geram
arranjos diferentes é dividir o número de permutações de elementos
distintos pelo número de permutações de elementos idênticos. Trata-se de
uma permutação com elementos repetidos que, no caso do problema, é
resolvido da seguinte forma:
50! / 2! = 25 x 49 x 48! = 1225 x 48!
"Permutação de cinquenta elementos com um deles repetido duas vezes."
-
O primeiro carro dos 48 que entrar no estacionamento poderá escolher qualquer uma das 50 vagas, assim para o primeiro carro existem 50 possibilidades de estacionar. Já o segundo carro que entrar terá 49 possibilidades, o terceiro, 48 possibilidades, o quarto, 47 possibilidades e assim por diante, até o último carro, o 48º entrar, para esse haverá 3 vagas sobrando, ou 3 possibilidades.
Logo, o total de possibilidades é dado por
50 . 49 . 48 . 47. 46. ............ 6 . 5 . 4 . 3.
Não é a afirmação que aparece na questão, porém se analisarmos :
48 ! = 48 . 47. 46. ............ 6 . 5 . 4 . 3 . 2 . 1 poderemos escrever,
50 . 49 . 48 . 47. 46. ............ 6 . 5 . 4 . 3 = 50 . 49 . ( 48!) /2 = 25 . 49 . 48! = 1225 . 48!
Como encontramos 1225 . 48! que é maior que 1000 . 48! A afirmação da questão está CORRETA
Fonte: http://nenecomatematica.blogspot.com.br/
-
Certo!
Essa questão fiz da seguinte forma:
Existem 50 vagas porém só serão utilizadas 48. Desta forma temos uma combinação: C50,48= 50!/48!(50-48)!= 1225 Maneiras de se escolher as vagas.
Agora existem 48 veículos e todos serão utilizados. Temos 48!
Multiplicando a maneira de se escolher as vagas 1225 por 48! (De escolha dos carros) = 1225.48!
-
Nas
primeiras 48 vagas, os carros podem estacionar de acordo com o desenho abaixo:
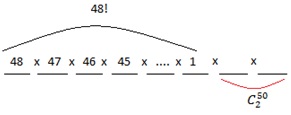
Ou seja,
48!, as duas outras vagas que sobram, podem se situar em qualquer lugar, não
apenas como no desenho acima, elas na verdade podem estar no início, no meio
... assim, temos que fazer uma combinação de 50 para 2, assim, cobrimos toda as
posições que essas duas vagas podem se encontrar dentre as 50.
Temos
48!.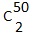 
= 48!.1225 > 48!.1000
A
resposta é “Certo”.
-
Só acrescentando ao comentário abaixo:
C50,48 = C50,2
Encontrar quantas maneiras de ocupar 48 vagas de 50 eh a mesma coisa que encontrar as maneiras de deixar 2 vagas em 50.
-
Mais fácil por arranjo! A(50,48) = 50!/2! = 50 x 49 x 48! / 2 = 2450 x 48! / 2 = 1225 x 48!
-
Finja que tem dois carros fantasmas, então seria 50! / (2*1). essa divisão pq as duas vagas vazias(carros fantasmas) são "iguais", então foram contadas várias vezes(o número de permutações de duas vagas, q é 2*1)
-
MOLE, MOLE, GALERA!!!
* Dados do problema:
. 50 vagas;
. 48 veículos.
* Então, como é que fica?
Você pode trabalhar a relação 50/2 (nº de vagas / vagas que sobram) ou 50/48 (nº de vagas / nº de carros), que dá na mesma,
já que vamos trabalhar com combinação. A ordem não importa.
C(n,p)= n! C(50,2)= 50! C= 50. 49. 48! = C= 25.49 = C= 1.225
p! (n-p)! 2! 48! 2. 48!
Agora, imagine 50 vagas e que cada uma delas receba uma numeração. Ou seja, cada nº representa uma vaga.
| 50 | 49 | 48 | 47 | 46 | 45 | 44 | ... | 01 |
1.225 . 48!
As vagas 50 e 49 (2 vagas, portanto) representam, dentre 50 vagas, 1.225 possibilidades de estacionar 48 carros.
Isso é multiplicado pelo restante das vagas preenchidas com 48 carros.
* GABARITO: CERTO.
(Fiz esse exercício 250 vezes. Errei 251. Mas é assim mesmo: "Todas as coisas são difíceis, até que se tornem fáceis". Mole, Mole!!!)
Abçs.
-
boa questão..
-
a ordem dos veículos vai alterar a permutação, portanto é um arranjo
A (50,48) = 50! / 2!
50 * 49 = 2450
2450 / 2! = 1225
resp. = 1225 * 48!
questão correta
-
1. QUANTOS GRUPOS DIFERENTES CONSIGO FORMAR COM 48 VEICULOS ?
RESPOSTAS: C 50,48 = 1225 GRUPOS/POSSIBILIDADES
2. AGORA QUANTAS POSSIBILIDADES EU TENHO DE EMBARALHAR UM GRUPO, OU SEJA, TROCAR DE POSIÇÃO OS CAROS DENTRO DE APENAS UM GRUPO ?
1 X 48! = ???
AGORA MULTIPLICA TODOS OS GRUPOS DIFERENTES: 1225 X 48!
OBS: PODE TER CERTEZA QUE DA BEM MAIS QUE 1.000 × 48!
-
Alguém sabe me dizer porquê multiplicou o 1225 por 48! ?
-
Acredito que o melhor caminho seja mesmo enxergar tratar o problema como uma permutação com repetição.
De quantas formas pode se ocupar 50 vagas, sendo que 2 delas serão ocupadas do mesmo jeito (ou seja, serão não ocupadas).
P (50,2) = 50! / 2! = 50 * 49 *48! / 2 = 1225 * 48!
-
Para quem ficou sem entender essa questão... segue o link de um video no yt https://www.youtube.com/watch?v=aUffSAVhFJk a partir do 31:50
Tentando resumir
são 50 vagas e 48 carros
carro 1 pode escolher uma vaga entre 50
carro 2 pode escolher uma vaga entre 49
C 3 - 48
C 4 - 47 e assim por diante até o carro 48 poder escolher 3 vagas.
50.49.48.47.46.45 ... 4.3 quase 48! só falta o 2 .
dessa forma, fazemos 25.2 = 50 pegamos esse 2 e jogamos depois do 3, completando assim o 48!
temos então, 25.49. 48.47.46.45...4.3.2, ou seja 48!
25x49x48!
1225x48!
-
Basta fazer o arranjo, gente! Fica mais simples o raciocínio. :) vejam o comentário do Hilano
-
Sempre q ser falar em posição, é arranjo.
-
Galera complica demais. Só realizar por arranjo. Até achei que tinha feito de forma equivocada e acertei "sem querer", Mas por arranjo é a melhor forma.
-
PERMUTA OS 48 VEÍCULOS NAS 48 VAGAS = 48!
COMO SÃO 50 VAGAS TOTAIS, RESTA PERMUTAR OS 48 VEÍCULOS NAS 50 VAGAS (AGORA USANDO AS OUTRAS DUAS)
50! / 48! . 2!
50.49.48! / 48! . 2!
50 . 49 / 2!
2250 / 2 = 1225
-
Só pensar em uma fatoração com repetição. As duas vagas vazias seriam as repetições.
50! / 2! =
(50x49x48!) = 25x49x48! = 1225 x 48!
-
https://www.youtube.com/watch?v=aUffSAVhFJk
Tempo: 31min
-
RESOLUÇÃO DA QUESTÃO:
https://sketchtoy.com/69534716
-
Outra questão da CESPE que ajuda a responder:
Três pessoas entraram em uma sala de cinema onde restavam apenas 5 assentos desocupados. Nesse caso, a quantidade de maneiras diferentes de essas pessoas ocuparem esses assentos é igual a:
Resposta correta: 60
São 3 Pessoas que escolherão entre 5 lugares disponíveis.
A primeira pessoa tem 5 opções para escolher; 5 x
A segunda pessoa tem 4 opções para escolher; 4 x
A terceira pessoa tem 3 opções para escolher; 3 x
5! / 2
5.4.3.2.1 / 2 (Divide o 2 pelo 2)
= 60
---------------------------------------------------------------
No caso desta questão vale o mesmo raciocínio, os carros tem 50! / 2! possibilidades de escolher o estacionamento:
50 x 49 x 48! / 2 (Divide o 50 pelo 2 no denominador)
25 x 49 x 48!
= 1225 x 48!
Ou seja, o valor deu superior a 1000 x 48!, portando questão correta.
-
Olá, pessoal.
Nessa questão devemos usar Arranjo. Para eu saber que um problema deve ser feito usando Arranjo, uso o seguinte pensamento: tenho uma quantidade de elementos que é MAIOR que outra. Nesse caso, temos o elemento vagas( = 50) que é o MAIOR que o elemento carros ( = 48).
ATENÇÂO: se fosse uma Permutação, os elementos seriam iguais.
FÓRMULA DO ARRANJO: T! / (T - t)!
Sendo T: elementos com MAIOR quantidade
t: elementos com menor quantidade
A = 50!/(50-48)!
A = 50!/2!
A = 50.49.48!/2!
A = 25.49.48!
A = 1225.48!
O resultado, portanto, é maior que '1000.48!'.
Gabarito: CERTO
fonte: Estratégia
-
1- Escolha dentre as 50 garagens as 48 que você usará para posicionar os carros:
Como a ordem não importa, usaremos combinação.
C(50,48) = C(50,2) = 50.49/2 = 1225
2- Posicione os carros nas respectivas garagens escolhidas
Como a ordem importa, usaremos permutação
P(48) = 48!
Perceba que eu dividi a questão em 2 passos cumulativos, uma coisa E outra, matematicamente, uma coisa X outra.
48! x 1225
-
Pensa assim o carro nº 1 vai ter 50 opções
o carro nº 2 vai ter 49
e assim por diante...
Até que o último carro vai ter 3 opções e vão sobrar 2 vagas.
Isso parece como o quê? Isso é exatamente 50!/2!
Então você faz (50*49*48!)/2! = 25*49*48!
E fazendo a conta 25*49 = 1225 que é maior que mil
Logo, a quantidade de opções que se tem é:
1225*48!
-
A conta é simples:
Número de vagas total: 50
Número de vagas que ficarão vazias: 2
Logo: 50!/ 2! = 50 x 49x 48..../2 = 1225 x 48!
Logo é maior que 1000 x 48!
Gabarito: certo