-
Gabarito: letra A
Este é um exercicío de grandezas diretamente e inversamente proporcionais. Lendo-o vc irá perceber que se trata das duas modalidades na mesma questão, o que exige um pouco mais de atenção. Quase sempre (ou pelo menos eu nunca vi diferente) esse tipo de questão resultará num sistema linear com 2 ou 3 equações, veja:
Dados:
Vendedor A ----- 6 anos e 5 faltas
Vendedor B ----- 4 anos e 3 faltas
Para dividir a quantia é necessário introduzir uma razão R, que é o fator determinante para dar prosseguimento ao exercício.
A e B representam as quantias que irão receber:
A = 6 X R / 5 ( a multiplicação significa a proporcionalidade direta e a divisão a proporcionalidade inversa )
B = 4 x R / 3 ( a mesma coisa )
A + B = 2.166 ( significa a quantia total distribuida entre os dois vendedores )
Agora é só substituir as 2 equações acima na terceira e encontrar a Razão. Com esta razão descobre-se os valores recebidos e finaliza-se a questão. R = 855, A= 1026, B= 1140.
A - B = 114
Bons Estudos!
-
Quanto mais tempo de trabalho mais bônus (diretamente proporcional): x/y=4/6
Quanto mais faltas menos bônus (inversamente proporcional): x/y=5/3
Assim temos:
X = 4 . 5
Y 6. 3
X = 20
Y 18
18X = 20Y
Y=18X
20
X + Y = 2166
X + 18X = 2166
20
X = 1140
Y=18X = 18 . 1140 = 1026
20 20
1140 - 1026 = 114
-
Aproveitando excelente comentário do colega Fernando, mas finalizando de uma forma mais simples.
Temos:
X = 4 . 5
Y 6. 3
X = 20
Y 18
18X = 20Y
Sabemos que temos 18 partes para X e 20 partes para Y, totalizando 38 partes. Dividindo o total (2.166) por 38, teremos:
=> 2.166 / 38 = 57. A questão pede apenas a diferença de valores entre X e Y. Temos que a diferença é de apenas duas partes (20 de Y menos 18 de X). Cada parte vale 57. 57 x 2 = 114. Alternativa "A"!
-
Vamos
montar um sistema com as seguintes equações:
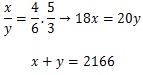
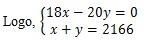
Resolvendo
o sistema acima acharemos x = 1140 e y = 1026, assim, 1140 - 1026 = 114.
Letra A.
-
gabarito A, o colega abaixo deu o jeito amais fácil de se resolver esse tipo de questão!achando as frações correspondentes de x e y depois somam-se essas frações, que serão o todo, esse "todo" dividirá a quantidade que se quer, pra se achar uma parte, depois se multiplica pelas respectivas frações de x e Y.
RESUMINDO: 1 acha-se as frações; 6x/4y * 3x/5y(nota-se que inverteu nessa), isso vai dar:18/20; simplificando 9x/10y.
resumindo:2= se tem 9 partes de x, e 10 de y; logo tem-se 19 em 2166 reais, agora procura-se uma parte,2166/19; dará 114 reais; agora se é 9x será 9 * 114=1026; se é 10y ,10 * 114= 1140; a diferença entre eles é 114 reais, que coincidentemente é o valor de uma parcela, a qual um tem menos que o outro
-
2166/ (1/5 x 6 + 1/3 x 4)= 855
855 x 1/5 x 6= 1026
855 x 1/3 x 4= 1140
1140-1026= 114
gabarito A
achei essa forma mais simples e rápida das aqui sugeridas..
-
Acredito que esteja havendo um erro na montagem das equações, mas que não altera o resultado.
Diferente do dito aqui, a proporcionalidade direta é expressa pela divisão e a indireta pela multiplicação!
Sendo assim, considerando X e Y os dois vendedores nesta ordem, teríamos a seguinte expressão:
5X/6 = 3Y/4 = k (constante) ===> X = 6k/5 e Y = 4k/3.
Sabendo que X + Y = 2166, temos 6k/5 + 4k/3 = 2166, que resolvendo teríamos k=855.
Substituindo k em X e Y, teríamos X = 1026 e Y = 1140. A diferença é a mesma, mas o primeiro vendedor receberia R$1026 e o segundo R$1140.