-
Falta uma informaçao nesta questão:
(copiado da colega Rayanne)
A respeito das auditorias realizadas pelos auditores A1, A2 e A3 de
um tribunal de contas, concluiu-se que:
• A1 realizou 70 auditorias;
• A3 realizou 75 auditorias;
• A1 e A3 realizaram, juntos, 55 auditorias;
• A2 e A3 realizaram, juntos, 30 auditorias;
• A1 e A2 realizaram, juntos, 20 auditorias;
• das auditorias que não foram realizadas por A1, somente
18 foram realizadas por A2;
• A1, A2 e A3 realizaram, juntos, 15 auditorias.
fonte: http://www.cespe.unb.br/concursos/TCE_RO_13/ (caderno de prova - conhecimentos basicos - cargo 8)
-
Colegas,
Alguém pode comentar? O meu resultado deu 10 auditorias realizadas apenas por A3!
Abraços!
-
mesmo faltando a informação dá pra responder! Os três realizaram juntos 15 auditorias! Então, subtraia 15 dos seguintes: A1 e A3 realizaram, juntos, 55 auditorias ; • A2 e A3 realizaram, juntos, 30 auditorias; • A1 e A2 realizaram, juntos, 20 auditorias; Ficam 40, 15 e 5! faça os desenhos das interseções Euller! Ai vc soma 40 (1 e 3), 15 (2 e 3), 15 (1, 2 e 3) que dá 70. A questão afirma que • A3 realizou 75 auditorias; então, ele sozinho realizou 5 auditorias!
-
Complementando...
É meio confuso no início, mas é só não achar q, nesse caso, uma auditoria feita por A1 e A2, não foi feita por A3, tbm. A não ser q a afirmativa seja "somente por A1 e A2".
Somente "só, somente, unicamente, etc.", restringem casos!!!
"Si vis pacem parabellum"
-
Só para lembrar o que o amigo André falou - Faltam informações no corpo da questão, sem as quais não seia possível o seu entendimento e solução.
O fato de A1 ter realizado um total de 70 auditorias.
É importante mencionar também que eu demorei a entender que auditorias somadas, ou seja, feitas por mais de um auditor, se tratam de uma interseção
no conjunto de auditorias.
Exemplo: A1 + a2 + A3 = 15 --> É a interseção dos três conjuntos de auditorias (são auditorias feitas pelos tr~es auditores ao mesmo tempo)
Não sei se por estar muito tempo sem estudar, mas eu edemorei a entender issso. Num primeiro momento eu estava interpretando como:
A1 U A2 U A3 e não da forma correta que deveria interpretar, ou seja, a interseção dos três conjuntos A1, A2 e A3.
Esse entendimento é a base para solucionar essa questão.
Espero ter ajudado.
-
Caraca, não consegui entender até agora!!!!
-
Fernando, vou tentar ajudá-lo:
Faça três conjuntos, onde A1, A2 e A3 formem interseções. Agora comece a preencher os conjuntos a partir da última informação ( A1, A2 e A3 realizaram, juntos,15 auditorias), daí continue preenchendo com as demais informações e chegará no resultado.
Bons estudos!
-
A respeito das auditorias realizadas pelos auditores A1, A2 e A3 de um tribunal de contas, concluiu-se que:
• A1 realizou 70 auditorias;
• A3 realizou 75 auditorias;
• A1 e A3 realizaram, juntos, 55 auditorias;
• A2 e A3 realizaram, juntos, 30 auditorias;
• A1 e A2 realizaram, juntos, 20 auditorias;
• A1, A2 e A3 realizaram, juntos, 15 auditorias.
Comece de baixo pra cima:
• A1, A2 e A3 realizaram, juntos, 15 auditorias.
• A1 e A2 realizaram, juntos, 20 auditorias (5 pra cada um, pois já temos 15 para os três juntos)
• A2 e A3 realizaram, juntos, 30 auditorias (15 pra cada um, pois já temos 15 para os três juntos)
• A1 e A3 realizaram, juntos, 55 auditorias (40 pra cada um, pois já temos 15 para os três juntos)
• A3 realizou 75 auditorias (75 - 15¹ - 15² - 40³ = 5), logo, A3 resolveu, sozinho, 5 auditorias!
1 = A3 figura em 15 auditorias trabalhando os três juntos;
2 = A3 figura em 15 auditorias trabalhando com A2;
3 = A3 figura em 40 auditorias trabalhando com A1.
Galera, resposta correta, mas faça isso nos diagramas de Venn.
-
Comece pelo 15 da intercessao dos 3 conjuntos. Ou seja, 15 processos trabalhados por 3 pessoas juntas, são 3 pessoas trabalhando em um processo, depois 3 trabalhando em outro, até 15...
Depois repare que o comando diz que A1 e A3 estiveram trabalhando juntos em 55 processos, mas não vá marcar 55 direto na intercessão entre de A1 e A3. Não deixe de considerar que você já posicionou, no diagrama, 15 processos em que A1 e A3 estiveram trabalhando juntos, embora contassem com A2. Ao preencher a intercessão entre A1 e A3 voce estará representando a quantidade de processos trabalhados pelo auditor A1 com a ajuda de A3, sem a presença do A2.
-
Pelo
diagrama de Venn:
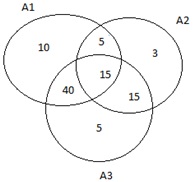
Vemos que
realmente 5 auditorias foram realizadas pelo auditor A3.
Certo.
-
Desenhe o diagrama com três conjuntos e vá montando com os seguintes valores:
a interseção entre os 3 conjuntos é: 15
vamos começar os cálculos:
A1 fez no total 70 auditorias, mas quantas ele fez sozinho?
A3 fez no total 75, mas quantas fez sozinho?
veja, A1 +A3 = 55, então 55 - 15 = 40 é a interseção entre A1 e A3.
ainda, A2 + A3 = 30, então 30 - 15 = 15 é a interseção entre A2 e A3.
e por último, A1 + A2 = 20, então 20 - 15 = 05 é a interseção entre A1 e A2.
Agora faz os cálculos para saber quanto cada um fez sozinho:
A1: 70 - (40+15+5) = 10
A3: 75 - (40 + 15 + 15) = 05
A2: a questão diz que das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2, então: 18-15 = 03
-
Ó céus, porque não nasci sabendo jogar bola?!
-
Ia perder essa questão por falta de atenção.Quase vacilo!Quase!
-
só uma pergunta, se eu quisesse saber o numero de auditoria feitas somente por A2, teria como responder ?
-
Hn Silva,
• A2 e A3 realizaram, juntos, 30 auditorias. Subitrai-se a interseção que é 15, você terá 15
• das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2
Logo, 18-15 = 3 ( que realizaram apenas A2).
-
A1`10
A2: 3
A3: 5
-
GABARITO CERTO
O ideal nesse tipo de questão é começar pela intersecção dos três conjuntos:
A1 ^ A2 ^ A3 = 15 auditorias
A1 ^ A2 = 20 - 15 = 5 auditorias
A1 ^ A3 = 55 - 15 = 40 auditorias
A2 ^ A3 = 30 - 15 = 15 auditorias
A1 = 70 - 40 - 15 - 5 = 10 auditorias
A3 = 75 - 40 - 15 - 5 = 5 auditorias
A2 = das auditorias que não foram realizadas por A1 (20 auditorias), somente 18 foram realizadas por A2. Como A2 já conta com 15 auditorias realizadas em comum com A1, logo A2 realizou somente 3 auditorias.
-
Acredito que essa seja a dúvida da maioria:
Quando fala que "das auditorias que não foram realizadas por A1, somente 18 foram realizadas por A2" significa que quando as bolinhas já estiverem preenchidas, você 'separa o A1, e o restante do A2 deve toalizar 18. Mas como já temos 15 da interseção SOMENTE A2 com A3, resta 3 para o SOMENTE A2.
Sacou??
-
Saquei, tks., Dani Cruz
-
Uma sequência de questões como essa na PCDF seria o ideal kkk
-
Gaba: CERTO
fiz um vídeo que explica como achar o A2
https://youtu.be/JVXP2exL82Y
bons estudos.
-
Minha contribuição.
Diagramas de Venn
A1, A2, A3 = 15
A1,A2 = 5
A1,A3 = 40
A1 = 10
A2,A3 =15
A2 = 3
A3=5
Total: 93
Abraço!!!