-
Não entendi porque 15
-
Para cada dupla de atividades, há apenas um funcionário. Logo, se acharmos quantas possibilidades de duplas existem, também teremos a solução.
Enfim, basta calcular combinação 6-2, que dará 15, o gabarito da questão.
-
C(6,2) = 6! / 2.(6-2)! = 6x5x4! / 2x4! = 30/2 = 15
-
Sinceramente, não entendi pq utilizar combinação.
Se eu tenho 6 atividades: a, b, c, d, e, f.
O funcionário 1 poderia executar: a, b.
o 2: c, d.
o 3: e, f.
Pq precisaria de mais? Como esta situação estaria em desacordo com o enunciado?
(Agradeço quem puder responder).
-
Para resolução de questões de combinação usa-se a fórmula C(Grupos,elementos),
exemplo 1==> C(3,3) = 3x2x1 / 3 = 2
exemplo 2 ==> C(5,3) = 5x4x3 / 3 = 20
exemplo 3 ==> c(4,4) = 4x3x2x1 / 4 = 6
exemplo 2 ==> C(5,4) = 5x4x3x2 / 4 = 30
Nesta questão as pessoas são os grupos e as tarefas são os elementos, então:
C(6,2) = 6x5 / 2 = 15
-
De acordo com o enunciado, temos uma combinação tomados de 6 a 2, assim:
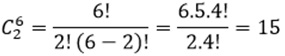
Letra C.
-
Vandré, essa é uma das possibilidades, a questão pede quantas são..
São 6 atividades, são N funcs, mas cada func está capacitado a fazer 2 destas tarefas. então 3 seria suficiente para executá-las todas, mas cada 2 tarefas apenas 1 está habilitado.
Este final é a restrição, se as tarefas são { A, B, C, D, E, F } vamos combinar aos pares para ver quantos funcionários serão necessários:
(A,B), (A,C),(A,D),(A,E),(A,F)
--------(B,C),(B,D),(B,E),(B,F)
_____ ____ (C,D), (C,E),(C,F)
_____ ____ ____ _(D,E),(D,F)
_____ ____ ____ _____, (E,F)
Percebe que (A,B) = (B,A) porque a ordem não importa basta que 2 executem 1 atividade.
Agora a parte teórica, você tem 6 atividadade, e a cada combinação 2 a 2 exige um funcionário
Exatamente o sentido dado por C(6,2)
Deu para entender ?
O problema não é qual o mínimo de funcionarios para as tarefas, mas quantos são necessários para que as funções não fiquem sem responsável.
[ ]s
-
Combinação de 6 tarefas tomadas de duas a duas (por funcionário): C 6,6 = 6! / 4!2! = 15
Ou pense em um relógio com 6 ponteiros: os números vizinhos fazem combinação, assim como o último e o primeiro (é um circulo), bem como podemos fazer uma ponte entre ponteiros não consecutivos fazendo novas duplas/combinações. O total dessas "ligações" é exatamente 15.
-
Se ficar com medo de usar combinação, é só fazer na munheca. Pense que a 6 tarefas são A, B, C, D, E e F. Logo, o funcionário só pode fazer as seguintes tarefas:
1 - A e B // 2- A e C // 3- A e D // 4- A e E // 5- A e F // 6- B e C // 7- B e D // 8- B e E // 9- B e F // 10- C e D // 11- C e E // 12 - C e F // 13 - D e E // 14- D e F // 15 E e F
-
Sinceramente nāo entendi o enunciado, nāo consegui visualizar a combinaçāo...
-
A pergunta que não quer calar, onde na questão que vocês concluíram que tratava-se de uma combinação?
-
Se tivesse opção f) com 3 funcionários eu ia marcar com certeza.
Vamos na fé.
-
Em um escritório há 6 tarefas básicas diferentes que devem ser cumpridas pelos funcionários: atender ao público, protocolar, arquivar, digitar, expedir documentos e fazer a manutenção dos computadores. Sabe‐se que cada funcionário do escritório está capacitado para executar exatamente duas dessas tarefas e, para cada duas tarefas, há um único funcionário capacitado a executá-las.
No escritório há 6 tarefas
Cada funcionário está capacidado para realizar 2 tarefas
De quantas formas possíveis cada funcionário pode realizar as tarefas?
Combine C(6,2) = 15 possibilidade de duas tarefas.
Cada funcionário pode executar quantas tarefas? extamente 2 tarefas!
Logo, precisa-se de 15 funcionários, porque cada funcionário executa apenas uma combinação de tarefa e há 15 combinações possiveis.
Se não viagei, deve ser isso!
-
Se existem 6 tarefas distintas, podemos combiná-las duas a duas de 15 maneiras, pois:
C(6,2) = 6 x 5 / 2 = 15
Assim, como para cada conjunto possível de 2 tarefas há um funcionário que é capaz de executá-las, são necessários 15 funcionários para cobrir todas as possibilidades de “duplas” de tarefas.
Resposta: C
-
GABARITO: C
Oi, pessoal. Vamos lá:
Vamos chamar as 6 atividades de A, B, C, D, E e F
Como cada funcionário só pode fazer duas dessas tarefas e só há um único funcionário que atende a uma combinação específica, podemos pensar assim:
O João pode executar as tarefas A e B e só há ele ali que as execute. Se ele executar, em vez de A e B, B e A, há alguma mudança? Não! Por esta razão, utilizamos combinação, pois a ordem não altera a tarefa: Lavar louça e arrumar a casa ou arrumar a casa e lavar louça são, em tese, a mesma coisa.
---
Porém, vamos pensar de outra forma:
→ Podemos ter, na tarefa A: AB, AC, AD , AE e AF
→ Na tarefa B, teremos: BC, BD, BE e BF.
→ Na tarefa C: CD, CE e CF
→ Na tarefa D: DE e DF
→ Na tarefa E: EF
Não teremos nada na tarefa F, pois todas as combinações com ela já foram feitas anteriormente.
Obs.: Lembrando que não existe "AA" nem "BB", pois você não lava a louça duas vezes. Nem podemos colocar BA e depois AB, pois é o mesmo funcionário que atende por elas.
Agora, quando contamos a quantidade de combinações que fizemos, haja vista que cada uma delas possui um funcionário responsável, encontramos a resposta: 15 funcionários.
Espero ter ajudado.
Bons estudos! :)
-
Resolvo essa questão aqui nesse vídeo
https://youtu.be/6xWCgG1OsCI
Ou procure por "Professor em Casa - Felipe Cardoso" no YouTube =D
-
Eu tenho 6 tarefas para agrupar em grupos de 2, onde dentro dos grupos não importa a ordem de cada tarefa. Portanto, usar combinação:
C(6,2)= (6*5)/2! = 15.
Letra C.
-
Questão super redundante, sem necessidade...
Sabe-se que cada funcionário do escritório está capacitado para executar exatamente duas dessas tarefas e, para cada duas tarefas, há um único funcionário capacitado a executá-las.
-
Minha lógica foi a seguinte:
1. Combinação das tarefas de duas em duas C(6,2) = 6.5/2.1 = 15 ;
2. Para cada dupla de tarefas, apenas um funcionário está capacitado a executar. Então para cada dupla de tarefas é necessário 1 funcionário;
3. 15 duplas de tarefas -> 15 funcionários diferentes.
-
Essa é uma questão de Combinação, onde a ordem não importa (se a questão se importar com a ordem será uma questão de arranjo)
C n/p = N!/ (N-P) P!
- Na questão ele quer a C(6,2)
Pra você não precisar usar a fórmula, basta fatorar o número de cima a mesma quantidade de vezes que o debaixo:
- 6,5/ 2,1= 15 ( GABARITO: C)
Espero ter ajudado!
-
Algum Concurseiro pq poderiamos ter outras opções como
funcionário 1: faz a,b
funcionário2: a,c
f3: b,c
f4: b,d
Veja que cada funcionário pode ter uma função em comum, mas não ambas.
-
C(6,2)
6*5/2*1
30/2
15
GAB C
-
Galera, pra quem não lembrar a fórmula "combinação de 6 tomados dois a dois", basta fazer na marra, porque o universo da questão é pequeno.
- Temos 6 tarefas, denominadas A,B,C,D,E,F
- Se, para cada duas tarefas há um único funcionário que pode executá-las é igual a questão do dominó, mas com menos números:
5 funcionários sabem fazer a tarefa A: AB, AC, AD, AE,AF
4 funcionários sabem fazer a tarefa B (exclui o AB, pq já foi contado no anterior), B: BC, BD, BE, BF
3 funcionários sabem fazer a tarefa C (exclui o AC e o BC, pq já foram contado nos anteriores) CD, CE, CF
2 funcionários sabem fazer a tarefa D (exclui o AD, o BD e o CD, pq já foram contado nos anteriores) DE, DF
1 funcionários sabe fazer a tarefa E (exclui o AE, o BE, o CE, eo DE pq já foram contado nos anteriores) EF
Todos os funcionários que sabem fazer F já foram contados nos anteriores pq cada funcionário sabe fazer 2 tarefas e p cada 2 tarefas só existe 1 funcionário.
5 + 4 + 3 + 2 + 1 = 15
GABARITO: C