-
Alguém sabe explicar essa?
-
Gabriela.
Sou novato no site e não sei se é possível inserir imagens neste espaço destinado a comentários.
Improvisei o desenho abaixo para ficar mais clara a resolução:
|....15.....|....15....|....15....|...9...|..1..|
. x
9 | | | x | |
. x
|....15.....|....15....|....15....| x |..1..|
. x
9 | | | | |
.
|....15.....|....15....|....15....|...9...|..1..|
.
2
........................................................
O comprimento de 55 é dividido em 3 comprimento menores de 15cm, sobrando duas partes, uma de 9cm e outra de 1cm.
A largura de 20 é dividido em 2 larguras menores de 9cm, restando uma parte de 2 cm.
Os números de retalhos retangulares de utilizando os 3 comprimentos menores de 15cm e 2 larguras menores de 9cm resultam em 3*2= 6.
O detalhe é que do comprimento 55 cm restou um parte de 9cm que é a largura do último retângulo. O comprimento deste retângulo é obtido cortando verticalmente ( a região onde tem os "x").
Portanto, o total de retangulos de 9 por 15 é 6+1= 7.
-
O pano mede 55 x 20
cada retalho deve ser de 15x9
55= 3x15 +10
20= 2x9 + 2 assim cabem 2 fileira de 15x9 sobrando um retalho final de 10 x 20 continuo, logo pode ser cortado mais 1: 2x3+1=7
GAB .A
-
Não entendi a resolução dessa questão! Alguém poderia me ajudar???
Obrigada!
-
O ideal era mostrar a resolução através de imagem, mas como o QC não disponibiliza mais esse recurso, vamos lá:
Não é difícil entender que pelo menos 6 retalhos de 15x9 cabem perfeitamente na peça de 55x20, certo? Eles ficarão agrupados em três colunas e duas linhas. A sacada vem agora: no restinho do espaço que sobra, é possível encaixar mais um retalho se o rotacionarmos 90º. Nesse caso teremos o total de 7.
Recomendo fazer o desenho no Power Point ou Impress com as medidas exatas para entender bem a questão.
-
esta questão nunca poderia ter a resposta como 7...deveria ser 8 pq a resolução é bem fácil....como a questão pede o número máximo de retalhos então e só dividir a área total do pano maior A=55x20=1100cm2 por A=15x9=135cm2 pano menor...dando 8,1481 retalhos, como não se pode aproveitar pedaços menores como a questão diz, desprezamos o resto 0,1481....entao teremos 8 retalhos...podemos fazer uma bandeira com quatro colunas e duas linhas como mostro abaixo....(nao deu pra colocar as linhas unidas)
oooo
oooo
-
@Carlos, é que não se pode juntar os retalhos. Por mais que vc tenha área disponível... não cabe o retângulo que ela quer cortar. Desenhe ae no seu caderno que entenderá.
-
Eu fiz o desenho do quadrado e em 55 cabem 3 retalhos de 15 cm em 20 cabem 2 de 9cm
Como é dentro de uma área multipliquei e tem um retlaho sobrando conforme o problema fala
3 x 2=6 +1 =7
-
Estou com duvidas ,olhem isso na questao:considerando que um retalho nao podera ser feito costurando 2 pedacos menores.por isso errei a questao marquei 6 pedaços,pois nao pode costurar pedaços menores.alguem pode ajudar?
-
Questão resolvida pelo professor Joselias...
http://www.youtube.com/watch?v=KPy307USD4A
Bons estudos...
-
Problema dessa questão que ela precisa de régua e desenho, senão n tem como fazer, nesse concurso pode-se usar régua?
-
Não precisa de régua. é só você imagina um tecido de 55cm X 20cm, você conseguiria 6 pedaço dentre 45cmX 20cm, sobraria mais um pedaço de 10cm X 20cm que daria mais um pedaço. seria possível 7 pedaços.
BONS ESTUDOS!
-
Fui seco na resposta de 6 retalhos, mas depois percebi que realmente são 7. :P
-
Considerando
que um retalho não poderá ser feito costurando dois pedaços menores, não
podemos dividir a área do maior retângulo pelo menor.
Resolvendo através do desenho
abaixo:
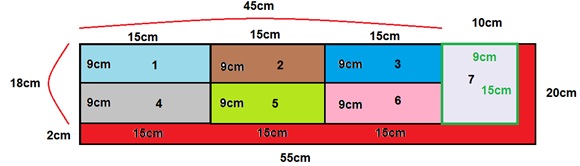
RESPOSTA: (A)
-
Que falta de criatividade desse examinador! O que agrega fazer uma questão como essa?
-
Fiz a questão calculando a área total e dividindo pela área dos retângulos menores. Acertei. Fiquei surpreso ao ver as estatísticas.
-
https://youtu.be/Z5_qUkEXe8o
-
A chave para resolver é este trecho do enunciado: "Considerando que um retalho não poderá ser feito costurando dois pedaços menores...". Pois se pudesse costurar com pedaços menores, a resposta seria 8.
-
Vejam o desenho que fica mais fácil de entender. No vídeo do Ivan Chagas está muito bem explicado.
https://youtu.be/Z5_qUkEXe8o
Bons estudos!