-
Se é verdade que alguns adultos são felizes e que nenhum aluno de matemática é feliz, então é necessariamente verdade que:
-
por que não a letra A? No grupo dos adultos que não são felizes, pode ter algum que é aluno de matemática.
-
catia
“por que não a letra A? No grupo dos adultos que não são felizes, pode ter algum que é aluno de matemática.”
A pergunta da questão é“necessariamente verdade” equivale a “obrigatoriamente” ou “certeza absoluta” .
Tem que se limitar às informações fornecidas.
Não há nada afirmando que alguns adultos não são felizes.
Veja um exemplo para ficar mais claro.
Se num grupo de adultos X formado por Ana, Beto,Caio, Daniel e Eric, digo “Ana e Beto são felizes” infere-se que os outros são infelizes?
Não. Eu não posso afirmar isso. Pode ser que entre os outros três haja mais alguém que seja também feliz.
Tudo que sei é que afirmei apenas referente a alguns deles (Ana e Beto).
Como você mesmo colocou “PODE”. É uma possibilidade, mas não uma certeza.
Os outros (Caio, Daniel e Eric) tanto pode ser felizes como infelizes. Certeza mesmo é que não tenho elementos suficientes para ter uma conclusão sobre eles.
-
Mas se nenhum aluno de matemática é feliz, e os adultos são, logo nenhum aluno de matemática é adulto.
-
Mas se nenhum aluno de matemática é feliz, e os adultos são, logo nenhum aluno de matemática é adulto.
Temos de levar em consideração apenas o que está no texto, do jeito que aparece, sem suposições. Sendo assim, a única alternativa cabível é a c, pois leva em consideração que ALGUNS adultos são felizes, ou seja, aquele que é feliz não é aluno de matemática.
-
Questão simples, pois se "alguns adultos são felizes e que nenhum aluno de matemática é feliz", então é o mesmo que dizer que "algum adulto não é aluno de matemática", já que alguns adultos são felizes e não todos. Logo, essa parcela que é feliz não pode ser estudante de matemática.
Letra C.
-
problema desta questão que muita gente confundiu o enunciado com a parte de negação da logica, inclusive eu... :(
lembrando que algum = nenhum; nenhum = algum ; todo = algum,..nao ; e , algum , ... nao= todo
-
O ADULTO QUE É FELIZ NÃO É ALUNO DE MATEMÁTICA, OU SEJA, ''algum adulto não é aluno de matemática''
POR QUE???
PORQUE NENHUM ALUNO DE MATEMÁTICA É FELIZ!
GABARITO ''C''
-
Perceber que as alternativas A e D são equivalentes, já que afirmar que ALGUM A É B equivale a afirmar que ALGUM B É A. Logo, não poderia ser nenhuma das duas alternativas.
Da mesma forma, as alternativas B e E, pois afirmar que NENHUM A É B equivale a afirmar que NENHUM B É A.
Com essa lógica pode-se resolver a questão sem precisar ler o enunciado.
Espero ter ajudado!
-
Podemos resolver a questão fazendo uso do diagrama de Venn. Por exemplo imaginemos dois conjuntos A e F que representem respectivamente o conjunto dos Adultos e dos Felizes e um outro conjunto M que represente o dos alunos de matemática. Como não existe aluno de matemática feliz então M e F são disjuntos, por outro lado existe adulto feliz então a única afirmação que é necessariamente verdade é que algum adulto (os adultos e felizes simultaneamente) não é aluno de matemática, obviamente porque M e F são disjuntos.
-
A única afirmação que pode ser feita é a de que algum adulto não é aluno de matemática, afinal ele é feliz. (letra C).
Mesmo que seja possível inferir a informação de que alguns adultos não são felizes, não é possível afirmar que estes sejam necessariamente alunos de matemática. (o que excluí as alternativas A e D, que podem gerar alguma dúvida).
-
Segundo BIZU do professor Renato Oliveira aqui do Qconcursos para responder questões em que só apareçem ALGUM e NENHUM, usa-se a eliminação das sentenças iguais, onde as idéias estão invertidas, mas o sentido é o mesmo, conforme abaixo:
a) algum adulto é aluno de matemática. ( essa afirmativa é igual a afirmativa da letra D, só foi invertida a construção da frase, por isso elimina-se a letra D)
b) nenhum adulto é aluno de matemática. (essa afirmativa é igual a letra E, só foi invertida a construção da frase, por isso elimina-se a letra E)
c) algum adulto não é aluno de matemática. (Sentença VERDADEIRA)
d) algum aluno de matemática é adulto. (eliminada pela letra A)
e) nenhum aluno de matemática é adulto. ( eliminada pela letra B)
Logo por eliminação encontrou-se a letra C como sentença verdadeira.
-
Eu usei conjuntos
fiz dois conjuntos...um de adultos e um de felizes. Como uns adultos sao felizes, tem uma intersseção entre eles.
Ae fiz um conjunto de matematico. Só que o conjunto matematico pode estar dentro do conjunto adulto sem ser da interceção ou fora dos conjuntos.
Entao procurei umaalternativa q era plausivel pra os dois casos.
-
Podemos montar o seguinte diagrama, no qual marquei com 1 e 2 duas áreas que devemos avaliar:
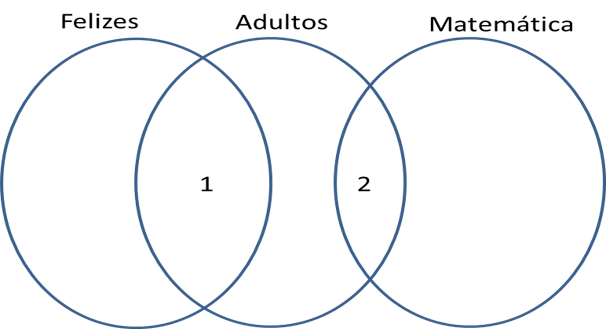
Como alguns adultos são felizes, certamente existem elementos na região 1. E como nenhum aluno de matemática é feliz, então os conjuntos “felizes” e “matemática” não possuem intersecção. Avaliando as alternativas:
a) algum adulto é aluno de matemática. → ERRADO. Não temos elementos para afirmar que a região 2 possui elementos.
b) nenhum adulto é aluno de matemática. → ERRADO. Também não temos elementos para afirmar que a região 2 é vazia.
c) algum adulto não é aluno de matemática. → CORRETO. Os adultos que são felizes estão na região 1, e assim automaticamente não fazem parte do conjunto dos alunos de matemática.
d) algum aluno de matemática é adulto. → ERRADO. Não temos informações para afirmar que existe algum elemento na região 2.
e) nenhum aluno de matemática é adulto. → ERRADO. Não temos informações para afirmar que a região 2 está vazia.
Resposta: C
-
Fala galera... No Canal Matemática com Morgado vocês encontram a resolução completa dessa questão, e de brinde um resumão sobre diagramas lógicos !!! Bom estudo a todos :)
https://youtu.be/2_ktJa0AIyE
-
tentem por conjuntos , acho que e mais fácil
-
GABARITO LETRA C.
Eu geralmente resolvo essas questões por diagrama, porém quando tem Algum e Nenhum faço dessa forma:
Alguns adultos são felizes (sentença 1)
Nenhum aluno de matemática é feliz (sentença 2)
1º Cortar a parte incomum entre as sentenças (Feliz)
Alguns adultos são felizes (sentença 1)
Nenhum aluno de matemática é feliz (sentença 2)
2º Entre Algum e Nenhum prevalece o Algum + NÃO (acrescentar o Não)
Alguns adultos NÃO
3º Por fim, acrescentar o restante da sentença do Nenhum.
Alguns adultos NÃO são alunos de matemática = Algum adulto não é aluno de matemática