-
A questão sem colocar palpite no meio seria...
58 (total) - 18 (elementos que estão na interseção)= 40
Agora pega valor de só A + só B + só C=40
B-1+ B + 5+B =40
3B=36
B=12
Logo= C= 5+B= 17
-
A e B = 13
A e C = 3
B e C = 2
A e B e C = 0
TOTAL = 18 números em comum com dois grupos ou mais
C = B + 5
A = B -1
Números exclusivos de um só grupo( A + B + C )= 58 -18 = 40
Substituindo:
(B - 1) + B + (B + 5) = 40
3B = 36
B = 12
C = B + 5 = 17
-
Vaos lá:
Uma maneira mais facil!
a=x-1
b=x
c=x+5
Agora faz a equação:
x-1+x+x+5+3+2+13=58
3x+22=58
3x=36
x=12
Mas a pergunta diz "O número de elementos que pertencem apenas ao conjunto C é igual a:"
Pega a formula do c
c=x+5
c=12+5
c=17
Resposta=d
-
Resolvendo pelo diagrama de Venn:
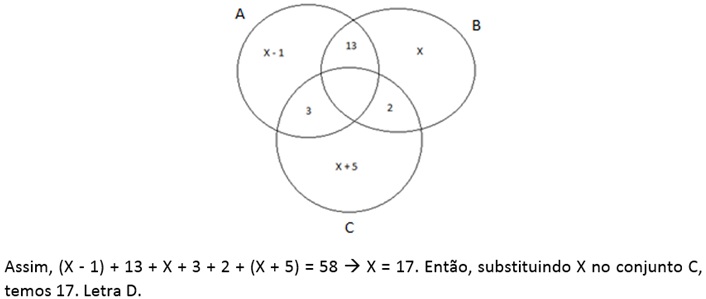
-
Gabarito. D.
O legal [e fazer o diagrama !
A e B = 13
B e C = 2
A e C = 3
Se ligar nos dados da quest'ao C = B + 5 unidades
A = B -1
Ao todo temos 58 elementos
58-18 que e a soma = 40
logo basta calcular B
B+-1+ B+5 + B =40
3B = 40-4
B = 36/3 = 12
Achamos B logo [e s[o calcular
A = B-1 = 11
C = B+ 5 = 17
-
B=X(não sei quem é B, portanto vou considerá-lo como X)
A= X-1( o número de elementos que pertencem apenas ao conjunto A é 1 unidade a menos do que aqueles que pertencem apenas ao conjunto B)
C= X+5( o número de elementos que pertencem apenas ao conjunto C é 5 unidades a mais do que aqueles que pertencem apenas ao conjunto B)
Agora é só somar todos os dados dos conjuntos e igualar a 58 que é o total de elementos, ou seja, A+B+C=58. Ficará:
x-1+13+x+3+2+x+5=58
3x + 22=58
3x=36
x=12.
Pronto, já descobrimos o valor de X, agora é só substituir de acordo com a questão. Assim:
B= 12
A= 12-1=13
C= 12+5=17 (NOSSA RESPOSTA)
-
Bel, obrigada pelo comentário... do jeito que o professor do QC explicou fiquei com dúvidas quanto à resolução do x dentro dos parênteses..
-
melhor q a do professor sua explicação....valeu
-
Eu quebrei a cabeça. Mas achei, pela equação do 1° grau, uma forma bem simples de fazer. Do mesmo modo que a colega havia anunciado no comentário anterior.
-
soma todo o valor que se tem e diminui pelo total,depois divida por 3 kk
-
Para quem fez o diagrama e completou, assim fica fácil:
B-1+B+5=58 => 2B=54 => B=54/2 => B=27
Nas intercecções com B, basta achar o valor apenas de B. Então: 27-13-2=12.
Achando o valor de B, tem-se o valor de C, no qual: C=B+5 => C=12+5 => C=17
Espero ter ajudado =)
-
questão tranquila, só fiquei "cabreiro" com o termo "APENAS"(apenas ao conjunto C... ao A... Ao B). Mas, não era pegadinha.
-
Explicação do PS Machado foi ótima!
-
Gabarito: D
-
A+B+C = 58
C = B+5
A = B-1
Substituindo:
B-1 + B + B+5 = 58
3B + 4 = 58
3B = 58 - 4
3B = 54
B = 54/3
B = 18
A questão quer saber a quantidade de elementos que pertencem apenas a C.
Se C = 5 + B e B =17
C = 5 + 17
C = 23
Mas 23 é a quantidade total de C.
Sabendo que A e C "dividem" 3 elementos e B e C "dividem" 2 elementos, precisamos retirar esses elementos.
Logo, 23 - 5 = 17.
-
Esta questão deveria ter sido anulada, pois o enunciado menciona "que o número de elementos que pertencem APENAS ao conjunto C..."; "APENAS ao conjunto A"; "APENAS ao conjunto B", ou seja, não contempla as intersecções AB, BC, CA. Desta forma, a resolução correta seria:
A + B + C = 58, sendo:
A = x-1+13+3
B = x+13+2
C = x+5+3+2
Logo: (x-1+13+3) + (x+13+2) + (x+5+3+2) = 58
3x = 58-40
x = 18/3 = 6
Resp: Pertencem APENAS ao conjunto C = 11 (x+5)
PS: partindo da lógica que desconsidera o APENAS, o gabarito é C=17, portanto A=11 e B=12. Ora, A+B+C=58, contudo, 11+12+17=40 !!!
* * * QUESTÃO ERRADA * * *
-
SÃO 58 ELEMENTOS
interseção AB --> 13
interseção AC --> 3
interseção BC --> 2
Faltam 40 elementos.
Resolvi tentando todas as alternativas.
Pertence apenas ao conjunto C --> 17
Pertence apenas ao conjunto B --> 12
Pertence apenas ao conjunta A --> 11