-
Vamos
fazer as contas pra quem deu primeiramente 28 passos para a direita. Temos uma
PA de razão 2, onde nosso a1 = e n = 28, vamos encontrar o n e logo depois
vamos calcular a soma dessa PA, assim:
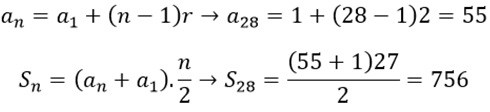
Fazendo o mesmo procedimento para quem deu 27 passos para a esquerda, onde a razão também é 2, mas o a1 = 1 e o an = 27, logo:
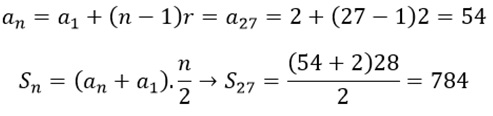
Fazendo 784 - 756 encontraremos 28.
Letra C.
-
Fiz depois de muuuuito Raciocínio MESMO:
Passos a Direita: 3 passos = 1+3+5 = 9 --> 3^2 = 9; 5 passos = 25 --> 5^2 = 25. Ou seja, são resultados de exponenciação "ao quadrado". Logo 28 passos: 28^2 = 784 Passos a Esquerda: 3 passos = 2+4+6 = 12 --> 3 * 4 = 12; 4 passos = 20 --> 4 * 5 = 20. Ou seja, os valores dos passos é uma multiplicação do passo por ele mesmo mais um [n*(n+1)]. Logo, 27 passos: 27*28 = 756. Direita - Esquerda : 784 - 756 = 28.
-
A lógica da formação da soma de quem dá passos para a direita é de "n²", onde "n" é o número de passos para direita.
Já a lógica da formação da soma de quem dá passos para a esqueda é de "n²+n", onde "n" é o número de passos para esquerda.
Assim, 28 passos para a direita resulta em 28² = 784, enquanto 27 passos para a esquerda resulta em 27²+27 = 756.
Então 784-756 = 28, resposta "c".
-
putz, alguém tem uma explicação mais simples?
-
Não é necessário calcular o valor total das sequências para resolver esse problema. Basta descobrir a lógica. Vejamos:
2 passos D - 1 passo E: (1 + 3) - 2 = 4 - 2 = 2
3 passos D - 1 passo E: (1 + 3 + 5) - (2 + 4) = 9 - 6 = 3
Por aí já se verifica que a diferença entre a soma do lado direito (n passos) e a soma do lado esquerdo (n - 1 passos) é numericamente igual ao número de passos do lado direito. Então, se foram dados 28 passos para a direita, a resposta é 28.
-
1 - Descobrir qual o 28 termo da direita com a fórmula da P.A = 55.
2- Descobrir o 27 termo da esquerda com a fórmula da P.A = 54.
3 - Fórmula das somas dos termos da P.A. da esquerda (=756) e da direita (=784).
4 - Subtrair os valores = 28.
-
Simples, é fácil ver que, para a direita nxn = soma e para a esquerda nx(n+1) = soma. n é o número de passos!
-
Galera, existe sim um jeito mais simples de resolver esta questão. Vamos lá:
1) Calculando os passos à esquerda:
Perceba de uma maneira prática que se somarmos os n primeiros números pares positivos teremos:
n = 2 → 2 + 4 = 6 = 2 x 3;
n = 3 → 2 + 4 + 6 = 12 = 3 x 4;
n = 4 → 2 + 4 + 6 + 8 = 20 = 4 x 5; e por aí vai... ou seja, em se tratando dos primeiros números pares, basta pegar a quantidade que vc quer e multiplicar pelo posterior, ficando desta forma; n ( n + 1). Nesta questão, como são 27 passos, temos:
27 x 28 = 756
2) Calculando os passos à direita:
Perceba de uma maneira prática que se somarmos os n primeiros números ímpares positivos teremos:
n = 2 → 1 + 3 = 5 = 2 x 2; n = 3 → 1 + 3 + 5 = 9 = 3 x 3;
n = 4 → 1 + 3 + 5 + 7 = 16 = 4 x 4; e por aí vai... ou seja, em se tratando dos primeiros números ímpares, basta pegar a quantidade que vc quer e elevar ao quadrado, ficando desta forma; n x n. Nesta questão, como são 28 passos, temos:
28 x 28 = 784
Portanto, a diferença pedida é 784 – 756 = 28.
Conheçam e inscrevam-se no meu canal no youtube, pois sou professor de Matemática e gravei alguns vídeos com dicas e bizus de Matemática e Raciocínio Lógico.
Link do canal: https://www.youtube.com/channel/UC_FQm8aivYBf2q6ga1rxklw
Face: JULIO CESAR SALUSTINO
-
Fiz as duas somas.
28 passos para a direita = 784
27 passos para a esquerda = 756
784-756= 28
Letra: "c".
Boa sorte e bons estudos!
-
O número de passos para direita será ele * ele mesmo. O número de passos para a esquerda será ele*seu consecutivo.
Ex.
Passos para direita: p.2*2=4 (1+3) ; p.3*3=9 (1+3+5=9).
Passos para esquerda: p.2*3=6 (2+4=6); p.3*4=12 (2+4+6=12).
28 passos para direita*28= 784
27 passos para esquerda*28= 756
784-756= 28.
-
Alguém tem a resolução desta questão em vídeo?