-
Medida 1: Terreno quadrado de lado (x) assim temos (área 1) = x^2.
Medida 2: 2 lados com (x) e outros 2 com (x-0,2) assim temos (área 2) = x * (x-0,2)
Além disso é dito que:
(área 2) = (39/40) * (área 1)
x * (x-0,2) = (39/40) * x^2 ==> 40x^2 - 8x - 39x^2 = 0
x^2 - 8x = 0 ==> x = 0 m ou x = 8 m.
Se tratando de tamanho de terrenos usaremos x = 8 m.
Perímetro para a segunda medição.
2 * ((x - 0,2) + x) = 2 * 15,8 = 31,6 m.
-
A área antiga é a área A do quadrado x² e a nova área seria a área A' do retângulo (x-20). x, assim:
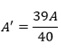
Substituindo-se os valores:
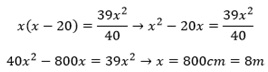
O perímetro é a soma de todos os lados, assim:
P = 8 + 8 +(8 - 0,2) + (8 - 0,2) = 31,6m
Letra B
-
Valdivan, como chegou a conclusão de que x = 0 ou 8 metros? Parei quando cheguei em X² - 8 X = 0.
-
Tb não entendi!!
=/
-
Como o resultado está em metros, devemos converter 20 cm em 0,2 metros.
área do retângulo é: x (x-0,2). esta área é 39/40 da área supostamente quadrada x^2.
Logo: x(x-0,2)=(39/40)x^2
ou x^2-0,2x=39/40 x^2
Passando só o 40 cruzando para a esquerda e multiplicando temos:
40 x^2 - 8 x = 39 x^2
logo: x^2 - 8 x = 0
-
Alguém pra explicar com detalhes ? se cai uma dessa na minha prova eu choro kkkkkk
-
Socorro!!! não entendi nada.
-
Quando chegar em 40x² - 8= 39x², posso cancelar o ² certo???
-
O quadrado tem os 4 lados (L) iguais, então sua área é : Aq = L², o perímetro é a soma dos lados: P=4L.
O retângulo tem base e altura diferente, então: Ar = base x altura = bxh, já o perímetro : P=2x (b+h).
Bom, a questão nos diz que a área do quadrado é x por x: Aq = x²,
e a área do retângulo é x por x por x-20 cm por x-20 com, ou seja Ar=x(x-20).
Nos diz tbm que a área do retângulo é 39/40 da do quadrado : Ar = 39/40 de x² .
Agora é só juntar as informações e resolver conforme o professor.
-
Boa Noite!
Nessa questão, não será necessário trabalhar com equação do segundo grau. Vejamos a solução:
1) Inicialmente o agrimensor acreditou que tratava-se de um terreno no formato de um quadrado, isto é, uma figura geométrica de quatro lados iguais, na qual a área é o lado elevado ao quadrado, chamando o lado do quadrado de X, temos: área = X²
2) Numa outra abordagem o agrimensor verificou que se tratava de um terreno retangular, o qual possuia dois lados iguaia a X e os outros dois iguais X - 20, pois tinham 20cm a menos que o lado do quadrado. Desta forma a área do retângulo será: X.(X-20) a nova área equivale 39/40 da área do quadrado. Montando a equação, temos:
X.(X-20) = 39.X²/40
X² - 20X = 39.X²/40
40. (X² - 20X) = 39X²
40X² - 800X = 39X²
X² - 800X = 0
X(X - 800) = 0
X = 800 ou X = 0 (descarta)
Nas dimensões do retângulo, que é a medida certa,temos: X, X, X-20 e X-20, ou seja, 800, 800, 780 e 780. Como o perímetro é a soma de todos os ladoa, tem-se que:Perimetro = 800 +800 +780 + 780 = 3160 cm. Transformando para metros, temos 31,60m = 31,6m
Resposta: "b"
Fiquem na paz!
-
Que questão complicada, não entendi
-
Fiz de maneira diferente dos colegas, mas encontrei o mesmo resultado:
Trata-se de um retângulo com dois lados "x" e dois lados "x-20cm". Convertendo "20cm" para metro temos "0,2m", valor esse que usei para montar a seguinte fórmula:
x+(x-0,2)+x+(x-0,2).
Resolvendo: 4x-0,4 => x=0,4/4 => x=0,1
A área do terreno é "39/40". Somando o numerador (39) com o denominador (40), obtemos "79". Agora basta multiplicarmos 79, pelo número de lados da figura (4) e em seguida pelo valor de x (0,1). Assim:
79*4*0,1= 31,6
Resposta: 31,6m
-
O meu maior problema é na hora de por cada termo no seu lugar, por exemplo:
"Com isso, a área correta do terreno é de 39/40 da área inicialmente suposta"
Aí eu sempre me confundo na hora de montar o cálculo, aí eu faço isso:
X.(X-20).39/40 = X² ao invés disso X.(X-20) = 39.X²/40
algm tem alguma dica pra eu parar com essas confusões?
-
Questão tranquila, basta atentar para "39/40 DA área inicialmente suposta", portanto:
Área inicialmente suposta = x² (área de um quadrado)
Nova área = 39/40*x²
Área do retângulo = x²-20x
Basta resolver a equação -> x²-20x=39/40x² -> x=800 cm ou 8m
Perímetro = 8+(8-0,2)+8+(8-0,2)=31,6 -> LETRA B
-
X-800x=0 x(800-x)=0 x=800 perímetro do retângulo=2×800+2×780=3160cm logo: 31,6m
-
um jeito bem mais facil q eu achei de fazer
se a nova é 39 de 40 da outra q achava ser, entao:
esses 20 * 40 daria 800 que é total de X em centimetros e
20 * 39 = 780 centimetros, que seria o lado x-20.
780+780+800+800 = 3120 centimetos
3160/100 = 31,60 metros
-
Alguém me ajuda a encontrar o erro do meu raciocínio? Se 0,20 cm + 0,20 cm somados a 31,60 m - ou melhor, 3,160 cm - resultam em 3.200 cm, então esse seria a área equivocadamente considerada, certo? 39/40 disso seria a área correta, certo? Se eu dividir por 40 e multiplicar por 39 não vai dar 31,6. Onde estou errando? Grato.
-
Área do suposto terreno ( quadrado) = x^2
Área retângulo = 39/40* x^2
Sendo assim:
x*(x-20)= 39/40* x^2
X^2-20x= 39/40* x^2
passa o 40 multiplicando
40*(X^2- 20x)= 39x^2
40x^2 - 800x= 39x^2
x^2-800x=0 ( caimos numa equação incompleta de 2° grau)
colocando o x em evidência:
x* (x-800)= 0
X=0 ou
X-800=0
X=800
Voltando ao retângulo ( perímetro):
x+x+x-20+x-20, ou seja, 800+800+780+780
Perimetro = 3.160 CENTÍMETROS, passando para metros = 31,60m ( alternativa B)